Anhang D: Der Transformer illustriert (von Jay Alammar)
Dies ist die deutsche Übersetzung des exzellenten Blog-Artikels The Illustrated Transformer von Jay Alammar (2018). Alle Illustrationen stammen von Jay Alammar. Für diese Übersetzung (und alle Übersetzungsfehler) ist Michael Kipp verantwortlich. Dieser Beitrag ist, ebenso wie der Originalartikel, unter der Creative-Commons-Lizenz CC BY-NC-SA 4.0 lizensiert.

In diesem Artikel werden wir uns den Transformer ansehen - ein Modell, das Aufmerksamkeit (Attention) nutzt, damit das Training solcher Modelle mit hoher Geschwindigkeit durchgeführt werden kann. Der Transformer schlägt das Modell des Google Neural Machine Translation inhaltlich in bestimmten Aufgaben. Der größte Vorteil liegt aber darin, dass sich der Transformer zur Parallelisierung eignet. Tatsächlich empfiehlt Google Cloud die Verwendung des Transformers als Referenzmodell für ihr Cloud-TPU-Angebot. Also lasst uns dieses Modell unter die Lupe zu nehmen und verstehen, wie es funktioniert.
Der Transformer wurde in dem Paper Attention is All You Need vorgestellt. Eine TensorFlow-Implementierung davon ist als Teil des Tensor2Tensor-Pakets verfügbar. Die NLP-Gruppe der Harvard-Universität hat einen Leitfaden erstellt, wo das genannte Paper mit einer PyTorch-Implementierung annotiert ist. In diesem Artikel werden wir versuchen, alles möglichst einfach darzustellen und die Konzepte Schritt für Schritt zu erläutern, um es hoffentlich auch für Menschen ohne Spezialkenntnisse verständlich zu machen.
D.1 Überblick und Eingabe
Wir betrachten das gesamte Modell erstmal als Blackbox. In der maschinellen Übersetzung würde das Modell einen Satz in der Ausgangssprache als Eingabe bekommen und die Übersetzung des Satzes in die Zielsprache ausgeben.

Wenn wir in diesen “Optimus Prime” hineinschauen, sehen wir eine Kodierungskomponente (Encoder), eine Dekodierungskomponente (Decoder) und Verbindungen zwischen ihnen.
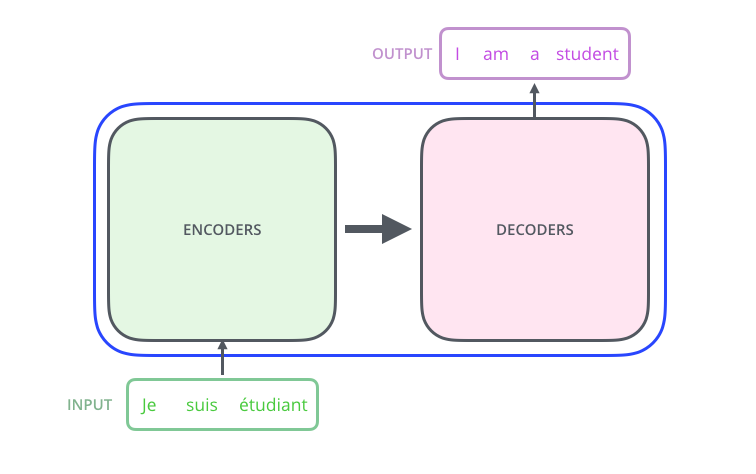
Die Kodierungskomponente besteht aus einer Reihe von Encodern (im Paper werden sechs von ihnen übereinander gestapelt - die Zahl sechs ist nicht magisch, es kann definitiv mit anderen Anordnungen experimentiert werden). Die Dekodierungskomponente besteht aus einer Reihe von Decodern derselben Anzahl.
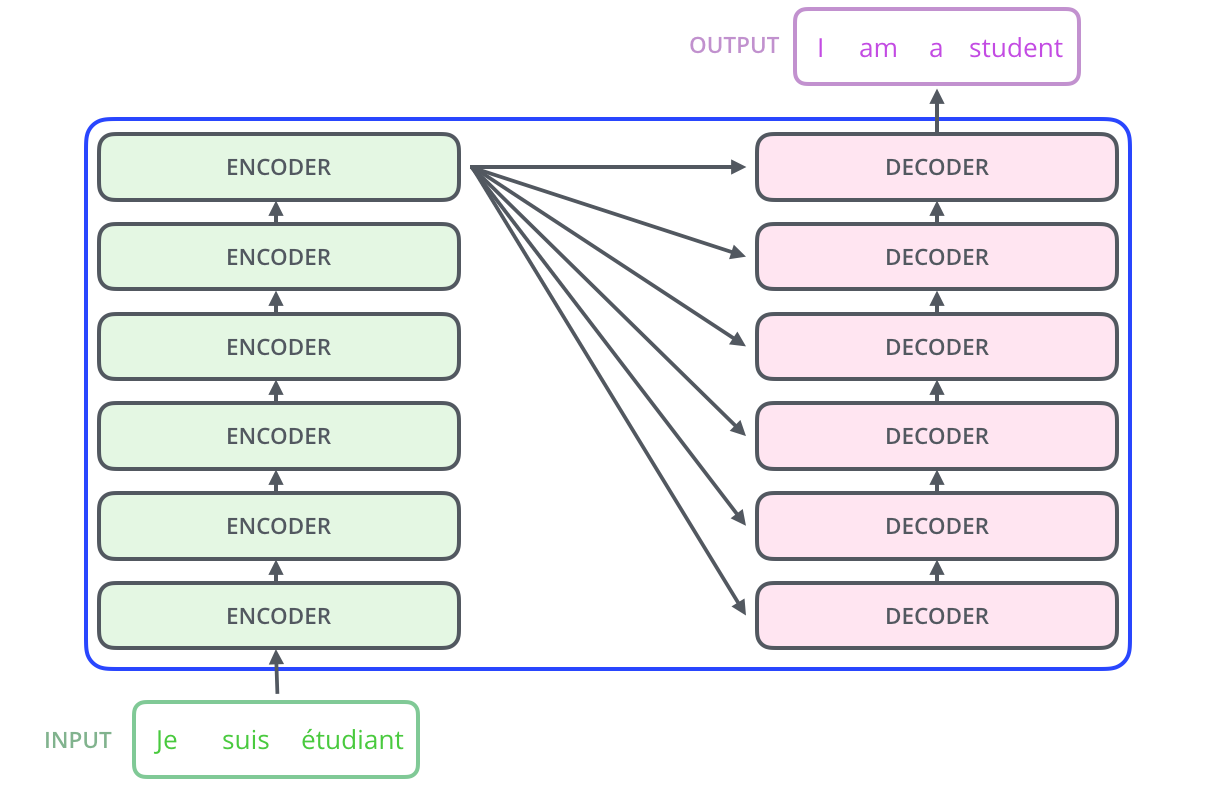
Die Encoder sind alle in ihrer Struktur identisch (aber sie teilen keine Gewichte). Jeder ist in zwei weitere Schichten unterteilt:
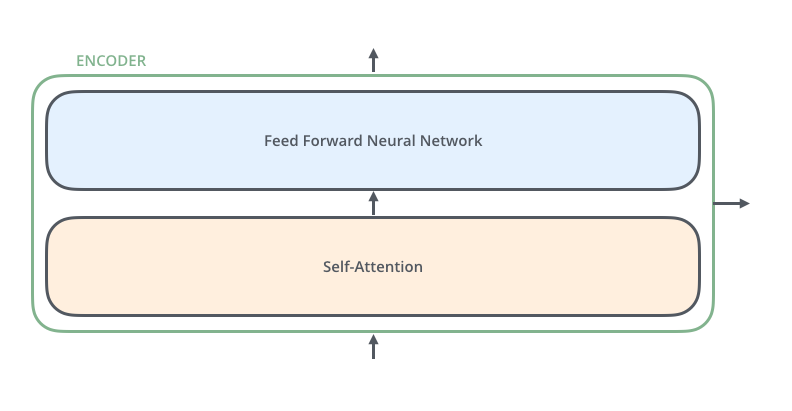
Die Eingaben des Encoders durchlaufen zunächst eine Self-Attention-Schicht - eine Schicht, die dem Encoder hilft, sich andere Wörter im Eingabesatz anzusehen, während er ein bestimmtes Wort codiert. Wir werden uns später genauer mit Self-Attention beschäftigen.
Die Ausgaben der Self-Attention-Schicht werden einem Feedforward-Netz zugeführt. Dieses Feedforward-Netz wird auf jedes einzelne Wort angewendet.
Der Decoder hat auch diese beiden Schichten, aber dazwischen befindet sich eine Attention-Schicht, die dem Decoder hilft, sich auf relevante Teile des Eingabesatzes zu konzentrieren (ähnlich wie bei der Attention in Seq2Seq-Modellen).
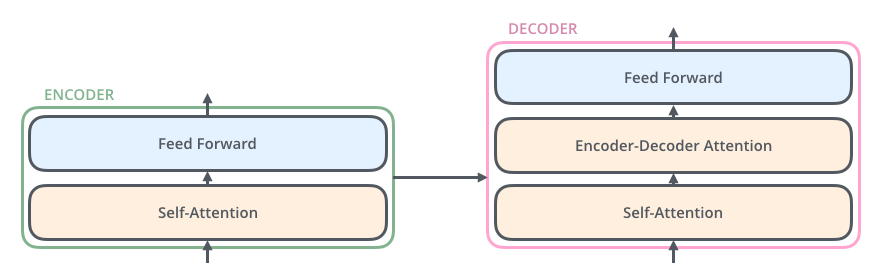
D.1.1 Jetzt kommen Tensoren
Nachdem wir die Hauptkomponenten des Modells gesehen haben, werfen wir nun einen Blick auf die verschiedenen Vektoren/Tensoren und wie sie zwischen diesen Komponenten fließen, um die Eingabe eines trainierten Modells in eine Ausgabe umzuwandeln.
Wie allgemein üblich in NLP-Anwendungen wandeln wir zunächst jedes Eingabewort mithilfe eines Embedding-Verfahrens in einen Vektor um.

Die Umwandlung in Word Embeddings erfolgt nur im ersten Encoder. Die Gemeinsamkeit aller Encoder besteht darin, dass sie eine Liste von Vektoren erhalten, die jeweils Länge 512 haben. Im ersten Encoder handelt es sich dabei um die Word Embeddings, aber in den weiteren Encodern handelt es sich um die Ausgabe des vorgeschalteten Encoders. Die Größe dieser Liste ist ein Hyperparameter, den wir festlegen können - normalerweise die Länge des längsten Satzes im Trainingsdatensatz.
Nach der Berechnung der Word Embeddings in der Eingabesequenz passiert jede Embedding die zwei Schichten des ersten Encoders.
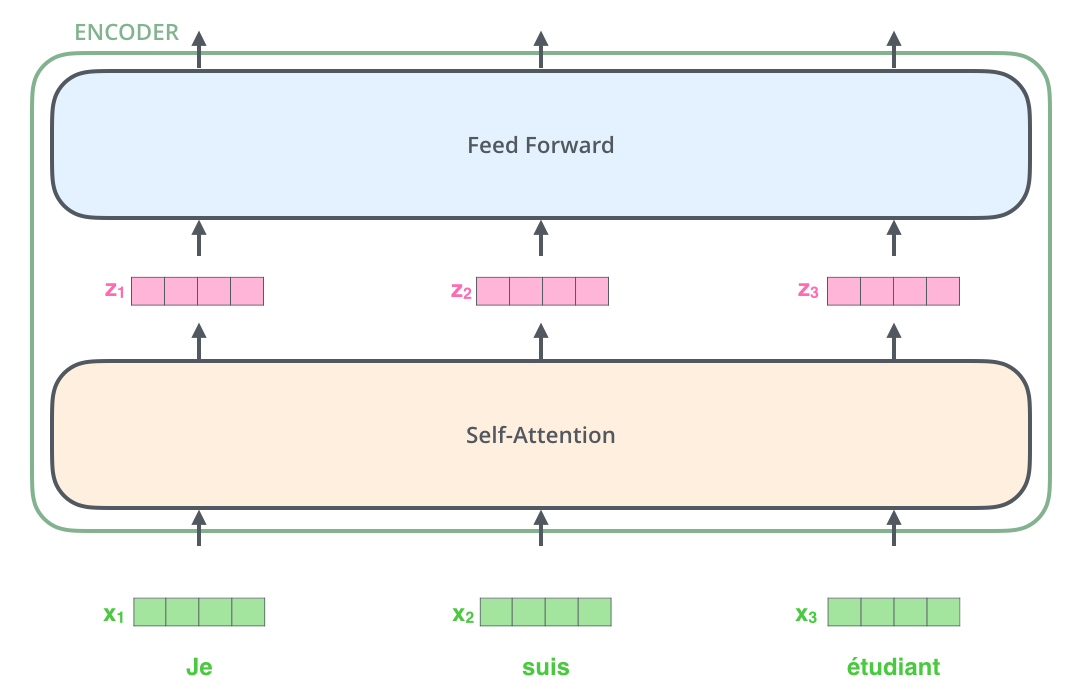
Hier beginnen wir, eine wichtige Eigenschaft des Transformers zu erkennen: Jedes Wort durchläuft seinen eigenen Pfad im Encoder. In der Self-Attention-Schicht gibt es Interaktionen zwischen diesen Pfaden. Aber die Feedforward-Schicht hat keine solchen Abhängigkeiten, und daher können dort die verschiedenen Pfade parallel ausgeführt werden.
Als nächstes werden wir uns als Beispiel einen ganz kurzen Satz vornehmen und schauen, was in jeder Schicht des Encoders passiert.

D.1.2 Jetzt wird enkodiert!
Wie bereits erwähnt, erhält ein Encoder eine Liste von Vektoren als Eingabe. Er verarbeitet diese Liste, indem er diese Vektoren in eine Self-Attention-Schicht gibt, dann in ein Feedforward-Netz, und dann die Ausgabe an den nächsten Encoder weiterleitet.
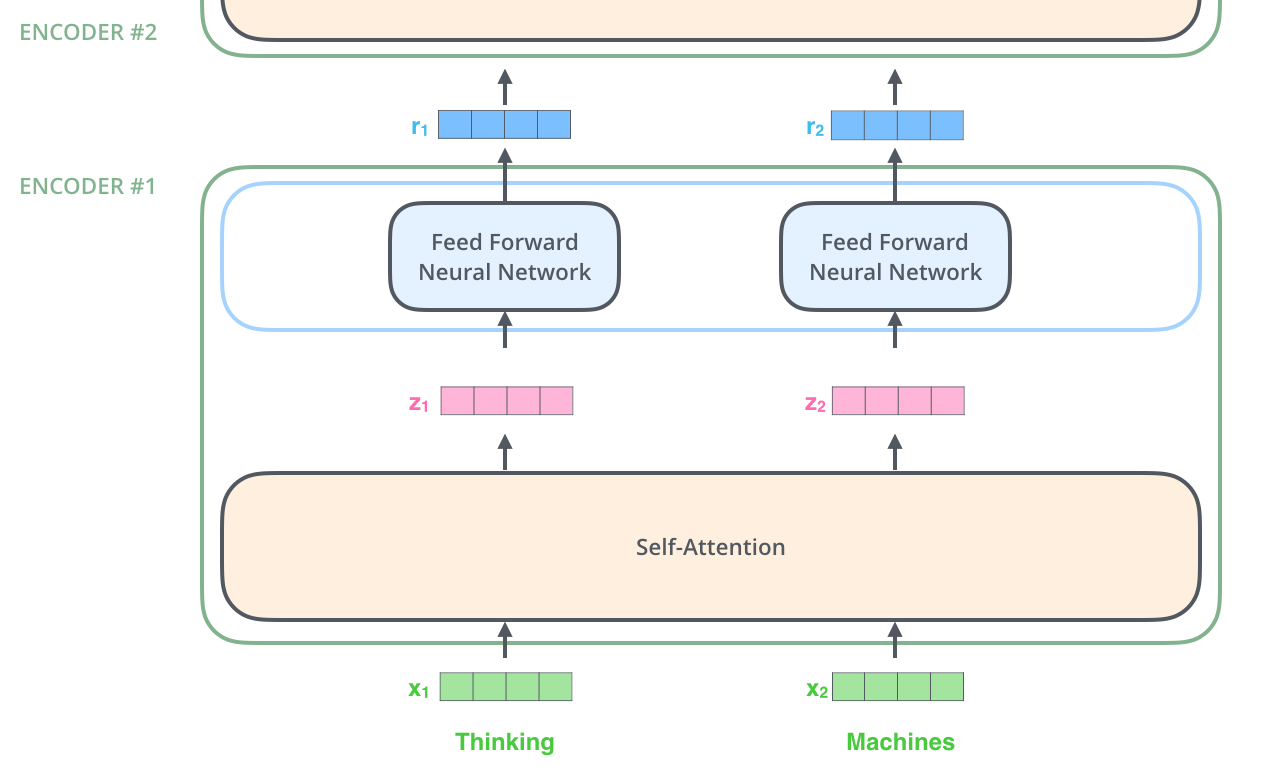
D.2 Self-Attention
D.2.1 Überblick
Bitte lass dich nicht davon täuschen, dass ich den Begriff Self-Attention verwende, als wäre es ein Konzept, das jeder kennt. Ich bin selbst erst auf das Konzept gestoßen, als ich das Paper Attention is All You Need gelesen habe. Lassen Sie uns herausarbeiten, wie es funktioniert.
Angenommen, der folgende Satz ist ein Eingabesatz, den wir übersetzen möchten:
"The animal didn't cross the street because it was too tired."Worauf bezieht sich “it” in diesem Satz? Bezieht es sich auf “street” oder “animal”? Für einen Menschen ist das eine einfache Frage, aber nicht für einen Algorithmus.
Wenn das Modell das Wort “it” verarbeitet, erlaubt es Self-Attention, das “it” mit “animal” zu verknüpfen.
Während das Modell jedes Wort in der Eingabesequenz verarbeitet, ermöglicht ihm Self-Attention, sich andere Wörter in der Eingabesequenz anzusehen, um Hinweise zu finden, die zu einer besseren Codierung dieses Wortes führen können.
Wenn Sie RNNs kennen, überlegen Sie, wie das Aufrechterhalten eines versteckten Zustands einem RNN ermöglicht, seine Repräsentation früherer Wörter/Vektoren, die es verarbeitet hat, in das aktuelle Wort zu integrieren. Für den Transformer ist Self-Attention die Methode, um das “Verständnis” anderer relevanter Wörter in das aktuelle Wort zu integrieren.

D.2.2 Schritt für Schritt
Wir schauen zunächst, wie Self-Attention mit Vektoren berechnet wird, und kommen dann dazu, wie sie eigentlich implementiert ist: mit Matrizen.
Der erste Schritt bei der Berechnung von Self-Attention ist, aus jedem Eingabevektor des Encoders (also die Word Embeddings) drei Vektoren zu erstellen. Für jedes Wort erstellen wir also einen Query-Vektor, einen Key-Vektor und einen Value-Vektor. Diese Vektoren werden erstellt, indem wir die Word Embedding mit drei Matrizen multiplizieren, die wir im Training trainiert haben.
Beachten Sie, dass diese neuen Vektoren in ihrer Dimension kleiner sind als der jeweilige Embedding-Vektor. Die neuen Vektoren haben Länge 64, während die Embedding- und Encoder-Eingabe-/Ausgabevektoren die Länge 512 haben. Sie müssen nicht unbedingt kleiner sein, dies ist eine Architekturentscheidung, um die Berechnung der Multi-Head-Attention (weitgehend) konstant zu halten.
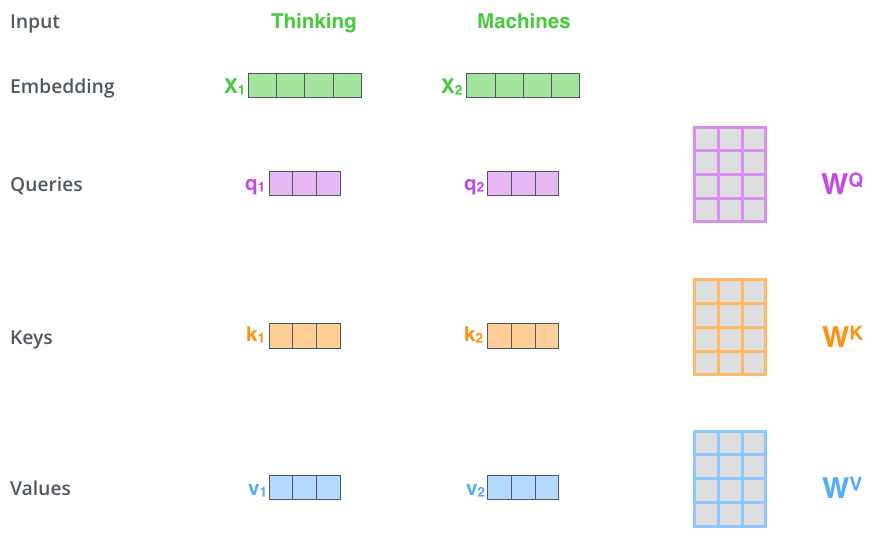
Was sind diese Query-, Key- und Value-Vektoren?
Es handelt sich um Abstraktionen, um “Attention” zu berechnen und zu verstehen. Sobald Sie gelesen haben, wie Attention berechnet wird, werden Sie im Wesentlichen alles wissen, was Sie über diese drei Vektoren wissen müssen.
Der zweite Schritt bei der Berechnung der Self-Attention besteht darin, einen Score zu berechnen. Angenommen, wir berechnen die Self-Attention für das erste Wort in diesem Beispiel: “Thinking”. Wir müssen jedes Wort des Eingabesatzes in Bezug auf dieses Wort bewerten. Der Score bestimmt, wie stark wir uns auf andere Teile des Eingabesatzes konzentrieren, während wir ein Wort an einer bestimmten Position kodieren.
Der Score wird berechnet, indem das Skalarprodukt des Query-Vektors mit dem Key-Vektor des entsprechenden zu bewertenden Wortes genommen wird. Wenn wir also die Self-Attention für das Wort an Position 1 verarbeiten, wäre der erste Score das Skalarprodukt von \(q_1\) und \(k_1\). Der zweite Score wäre das Skalarprodukt von \(q_1\) und \(k_2\).
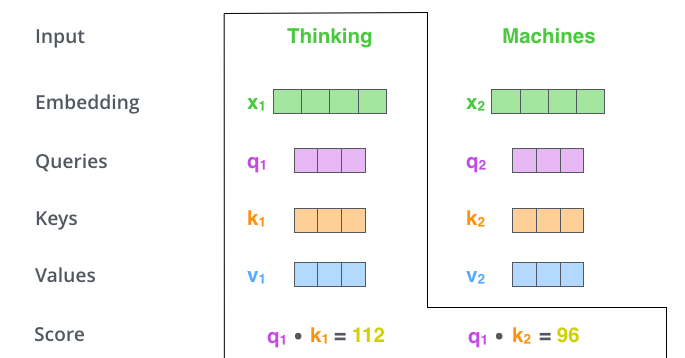
Der dritte und vierte Schritt bestehen darin, die Scores durch 8 zu teilen (die Wurzel der Dimension 64 der Key-Vektoren aus dem Paper). Dies führt zu stabileren Gradienten. Es könnten auch andere Werte verwendet werden, aber dies ist der Standardwert. Anschließend wird das Ergebnis durch mit Softmax transformiert. Softmax normalisiert die Scores, damit alle positiv sind und sich zu 1 summieren.
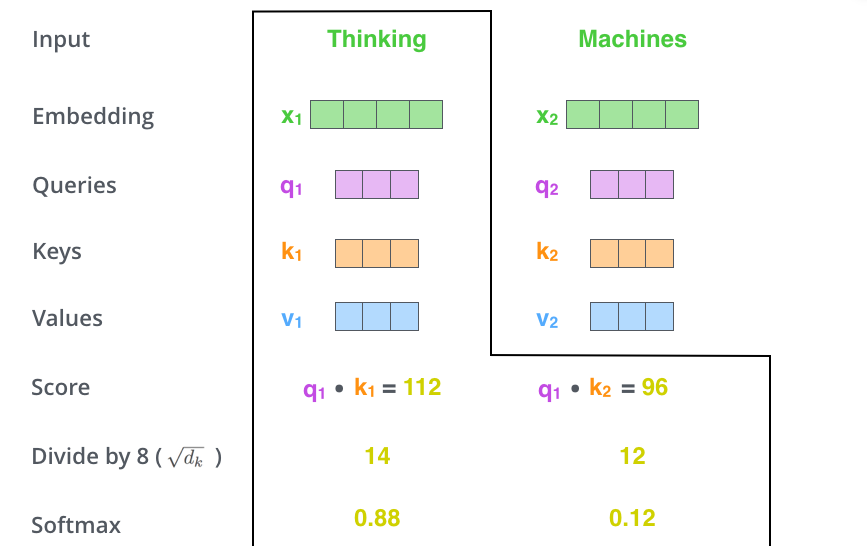
Dieser Softmax-Score bestimmt, wie stark sich jedes Wort in dieser Position einbringt. Offensichtlich wird das Wort, das sich selbst an dieser Position befindet, auch den höchsten Softmax-Score haben, aber manchmal ist es sinnvoll, sich zusätzlich auf ein anderes Wort zu fokussieren, das für das aktuelle Wort von Relevanz ist.

Der fünfte Schritt besteht darin, jeden Value-Vektor mit dem Softmax-Score zu multiplizieren (als Vorbereitung für ihre Aufsummierung). Die Intuition dabei ist, Werte von Wörtern, auf die wir fokussieren wollen, intakt zu lassen, und unwichtige Wörter abzuwürgen (indem wir sie mit ganz kleinen Zahlen wie 0.001 multiplizieren).
Der sechste Schritt besteht darin, die gewichteten Value-Vektoren aufzusummieren. Dies ist dann die Ausgabe der Self-Attention-Schicht an genau dieser Position (also hier für das erste Wort).
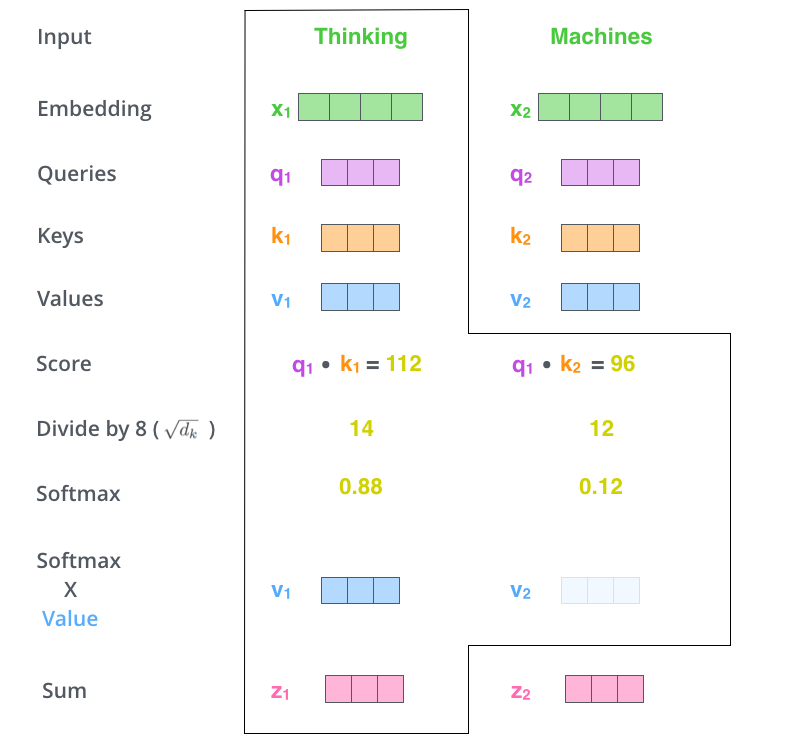
Damit ist die Berechnung der Self-Attention fertig. Der resultierende Vektor ist einer, den wir dem Feedforward-Netz übergeben können. In der tatsächlichen Implementierung wird diese Berechnung jedoch in Matrixform durchgeführt, da es eine schnellere Verarbeitung erlaubt. Nachdem wir die Intuition der Berechnung auf Wortebene verstanden haben, schauen wir uns das Ganze mit Matrizen an.
D.2.3 Matrixform
Der erste Schritt besteht darin, die Matrizen für Query, Key und Value zu berechnen. Dies tun wir, indem wir unsere Word Embeddings in eine Matrix \(X\) packen und sie mit den trainierten Gewichtsmatrizen \((W^Q, W^K, W^V)\) multiplizieren.
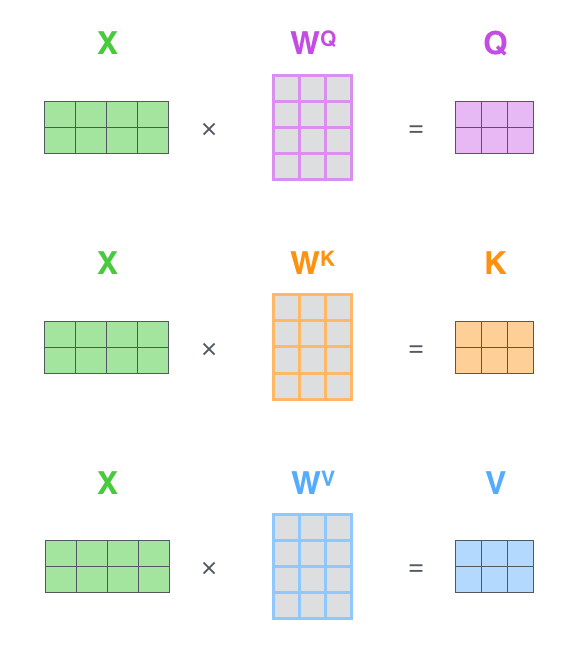
Schließlich können wir, da wir es mit Matrizen zu tun haben, die Schritte zwei bis sechs in einer Formel zusammenfassen, um die Ausgaben der Self-Attention-Schicht zu berechnen.
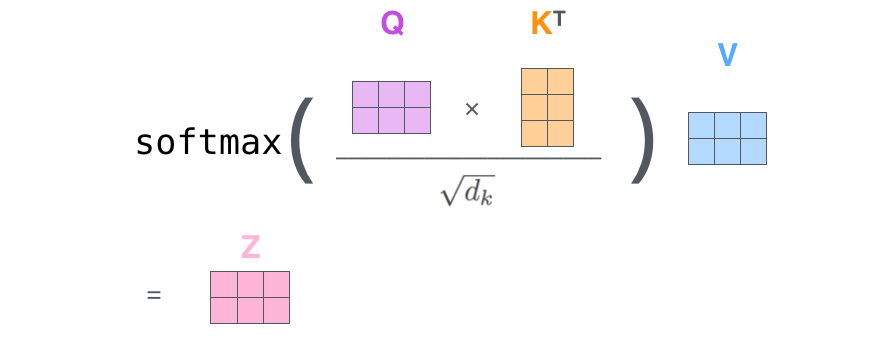
D.3 Ein Biest mit vielen Köpfen
In dem Paper wird die Self-Attention-Schicht mit einem Mechanismus namens “Multi-Headed-Attention” noch weiter verfeinert. Dies verbessert die Leistung der Attention-Schicht in zweierlei Hinsicht:
Es ermöglicht dem Modell, sich auf verschiedene Positionen zu fokussieren. Es stimmt schon, in dem obigen Beispiel enthält \(z_1\) ein wenig von jeder anderen Kodierung, aber es könnte vom aktuellen Wort dominiert werden. Wenn wir einen Satz übersetzen wie “The animal didn’t cross the street because it was too tired.”, wäre es nützlich zu wissen, auf welches Wort sich “it” bezieht.
Es gibt der Attention-Schicht mehrere “Repräsentations-Räume”. Wie wir als nächstes sehen werden, haben wir mit Multi-Headed-Attention nicht nur einen, sondern mehrere Sets von Query/Key/Value-Gewichtsmatrizen (der Transformer verwendet acht Attention Heads, sodass wir für jeden Encoder/Dekoder acht solcher Sets erhalten). Jeder dieser Sets wird zufällig initialisiert. Dann werden nach dem Training alle Sets verwendet, um die Eingabe-Embeddings (oder Vektoren aus niedrigeren Encodern/Dekodern) in einen anderen Repräsentations-Raum zu projizieren.
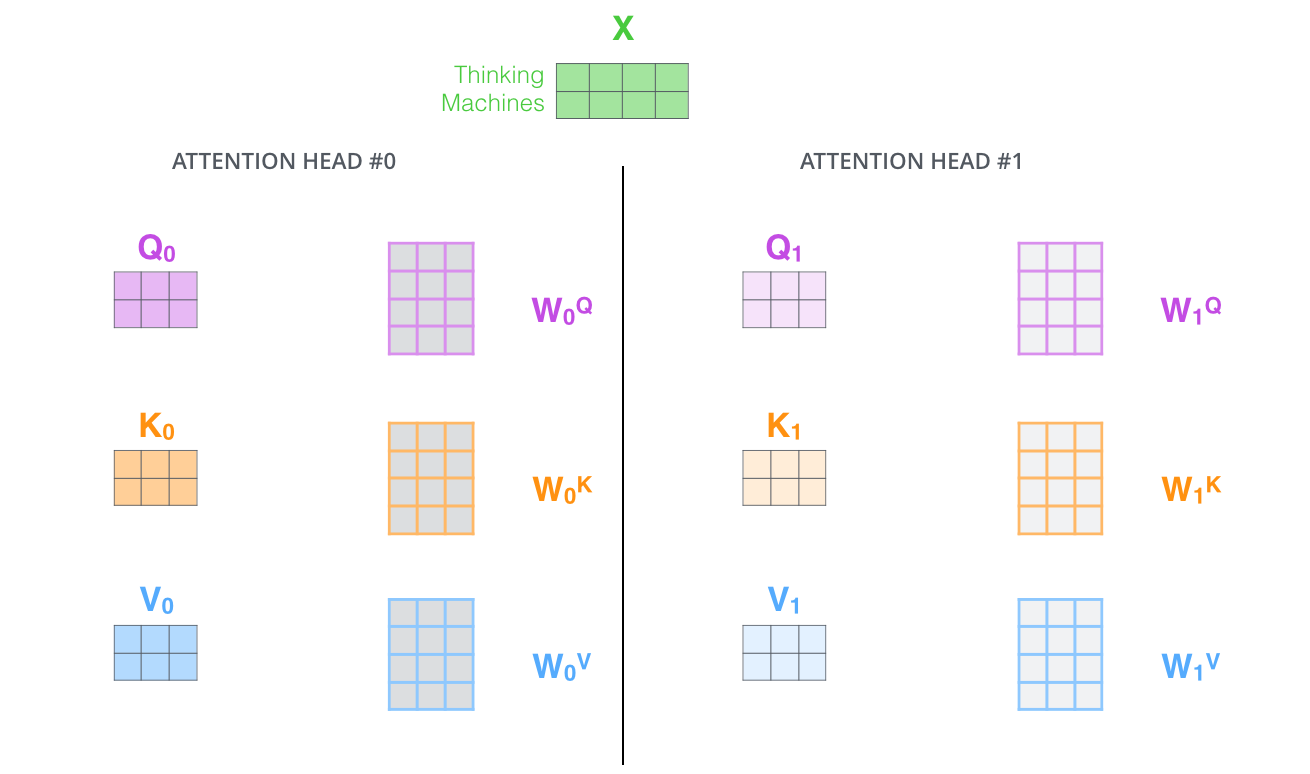
Wenn wir dieselbe Self-Attention-Berechnung durchführen, die wir oben skizziert haben, nur acht verschiedene Male mit verschiedenen Gewichtsmatrizen, erhalten wir acht verschiedene \(Z\)-Matrizen.
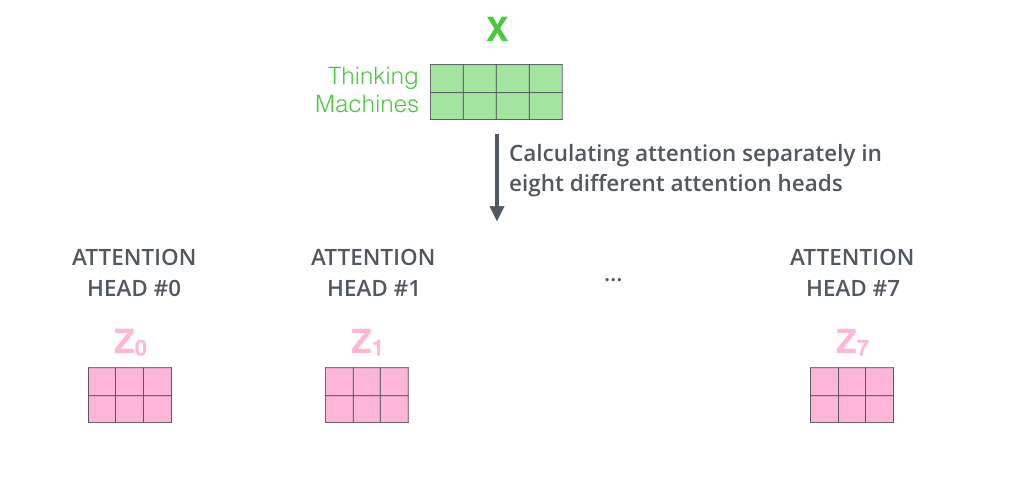
Jetzt haben wir ein Problem. Die Feedforward-Schicht erwartet nicht acht Matrizen, sondern eine einzelne Matrix (einen Vektor für jedes Wort). Also müssen wir einen Weg finden, diese acht Matrizen in eine einzige Matrix zu pressen.
Was machen wir? Wir konkatenieren die Matrizen und multiplizieren sie mit einer zusätzlichen Gewichtsmatrix \(W^O\).
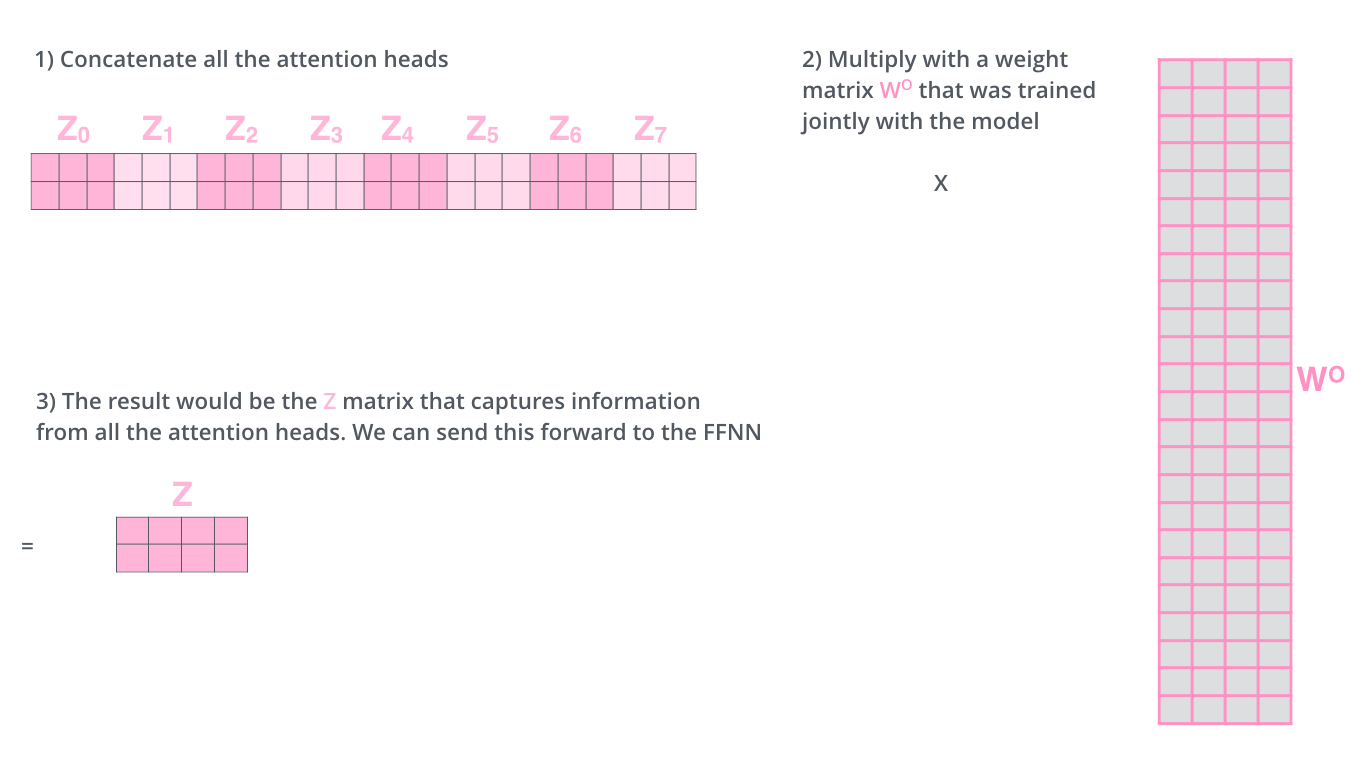
Das ist im Grund alles, was man zur Multi-Headed-Self-Attention wissen muss. Es sind ziemlich viele Matrizen, ist schon klar. Lassen Sie mich versuchen, alle in einem Diagramm zusammenzufassen, damit wir alles auf einen Blick sehen.
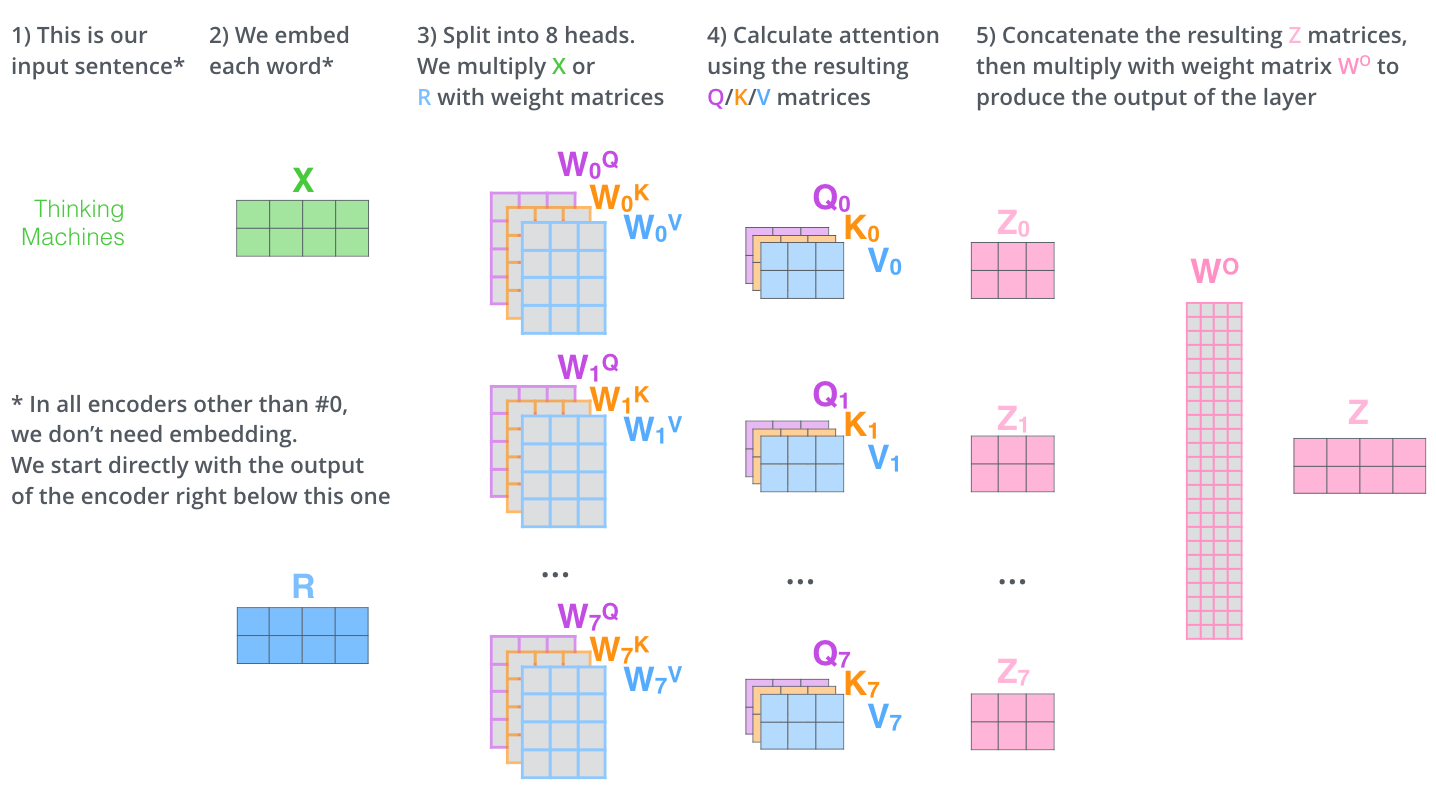
Nachdem wir die Attention Heads besprochen haben, wollen wir unser Beispiel von vorher noch einmal betrachten, um zu sehen, auf welche Bereiche sich die verschiedenen Attention Heads fokussieren, während wir das Wort “it” in unserem Beispielsatz kodieren:

Wenn wir alle Attention Heads ins Diagramm bringen, werden die Dinge schon schwerer zu interpretieren:
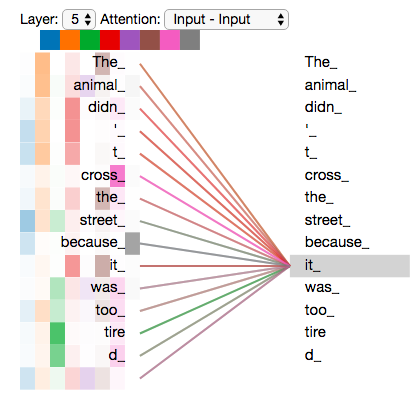
D.4 Positionsenkodierung und Residual Connections
D.4.1 Reihenfolge repräsentieren mit Positionsenkodierung
Was im bislang beschriebenen Modell fehlt, ist eine Möglichkeit, die Reihenfolge der Wörter im Eingabesatz zu berücksichtigen.
Um dieses Problem anzugehen, fügt der Transformer jedem Word Embedding einen Vektor hinzu. Diese Vektoren folgen einem spezifischen Muster, das das Modell lernt, und dieses Muster hilft ihm, die Position jedes Wortes oder den Abstand zwischen verschiedenen Wörtern in der Sequenz zu verstehen. Die Intuition hierbei ist, dass das Hinzufügen dieser Werte zu den Word Embeddings sinnvolle Abstände zwischen den Embedding-Vektoren liefert, sobald sie auf Q/K/V-Vektoren projiziert werden und bei den weiteren Matrixoperationen.
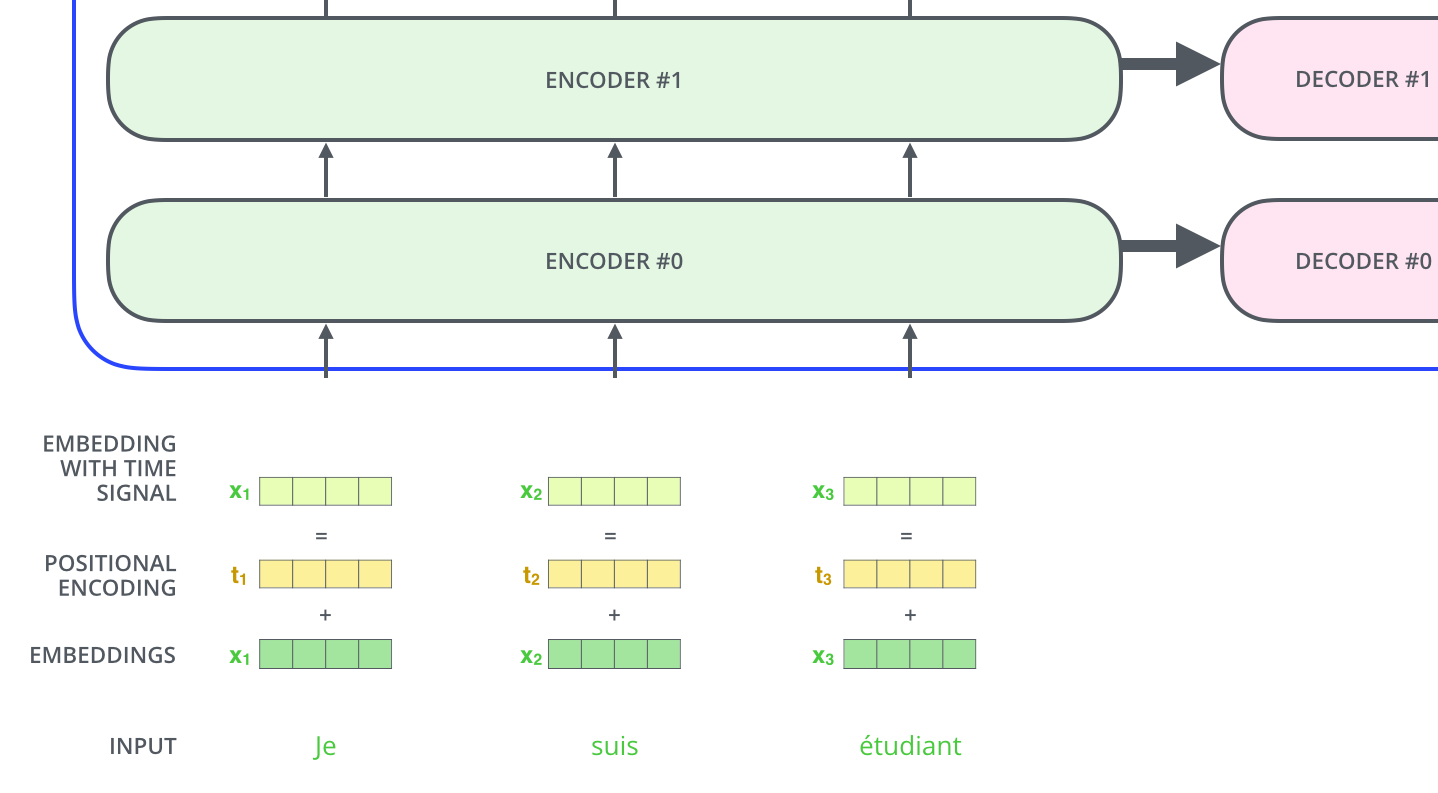
Wenn wir mal vereinfachte Word Embeddings mit Dimension 4 betrachten, würden die Positionskodierungen so aussehen:
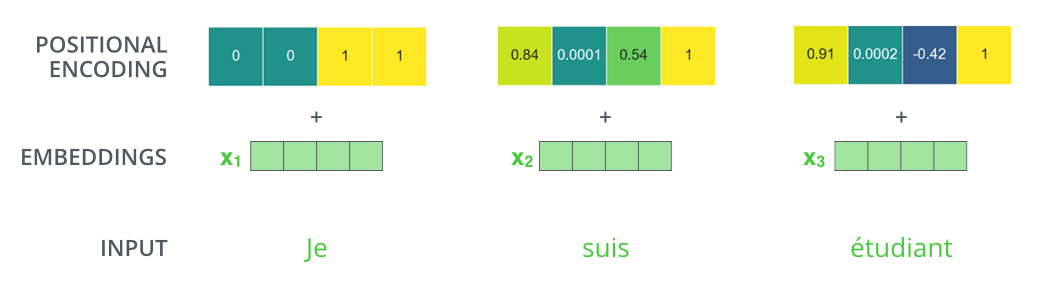
Wie könnte dieses Muster aussehen?
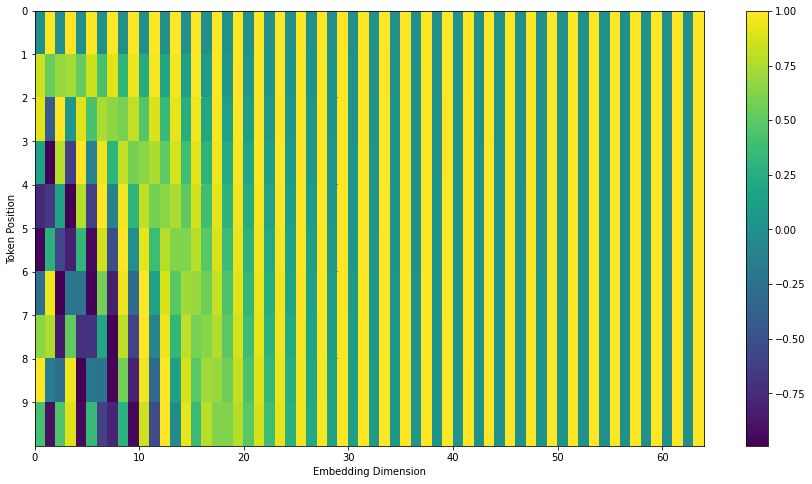
In der folgenden Abbildung entspricht jede Zeile einer Positionskodierung eines Vektors. Die erste Zeile wäre also der Vektor, den wir zur Embedding des ersten Wortes einer Eingabesequenz addieren würden. Jede Zeile enthält 512 Werte - jeweils mit einem Wert zwischen 1 und -1. Wir haben sie farblich kodiert, damit das Muster klar wird.
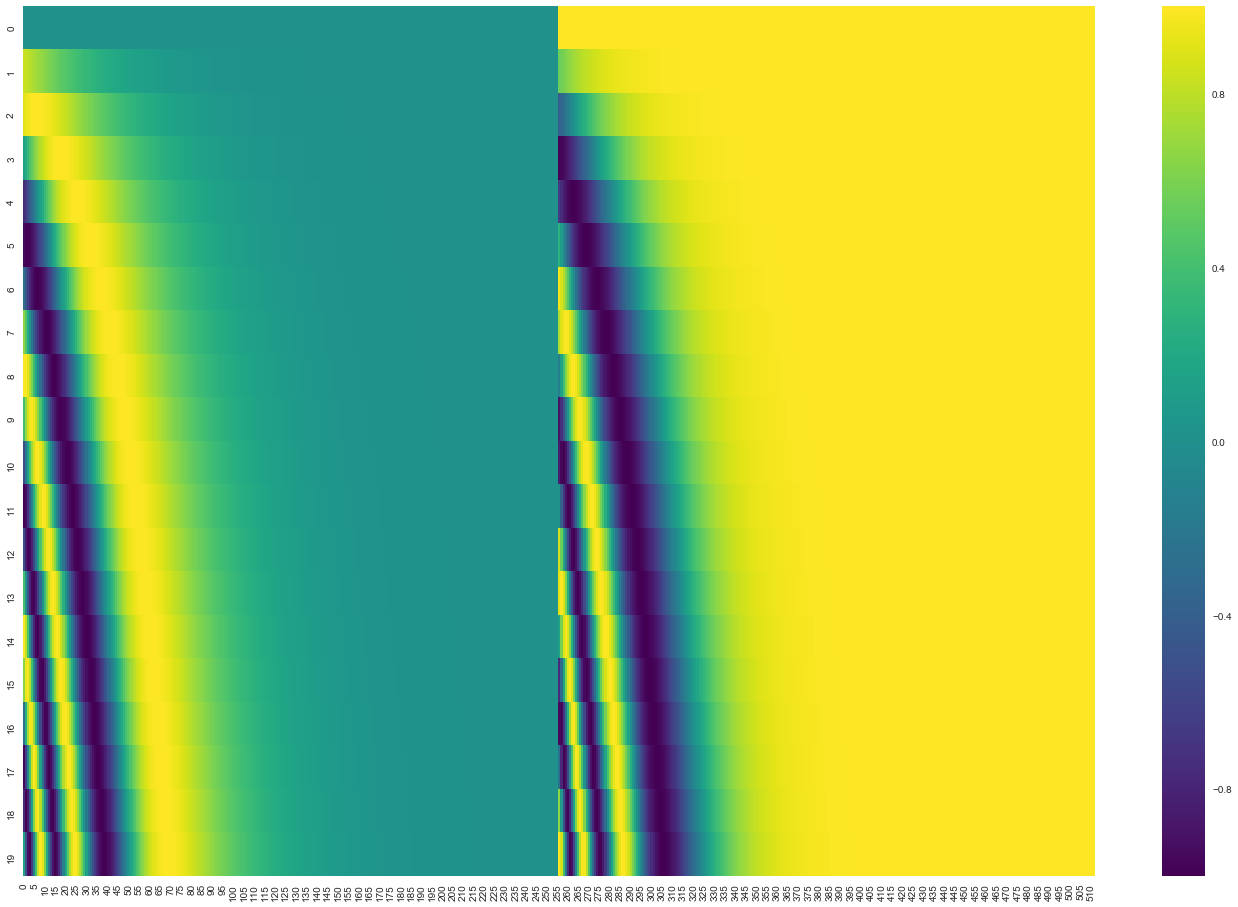
Die Formel für die Positionsenkodierung wird im Paper beschrieben (Abschnitt 3.5). Sie können den Code zur Generierung der Positionsencodierung in get_timing_signal_1d() sehen. Dies ist jedoch nicht die einzige mögliche Methode für die Positionsenkodierung. Sie bietet jedoch den Vorteil, sich auf beliebige Längen von Sequenzen skalieren zu lassen (z.B. wenn unser trainiertes Modell einen Satz übersetzen soll, der länger ist als jeder Satz im Trainingsdatensatz).
Update Juli 2020: Die oben gezeigte Positionsenkodierung stammt aus der Tensor2Tensor-Implementierung des Transformer. Die Methode im Paper ist etwas anders, da sie die zwei Signaltypen nicht zusammenfügt, sondern alternierend verschränkt, wie die folgende Abbildung zeigt. Hier ist der Code zur Generierung:
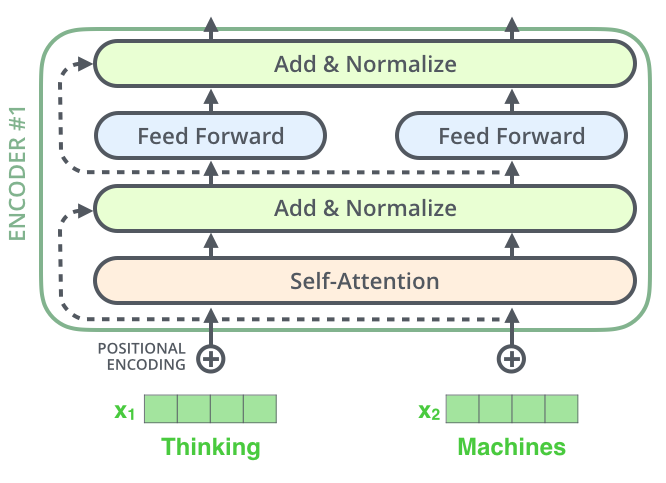
D.4.2 Residual Connections
Ein Detail in der Architektur des Encoders, das wir erwähnen sollten, ist, dass jede Schicht innerhalb eines Encoders (Self-Attention und Feedforward) eine Residual Connection als “Umgehung” um sie herum hat. Anschließend wird Layer Normalisation durchgeführt.
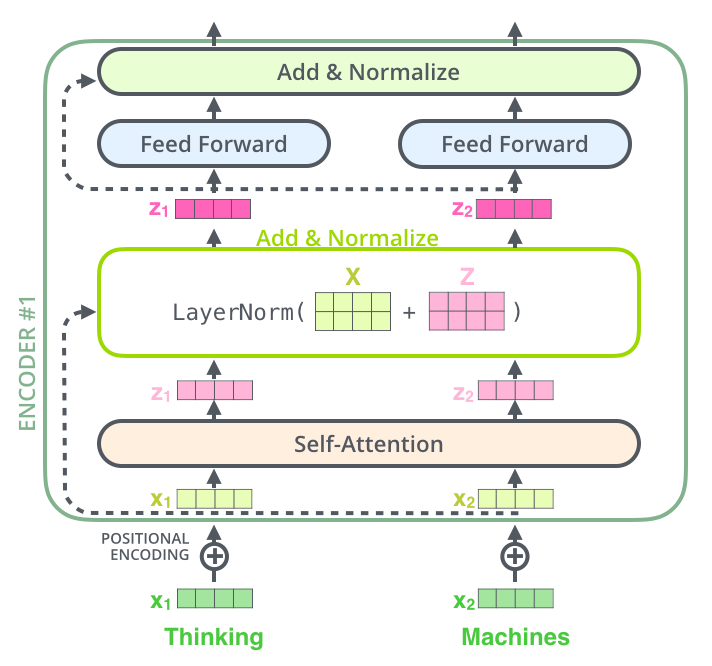
Wenn wir die Vektoren und die Layer-Normalization-Operation, die mit der Self-Attention verbunden sind, visualisieren wollen, sieht das so aus:
Das gleiche gilt für die Schichten der Decoder. Wenn wir uns einen Transformer mit je zwei Encodern und Decodern vorstellen, sieht das so aus:
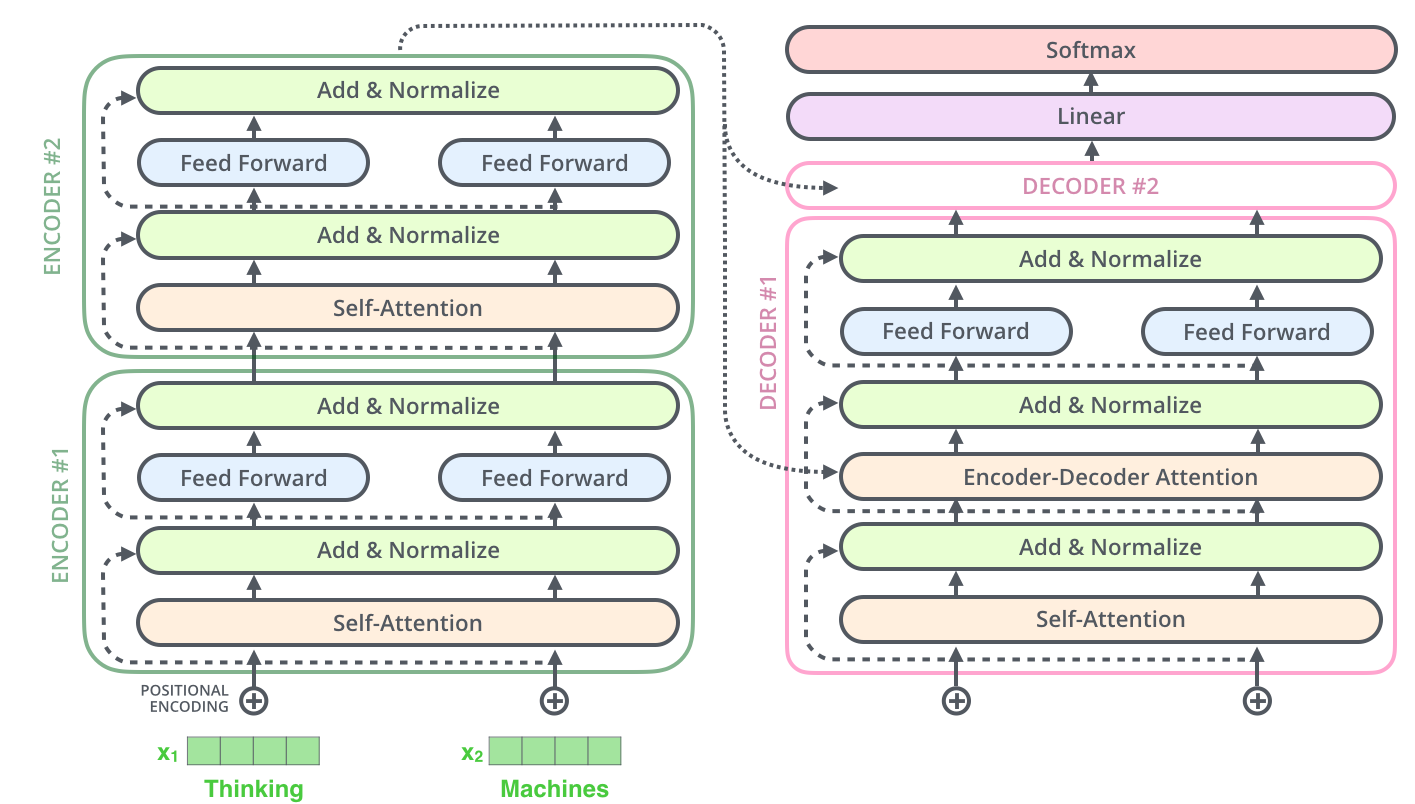
D.5 Decoder und Training
D.5.1 Die Decoder-Seite
Nun, da wir die meisten Konzepte auf der Encoder-Seite behandelt haben, wissen wir im Grunde auch, wie die Komponenten des Decoders funktionieren. Aber lassen Sie uns einen Blick darauf werfen, wie sie zusammenarbeiten.
Der Encoder beginnt mit der Verarbeitung der Eingabesequenz. Die Ausgabe des oberen Encoders wird dann in einen Satz von Aufmerksamkeitsvektoren \(K\) und \(V\) transformiert. Diese sollen von jedem Decoder in seiner Encoder-Decoder-Attention-Schicht verwendet werden, um dem Decoder zu helfen, sich auf geeignete Stellen in der Eingabesequenz zu fokussieren:
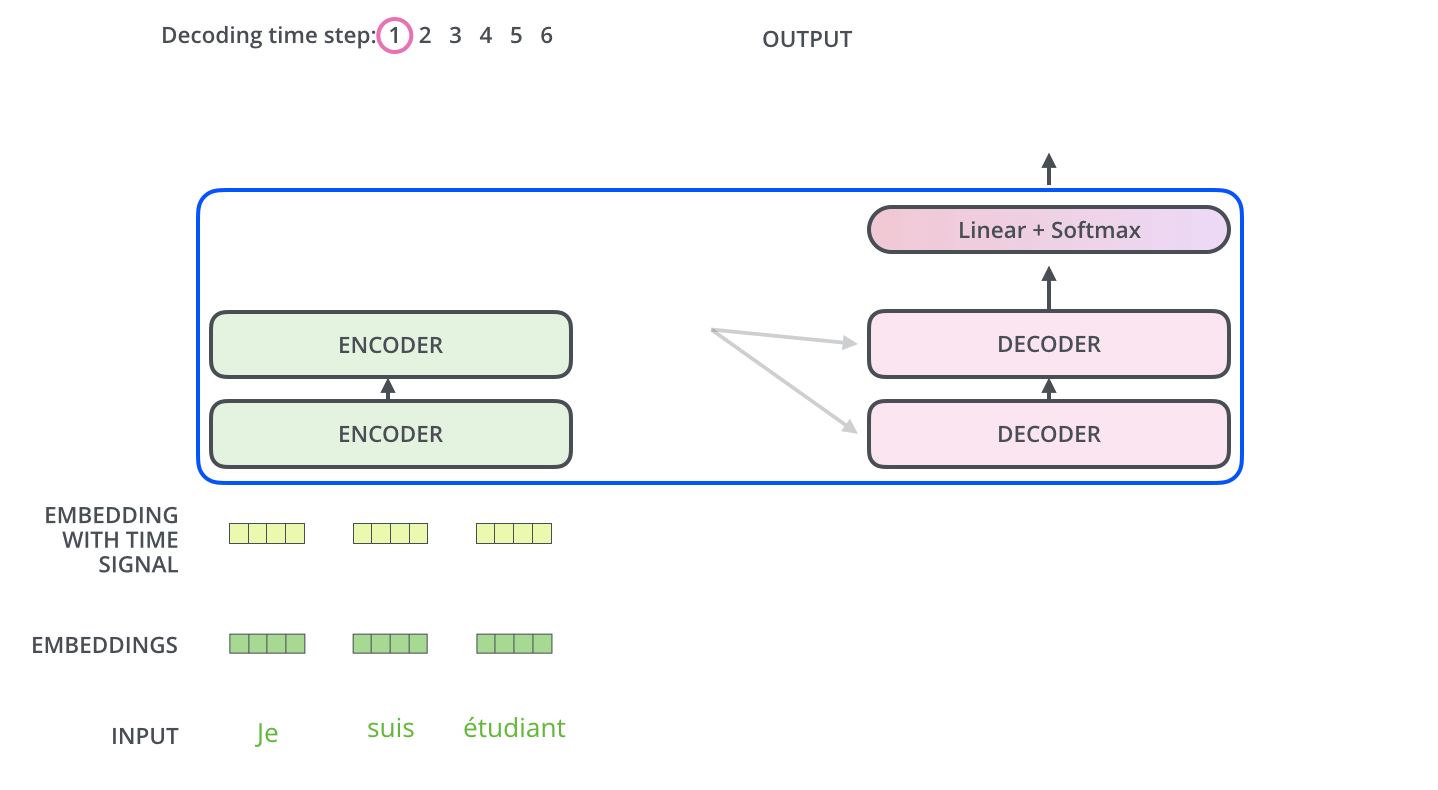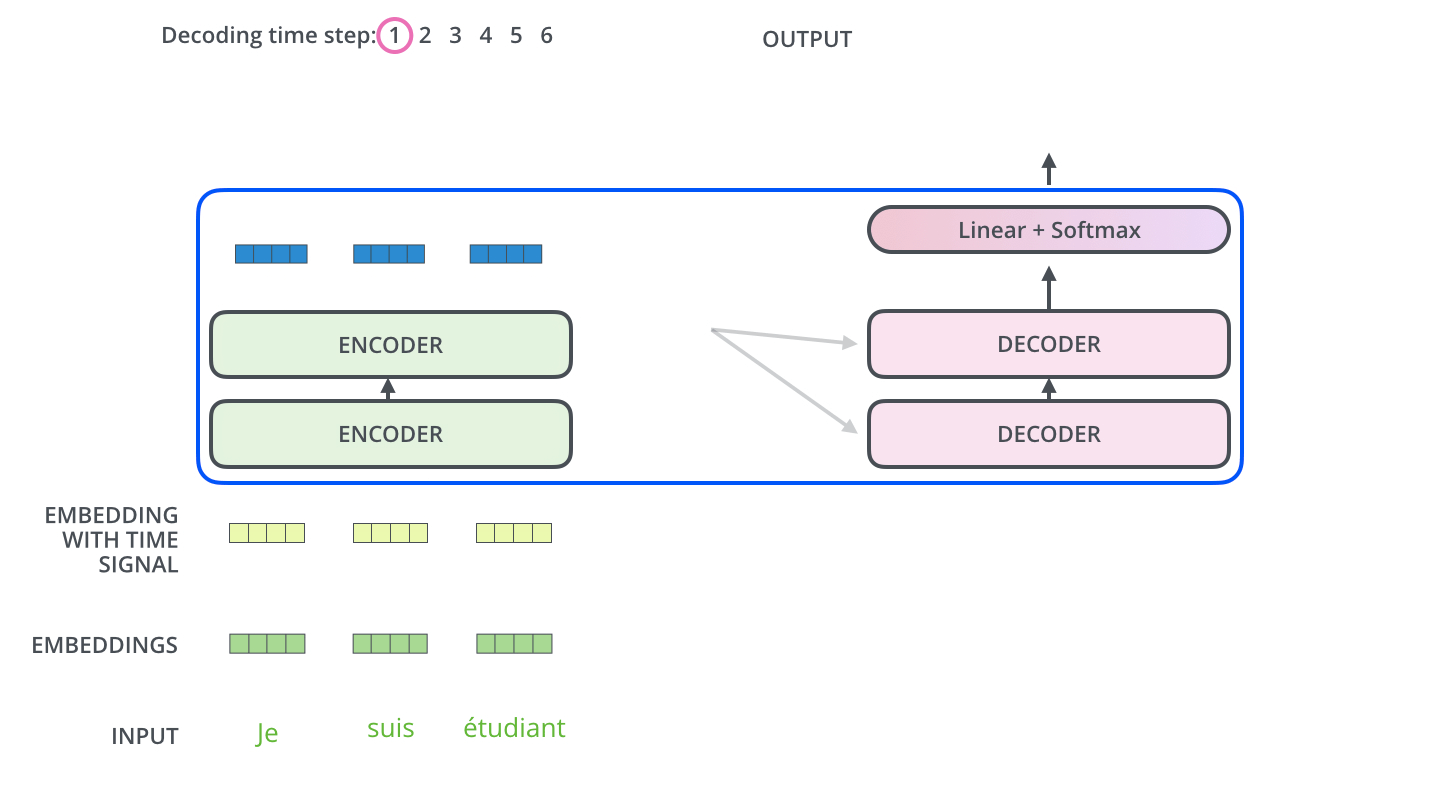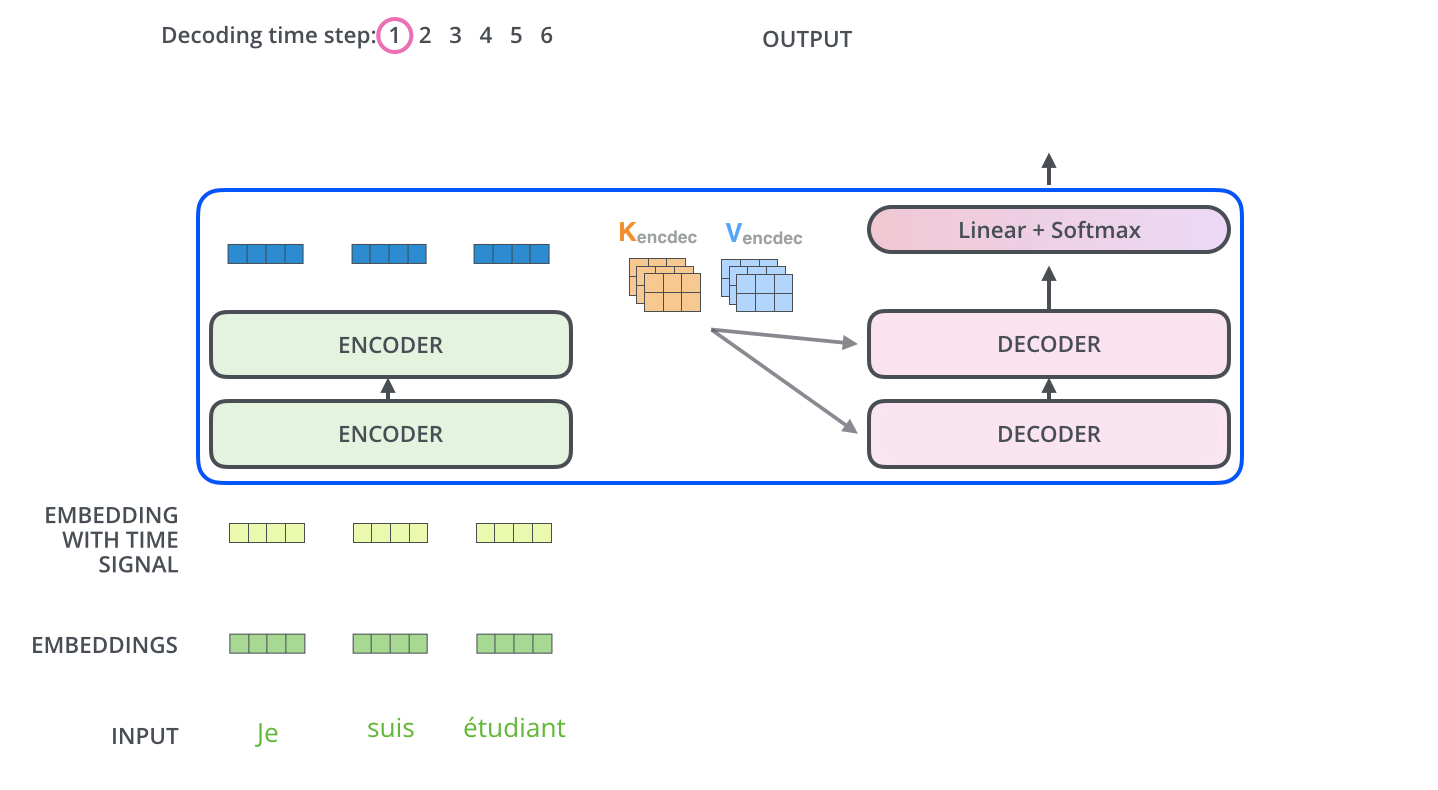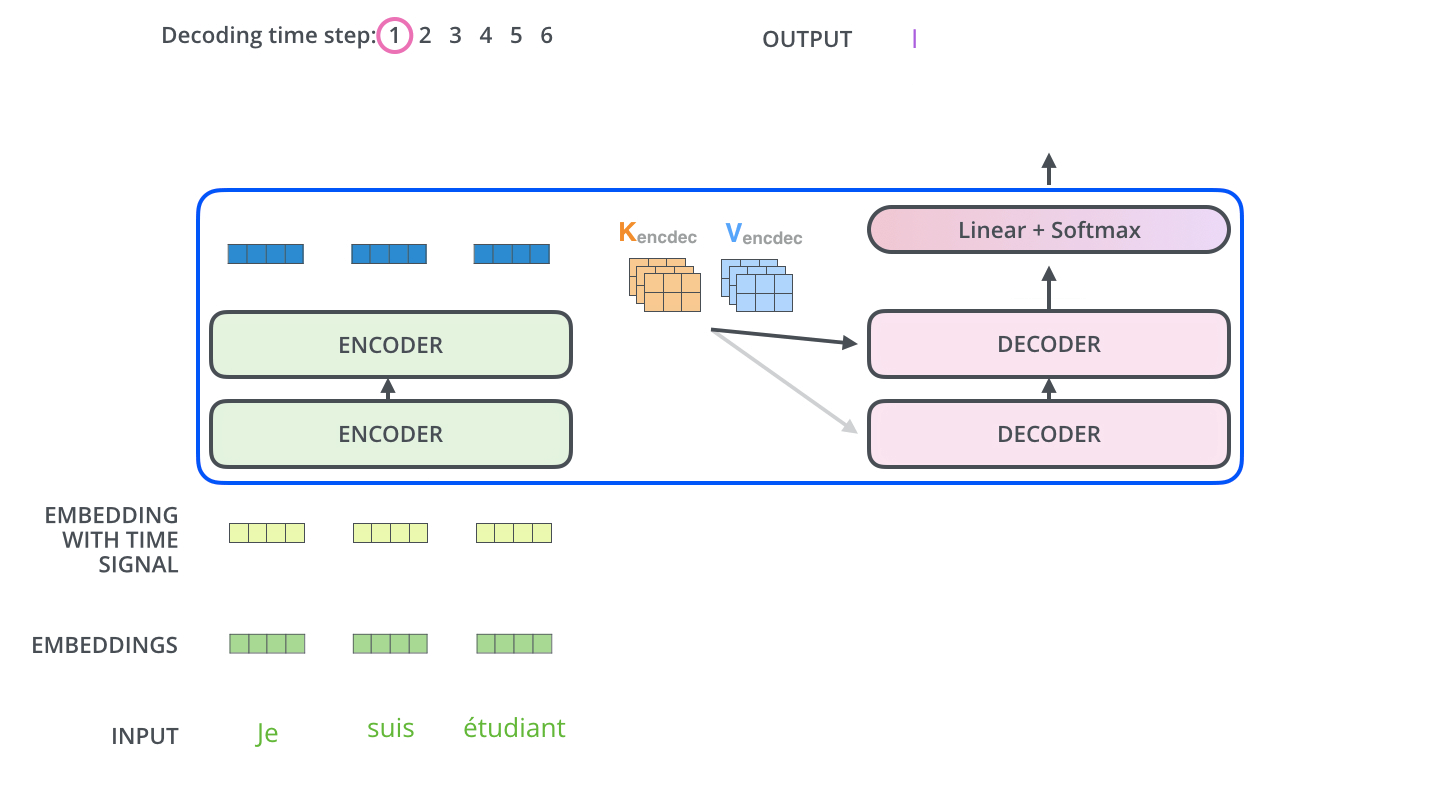
Die folgenden Schritte wiederholen das Ganze so lange, bis ein spezielles Symbol erreicht ist, das anzeigt, dass der Decoder seine Ausgabe erledigt hat. Die Ausgabe von jedem Schritt wird dem untersten Decoder im nächsten Zeitschritt zugeführt, und die Decoder geben ihre Zwischenergebnisse genauso weiter, wie es die Encoder tun. Und genauso wie wir es mit den Eingaben der Encoder gemacht haben, überführen wir die Decoder-Eingaben in Word Embeddings und fügen ihnen Positionsenkodierungen hinzu, um die Reihenfolge jedes Wortes zu integrieren.
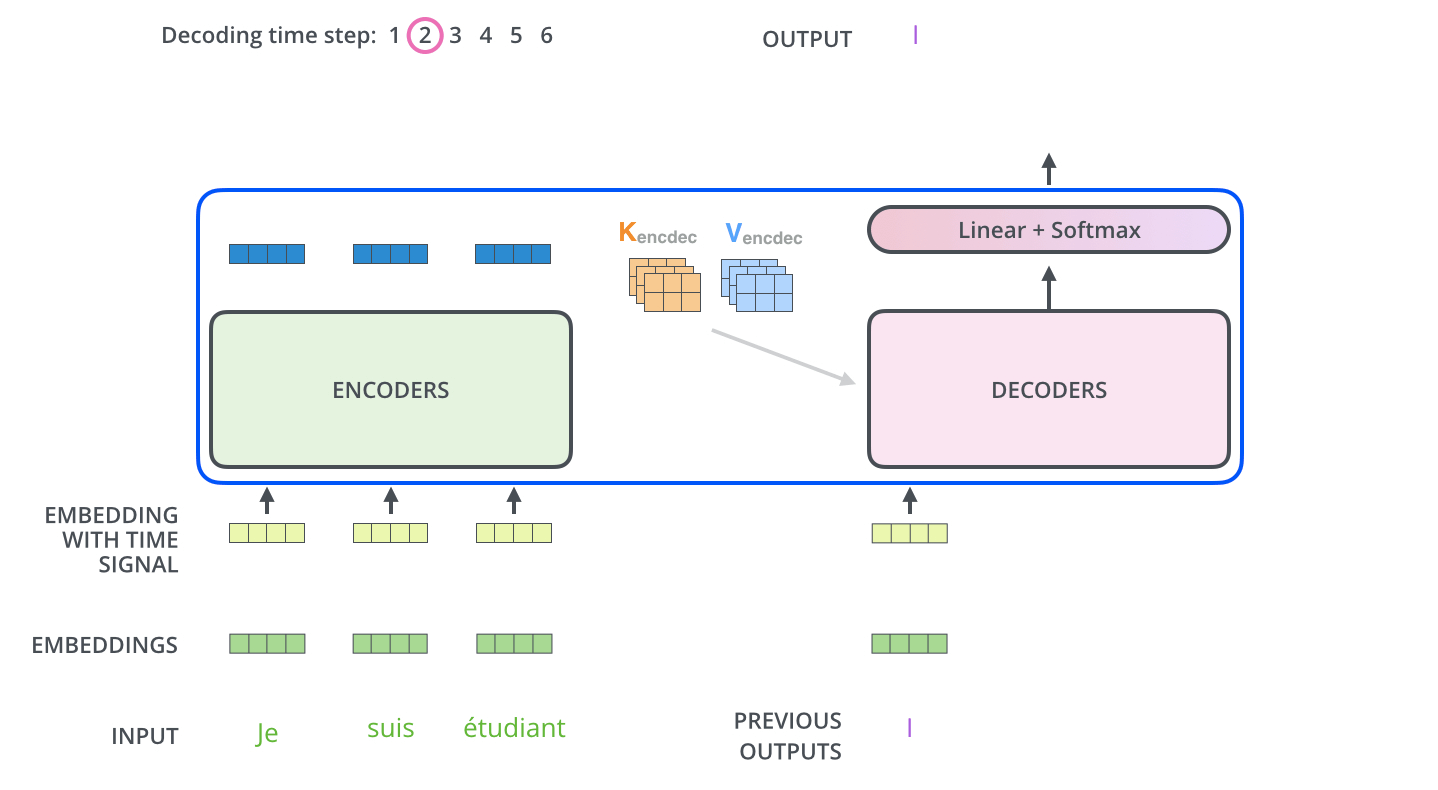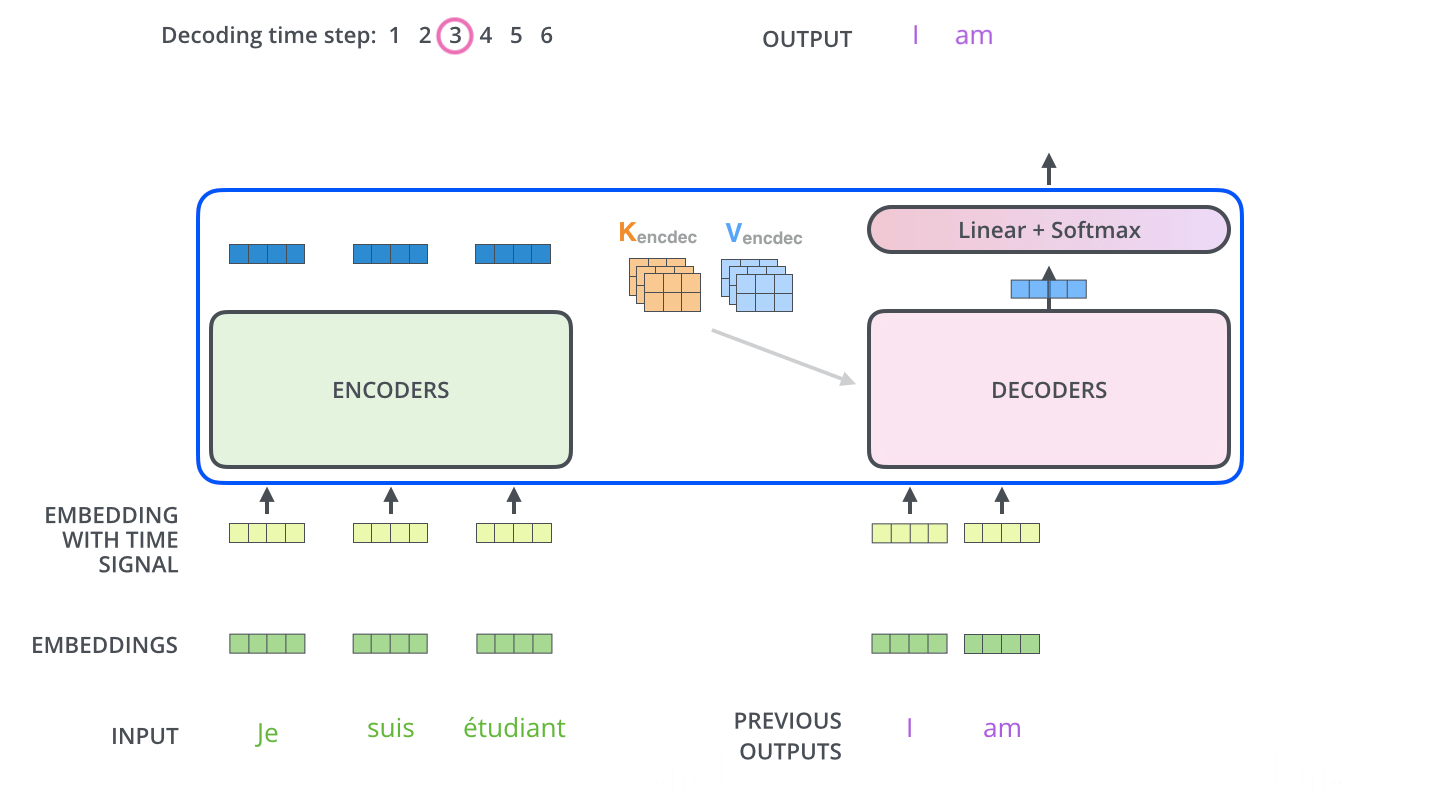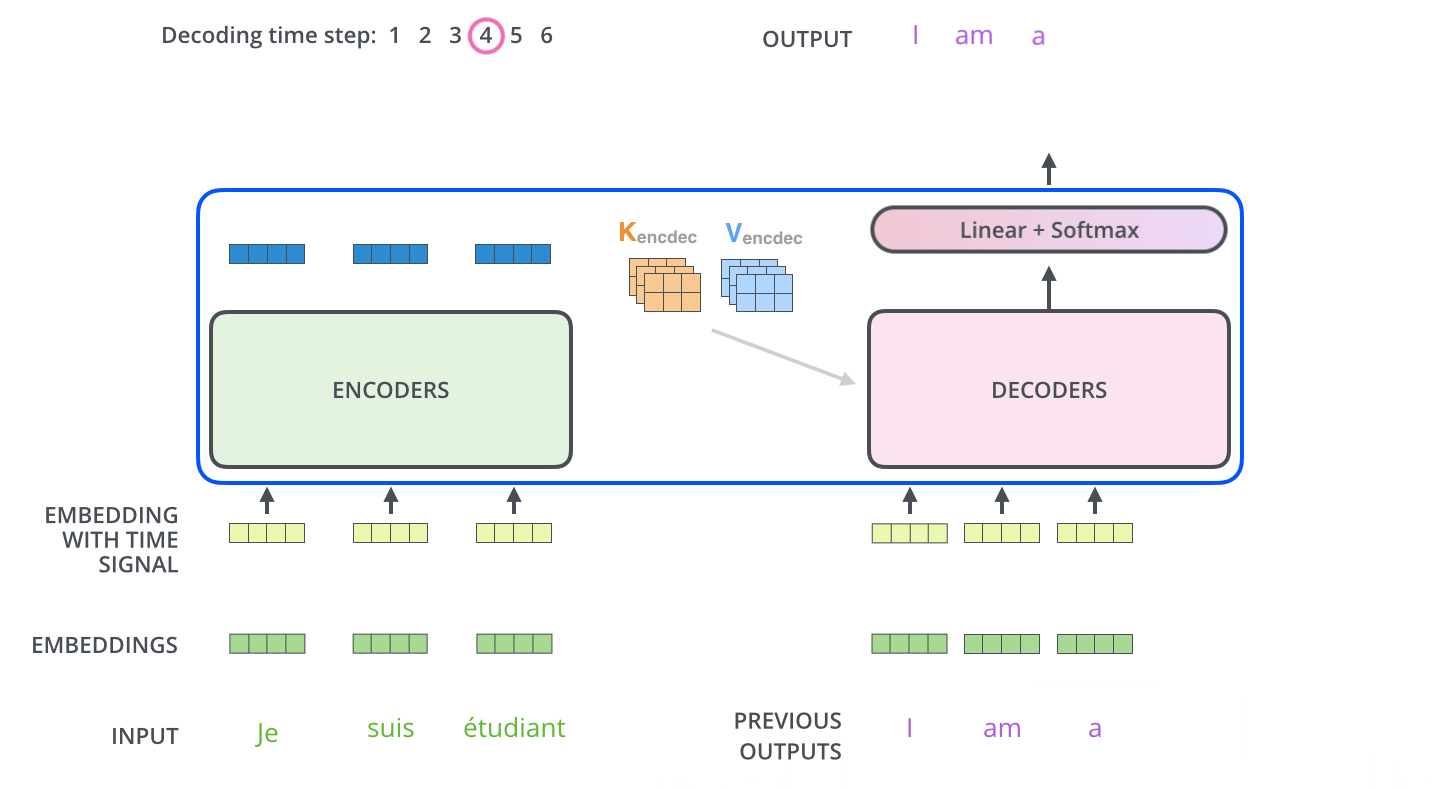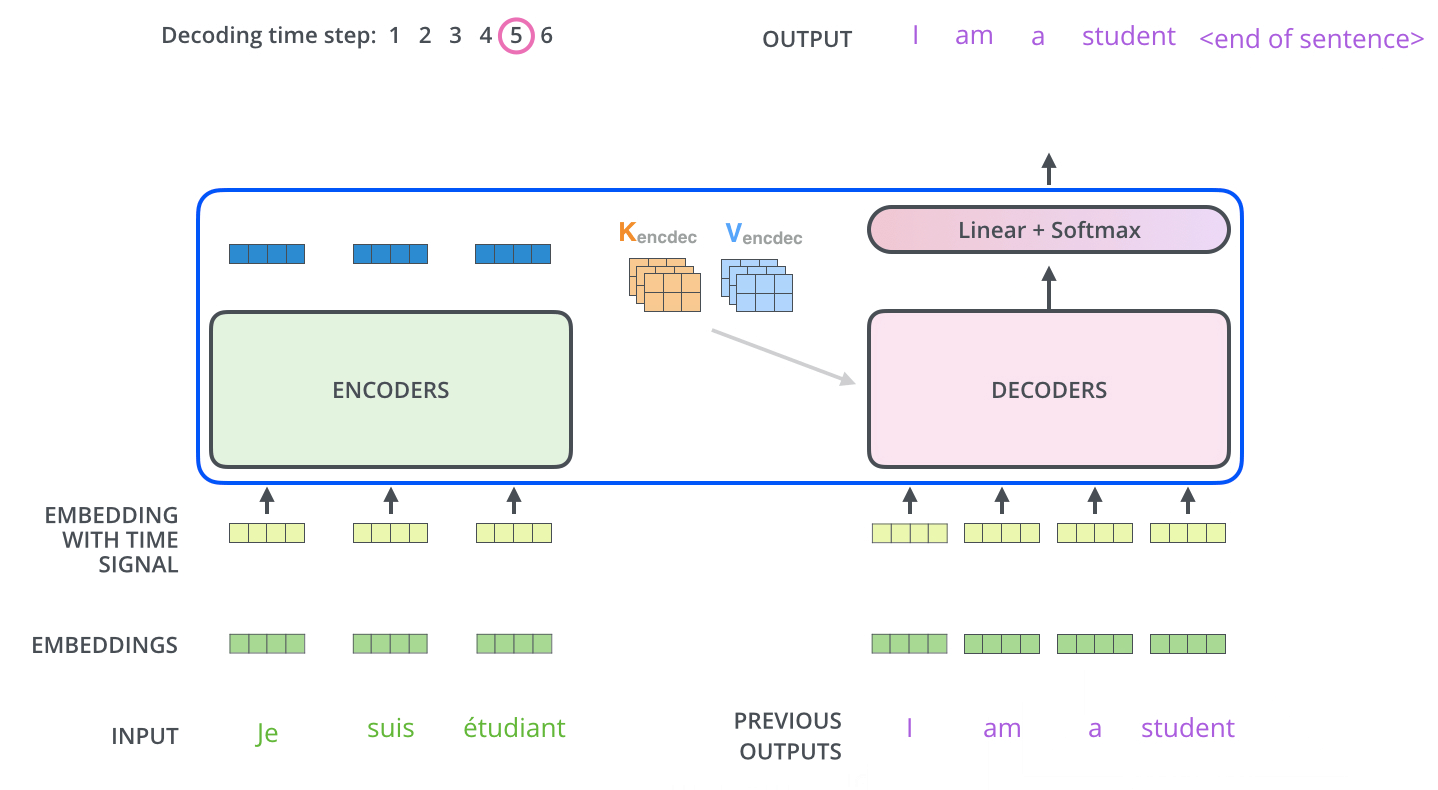
Die Self-Attention-Schichten im Decoder arbeiten etwas anders als die im Encoder:
Im Decoder darf die Self-Attention-Schicht nur auf frühere Positionen in der Ausgabesequenz achten. Dies wird durch Maskierung zukünftiger Positionen (indem sie auf “minus unendlich”, also -inf, gesetzt werden) vor dem Softmax-Schritt in der Self-Attention-Berechnung erreicht.
Die Encoder-Dekoder-Attention-Schicht funktioniert genauso wie die Multi-Headed-Self-Attention, außer dass sie ihre Queries-Matrix aus der darunterliegenden Schicht erstellt und die Keys- und Values-Matrix aus der Ausgabe des Encoder-Teils übernimmt.
D.5.2 Die letzte Schicht
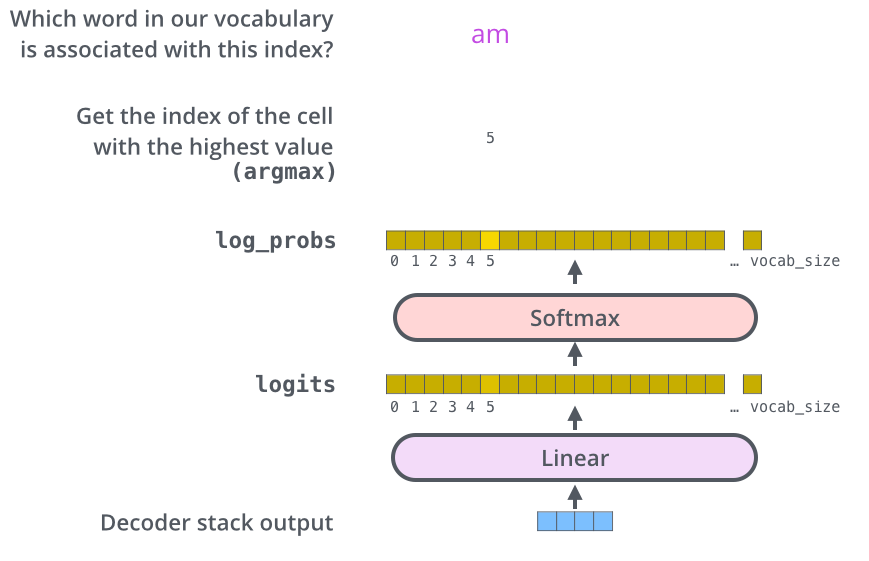
Die Decoder-Reihe gibt einen Vektor von Gleitkommazahlen aus. Wie verwandeln wir das in ein Wort? Das ist die Aufgabe der letzten linearen Schicht, die von einer Softmax-Schicht gefolgt wird.
Die lineare Schicht ist “fully connected”. Sie wandelt den Vektor, der von der Decoder-Reihe erzeugt wird, in einen viel, viel größeren Vektor, der als Logits-Vektor bezeichnet wird.
Nehmen wir an, unser Modell kennt 10.000 eindeutige englische Wörter (das Ausgabe-Vokabular unseres Modells), die es aus seinem Trainingsdatensatz gelernt hat. Dies würde den Logits-Vektor 10.000 Zellen breit machen - jede Zelle entspricht der Punktzahl eines eindeutigen Wortes. So interpretieren wir die Ausgabe des Modells und der linearen Schicht.
Die Softmax-Schicht wandelt dann diese Punktzahlen in Wahrscheinlichkeiten um (alle positiv, die Summe beträgt 1). Die Zelle mit der höchsten Wahrscheinlichkeit wird ausgewählt, und das damit verbundene Wort wird als Ausgabe für diesen Zeitschritt erzeugt.
D.5.3 Recap des Trainings
Jetzt, da wir den gesamten Vorwärtsdurchlauf durch einen trainierten Transformer abgedeckt haben, wäre es nützlich, einen Blick auf die Intuition des Trainings des Modells zu werfen.
Während des Trainings durchläuft ein untrainiertes Modell dieselbe Vorwärtsverarbeitung. Da wir es jedoch mit einem gelabelten Trainingsdatensatz trainieren, können wir seine Ausgabe mit der korrekten Ausgabe vergleichen.
Um dies zu verdeutlichen, nehmen wir an, dass unser AusgabAusgabe-Vokabular nur sechs Wörter enthält: “a”, “am”, “I”, “thanks”, “student” und “<eos>” (steht für end of sentence).
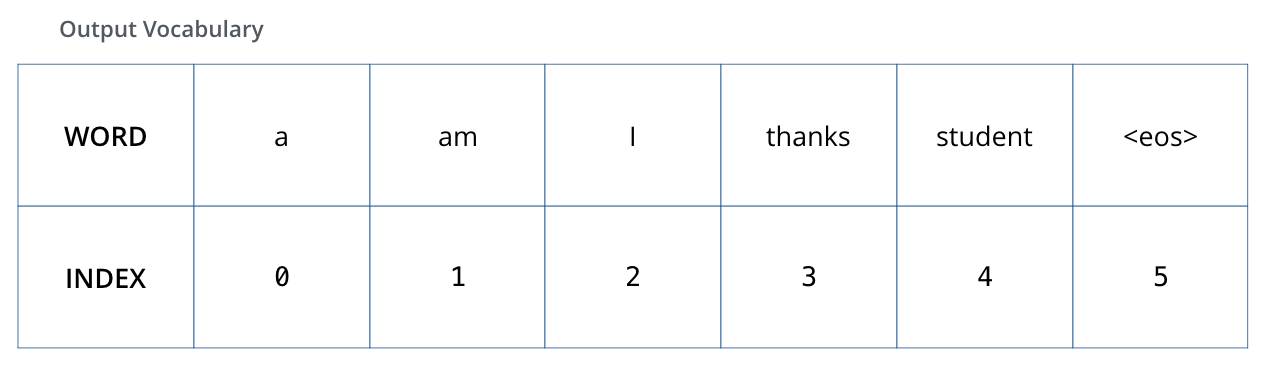
Nachdem wir unser Ausgabe-Vokabular definiert haben, können wir einen Vektor derselben Länge verwenden, um jedes Wort in unserem Vokabular zu indizieren. Dies wird auch als One-Hot-Encoding bezeichnet. So können wir beispielsweise das Wort “am” mit dem folgenden Vektor repräsentieren:
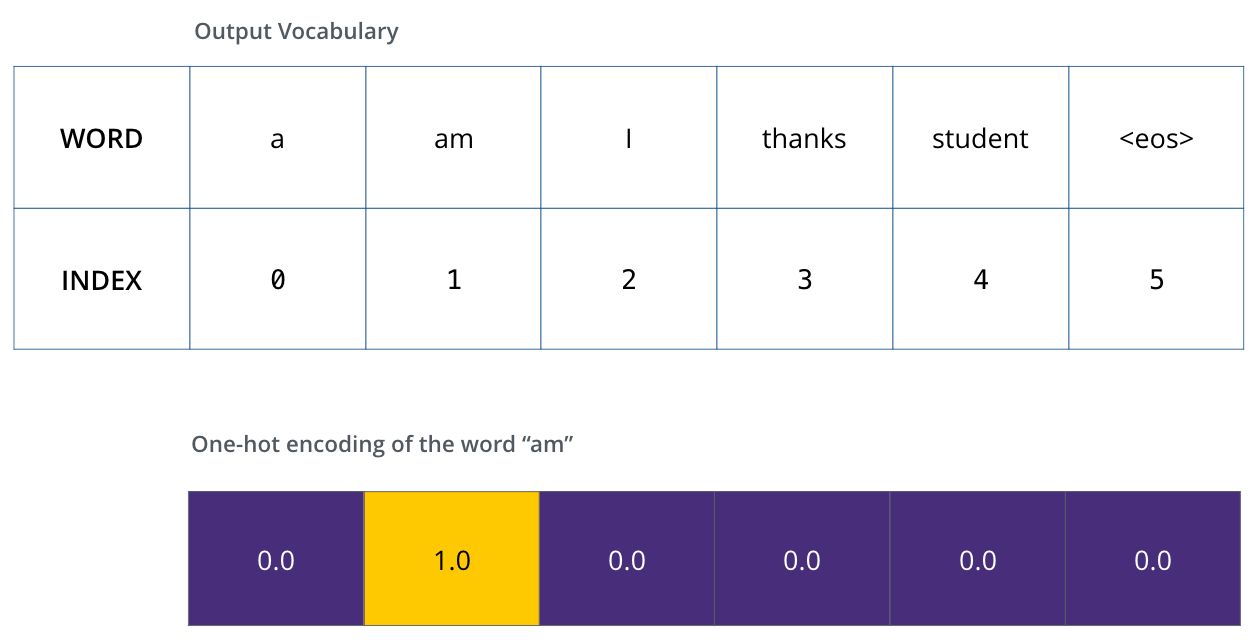
Nach diesem Recap wollen wir die Verlustfunktion des Modells besprechen - die Metrik, die wir während der Trainingsphase optimieren, um zu einem trainierten und hoffentlich erstaunlich genauen Modell zu gelangen.
D.5.4 Die Verlustfunktion
Angenommen, wir trainieren unser Modell. Angenommen, es ist unser erster Schritt in der Trainingsphase, und wir trainieren es an einem einfachen Beispiel - das Wort “merci” in “thanks” zu übersetzen.
Das bedeutet, wir möchten eine Wahrscheinlichkeitsverteilung als Ausgabe erhalten, die auf das Wort “thanks” hindeutet. Da das Modell noch nicht trainiert ist, wird das wahrscheinlich noch nicht passieren.
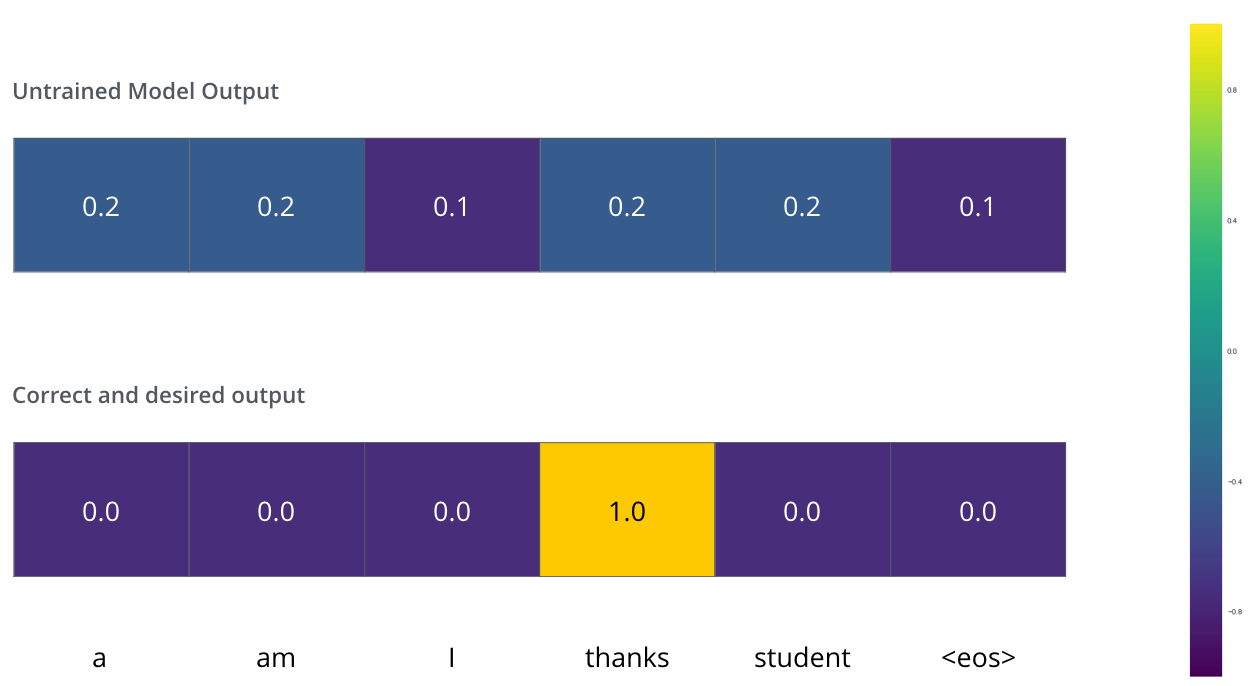
Wie vergleichen wir zwei Wahrscheinlichkeitsverteilungen? Wir subtrahieren einfach eine von der anderen. Für weitere Details können Sie sich Cross-Entropy und Kullback-Leibler-Divergenz ansehen.
Aber beachten Sie, dass dies ein vereinfachtes Beispiel ist. Realistischerweise werden wir einen Satz verwenden, der länger als ein Wort ist. Zum Beispiel - Eingabe: “je suis étudiant” und erwartete Ausgabe: “i am a student”. Was das wirklich bedeutet, ist, dass wir möchten, dass unser Modell sukzessive Wahrscheinlichkeitsverteilungen ausgibt, bei denen:
- Jede Wahrscheinlichkeitsverteilung durch einen Vektor der Breite vocab_size (6 in unserem Beispiel, aber realistischerweise eine Zahl wie 30.000 oder 50.000) repräsentiert wird.
- Die erste Wahrscheinlichkeitsverteilung die höchste Wahrscheinlichkeit in der Zelle aufweist, die mit dem Wort “i” verbunden ist.
- Die zweite Wahrscheinlichkeitsverteilung die höchste Wahrscheinlichkeit in der Zelle aufweist, die mit dem Wort “am” verbunden ist.
- Und so weiter, bis die fünfte Ausgangsverteilung das Symbol
<end of sentence>anzeigt, das ebenfalls eine zugehörige Zelle aus dem Vokabular mit 10.000 Elementen hat.
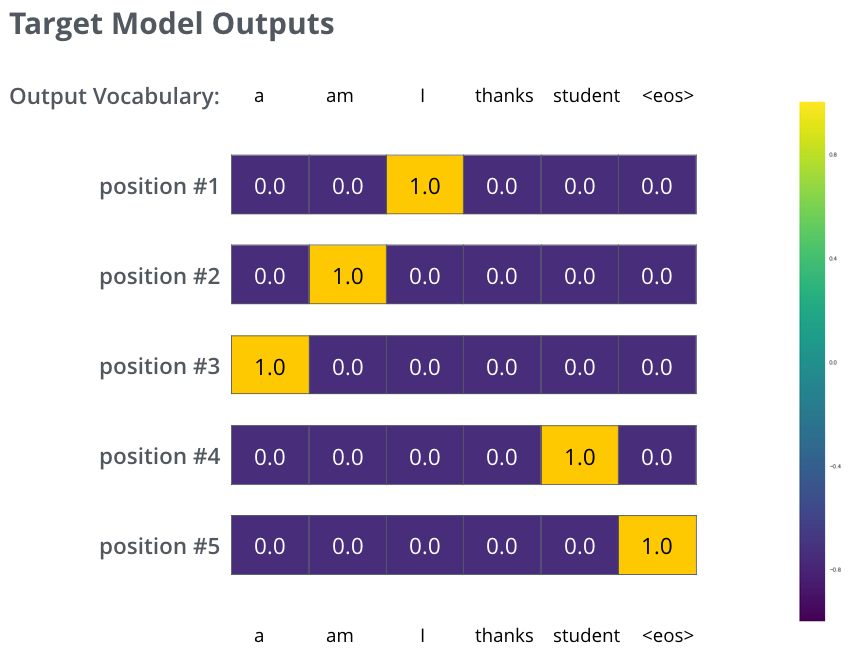
Nachdem das Modell ausreichend lange auf einem ausreichend großen Datensatz trainiert wurde, würden wir hoffen, dass die produzierten Wahrscheinlichkeitsverteilungen folgendermaßen aussehen würden:
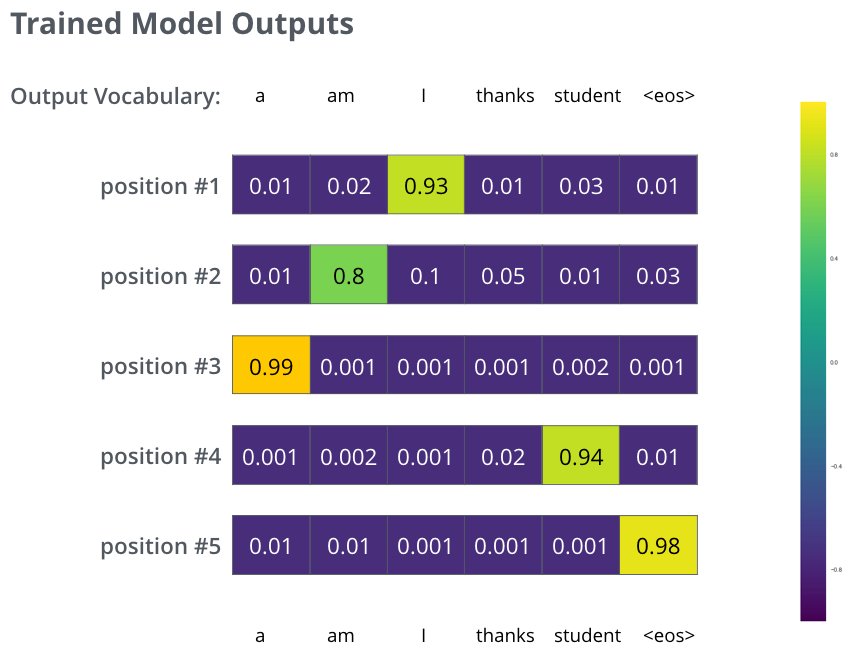
Da das Modell die Ausgaben nacheinander produziert, können wir davon ausgehen, dass das Modell das Wort mit der höchsten Wahrscheinlichkeit aus dieser Wahrscheinlichkeitsverteilung auswählt und den Rest verwirft. Das ist eine Möglichkeit (genannt Greedy-Decodierung). Eine andere Möglichkeit wäre es, zum Beispiel die beiden besten Wörter (sagen wir ‘I’ und ‘a’ zum Beispiel) zu behalten, und im nächsten Schritt das Modell zweimal auszuführen: einmal unter der Annahme, dass die erste Ausgabeposition das Wort ‘I’ war, und ein weiteres Mal unter der Annahme, dass die erste Ausgabeposition das Wort ‘a’ war, und die Version, die bei Berücksichtigung beider Positionen #1 und #2 weniger Fehler produziert, wird beibehalten. Dies wiederholen wir für Positionen #2 und #3 usw. Diese Methode wird als “Beam Search” bezeichnet, wobei in unserem Beispiel beam_size zwei beträgt (was bedeutet, dass zu jedem Zeitpunkt zwei unvollständige Hypothesen (unvollständige Übersetzungen) im Speicher gehalten werden), und top_beams ebenfalls zwei beträgt (was bedeutet, dass wir zwei Übersetzungen zurückgeben werden). Dies sind beides Hyperparameter, mit denen Sie experimentieren können.
D.6 Geh weiter und transformiere!
Ich hoffe, du hast dies als nützlichen Einstieg in die wichtigsten Konzepte des Transformers empfunden. Wenn du tiefer einsteigen möchtest, würde ich diese nächsten Schritte empfehlen:
- Lies das Paper Attention Is All You Need, den Blog-Beitrag Transformer: A Novel Neural Network Architecture for Language Understanding und die Ankündigung von Tensor2Tensor.
- Schau dir den Vortrag von Łukasz Kaiser an, der das Modell und seine Details erläutert.
- Spiele mit dem Jupyter-Notebook, das als Teil des Tensor2Tensor-Repositorys bereitgestellt wird.
- Erkunde das Tensor2Tensor-Repository.
D.6.1 Danksagungen
Vielen Dank an Illia Polosukhin, Jakob Uszkoreit, Llion Jones, Lukasz Kaiser, Niki Parmar und Noam Shazeer für ihr Feedback zu früheren Versionen dieses Beitrags.
Kontaktieren Sie Jay Alammar auf Twitter für Korrekturen oder Feedback.
Geschrieben am 1. Juni 2018.
D.7 Lizenz dieser Übersetzung

Übersetzung durch Michael Kipp, April 2024. Diese Übersetzung läuft - wie auch der Originalartikel - unter der Creative-Commons-Lizenz CC BY-NC-SA 4.0. Bei Referenzen bitte den Linik zu dieser Seite angeben: https://michaelkipp.de/deeplearning/Transformer-illustriert.html