from tensorflow.keras.datasets import cifar10
from tensorflow.keras.utils import to_categorical
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
x_train = x_train / 255.0
x_test = x_test / 255.0
y_train = to_categorical(y_train, 10)
y_test = to_categorical(y_test, 10)9 Trainingstechniken
Nachdem wir die Grundmechanismen von Konvolutionsnetzen kennengelernt haben, sehen wir uns hier einige praktische Aspekte für das Training an. Zunächst sehen wir Regularisierungsmethoden wie Weight Decay und lernen, wie man die Lernrate dynamisch anpassen kann. Wir lernen ferner Methoden kennen, um den Effekt von Overfitting abzuschwächen: Data Augmentation, Dropout, Batch Normalization und Layer Normalization.
Konzepte in diesem Kapitel
Data Augmentation, Regularisierung, Dropout, Batch Normalization, Layer Normalization, LearningRateScheduler
Lernziele, um Ihren Lernfortschritt zu prüfen
- Sie können Data Augmentation als Methode erklären und praktisch in Keras anwenden
- Sie können Regularisierung in Keras anwenden
- Sie verstehen die Methode Dropout zur Verbesserung der Generalisierung von Modellen und können Dropout in Keras anwenden
- Sie verstehen die Funktionsweise von Batch Normalization und können die Methode erklären und in Keras anwenden
- Sie können die Lernrate in Keras dynamisch anpassen und wissen, warum das sinnvoll sein kann
9.1 Data Augmentation
Das Problem des Overfittings besteht darin, dass ein Modell sich zu stark an die Trainingsdaten anpasst. So werden bestimmte Eigenarten eines Trainingsbildes zu bestimmenden Faktoren bei der Klassifikation. Klar ist, dass eine größere Menge an Daten immer hilft und daher ist eine Idee, die Menge der Trainingsdaten künstlich zu erhöhen, indem man systematisch Varianten von jedem Trainingsbeispiel herstellt.
Bei Bildern kommen zum Beispiel folgende Manipulationen in Frage, um Varianten herzustellen:
- Verschiebung
- Drehung
- Skalierung (Vergrößern, Verkleinern)
- Verzerrung (z.B. Scherung oder nur entlang einer Achse vergrößern)
- Spiegelung
Diese Operationen können einzeln oder in Kombination angewandt werden, in der Regel mit zufälligen Parametern (z.B. Drehwinkel oder Verschiebungsvektor).
Zu beachten ist, dass die Bildgröße dabei gleich bleiben muss. Bei einigen Operationen wie Drehung oder Scherung entstehen “Lücken” im Bild, die entsprechend einer Systematik aufgefüllt werden müssen, z.B. indem man die nächsten Randpixel einfach kopiert.
Die folgende Abbildung zeigt ein Originalbild (links oben) und entsprechende Varianten.
Data Augmentation wurde u.a. bei den Netzen LeNet-5 und AlexNet eingesetzt.
9.1.1 Data Augmentation in Keras
In Keras stehen Ihnen Mechanismen zur Verfügung, um Data Augmentation relativ leicht einzusetzen.
Eine Möglichkeit ist, Data Augmentation direkt in das Modell, also in das Neuronale Netz, als Vorverarbeitungs-Schicht einzubauen. Keras bietet dazu Preprocessing-Schichten an, die eine Vorverarbeitung wie Skalierung im Prozess der Forward Propagation einbauen. In diesem Fall findet also die Variantenbildung im Netz selbst statt (natürlich nur beim Training). Siehe dazu ein TensorFlow-Tutorial zu Data Augmentation
Die zweite (und üblichere) Möglichkeit ist die Variantenbildung während der Bereitstellung der Trainingsdaten. Die Bereitstellung der Daten findet im Training statt und dort werden dann auch die Varianten gebildet. Die Klasse ImageDataGenerator stellt beim Training die Trainingsbeispiele bereit (als Batches) und nimmt die Variantenbildung automatisiert vor. Man kann dort verschiedene Operationen mit entsprechenden Grenzwerten (z.B. für den Drehwinkel) definieren und beim Training werden dann die Varianten on-the-fly gebildet. Siehe auch Keras Image data loading
9.1.2 Beispiel mit ImageDataGenerator (CIFAR-10)
Wir sehen uns Data Augmentation am Beispiel von CIFAR-10 an (Abschnitt 7.3.2). Dabei lernen wir gleich, wie ImageDataGenerator funktioniert.
Wir laden die Daten, normalisieren die Werte und erzeugen One-Hot-Vektoren.
Hier erzeugen wir eine Instanz von ImageDataGenerator. Dabei geben wir zwei Operationen an:
- seitliche Verschiebung um maximal 10%
- horizontale Spiegelung
Es handelt sich also um sehr kleine Änderungen.
from keras.preprocessing.image import ImageDataGenerator
datagen = ImageDataGenerator(
width_shift_range=0.1,
horizontal_flip=True)
datagen.fit(x_train)Wir erzeugen das gleiche CNN wie in Abschnitt 8.7.5, wo wir ca. 66% bei den Testdaten von CIFAR-10 erreicht haben.
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten, Conv2D, MaxPool2D
model = Sequential()
model.add(Conv2D(filters=10,
kernel_size=5,
activation='relu',
padding='same',
input_shape=x_train[0].shape))
model.add(MaxPool2D(pool_size=2)) # stride ist somit 2
model.add(Conv2D(filters=20,
kernel_size=3,
activation='relu',
padding='same'))
model.add(MaxPool2D(pool_size=2)) # stride ist somit 2
model.add(Flatten())
model.add(Dense(200, activation='relu'))
model.add(Dense(10, activation='softmax'))
model.summary()Model: "sequential_8"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_16 (Conv2D) (None, 32, 32, 10) 760
max_pooling2d_16 (MaxPoolin (None, 16, 16, 10) 0
g2D)
conv2d_17 (Conv2D) (None, 16, 16, 20) 1820
max_pooling2d_17 (MaxPoolin (None, 8, 8, 20) 0
g2D)
flatten_8 (Flatten) (None, 1280) 0
dense_16 (Dense) (None, 200) 256200
dense_17 (Dense) (None, 10) 2010
=================================================================
Total params: 260,790
Trainable params: 260,790
Non-trainable params: 0
_________________________________________________________________Wir nutzen auch die gleichen Trainingseinstellungen.
model.compile(loss='categorical_crossentropy',
optimizer='adam',
metrics=['acc'])Hier sehen wir einen Unterschied zum “normalen” Training. Die Trainingsdaten kommen jetzt von unserem Generator-Objekt über die Funktion flow. Man spezifiziert hier noch steps_per_epoch, aber da wählt man normalerweise die Anzahl der Trainingsdaten geteilt durch die Batchgröße (so machen wir es auch hier).
batch_size = 32
steps_per_epoch = len(x_train) // batch_size
model.fit(datagen.flow(x_train, y_train, batch_size=batch_size),
steps_per_epoch=steps_per_epoch,
epochs=15,
validation_data=(x_test, y_test))Epoch 1/15
1562/1562 [==============================] - 21s 13ms/step - loss: 1.5434 - acc: 0.4439 - val_loss: 1.2707 - val_acc: 0.5417
Epoch 2/15
1562/1562 [==============================] - 16s 10ms/step - loss: 1.2309 - acc: 0.5633 - val_loss: 1.1520 - val_acc: 0.5939
Epoch 3/15
1562/1562 [==============================] - 16s 10ms/step - loss: 1.1105 - acc: 0.6066 - val_loss: 1.0301 - val_acc: 0.6328
Epoch 4/15
1562/1562 [==============================] - 17s 11ms/step - loss: 1.0370 - acc: 0.6331 - val_loss: 0.9940 - val_acc: 0.6500
Epoch 5/15
1562/1562 [==============================] - 19s 12ms/step - loss: 0.9864 - acc: 0.6516 - val_loss: 0.9688 - val_acc: 0.6575
Epoch 6/15
1562/1562 [==============================] - 18s 11ms/step - loss: 0.9384 - acc: 0.6684 - val_loss: 0.9685 - val_acc: 0.6589
Epoch 7/15
1562/1562 [==============================] - 18s 11ms/step - loss: 0.9052 - acc: 0.6830 - val_loss: 0.8881 - val_acc: 0.6918
Epoch 8/15
1562/1562 [==============================] - 18s 12ms/step - loss: 0.8726 - acc: 0.6941 - val_loss: 0.9124 - val_acc: 0.6835
Epoch 9/15
1562/1562 [==============================] - 17s 11ms/step - loss: 0.8459 - acc: 0.7029 - val_loss: 0.9864 - val_acc: 0.6604
Epoch 10/15
1562/1562 [==============================] - 18s 11ms/step - loss: 0.8268 - acc: 0.7099 - val_loss: 0.8767 - val_acc: 0.7018
Epoch 11/15
1562/1562 [==============================] - 18s 11ms/step - loss: 0.8015 - acc: 0.7182 - val_loss: 0.8580 - val_acc: 0.7046
Epoch 12/15
1562/1562 [==============================] - 18s 11ms/step - loss: 0.7847 - acc: 0.7237 - val_loss: 0.8711 - val_acc: 0.7024
Epoch 13/15
1562/1562 [==============================] - 16s 10ms/step - loss: 0.7724 - acc: 0.7306 - val_loss: 0.8479 - val_acc: 0.7092
Epoch 14/15
1562/1562 [==============================] - 16s 10ms/step - loss: 0.7509 - acc: 0.7356 - val_loss: 0.8609 - val_acc: 0.7081
Epoch 15/15
1562/1562 [==============================] - 16s 10ms/step - loss: 0.7337 - acc: 0.7405 - val_loss: 0.8280 - val_acc: 0.7184<keras.callbacks.History at 0x7f9249334c40>loss, acc = model.evaluate(x_test, y_test, verbose=0)
print(f"\n++++++++++++ Test Data Accuracy = {acc:.4f} ++++++++++++")
++++++++++++ Test Data Accuracy = 0.7184 ++++++++++++Sie sehen einen sehr deutlichen Zugewinn zu den 66%, obwohl wir nur sehr zart die Daten verändert haben. Nur als Vorwarnung: Ein zu aggressives Augmentieren wird schnell kontraproduktiv.
9.2 Regularisierung und Weight Decay
Regularisierung bedeutet, dass hohe Gewicht ganz allgemein “bestraft” werden. So wird erreicht, dass keine zu großen Unterschiede unter den Gewichten entstehen und so soll Overfitting vermieden werden. Wir haben L2-Regularisierung in Abschnitt 5.2.2 als Teil der Fehlerfunktion kennen gelernt. Wenn in einer Publikation von weight decay gesprochen wird, ist damit Regularisierung gemeint.
In Keras kann man L1- oder L2-Regularisierung verwenden oder beides gleichzeitig. Die relevanten Klassen finden sich im Paket keras.regularizers:
- l1
- l2
- l1_l2 (verwendet sowohl L1 als auch L2)
Man kann auch eigene Regularisierer über eine Funktion und eine Unterklasse von Regularizer definieren.
Die Regularisierung für jede Schicht spezifiziert. Man kann einen String Identifier übergeben:
layer = Dense(30, kernel_regularizer='l2')Alternativ als Objekt, dann kann man den Regularisierungsfaktor (bei uns \(\lambda\)) angeben:
layer = Dense(30, kernel_regularizer=l2(l2=0.01))Bei l1_l2 hat man zwei Argumente:
layer = Dense(30, kernel_regularizer=l1_l2(l1=0.01, l2=0.01))Neben kernel_regularizer gibt es noch
- bias_regularizer: Regularizer to apply a penalty on the layer’s bias
- activity_regularizer: Regularizer to apply a penalty on the layer’s output
Siehe auch die Keras-Doku zu Regularizers sowie den Artikel Keras Weight Decay Hack.
9.3 Dropout
Dropout ist eine sehr effektive Methode gegen Overfitting aus der Arbeitsgruppe von Geoffrey Hinton (University of Toronto) mit der Idee, ein Netz in jedem Batch-Durchlauf nur mit einer zufälligen Teilmenge der Neuronen zu trainieren (Hinton et al. 2012; Srivastava et al. 2014).
Ein Gedanke dahinter ist, dass ein einzelnes Neuron so lernen muss, in verschiedenen Kontexten zu arbeiten, weil mal dieses Nachbarneuron ausfällt und mal jenes. Es kann sich also nicht darauf verlassen, mit einem ganz bestimmten Neuron eine klare Aufgabenteilung einzurichten (das nennt man auch co-adaptation, daher das preventing co-adaptation im Titel von Hinton et al. 2012). Umgekehrt heißt das, die Fähigkeit zur Generalisierung bzw. zur Zusammenarbeit mit vielen andern Neuronen, wird gestärkt.
9.3.1 Methode
Jedes Neuron wird mit einer bestimmten Wahrscheinlichkeit ein- oder ausgeschaltet. Wir nehmen \(p\) als Wahrscheinlichkeit, dass ein Neuron aktiv ist. Wenn z.B. \(p = 0.5\) ist, dann ist im Mittel immer nur die Hälfte des Netzwerks aktiv, d.h. das Netz ist ausgedünnt.
Hier sehen wir ein Beispiel:
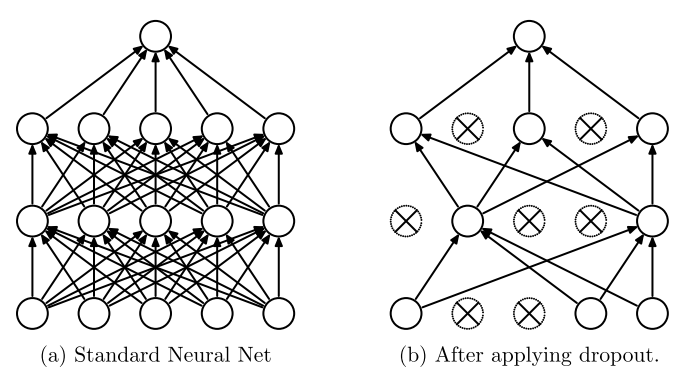
In jedem Trainingsdurchlauf wird das ausgedünnte Netz erst neu bestimmt und dann trainiert. Man kann sich überlegen, dass es bei \(n\) Neuronen \(2^n\) verschiedene Varianten von ausgedünnten Netzen gibt. Man kann sich also vorstellen, dass \(2^n\) verschiedene Netze gleichzeitig trainiert werden und sich dabei die Gewichte teilen.
In unseren Formeln für Forward Propagation haben wir folgende Formel für die Aktivierungen:
\[ a^{(l)} = g(z^{(l)}) = \left( \begin{array}{c} g(z_1^{(l)}) \\ \vdots \\ g(z_{n_l}^{(l)}) \end{array} \right)\]
Hier würden wir einen Bernoulli-Vektor \(B(p)\) einbauen, der Nullen und Einsen mit der Wahrscheinlichkeitsverteilung \(p\) (für die Einsen) enthält. Ein Beispiel für einen Bernoulli-Vektor mit \(p=0.75\) wäre
\[ B(0.75) = \begin{pmatrix} 1 \\ 1 \\ 0 \\ 1 \end{pmatrix} \]
Dann können wir die Aktivierung \(\tilde{a}\) unseres ausgedünnten Netzes schreiben als:
\[ \tilde{a}^{(l)} = B(p) \odot \left( \begin{array}{c} g(z_1^{(l)}) \\ \vdots \\ g(z_{n_l}^{(l)}) \end{array} \right)\]
Dabei ist \(\odot\) die elementweise Multiplikation, d.h. es werden ganz einfach einige der Komponenten des rechten Vektors “ausgeschaltet” (= auf Null gesetzt).
Backpropagation
Beim Training wird für jeden Minibatch-Durchlauf eine Konfiguration über die Bernoulli-Vektoren hergestellt und Backpropagation wird genau auf diesem ausgedünnten Netz durchgeführt. Das heißt, es werden bei Backpropagation nur die Gewichte zwischen den “aktiven” Neuronen angepasst.
Methoden wie Momentum und Decay können auch zusammen mit Dropout angewendet werden.
Vorhersagen
Beim Testen - oder allgemein beim Berechnen einer Vorhersage - können für eine Eingabe nicht alle \(2^n\) möglichen Netze durchlaufen werden. Stattdessen wird das vollständige Netz genommen und jedes Gewicht mit dem Faktor \(p\) multipliziert, also effektiv runterskaliert. Das ist notwendig, weil beim Training die Rohinputs eine um \(p\) reduzierte “Masse” an Eingaben der vorigen Schicht bekommen haben (also zum Beispiel nur die Hälfte bei \(p=0.5\)).
In unseren Formeln für Forward Propagation müsste \(p\) also beim Rohinput eingebaut werden, zum Beispiel so:
\[ z_i^{(l)} = p \, \sum_{j=1}^{n_{l-1}} w^{(l-1)}_{i,j} \; a_j^{(l-1)} + b_i^{(l-1)} \]
Wie schon erwähnt brauchen wir dies, weil im Training weniger Neuronen/Gewichte aktiv waren und beim vollständigen Netz sonst viel mehr Aktivierung aufkommt als im Training. Bei \(p=0.75\) sind nur 75% aller Neuronen im Training aktiv gewesen, also reduzieren wir die Aktivität bei der Vorhersage um 25%.
9.3.2 In Keras
In Keras kann man Dropout an bestimmte Schichten hängen. Dropout wird als eigene Schicht umgesetzt - eine sogenannte Regularisierungsschicht. Für jede Dropout-Schicht legt man den Wert \(p\) fest.
Wichtig ist, dass im Gegensatz zur obigen Darstellung das \(p\) bei Keras bestimmt, mit welcher Wahrscheinlichkeit Neuronen deaktiviert werden. Das heißt bei \(p=0.25\) sind 75% der Neuronen aktiv.
Hier ein Beispielnetz mit Dropout an zwei Stellen (jeweils \(p=0.25\)):
model = Sequential()
model.add(Conv2D(filters=30,
kernel_size=5,
activation='relu',
padding='same',
input_shape=x_train[0].shape))
model.add(MaxPool2D(pool_size=2))
...
model.add(MaxPool2D(pool_size=2, strides=2))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(200, activation='relu'))
model.add(Dropout(0.25))
model.add(Dense(10, activation='softmax'))Siehe Keras zu Dropout
Einsatz und p-Wert
Dropout wird ausschließlich zwischen FC-Schichten eingesetzt, um dort die Dichte und effektive Parameterzahl zu reduzieren. Dies ist bei Konvolutionsschichten nicht sinnvoll, da wir dort eine reduzierte Parameterzahl haben, die auch mehrfach angewendet werden.
Dropout reduziert Overfitting, führt aber auch zu einer längeren Trainingszeit. In AlexNet wird Dropout zwischen zwei FC-Schichten eingesetzt und Krizhevsky et al. (2014) sagen dazu: “Without dropout, our network exhibits substantial overfitting. Dropout roughly doubles the number of iterations required to converge.”
Welchen Wert wählt man für \(p\)? Wir sehen hier \(p\) im Sinne von Keras, also für den Anteil der deaktivierten Neuronen. Hinten et al. (2012) haben Dropout mit \(p=0.5\) eingeführt und dieser Wert wird auch in Srivastava et al. (2014) empfohlen. In den beiden Papers werden umfangreiche Experimente mit \(p=0.5\) vorgestellt. In der Praxis sieht man auch Werte unter \(0.5\), zum Beispiel \(p = 0.25\).
9.4 Batch Normalization und Layer Normalization
Batch Normalization (auch Batch norm) ist ein wirkungsvolles Verfahren, um Overfitting abzuschwächen (Ioffe and Szegedy 2015). Man kann es auch als Alternative zu Dropout betrachten. Das Verfahren erlaubt es, höhere Lernraten zu verwenden und damit effizienter zu trainieren.
Wir haben bereits in Abschnitt 3.6.1 gesehen, dass es sinnvoll ist, die Featurevektoren unserer Trainingsdaten zu skalieren, entweder durch Normalisierung auf den Bereich [0, 1] oder durch Standardisierung mit Hilfe von Mittelwert und Varianz. Natürlich ist auch Standardisierung eine Form der Normalisierung.
Die Grundidee von Batch Normalization ist es nun, etwas ähnliches für die Rohinputs jeder Schicht zu tun. Das heißt zum Beispiel für Schicht \(l\), dass wir alle berechneten Rohinputs \(z^{(l)}_1, \ldots, z^{(l)}_{n_l}\) nehmen und zunächst skalieren, bevor sie über die Aktivierungsfunktion in die nächste Schicht \(l+1\) gehen, so dass die weitere Verarbeitung, d.h. das Lernen der Gewichte, schneller und kontrollierter vonstatten geht.
Man skaliert an jedem Neuron einer Schicht den Rohinput \(z^{(l)}_i\) mit Hilfe von des Mittelwerts und der Varianz aller Rohinput-Werte dieses Neurons über alle Trainingsbeispiele hinweg (in der Theorie). In der Praxis werden Mittelwert und Varianz “nur” auf den Trainingsbeispielen eines Batches berechnet und nicht auf dem gesamten Trainingsdatensatz.
Wichtig ist außerdem, dass zwei neue zu lernende Parameter für jedes Neuron hinzukommen: Gamma \(\gamma\) für eine Skalierung und Beta \(\beta\) für eine Verschiebung. Durch den Parameter \(\beta\) wird das Bias-Neuron der dazugehörigen Schicht überflüssig, so dass bei Anwendung von Batch Normalization die Bias-Gewichte in der Regel weggelassen werden. Die Parameter \(\gamma\) und \(\beta\) werden angelernt, d.h. sie werden per Gradientenabstieg im Zuge des Backpropagation optimiert.
Layer Normalization ist ähnlich zu Batch norm mit dem Unterschied, dass nicht über alle Beispiele eines Batches normalisiert wird, sondern über alle Neuronen einer Schicht (Lei Ba, Kiros, and Hinton 2016). Layer Normalization wurde als Modifikation von Batch Normalization für Rekurrente Netze entwickelt und kommt auch bei Transformern zum Einsatz (Vaswani et al. 2017).
Ein schöner Artikel zum Thema: Build Better Deep Learning Models with Batch and Layer Normalization
9.4.1 Formal
Wie der Name Batch norm schon andeutet, wird die Normalisierung über einen Batch vorgenommen, also einer Teilmenge der Trainingsdaten. Wir betrachten hier eine einzelne Schicht in einem Neuronalen Netz. Es kann sowohl eine fully connected Schicht sein oder eine Konvolutions-Schicht. In beiden Fällen haben wir Rohinput-Werte, die wie beschrieben verändert werden.
Wir befinden uns ferner bei der Verarbeitung eines Batches. Mit \(m\) bezeichnen wir die Größe des Batches, also die Anzahl der Trainingsbeispiele. Wenn wir die Trainingsbeispiele des Batches durchlaufen haben, liegen \(m\) Rohinput-Vektoren vor, z.B. \(z^1, \ldots, z^{32}\) bei einer beispielhaften Batchgröße von 32. Wir bezeichnen mit \(B\) die Menge der Indizes eines Batches und berechnen zunächst Mittelwert und Varianz für diesen einen Batch:
\[ \begin{align} \mu &= \frac{1}{m} \sum_{k \in B} z^k \\[3mm] \sigma^2 & =\frac{1}{m} \sum_{k \in B} (z^k - \mu)^2 \end{align} \]
Im Grunde berechnet man dies für jede Komponente eines Vektors \(z\) separat, d.h. wir können auch die Komponenten der Vektoren betrachten. Wir nennen \(n\) die Anzahl der Neuronen in der aktuellen Schicht. Dann gilt für \(i \in {1, \ldots, n}\):
\[ \begin{align} \mu_i &= \frac{1}{m} \sum_{k \in B} z_i^k \\[3mm] \sigma_i^2 & =\frac{1}{m} \sum_{k \in B} (z_i^k - \mu_i)^2 \end{align} \]
Jetzt verändern wir die Rohinputs \(z_i^k\) für alle \(k \in B\) und nennen sie \(\hat{z}_i\):
\[ \hat{z}_i^k = \frac{x_i^k - \mu_i}{\sqrt{\sigma_i^2 + \epsilon}} \]
Der endgültige neue Wert \(\bar{z}_i^k\) wird noch einmal mit Faktor \(\gamma_i\) skaliert und um Wert \(\beta_i\) verschoben.
\[ \bar{z}_i^k = \gamma_i \cdot \hat{z}_i^k + \beta_i \]
Bei der Forward Propagation werden nach Verarbeitung eines Batch alle Aktivierungen \(z\) durch \(\bar{z}\) ausgetauscht. Im Lernschritt werden auch die \(\gamma_i\) und die \(\beta_i\) mit Hilfe von Gradientenabstieg angepasst (siehe z.B. Abschnitt 6.7).
Bei Layer Normalization verläuft die Berechnung von Mittelwert und Varianz in einer gegebenen Schicht wie folgt:
\[ \begin{align} \mu &= \frac{1}{n} \sum_{i=1}^n z_i \\[3mm] \sigma^2 & =\frac{1}{n} \sum_{i=1}^n (z_i - \mu)^2 \end{align} \]
Wir normalisieren also über alle Neuronen dieser Schicht und zwar für jedes Trainingsbeispiel. Es ist somit unabhängig von der Batch-Größe und auch anwendbar für Rekurrente Netze.
9.4.2 In Keras
Siehe die Keras-Doku zu Batch Normalization
Wir folgen den Empfehlungen des Artikels One simple trick to train Keras model faster with Batch Normalization und vergleichen immer eine “normale” Schicht mit einer Schicht, die mit Batch Normalization versehen wird.
Wir benötigen folgende Imports:
from tensorflow.keras.layers import Dense, Conv2D, BatchNormalization, ActivationFC-Schichten
Normalerweise definieren wir eine FC-Schicht etwa so:
model.add(Dense(64, activation='relu'))Mit Batch Normalization wird dies zu:
model.add(Dense(64, use_bias=False))
model.add(BatchNormalization())
model.add(Activation("relu"))Wir benötigen kein Bias-Neuron, dass der Parameter \(\beta\) diese Funktion mit abdeckt.
Konvolutionsschicht
Normalerweise definieren wir eine Konv-Schicht so:
model.add(Conv2D(64, (3, 3), activation='relu'))Mit Batch Normalization:
model.add(Conv2D(64, (3, 3), use_bias=False))
model.add(BatchNormalization())
model.add(Activation("relu"))9.4.3 Alternative Erklärungen
Andrews Ng beschreibt Batch Normalization in den folgenden drei Videos:
- Normalizing Activations in a Network
- Fitting Batch Norm into a Neural Network
- Why does Batch Norm work?
Der Artikel Batch Norm Explained Visually — How it works, and why neural networks need it kann auch hilfreich sein.
9.5 Lernrate dynamisch anpassen
Die Lernrate bestimmt, wie schnell sich die Gewichte anpassen. Wählt man einen relativ großen Wert wie 0.1, dann spart man Trainingszeit, aber erwischt eventuell nicht den optimalen Punkt. Oft möchte man mit einer hohen Lernrate wie 0.1 oder 0.01 beginnen und später die Lernrate reduzieren, z.B. nach ein bestimmten Anzahl von Epochen um den Faktor 10 verkleinern. Die Idee ist, dass man sich in der Fehlerlandschaft erst schnell dem Minimum nähert und in der Nähe des Minimums langsamer wird, um nicht um das Minimum herum zu oszillieren.
Funktion zur Anpassung der Lernrate
In Keras definiert man zunächst eine eigene Funktion mit zwei Parametern. Der erste Parameter ist die aktuelle Epochenzahl, der zweite Parameter die aktuelle Lernrate. Die Funktion gibt die neue gewünschte Lernrate zurück.
Hier ein Beispiel, wo die Lernrate bei Epoche 10, 15, 20 … um jeweils Faktor 10 veringert wird (also z.B. 0.1, 0.01, 0.001…)
def scheduler(epoch, lr):
if epoch >= 10 and epoch%5 == 0:
return lr/10.0
else:
return lrÜberwachungsobjekt
Die obige Funktion wird in ein Objekt des Typs LearningRateScheduler gepackt. Als zweites Argument kann man einen Wert für verbose angeben (0: ohne Meldungen, 1: mit Meldungen).
Sie müssen dazu den LearningRateScheduler importiert haben:
from keras.callbacks import LearningRateSchedulerAnschließend kann man es für das Training mit fit der Liste von Callback-Funktion hinzufügen. Hier mit verbose=1:
model.fit(..., callbacks=[LearningRateScheduler(scheduler, 1)])Siehe auch die Keras-Doku zu LearningRateScheduler.