import tensorflow
import math
from math import exp
import matplotlib.pyplot as plt
import numpy as np
import time4 Feedforward-Netze
In diesem Kapitel verallgemeinern wir das Perzeptron und betrachten Netze mit mehreren Schichten, sogenannte Feedforward-Neuronale-Netze (FNN). Die Ausgabeschicht besteht in der Regel aus mehreren Neuronen, um eine Mehrklassen-Klassifikation vornehmen zu können (im Vergleich zur binären Klassifikation mit einem Ausgabeneuron). Zum Lernen der Parameter stellen wir das Verfahren Backpropagation vor, vielleicht das wichtigste Verfahren im Bereich neuronaler Netze.
Konzepte in diesem Kapitel
Forward Propagation, Gewichte und Gewichtsmatrix, Schichten, One-Hot-Encoding, Aktivierungsfunktion, Softmax, Bias-Neuronen, Regularisierung, Binary Cross-Entropy, Categorical Cross-Entropy, Backpropagation
Lernziele, um Ihren Lernfortschritt zu prüfen
Nach Abschluss des Kapitels können Sie
- die grundlegenden Konzepte von Feedforward-Netzen (FNN) mathematisch erklären
- die Notation für FNN und den Informationsfluss im Netzwerk (Forward Propagation) anhand der Formeln in Komponenten- und Vektor/Matrixform erklären
- verschiedene Aktivierungsfunktionen nennen
- Backpropagation und Gradientenabstieg erklären sowie relevante Konzepte wie Zielfunktion, Regularisierung und Gradient; insbesondere verstehen Sie die Gewichtsanpassung und können Sie mit konkreten Werten berechnen
- die parallele Verarbeitung mehrerer Trainingsbeispiele bei Backpropagaion als Matrix erklären und die Vorteile begründen
Datensatz
Iris-Datensatz: Abschnitt 3.4.1
| Name | Daten | Anz. Klassen | Klassen | Trainings-/Testdaten | Ort |
|---|---|---|---|---|---|
| MNIST | s/w-Bilder (28x28) | 10 | handgeschriebene Ziffern 0…9 | 60000/10000 | 5.4 |
Importe
Notation
In diesem Kapitel werden wir folgende Notation verwenden.
| Symbol | Bedeutung |
|---|---|
| \(n\) | Anzahl der Eingabeneuronen |
| \(m\) | Anzahl der Ausgabeneuronen |
| \(L\) | Anzahl der Schichten |
| \(n_l\) | Anzahl der Neuronen in Schicht \(l\) |
| \(N\) | Anzahl der Trainingsbeispiele |
| \((x^k, y^k)\) | \(k\)-tes Trainingsbeispiel mit Featurevektor \(x^k\) und korrektem Output \(y^k\) (auch: Label, Klasse) |
| \(X\) | Matrix der Featurevektoren aller Trainingsbeispiele |
| \(W^{(l)}\) | Gewichtsmatrix von Schicht \(l-1\) zu Schicht \(l\) |
| \(b^{(l)}\) | Vektor der Bias-Gewichte von Schicht \(l-1\) zu Schicht \(l\) |
| \(z^{(l)}\) | Rohinput (Vektor) der Neuronen in Schicht \(l\) |
| \(g\) | Aktivierungsfunktion |
| \(a^{(l)}\) | Aktivierung (Vektor) der Neuronen in Schicht \(l\) |
| \(\hat{y}\) | Berechnete Ausgabe (Vorhersage) des Netzwerks bei einer Eingabe \(x\) mit den aktuellen Gewichten |
| \(J\) | Zielfunktion in Form einer Fehler- oder Kostenfunktion (loss function), die es zu minimieren gilt |
| \(\lambda\) | Regularisierungsparameter (kommt in \(J\) zum Einsatz) |
| \(\delta^{(l)}\) | Fehlerwerte (Vektor) an den Neuronen in Schicht \(l\) |
| \(\Delta w^{(l)}_{i,j}\) | Änderungswert von Gewicht \(w_{i,j}\) in Schicht \(l\) und Einzelwert der Matrix \(\Delta W^{(l)}\) |
| \(\Delta b^{l}_i\) | Änderungswert von Bias-Gewicht \(b_i\) in Schicht \(l\) und Einzelwert des Vektors \(\Delta b^{(l)}\) |
| \(\alpha\) | Lernrate \(\in [0, 1]\) |
| \(\beta\) | Momentum-Parameter \(\in [0, 1]\) |
Importe
4.1 Was sind Feedforward-Netze?
Wir gehen über zu Netzwerken, die im Gegensatz zum Perzeptron zusätzliche Schichten zwischen Input- und Outputschicht haben. Diese werden auch versteckte Schichten oder hidden layers genannt. Man kann solche Netze als Feedforward Neural Nets (FNNs) oder als Multilayer Perceptrons (MLP) bezeichnen. Wir werden hier das Kürzel FNN verwenden.
Feedforward-Netze bestehen aus Neuronen und gerichteten Verbindungen. Sie sind also gerichtete azyklische Graphen (directed acyclic graph = DAG), dürfen also keine Zyklen enthalten. Keine Zyklen bedeutet, dass es kein Neuron gibt, von dem aus man über Verbindungen wieder zum selben Neuron gelangen kann.
Zusätzlich sind die Neuronen in geordneten Schichten organisiert. Das bedeutet, dass jede Schicht eine Indexzahl \(l\) besitzt und jedes Neuron in Schicht \(l\) nur Verbindungen zu Neuronen in Schicht \(l+1\) haben darf.
4.1.1 Notation für FNN
Beispielnetz
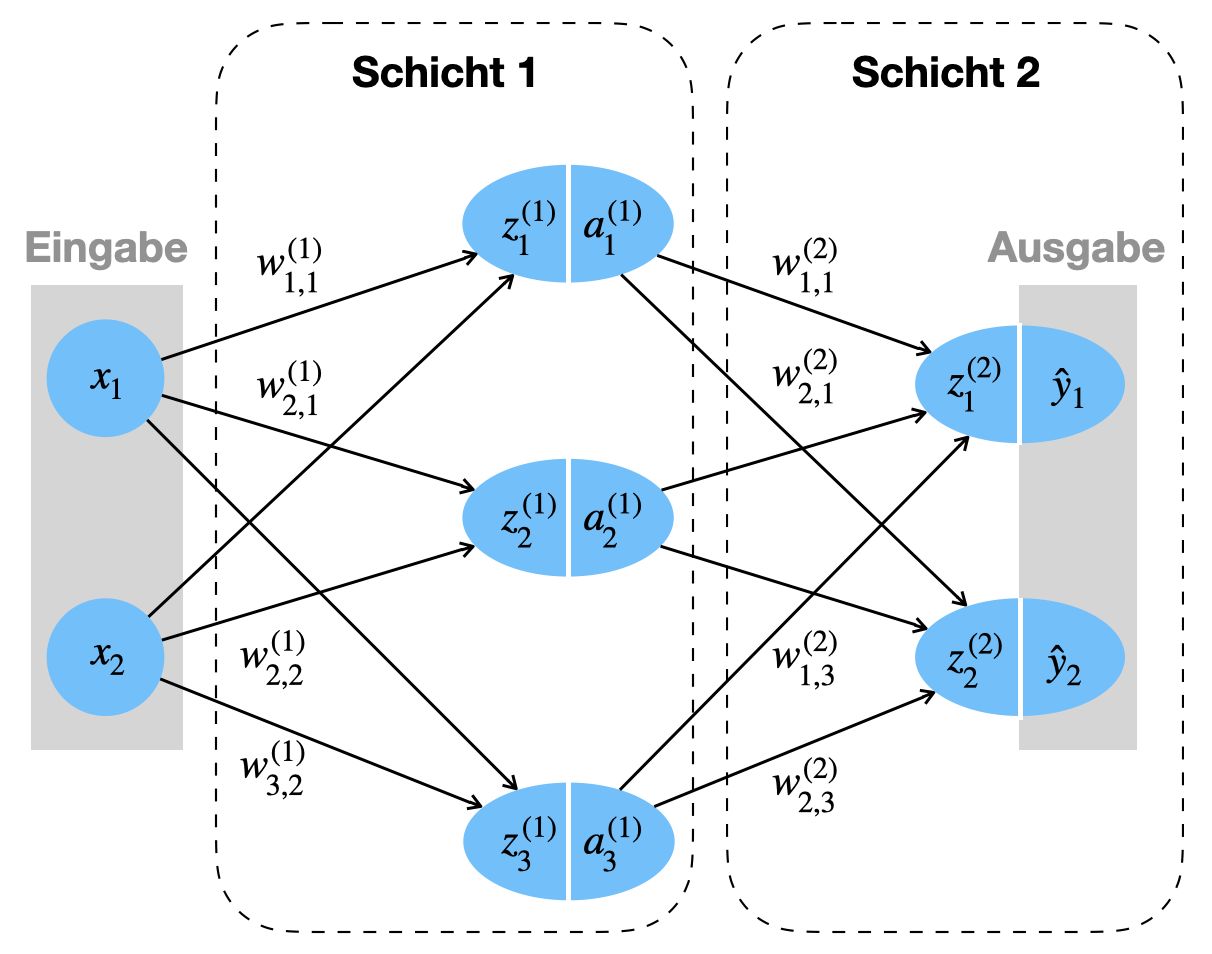
Als durchgängiges Beispiel betrachten wir das Netzwerk in Abbildung 4.1.
Dieses Netz hat:
- eine Eingabe: obwohl man dies als Schicht auffassen könnte, wird die Eingabe nicht als Schicht mitgezählt, da hier noch keine Gewichte/Parameter zum Einsatz kommen
- eine versteckte Schicht (engl. hidden layer): dies ist eine Schicht mit Parametern
- die Ausgabeschicht: auch diese Schicht hat Parameter, die Aktivierung ist gleichzeitig die finale Ausgabe des Netzwerks
Nur parametrisierte Schichten zählen
Ein FNN besteht aus Schichten von Neuronen. Wir unterscheiden zwischen nicht-parametrisierten Schichten (die Eingabeschicht) und parametrisierten Schichten (alle anderen Schichten). Wenn wir von “Schichten” sprechen meinen wir aber die parametrisierten Schichten. Also haben wir es hier mit einem 2-Schicht-Netzwerk zu tun. Diese Zähleweise ist motiviert durch Frameworks wie Keras und PyTorch.
Allgemeine Darstellung
Nachdem wir ein Beispielnetz gesehen haben, betrachten wir in Abbildung 4.2 eine allgemeine Darstellung eines FNN mit \(L\) Schichten.
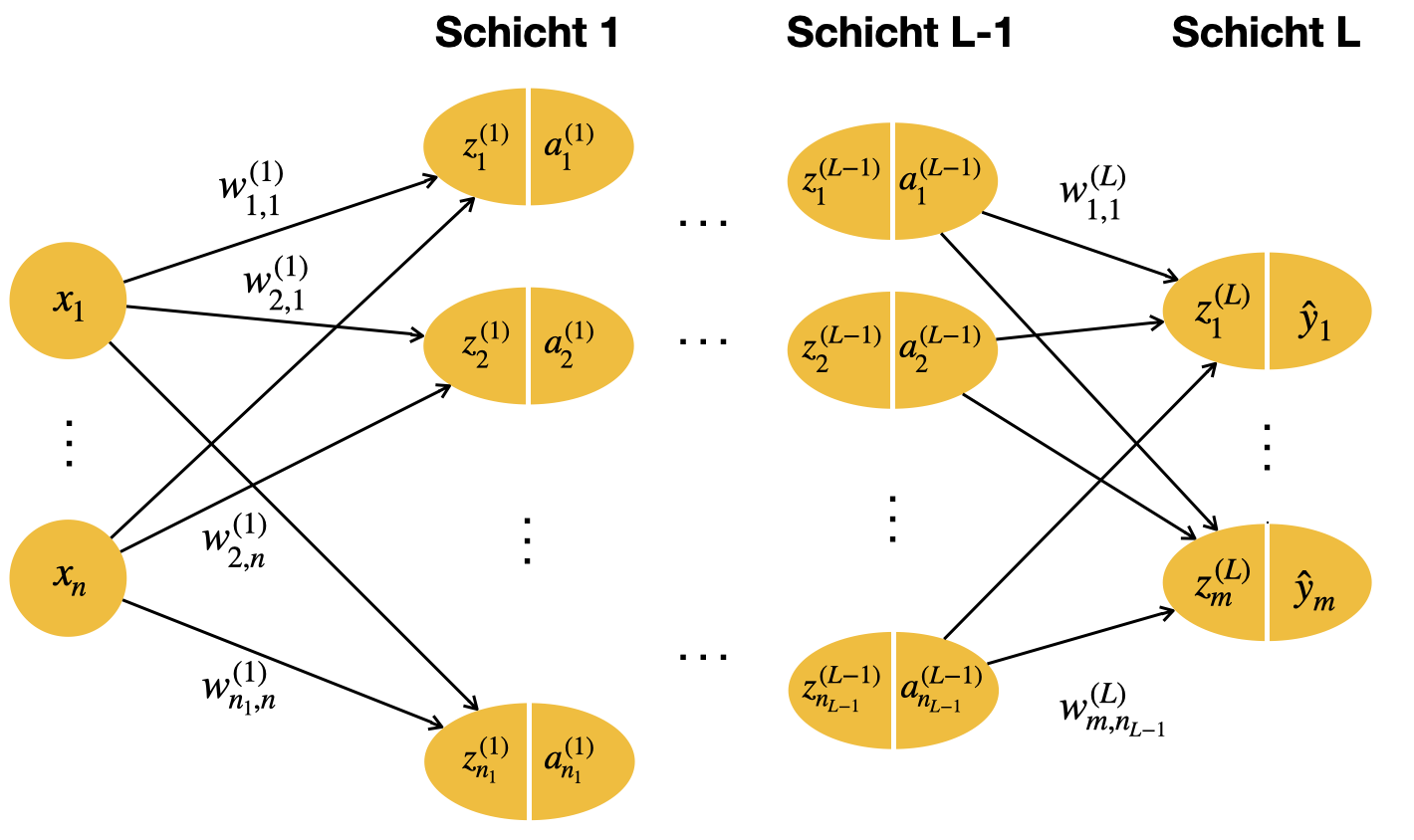
Die Anzahl der (parametrisierten) Schichten nennen wir \(L\). Bei dem Beispielnetz 4.1 wäre \(L = 2\). Wir verwenden Index \(l\), um eine bestimmte Schicht anzuzeigen. Damit wir auch die Neuronen der Eingabeschicht erfassen können, bekommt die Eingabeschicht den Index \(l = 0\). Also ist \(l \in \{0, \ldots, L\}\).
Die Anzahl der Neuronen in Schicht \(l\) wird mit \(n_l\) bezeichnet. Im Beispielnetz 4.1 wären \(n_1 = 3\) und \(n_2 = 2\).
Die Eingabe wird durch einen Vektor der Länge \(n\) repräsentiert:
\[x = (x_1, \ldots, x_n)\]
Die Ausgabe des Netzes wird durch einen Vektor der Länge \(m\) repräsentiert:
\[y = (y_1, \ldots, y_m)\]
Jedes \(y_i\) repräsentiert eine Kategorie bzw. ein Label. Wo die Unterscheidung notwendig ist, bezeichnen wir mit \(y\) die korrekte Ausgabe (eines Trainingsbeispiels) und mit \(\hat{y}\) die berechnete Ausgabe eine Netzwerks mit den aktuellen Gewichten.
Die Roheingabe (net input) des \(i\)-ten Neurons in Schicht \(l\) wird durch \(z_i^{(l)}\) dargestellt.
Die Aktivierung des \(i\)-ten Neurons in Schicht \(l\) wird durch \(a_i^{(l)}\) dargestellt. Den Eingabevektor setzen wir auch mit der Aktivierung von “Schicht 0” gleich:
\[ (x_1, \ldots, x_n) = (a_1^{(0)}, \ldots, a_n^{(0)}) \]
Die Aktivierung der letzten Schicht \(L\) entspricht der berechneten Ausgabe, also
\[ (\hat{y}_1, \ldots, \hat{y}_m) = (a_1^{(L)}, \ldots, a_m^{(L)}) \]
Die Gewichte von Schicht \(l-1\) zu Schicht \(l\) werden als Matrix \(W^{(l)}\) dargestellt. Ein Einzelgewicht von Quellneuron \(i\) in Schicht \(l-1\) zu Zielneuron \(j\) in Schicht \(l\) wird durch \(w_{j,i}^{(l)}\) repräsentiert. Dazu später mehr.
Ausgabe (One-Hot Encoding)
Bislang haben wir nur binäre Klassifikation behandelt. Jetzt möchten wir Klassifizierer betrachten, wo es mehr als zwei Klassen gibt. Die naive Herangehensweise wäre, jede Klasse über eine Zahl (1, 2, 3) zu repräsentieren und mit einem einzigen Ausgabeneuron diese Zahlen zu lernen. Dies ist aber problematisch, weil die Zahlen 1, 2, 3 Zusammenhänge aufweisen, die inhaltlich nicht mit den Klassenzusammenhängen übereinstimmen. Konkret sind die Zahlen 1 und 2 “dichter” beieinander als die Zahlen 1 und 3. Diese Nähe spiegelt sich aber in der Regel nicht in den Kategorien (z.B. Bilderkennung mit 1=Auto 2=Mensch 3=Verkehrsschild). In der Praxis zeigt sich, dass dies den Lernprozess erschwert.
Die Lösung ist, die Klassen derart zu repräsentieren, dass numerisch keine Zusammenhänge abgebildet sind. Bei drei Klassen verwendet man etwas einen Vektor der Länge drei und jede Klasse bekommt eine Komponente, so dass sich drei Zielvektoren für drei Klassen ergeben:
\[ \left( \begin{array}{c} 1 \\ 0\\0 \end{array} \right)\quad \left( \begin{array}{c} 0 \\ 1\\0 \end{array} \right)\quad \left( \begin{array}{c} 0 \\ 0\\1 \end{array} \right) \]
Mathematisch betrachtet handelt es sich um drei Vektoren, die orthogonal zueinander stehen und somit linear unabhängig sind. Man nennt diese Art der Kodierung auch One-Hot Encoding. Es handelt sich um die Standard-Vorgehensweise bei mehreren Klassen (also bei mehr als 2 Klassen).
Man kann jeden Vektor auch als Wahrscheinlichkeitsverteilung sehen, wo die korrekte Klasse mit 1 angegeben ist. Diese Sicht passt zur Softmax-Funktion (siehe Abschnitt 4.1.4).
4.1.2 Forward Propagation
Bei einer konkreten Eingabe \(x\) findet eine Vorwärtsverarbeitung statt, um Ausgabe \(\hat{y}\) zu berechnen (in unseren Abbildungen von links nach rechts). Das nennt man auch Forward Propagation und funktioniert wie beim Perzeptron. Dabei geht man schrittweise durch alle Schichten und berechnet pro Schicht erst Roheingabe und dann Aktivierung der Neuronen. Die Ausgabe \(\hat{y}\) ist die Aktivierung der letzten Schicht \(L\).
Roheingabe
Die Roheingabe für das i-te Neuron in Schicht \(l\) berechnet sich aus der gewichteten Summe der Aktivierungen der vorgeschalteten Schicht \(l-1\).
\[ z_i^{(l)} = \sum_{j=1}^{n_{l-1}} w^{(l)}_{i,j} \; a_j^{(l-1)} \]
wobei \(l \in \{1, \ldots, L\}\) und \(i \in \{1, \ldots, n_l\}\).
Betrachtet man \(z\) als Funktion über die Aktivierungen \(a\) der Vorgängerschicht, handelt es sich um eine lineare Funktion (die Gewichte übernehmen dabei die Rolle von konstanten Koeffizienten).
Hier examplarisch der Rohinput für das erste Neuron der zweiten Schicht (Ausgabeschicht) im Beispielnetz (blau):
\[ \begin{align*} z_1^{(2)} & = \sum_{j=1}^{3} w^{(2)}_{1,j} \; a_j^{(1)} \\[2mm] & = w^{(2)}_{1,1} \; a_1^{(1)} + w^{(2)}_{1,2} \; a_2^{(1)} + w^{(2)}_{1,3} \; a_3^{(1)} \end{align*} \]
Aktivierung
Die Roheingabe \(z\) wird jetzt in die Aktivierungsfunktion \(g\) gegeben, um die Aktivierung des Neurons zu berechnen.
Für ein einzelnes Neuron \(i\) in Schicht \(l\) ist das:
\[ a_i^{(l)} = g(z_i^{(l)}) \]
Als Aktivierungsfunktion für \(g\) wählen wir die Sigmoidfunktion (auch logistische Funktion genannt). Man beachte, dass es sich um eine nicht-lineare Funktion handelt.
\[ g(z) = \frac{1}{1 + e^{-z}} \]
Es sind aber auch andere Aktivierungsfunktionen möglich, siehe Abschnitt 4.1.3.
In der Vektordarstellung werden die Roheingaben für Schicht \(l\) als Vektor \(z^{(l)}\) und die Aktivierungen als Vektor \(a^{(l)}\) dargestellt. Dann können wir die Anwendung der Aktivierungsfunktion wie folgt schreiben:
\[ a^{(l)} = g(z^{(l)}) = \left( \begin{array}{c} g(z_1^{(l)}) \\ \vdots \\ g(z_{n_l}^{(l)}) \end{array} \right)\]
Die Funktion \(g\) wird hier also komponentenweise angewendet.
Output
Die Aktivierung der letzten Schicht \(L\) entspricht dem Gesamtoutput \(\hat{y}\) des FNN.
Für ein einzelnes Ausgabeneuron \(i\) in Schicht \(L\) also:
\[ \hat{y}_i = a_i^{(L)} = g(z_i^{(L)}) \]
In Vektorschreibweise:
\[ \hat{y} = g(z^{(L)}) \]
Matrixdarstellung der Gewichte
Wenn wir die Aktivierungen als Vektoren und die Gewichte als Matrix darstellen, können wir die Formeln wesentlich kompakter darstellen. Wir versuchen, den Übergang möglichst intuitiv zu erklären.
Die Gewichte von Neuronen der Schicht \(l-1\) zu Neuronen der Schicht \(l\) werden als Matrix \(W^{(l)}\) repräsentiert.
Das Einzelgewicht \(w_{j, i}^{(l)}\) ist das Gewicht zwischen Quellneuron \(i\) in Schicht \(l-1\) und dem Zielneuron \(j\) in Schicht \(l\).
Indizes der Gewichtsmatrix
Man beachte die Reihenfolge der Indizes bei der Gewichtsmatrix \(W\): Der erste Index ist das Ziel, zweiter Index die Quelle. Man würde das vielleicht umgekehrt erwarten. Je nach Fachbuch wird auch die umgekehrte Reihenfolge gewählt, dann ändert sich die Multiplikationsreihefolge mit \(W\) in den Gleichungen (siehe auch Hinweis unten).
Für das Beispielnetz sieht die Gewichtsmatrix \(W^{(1)}\) von der Eingabeschicht (Schicht 0) zur versteckten Schicht (Schicht 1) so aus:
\[ \begin{pmatrix} w_{1,1}^{(1)} & w_{1,2}^{(1)} \\ w_{2,1}^{(1)} & w_{2,2}^{(1)} \\ w_{3,1}^{(1)} & w_{3,2}^{(1)} \end{pmatrix} \]
Es handelt sich also um eine 3x2-Matrix. Die Anzahl der Zeilen steht für die Anzahl der Zielneuronen, hier für 3 Neuronen in Schicht 1. Die Anzahl der Spalten steht für die Anzahl der Quellneuronen, hier für 2 Neuronen in Schicht 0 (Eingabe).
Hier sehen wir nochmal den relevanten Teil des Beispielnetzwerks. Vergleichen Sie die Gewichte mit der Matrix oben.
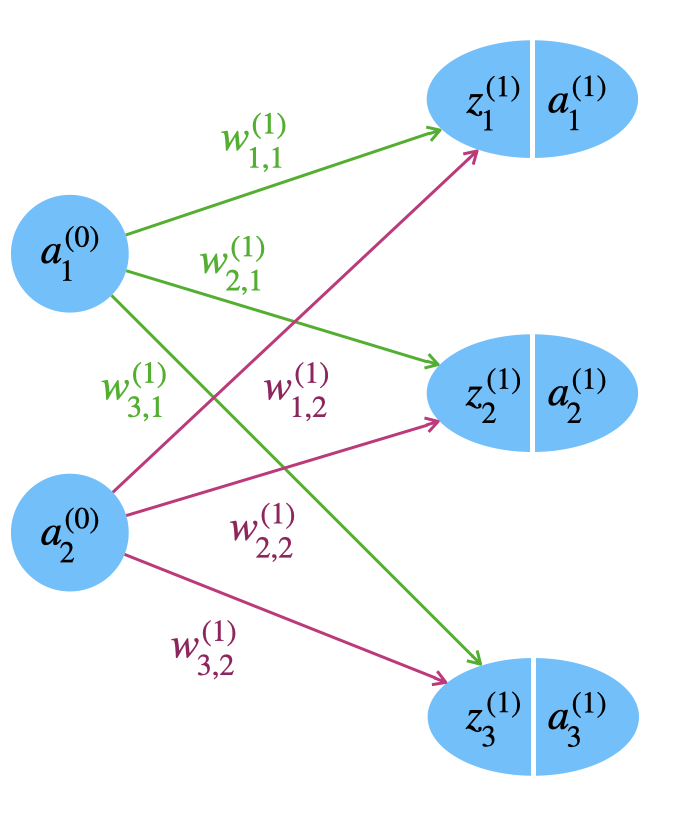
Wenden wir uns der Verarbeitung zu. Dazu betrachten wir \(a^{(0)}\) und \(z^{(1)}\) als Vektoren. Wir können den Rohinput der ersten Schicht \(z^{(1)}\) als Multiplikation der Gewichtsmatrix \(W^{(1)}\) mit dem Aktivierungsvektor \(a^{(0)}\) der Eingabe (Schicht 0) darstellen.
Im Beispiel wäre das die folgende Rechnung:
\[\left( \begin{array}{c} z_1^{(1)} \\ z_2^{(1)} \\ z_3^{(1)} \end{array} \right) = \begin{pmatrix} w_{1,1}^{(1)} & w_{1,2}^{(1)} \\ w_{2,1}^{(1)} & w_{2,2}^{(1)} \\ w_{3,1}^{(1)} & w_{3,2}^{(1)} \end{pmatrix} \left( \begin{array}{c} a_1^{(0)} \\ a_2^{(0)} \end{array} \right) = \left( \begin{array}{c} w_{1,1}^{(1)} \; a_1^{(0)} + w_{1,2}^{(1)} \; a_2^{(0)} \\ w_{2,1}^{(1)} \; a_1^{(0)} + w_{2,2}^{(1)} \; a_2^{(0)} \\ w_{3,1}^{(1)} \; a_1^{(0)} + w_{3,2}^{(1)} \; a_2^{(0)} \end{array} \right) \]
Wir können das in Vektorschreibweise sehr kompakt schreiben:
\[ z^{(1)} = W^{(1)} \; a^{(0)} \]
Allgemein gilt für eine beliebige Schicht \(l\):
\[ z^{(l)} = W^{(l)} \; a^{(l-1)} \]
wobei \(l \in {1,\ldots,L}\).
Multiplikationsreihenfolge W und a
Wie oben schon erwähnt, wird in einigen Fachbüchern auch die folgende Form gewählt \(z^{(l)} = (a^{(l-1)})^T \; W^{(l)}\). In dieser Formulierung drehen sich die Indizes von \(W\) um.
Bias-Neuronen
Jetzt fügen wir sogenannte Bias-Neuronen hinzu (engl. bias = Tendenz, Neigung, Verzerrung). Jede Schicht - außer der Ausgabeschicht - hat genau ein Bias-Neuron mit dem konstanten Aktivierungswert \(+1\), wie man in Abbildung 4.3 sieht. Die Einflussstärke des Bias-Neurons auf das Zielneuron \(i\) der nächsten Schicht \(l\) wird dann über das Gewicht \(b_i^{(l)}\) gesteuert.
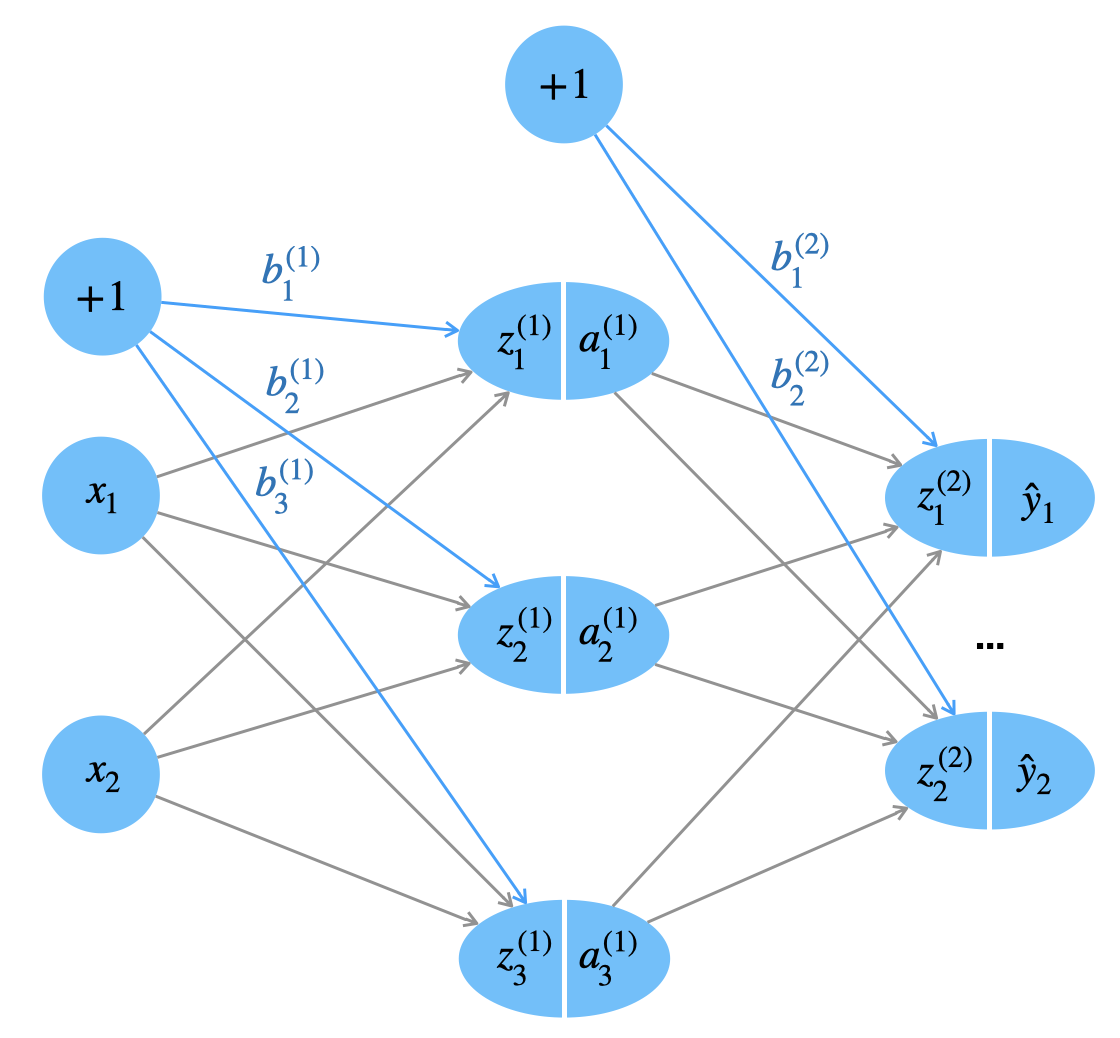
Innerhalb einer Schicht können wir die Gewichte des Bias-Neurons als Vektor schreiben. Man beachte, dass die Länge des Vektors der Anzahl der Zielneuronen entspricht:
\[b^{(l)} = \left( \begin{array}{c} b_1^{(l)} \\ \vdots \\ b_{n_{l}}^{(l)} \end{array} \right) \]
Im Gegensatz zum Perzeptron packen wir das Gewicht des Bias-Neurons nicht in die Gewichtsmatrix. Dies ist der üblichere Weg in der Literatur, vielleicht weil man dann in den Gleichungen nicht ständig das \(x\) mit einer “1” erweitern und die Bias-Gewichte in der Matrix gesondert betrachten muss. Beim Implementieren ist dann wieder die Lösung mit der Gewichtsmatrix potentiell interessant.
Die Roheingabe wird jetzt durch den Input des Bias-Neurons erweitert:
\[ \tag{Z} z_i^{(l)} = \sum_{j=1}^{n_{l-1}} w^{(l)}_{i,j} \; a_j^{(l-1)} + b_i^{(l)} \]
In Vektorform addieren wir einfach den Bias-Vektor zum Ergebnis der Matrizenmultiplikation. Das ist unsere erste Berechnungsformel für Forward Propagation:
\[ \tag{ZV} z^{(l)} = W^{(l)} \; a^{(l-1)} + b^{(l)} \]
Warum gibt es überhaupt diese Bias-Neuronen, die unsere schöne Formel oben noch ein bisschen komplexer machen? Kann man die nicht weglassen? Wenn Sie sich Abbildung 4.3 anschauen, sehen Sie, dass das Bias-Neuron im Gegensatz zu den anderen Neuronen derselben Schicht nicht von der Eingabe \(x\) abhängt. Das heißt, über das Bias-Gewicht kann ich den Wert eines Neurons “global” nach oben oder unten schieben, egal, wie der Input aussieht. Das entspricht tatsächlich in der klassischen Geradengleichung \(f(x) = ax + b\) dem \(b\) als y-Achsenabschnitt (wobei die Tatsache, dass das hier auch \(b\) heißt, Zufall ist). Auch dort schiebt das \(b\) den Wert nach oben oder nach unten, unabhängig von Eingabe \(x\).
Das Video erläutert die Vorwärtsverarbeitung des Feedforward-Netzes.
Anzahl der Parameter (Gewichte)
Wir überlegen uns kurz, wie viele Parameter unser Netz hat, denn die Komplexität des Netzwerks und damit sowohl Dauer als auch Speicherbedarf im Training hängen entscheidend davon ab. Parameter sind alle Größen, die im Training angepasst werden. Beim FNN sind das Gewichte in Gewichtsmatrizen und Bias-Vektoren.
Wir sehen uns nochmal das Netz in Abbildung 4.3 an: Zwischen Schicht 0 und 1 haben wir eine 3x2-Gewichtsmatrix und einen Bias-Vektor der Länge 3. Daraus ergeben sich 3x2 + 3 = 9 Parameter. Zwischen Schicht 1 und 2 haben wir eine 2x3 Gewichtsmatrix und einen Bias-Vektor der Länge 2, also 2x3 + 2 = 8 Parameter. Insgesamt hat das Beispielnetz also 17 Parameter. Zum Vergleich: heutige Konvolutionsnetze haben mehrere Millionen Parameter, GPT-3 hat 175 Milliarden Parameter.
Allgemein kann man die Anzahl der Parameter für eine Schicht \(l\) (\(l > 0\)) mit folgender Formel angeben:
\[ P_l = n_{l-1} n_l + n_l = n_l (n_{l-1} + 1) \]
Die Gesamtzahl der Parameter \(P\) ist also:
\[ P = \sum_{l=1}^L P_l = n_l (n_{l-1} + 1) \]
Das “+1” steht dort wegen der Bias-Gewichte.
Forward Propagation im Beispielnetz
In unserem Beispielnetz mit zwei Schichten läuft Forward Propagation wie folgt:
\[ x = a^{(0)} \, \overset{W^{(1)}}{\longrightarrow} \, z^{(1)} \, \overset{g}{\longrightarrow} \, a^{(1)} \, \overset{W^{(2)}}{\longrightarrow} \, z^{(2)} \, \overset{g}{\longrightarrow} \, a^{(2)} = \hat{y} \]
In Schicht \(0\) gilt:
\[ a^{(0)} = x \]
In Schicht \(1\) rechnen wir:
\[ \begin{align*} z^{(1)} & = W^{(1)} \; a^{(0)} + b^{(1)} \\[2mm] & = W^{(1)} \; x + b^{(1)} \\[2mm] a^{(1)} & = g(z^{(1)}) \end{align*} \]
Dann berechnen wir Schicht \(2\) und Ausgabe \(\hat{y}\):
\[ \begin{align*} z^{(2)} & = W^{(2)} \; a^{(1)} + b^{(2)} \\[2mm] a^{(2)} & = g(z^{(2)}) \\[2mm] \hat{y} & = a^{(2)} \end{align*} \]
4.1.3 Aktivierungsfunktion
Die Aktivierungsfunktion \(g\) ist von entscheidender Bedeutung für den Erfolg Neuronaler Netze, denn diese Funktion führt eine Nicht-Linearität in die Gesamtrechnung ein. Man mache sich klar, dass die Weiterleitung der Aktivierung über die Gewichte zur sogenannten Roheingabe eine lineare Abbildung ist:
\[ z_i^{(l)} = \sum_{j=1}^{n_{l-1}} \Big[ w^{(l)}_{i,j} \; a_j^{(l-1)} \Big] + b_i^{(l)} \]
Erst wenn die Aktivierungsfunktion \(g\) zum Zug kommt, wird eine (in der Regel) nicht-lineare Funktion eingeführt. Diese Berechnung ist die zweite wichtige Formel bei Forward Propagation:
\[ \tag{A} a_i^{(l)} = g(z_i^{(l)}) \]
Oben haben wir eine sigmoide Funktion für unser FNN gewählt. Man beachte, dass für die Ausgabe oft eine andere Aktivierungsfunktion gewählt wird als für die Zwischenschichten. Wir betrachten hier die Zwischenschichten.
Sigmoide Funktionen
Eine Sigmoidfunktion - wie die logistische Funktion - ist eine oft gewählte Aktivierungsfunktion für Zwischenschichten. Die Funktion ist so definiert:
\[ g(z) = \frac{1}{1 + e^{-z}} \]
Die logistische Funktion bildet den Input auf das Interval [0, 1] ab.
Alternativ kann man auch eine Funktion wählen, die auf das Interval [-1, 1] abbildet, das leistet z.B. der Tangens hyperbolicus (tanh).
Streng genommen nennt man beide Funktionen (logistisch und tanh) sigmoide Funktionen. Oft wird die logistische Funktion gleichgesetzt mit dem Begriff “Sigmoidfunktion” (z.B. auch in Keras). Der tanh kommt deutlich seltener zum Einsatz.
In der folgenden Abbildung sehen wir beide Funktionen im Vergleich:
def sigmoid(z):
return 1 / (1+np.exp(-z))
x = np.arange(-10, 10, .1)
y_sig = sigmoid(x)
y_tanh = np.tanh(x)
plt.plot(x, y_sig, 'b', label='logistisch')
plt.plot(x, y_tanh, 'r', label='tanh')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Logistische und tanh-Funktion')
plt.xticks([-10,-5,0,5,10])
plt.yticks([-1,-.5,0,.5, 1])
plt.grid()
plt.legend()
plt.show()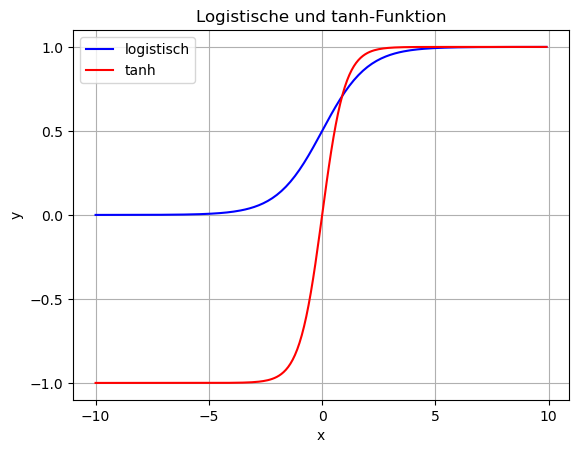
Rectified Linear Unit (ReLU)
Eine in den letzten Jahren wohl am meisten genutzte Funktion für Zwischenschichten ist das Rectified Linear Unit (ReLU). Diese ist definiert als
\[ g(z) := \max(0, z) \]
Für manche ist diese Darstellung vielleicht intuitiver:
\[ g(z) := \begin{cases} z &\mbox{wenn}\quad z > 0\\ 0 &\mbox{wenn}\quad z \leq 0 \end{cases} \]
Zu beachten ist, dass die Funktion nicht differenzierbar in 0 ist, dass dies aber in der Praxis kein Problem ist. Im Vergleich zur Heaviside-Funktion ist es aber so, dass die Steigung im positiven x-Raum natürlich beim Gradientenabstieg wichtig ist. Eine zweite Beobachtung ist, dass die Funktion zwar abschnittsweise linear ist, aber insgesamt wieder nicht-linear.
x = np.arange(-2, 2, .1)
y_relu = [max(0, i) for i in x]
plt.plot(x, y_relu, 'r', label='ReLU')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Rectified Linear Unit (ReLU)')
plt.xticks([-2,0,2])
plt.yticks([-.5,0,.5, 1])
plt.grid()
plt.legend()
plt.show()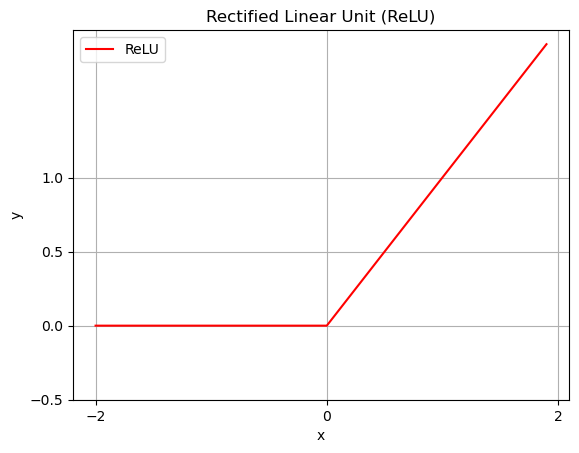
4.1.4 Softmax für die Ausgabe
Für die Ausgabe \(\hat{y}\) möchte man in einem Neuronalen Netz oft eine besondere Form haben. Jedes Ausgabeneuron repräsentiert ja eine bestimmte Klasse (z.B. Katze, Hund, Mensch bei einem Bildklassifikator). Daher wäre es wünschenswert, die entsprechenden Werte \(\hat{y}_1, \ldots, \hat{y}_m\) als Wahrscheinlichkeiten zu verstehen. Bedenken Sie, dass die Rohinputs ganz beliebige Werte annehmen können (z.B. deutlich größer als 1 oder negativ). Wenn die Werte in \(\hat{y}\) eine Wahrscheinlichkeitsverteilung bilden sollen, müssen sie zwei Eigenschaften aufweisen:
- alle Werte liegen zwischen 0 und 1
- die Summe aller Werte ergibt 1
Das ist tatsächlich gar nicht so schwer.
Einfaches Normalisieren
Wenn Sie eine Reihe von Werten \(z_1, \ldots, z_m\) haben (die zunächst mal alle positiv sind, also \(z_i \geq 0\)), dann “normalisieren” Sie einfach jeden Wert, indem Sie ihn durch die Summe aller Werte teilen:
\[ \tilde{z}_i = \frac{z_i}{\sum_{j=1}^m z_j} \]
Man sieht direkt, dass jeder Wert zwischen 0 und 1 liegen muss und dass die Summe aller \(z_i\) eins ist.
Softmax
Ähnlich funktioniert die Softmax-Funktion, die wir hier vorstellen. Bei Softmax wird der Wert \(z_i\) noch durch die Exponentfunktion “geschickt”, d.h. wir nehmen \(e^{z_i}\) statt \(z_i\). Schaut man sich die Funktion an (siehe Python-Ausgabe unten), sieht man zwei Eigenschaften:
- alle Eingangswerte \(z\) werden positiv
- negative Werte werden auf Werte kleiner 1 gemappt
- bei positiven Werten werden die Unterschiede stark “vergrößert”
x = np.arange(-3, 3, .1)
y = np.exp(x)
plt.plot(x, y, 'r')
plt.xlabel('z')
plt.ylabel('f')
plt.title('Funktion e^z im Bereich [-3, 3]')
plt.xticks(np.arange(-3,3,1))
plt.yticks(np.arange(0, 20, 5))
plt.grid()
plt.show()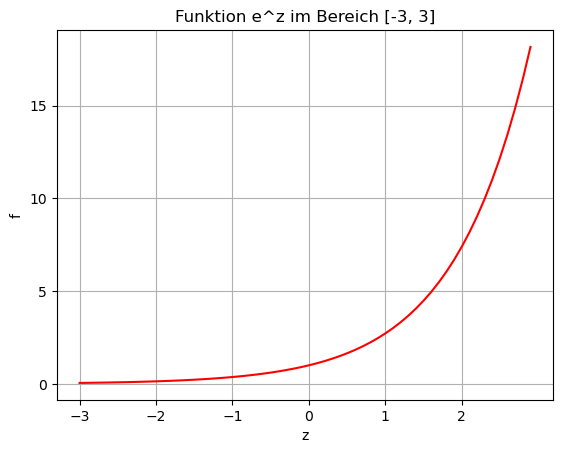
Die Softmax-Funktion ist jetzt wie folgt definiert (\(i \in \{1,\ldots,m\}\)):
\[ g_{sm}(z_i) := \frac{e^{z_i}}{\sum_{j=1}^m e^{z_j}} \]
Diese Funktion erfüllt beide Eigenschaften (wie Sie sich selbst leicht überzeugen können):
- alle \(\hat{y}_i\) liegen im im Interval [0, 1]
- die Summe aller Werte \(\hat{y}_1, \ldots, \hat{y}_m\) ist \(1\), d.h. \(\sum_i \hat{y}_i = 1\)
Sehen wir uns vier Beispielwerte an, die als Rohinput \(z_1, z_2, z_3, z_4\) bei vier Ausgabeneuronen ankommen könnten, zusammen mit der jeweiligen Softmax-Umrechnung (siehe auch den Code unten):
| z | softmax |
|---|---|
| -10.36 | 1.07 e-12 (= 0) |
| 0.71 | 6.87 e-08 (= 0) |
| 15.41 | 0.17 |
| 17.02 | 0.83 |
Sie sehen, dass die Werte im Interval [0,1] liegen und die Unterschiede akzentuiert werden.
Softmax im Vergleich zu anderen Aktivierungsfunktionen
Im Unterschied zu den bisherigen Aktivierungsfunktionen (z.B. logistische Funktion oder ReLU) wird bei Softmax die gesamte Werteverteilung in die Rechnung mit einbezogen (durch die Summe im Nenner), d.h. die Werte sind immer relativ zu allen anderen Werten.
Softmax in Python und Beispiele
Wir sehen uns die Funktion in Python an und geben gleich ein paar Beispiele für Rohinput-Verteilungen aus.
# Als Eingabe wird ein NumPy-Array erwartet
def softmax(n):
expnum = np.exp(n) # exp auf alle Arraywerte (np.exp für Broadcasting)
s = expnum.sum() # Summe aller Werte
return expnum/s # Broadcasting der Division
# Funktion für die Ausgabe
def print_softmax(num):
sm = softmax(num)
for i in range(len(num)):
print(f"Rohinput: {num[i]:7.2f} => Softmax: {sm[i]:.5f}")
# Beispiele:
n1 = np.array([0, 1, 0, 0])
print_softmax(n1)
n2 = np.array([-10, 100, -10, -90])
print('\n')
print_softmax(n2)
n3 = np.array([-3, -2, -1, 0, 1, 2, 3])
print('\n')
print_softmax(n3)
n4 = np.array([-10.36, 0.71, 15.41, 17.02])
print('\n')
print_softmax(n4)Rohinput: 0.00 => Softmax: 0.17488
Rohinput: 1.00 => Softmax: 0.47537
Rohinput: 0.00 => Softmax: 0.17488
Rohinput: 0.00 => Softmax: 0.17488
Rohinput: -10.00 => Softmax: 0.00000
Rohinput: 100.00 => Softmax: 1.00000
Rohinput: -10.00 => Softmax: 0.00000
Rohinput: -90.00 => Softmax: 0.00000
Rohinput: -3.00 => Softmax: 0.00157
Rohinput: -2.00 => Softmax: 0.00426
Rohinput: -1.00 => Softmax: 0.01159
Rohinput: 0.00 => Softmax: 0.03150
Rohinput: 1.00 => Softmax: 0.08563
Rohinput: 2.00 => Softmax: 0.23276
Rohinput: 3.00 => Softmax: 0.63270
Rohinput: -10.36 => Softmax: 0.00000
Rohinput: 0.71 => Softmax: 0.00000
Rohinput: 15.41 => Softmax: 0.16659
Rohinput: 17.02 => Softmax: 0.833414.1.5 Formeln für Forward Propagation im Überblick
Wir schauen uns nochmal alle Formeln, die wir für die Vorwärtsverarbeitung (Forward Propagation) benötigen, im Überblick an. Dabei bezeichnet \(L\) die Anzahl der Schichten, \(n_l\) die Zahl der Neuronen in Schicht \(l\) und \(m\) die Anzahl der Ausgabeneuronen.
Komponentenschreibweise
Zunächst schreiben wir die Formeln so, dass nur Skalare erscheinen (also keine Vektoren oder Matrizen). Index \(i\) bezieht sich auf ein Neuron der Schicht \(l\).
\[ \begin{align} a^{(0)}_i &:= x_i \tag{Eingabeschicht}\\[3mm] z^{(l)}_i &:= \sum_{j=1}^{n_{l-1}}\Big[ w_{i, j}^{(l)} \; a_j^{(l-1)}\Big] + b_i^{(l)} \tag{Roheingabe}\\[3mm] a^{(l)}_i &:= g(z^{(l)}_i) \tag{Aktivierung}\\[3mm] \hat{y}_i &:= a^{(L)}_i\tag{Ausgabe} \end{align} \]
Vektorschreibweise
Jetzt sehen wir uns die Schreibweise mit Vektoren und Matrizen an.
\[ \begin{align} a^{(0)} &:= x \tag{Eingabeschicht}\\[3mm] z^{(l)} &:= W^{(l)}\, a^{(l-1)} + b^{(l)}\tag{Roheingabe}\\[3mm] a^{(l)} &:= g(z^{(l)}) \tag{Aktivierung}\\[3mm] \hat{y} &:= a^{(L)}\tag{Ausgabe} \end{align} \]
Aktivierungsfunktionen
Für die Aktivierungsfunktion \(g\) wählen wir zwei unterschiedliche Funktionen. Wir definieren beide in Komponentenschreibweise.
Wir wählen die Sigmoidfunktion für die Zwischenschichten \(l = 1, \ldots, L-1\):
\[ g(z_i) := \frac{1}{1 + e^{-z_i}} \]
Wir wählen die Softmax-Funktion für die Ausgabeschicht \(L\):
\[ g_{sm}(z_i) := \frac{e^{z_i}}{\sum_{j=1}^m e^{z_j}} \]
4.2 Lernen mit Backpropagation
Backpropagation ist eine Methode, um die Gewichte schrittweise so anzupassen, dass sie sich einer optimalen Lösung annähern. Bei Backpropagation wird wieder das Verfahren des Gradientenabstiegs eingesetzt, um die optimalen Gewichte zu finden. Wie bei jedem Optimierungsproblem müssen wir auch hier eine Zielfunktion definieren, auch Kosten-, Fehler- oder Verlustfunktion genannt. Diese Zielfunktion gilt es zu minimieren. Beim Gradientenabstieg wird dazu die Ableitung der Zielfunktion (= Gradient) verwendet.
Die Verfahren hinter Backpropagation wurden bereits in den 60er Jahren im Bereich Kontrolltheorie/Regelungstheorie entwickelt, aber erst in den 1974 für die Anwendung in Neuronalen Netzen durch Paul Werbos (1974; 1982) “wiederentdeckt”. Wirkliche Verbreitung findet die Methode in den 80ern dann durch Rumelhart, Hinton, and Williams (1986), die auch den Begriff Backpropagation prägten. Siehe auch Schmidhuber (2015) für einen Überblick zur Geschichte des Verfahrens.
Wenn Sie etwas zur Entstehungsgeschichte von Backprop um die Person David Rumelhart in den 80er Jahren hören möchten, horchen Sie in den Lex-Fridman-Podcast mit den Gast Jay McClelland hinein (etwa ab 01:12:35; oder Sie schauen sich einen kurzen Clip an, wo McClelland über Geoffrey Hinton und seine Rolle bei Backpropagation spricht). McClelland gehört ebenfalls zu den Pionieren der Arbeit an Neuronalen Netzen, die damals unter den Begriff Konnektionismus und in die größere Disziplin der Kognitionswissenschaften fielen. Rumelhart ist leider 2011 im Alter von 68 Jahren verstorben.
Geoffrey E. Hinton ist wissenschaftlich auch heute noch sehr aktiv und gilt als einer der Pioniere des Deep Learning. Er erhielt 2018 den renommierten Turing Award der ACM, zusammen mit Yann LeCun und Yoshua Bengio. Wenn Sie diesen “grandfather of deep learning” sprechen hören wollen, gibt es viele Vorträge im Internet, z.B. Will digital intelligence replace biological intelligence? vom 02.02.2024.
Lesenswert
- Jürgen Schmidhuber: Who Invented Backpropagation?
- Wikipedia (en) zu Gradient Descent
- Wikipedia (de) zu Optimierung
4.2.1 Zielfunktion
Da wir es wieder mit einem Optimierungsproblem zu tun haben, benötigen wir eine Zielfunktion (engl. objective function), die wir minimieren oder maximieren.
Wir entscheiden uns für das Minimieren und suchen also eine Kostenfunktion oder Verlustfunktion, engl. loss function. Abbildung 4.4 zeigt die prinzipielle Idee der “Fehlermessung”: Es wird immer der berechnete Output mit dem gewünschten Output verglichen (in der Abbildung für ein einziges Trainingsbeispiel). Wir betrachten zunächst den Fall der binären Klassifikation und gehen dann zur Mehrklassen-Klassifikation mit \(m\) Klassen über.
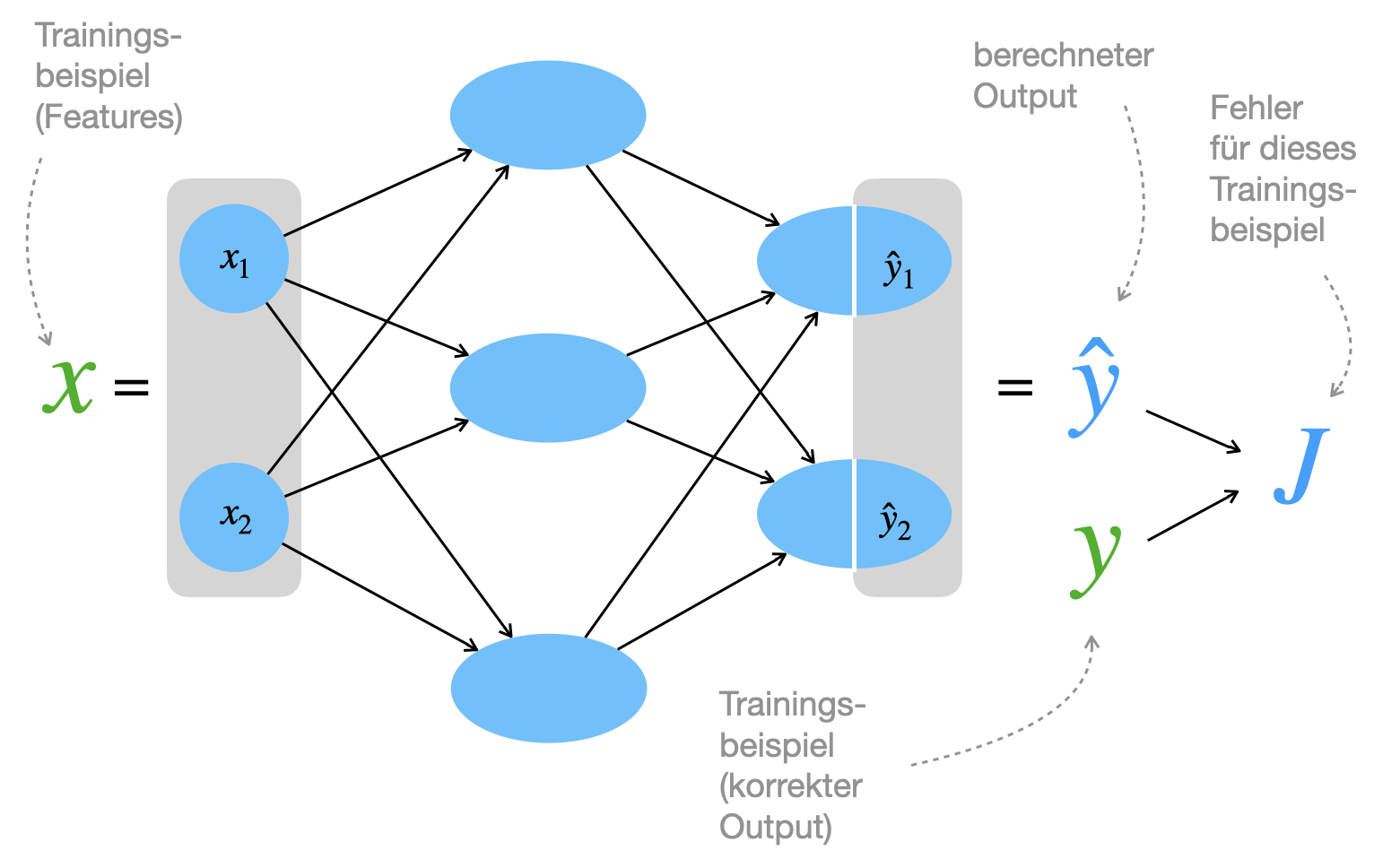
Binary Cross-Entropy für binäre Klassifikaion
Zunächst definieren wir die Kostenfunktion \(J\) für binäre Klassifikation, d.h. es gibt nur ein einziges Ausgabeneuron mit Ausgabewert \(\hat{y}\) (zum Beispiel 1 = SPAM, 0 = kein SPAM). Wir betrachten ferner nur ein einziges Trainingsbeispiel \((x^k, y^k)\). Wir definieren jetzt die sogenannte Binary Cross-Entropy Funktion als Verlustfunktion wie folgt
\[ J_k := - \Big( y \; log(\hat{y}) + (1 - y) \; log(1 - \hat{y}) \Big) \]
Wir haben den Index \(k\) bei \(y\) und \(\hat{y}\) der Lesbarkeit halber weggelassen.
Diese Formel ist nicht so kryptisch ist, wie sie zunächst scheint. Der Zielwert \(y\) ist immer entweder genau 0 oder genau 1, also \(y \in \{0,1\}\), d.h. es wird immer einer der beiden Summanden “ausgewählt” und der andere “gelöscht”.
Man kann also auch schreiben:
\[ J_k = \begin{cases} - log(\hat{y}) & \quad \text{falls } y = 1 \\[3mm] - log(1 - \hat{y}) & \quad \text{falls } y = 0 \end{cases} \]
Aufgrund von Softmax liegt der berechnete Output \(\hat{y}\) irgendwo zwischen 0 und 1. Wenn der Zielwert \(y=1\) ist, dann ist der Fehler \(J_k\) die negative Log-Funktion (siehe Abbildung unten). Die negative Log-Funktion wird nahe 0 sehr groß (hoher Fehler) und nahe 1, also nahe dem gewünschten Zielwert, sehr klein und gleich 0, wenn wir die 1 erreichen. Das ist also sinnvoll.
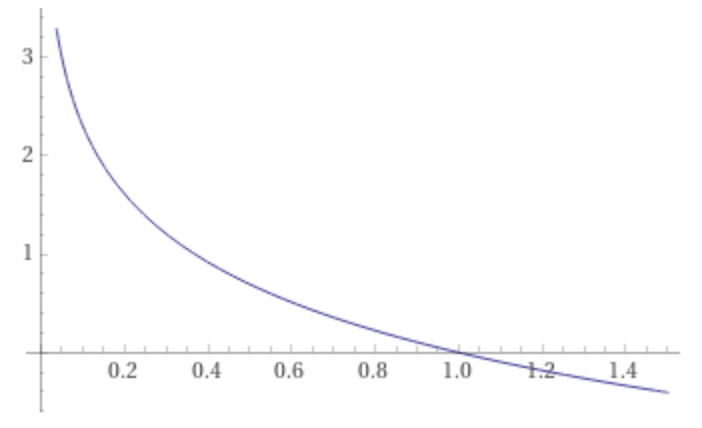
Wir sehen uns jetzt für den Fall, dass der Zielwert \(y = 1\) ist, eine Wertetabelle an:
| Zielwert \(y\) | Vorhersage \(\hat{y}\) | log(\(\hat{y}\)) | - log(\(\hat{y}\)) |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 1 | 0.9 | -0.11 | 0.11 |
| 1 | 0.5 | -0.69 | 0.69 |
| 1 | 0.1 | -2.30 | 2.30 |
| 1 | 0.00001 | -11.51 | 11.51 |
Auch hier sehen wir: Wenn die Vorhersage \(\hat{y}\) richtig liegt, dann ist der Fehler genau 0. Je weiter der vorhergesagte Wert vom Zielwert abweicht, umso größer der Fehlerbeitrag. Der Fehler steigt sogar exponentiell nahe 0. Man bedenke, dass \(log(0)\) nicht definiert ist (minus unendlich), deshalb haben wir in der Tabelle auch nur einen sehr kleinen Wert genommen. Die Null müsste man auch in einer Implementierung entsprechend abfangen.
Für den Fall \(y = 0\) gilt natürlich das gleiche wie oben, die Werte werden durch \(1-\hat{y}\) entsprechend “umgedreht”.
In Keras konfiguriert man die loss function, wenn man die Methode compile auf dem Modell aufruft:
model.compile(optimizer='sgd',
loss='binary_crossentropy',
metrics=['acc'])Wir sehen uns im nächsten Abschnitt den Fall an, dass mehrere Klassen vorliegen.
Categorical Cross-Entropy
In den meisten Fällen haben wir es mit Mehrklassen-Klassifikation zu tun. Im Gegensatz zur binären Klassifikation haben wir hier mehrere Output-Neuronen vorliegen (pro Klasse ein Neuron, also eine One-Hot-Encoding). Als Aktivierung in der Ausgabeschicht wird dann die Softmax-Funktion verwendet, so dass der berechnete Output immer als Wahrscheinlichkeitsverteilung über alle Klassen vorliegt.
In diesem Fall verwendet man als Verlustfunktion die sogenannte Categorical Cross-Entropy. Bei einer Mehrklassen-Klassifikation mit \(m\) Klassen und One-Hot-Encoding ist die Fehlerfunktion für ein Trainingsbeispiel \(k\) wie folgt definiert:
\[ \tag{J} J_k = - \sum_{i=1}^m y_i^k\, log(\hat{y}_i^k) \]
Die Idee ist hier, dass alle Komponenten, die nicht der Zielklasse entsprechen, ignoriert werden. Zum Beispiel: Die Daten enthalten 5 Kategorien (\(m=5\)) und bei einem Trainingsbeispiel \(k=3\) ist die korrekte Ausgabe wäre die 2. Kategorie, also
\[ y^3 = \begin{pmatrix} 0\\1\\0\\0\\0 \end{pmatrix} \]
Dann ist der Fehlerbeitrag für dieses Trainingsbeispiel 3:
\[J_3 = - log(\hat{y}_2^3) \]
Das heißt, man schaut sich in diesem Fall nur den Output von Ausgabeneuron Nr. 2 an und nimmt dort noch den Logarithmus. Die Begründung für den negativen Logarithmus haben wir oben bei Binary Cross-Entropy besprochen.
Anmerkung
Man könnte sich fragen, ob es ein Problem ist, dass alle Aktivierungen der nicht-korrekten Klasse ignoriert werden. Würde ein Modell dann nicht einfach lernen, bei allen Klassen eine 1 zu produzieren? Hier ist die Softmax-Funktion wesentlich, die dafür sorgt, dass die nicht-korrekten Klassen indirekt addressiert werden, da sich alle Aktivierungen zu 1 aufsummieren.
Wir haben oben nur den Fehler \(J_k\) bei einem einzigen Trainingsbeispiel \(k\) definiert. Nehmen wir an, wir haben \(N\) Trainingsbeispiele \((x^k, y^k)\). Jetzt addieren wir die Kosten aller Trainingsbeispiele auf und mitteln sie:
\[ \tag{J2} J = - \frac{1}{N} \sum_{k=1}^N \sum_{i=1}^m y_i^k\, log(\hat{y}_i^k) \]
Das entspricht der Summe der Fehlerfunktionen für einzelne Trainingsbeispiele:
\[ J = \frac{1}{N} \sum_{k=1}^N J_k \]
Da \(J\) von den aktuellen Gewichten \(W\) abhängt, schreibt man auch \(J(W)\) oder \(J_W\). Wir lassen diesen Hinweis aber i.d.R. weg.
In Keras gibt man categorical_crossentropy für die loss function in der Methode compile des Modells an:
model.compile(optimizer='sgd',
loss='categorical_crossentropy',
metrics=['acc'])4.2.2 Regularisierung
Man fügt den folgenden Term zur Kostenfunktion dazu, um zu verhindern, dass die individuelle Gewichte zu dominant werden. Man kann zeigen, dass dies den Effekt des Overfitting verringert. Man kann sich das so vorstellen, dass ein zu schnelles Abdriften in eine extreme Gewichtsverteilung (ein paar Gewichte werden sehr groß) dadurch verhindert wird, dass dieser “Strafterm” zu den Kosten hinzuaddiert wird. Effektiv wird dadurch die absolute Größe der Gewichte verringert, daher spricht man auch von weight decay (siehe auch unten unter “Effekt”).
Wir addieren die Beträge aller Gewichtsmatrizen von allen Schichten:
\[ \frac{\lambda}{2} \: \sum_{l=1}^{L} \left\Vert W^{(l)} \right\Vert^2 \]
wobei die L2-Norm einer Matrix \(W\) definiert ist als Wurzel der quadrierten Komponenten:
\[ \tag{N} \left\Vert W \right\Vert = \left( \sum_i \sum_j (w_{i,j})^2 \right)^{\frac{1}{2}}\]
Dies nennt man auch L2-Regularisierung, da hier die L2-Norm angewandt wird. Die L1-Regularisierung würde die Beträge der Gewichte verwenden (= L1-Norm). Der Faktor \(\lambda\) (griechischer Buchstabe Lambda) steuert die Stärke der Regularisierung.
Finale Zielfunktion (mit Categorical Cross-Entropy)
Wir addieren den L2-Regularisierungsterm zu unserer Kostenfunktion (J) und lösen dann den Regularisierungsterm mit Hilfe von (N) auf.
\[ \begin{align*} J_\text{reg} &= J + \frac{\lambda}{2} \sum_{l=1}^{L} \left\Vert W^{(l)} \right\Vert^2 \\ &= J + \frac{\lambda}{2} \: \sum_{l=1}^{L} \sum_{j=1}^{n_{l-1}} \sum_{h=1}^{n_l} (w^{(l)}_{h, j})^2 \\ &= - \frac{1}{N} \sum_{k=1}^N \sum_{i=1}^m y_i^k\, log(\hat{y}_i^k) \, + \frac{\lambda}{2} \: \sum_{l=1}^{L} \sum_{j=1}^{n_{l-1}} \sum_{h=1}^{n_l} (w^{(l)}_{h, j})^2 \end{align*} \]
Dies wäre also unsere vollständige Zielfunktion.
Effekt der Regularisierung (Weight Decay)
Wir möchten überlegen, wie genau die Regularisierung wirkt. Dazu unterscheiden wir die Kostenfunktion ohne Regularisierung \(J\) und die Kostenfunktion mit Regularisierung \(J_\text{reg}\). Der Zusammenhang ist:
\[\tag{R} J_\text{reg} = J + \frac{\lambda}{2} \sum_{l=1}^{L} \left\Vert W^{(l)} \right\Vert^2 \]
Jetzt schauen wir uns den Update-Schritt der Gewichte an:
\[ w_{i,j} := w_{i,j} + \alpha \Delta w_{i,j} \tag{*}\label{update}\]
Das Delta berechnet sich wie folgt:
\[ \Delta w_{i,j} = - \frac{\partial}{\partial w_{i,j}} J_\text{reg} \]
Wir setzen (R) ein:
\[ \begin{align*} \Delta w_{i,j} &= - \frac{\partial}{\partial w_{i,j}} \left[ J + \frac{\lambda}{2} \: \sum_{l=1}^{L} \left\Vert W^{(l)} \right\Vert^2 \right] \\ &= - \left[ \frac{\partial}{\partial w_{i,j}} \frac{\lambda}{2} \: \sum_{l=1}^{L} \left\Vert W^{(l)} \right\Vert^2 + \frac{\partial}{\partial w_{i,j}} J \right] \end{align*} \tag{**}\label{delta} \]
Jetzt gilt Folgendes aufgrund von (N):
\[ \frac{\partial}{\partial w_{i,j}} \frac{\lambda}{2} \: \sum_{l=1}^{L} \left\Vert W^{(l)} \right\Vert^2 = \lambda\,w_{i,j} \]
(Das \(w_{i,j}\) gehört zu einer bestimmten Schicht \(h\), was wir hier nicht explizit hingeschrieben haben. Daher fallen alle Terme anderer Schichten weg.)
Wir setzen dies in (\(\ref{delta}\)) ein:
\[ \Delta w_{i,j} = - \left[ \lambda\,w_{i,j} + \frac{\partial}{\partial w_{i,j}} J \right] \]
Das setzen wir wieder in (\(\ref{update}\)) ein und formen um:
\[ \begin{align*} w_{i,j} &:= w_{i,j} - \alpha \left[ \lambda\,w_{i,j} + \frac{\partial}{\partial w_{i,j}} J \right]\\ &= \left(1 - \alpha \lambda \right) w_{i,j} - \alpha \frac{\partial}{\partial w_{i,j}} J \end{align*} \]
Wir haben jetzt wieder ungefähr die Formel in (\(\ref{update}\)). Im Unterschied zur ursprünglichen Formel sieht man aber, dass das Gewicht \(w_{i,j}\) in jedem Schritt ein wenig reduziert wird, denn \((1- \alpha \lambda)\) ist ja ein Faktor, der echt kleiner als eins ist. Deshalb wird auch von weight decay gesprochen.
4.2.3 Fehlerberechnung (Delta)
Wir kommen jetzt zu den ersten Berechnungen, um letztlich die Gewichte anzupassen. Allgemein verläuft bei Backpropagation - im Gegensatz zur Forward Propagation - der Fluß der Verarbeitung von der letzten Schicht rückwärts. An den Neuronen berechnen wir auf diese Weise zunächst “Fehlerwerte”. Diese Fehler verwenden wir später, um die Gewichte anzupassen, wie wir das schon beim Perzeptron getan haben.
Den Fehler in der Output-Schicht zu definieren, ist relativ offensichtlich, aber weniger klar bei den versteckten Neuronen. Alle Fehler werden hier mit \(\delta\) (griechisches kleines Delta) bezeichnet, da “Delta” in der Mathematik immer auf eine Differenz hindeutet.
In der folgenden Abbildung sehen wir in unserem Beispielnetz, wo die Fehler \(\delta^{(1)}\) und \(\delta^{(2)}\) berechnet werden. In der Eingabeschicht gibt es keinen Fehler, weil dort ja das Trainingsbeispiel anliegt. Die Biasneuronen ignorieren wir hier.
Berechnung
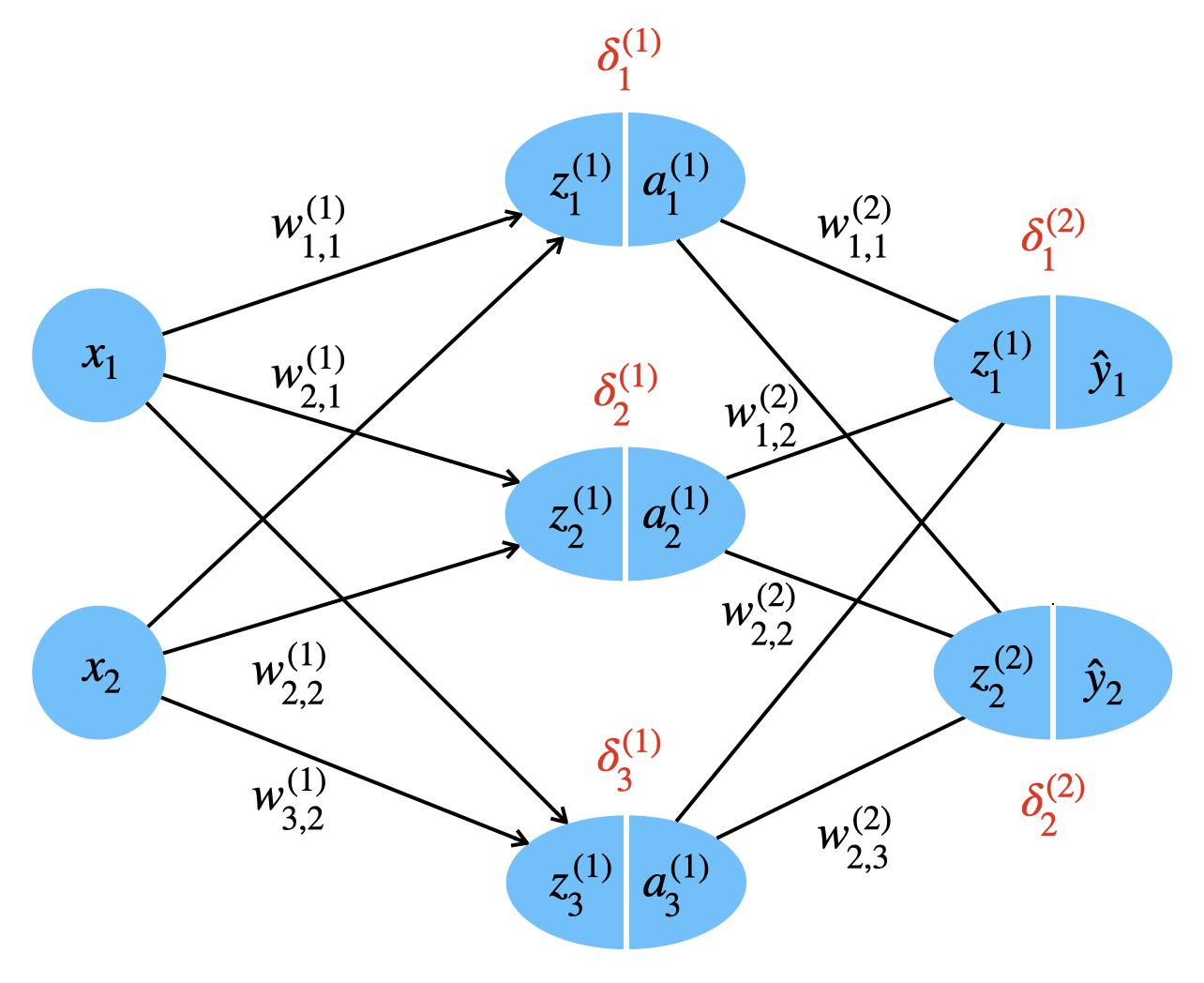
Grob gesehen haben wir die folgende Verarbeitungskette in unserem Beispiel-Netz:
- berechne \(\delta^{(2)}\) unter Verwendung der errechneten Ausgabe \(\hat{y}\)
- berechne \(\delta^{(1)}\) unter Verwendung des errechneten \(\delta^{(2)}\)
Wie man sieht, läuft die Berechnung rückwärts durch die Schichten, von Schicht 2 zu Schicht 1.
Fehler in der Ausgabeschicht
Allgemein definieren wir zunächst den Fehler \(\delta\) für die Ausgabeschicht \(L\). Hier zunächst mal für jedes Neuron \(i\):
\[ \delta_i^{(L)} = \hat{y}_i - y_i \]
In der Vektordarstellung können wir den Index weglassen:
\[ \delta^{(L)} = \hat{y} - y \]
Die Herleitung finden Sie im nächsten Kapitel 7 unter (D1).
Fehler in beliebiger Schicht
Für eine beliebige Schicht \(l\), außer Aus- oder Eingabeschicht, d.h. \(l \in \{1, \ldots, L-1\}\), berechnet sich \(\delta^{(l)}\) wie folgt:
\[ \delta^{(l)} = (W^{(l+1)})^T \; \delta^{(l+1)} \odot g'(z^{(l)}) \]
wobei der Operator \(\odot\) die elementweise Multiplikation von Vektoren ausdrückt, auch bekannt als Hadamard product. Ein Beispiel:
\[\left( \begin{array}{c} a_1 \\ a_2 \\ a_3 \end{array} \right) \odot \left( \begin{array}{c} b_1 \\ b_2 \\ b_3 \end{array} \right) = \left( \begin{array}{c} a_1 b_1\\ a_2 b_2\\ a_3 b_3\end{array} \right) \]
Die Herleitung der obigen Formel für \(\delta^{(l)}\) finden Sie im nächsten Kapitel 7 unter (D2).
Etwas kompakter schreiben wir:
\[ \label{backprop1}\tag{D} \delta^{(l)} = \begin{cases} \hat{y} - y & \mbox{wenn}\quad l = L\\[3mm] (W^{(l+1)})^T \; \delta^{(l+1)} \odot g'(z^{(l)}) & \mbox{wenn}\quad l \in \{1, \ldots, L-1\} \end{cases} \]
Wenn wir uns das schematisch ansehen, sehen wir, dass jedes Neuron seinen eigenen “Fehlerwert” \(\delta\) hat. Ausgenommen sind die Eingabeneuronen, was sinnvoll ist, denn die Eingabedaten sind ja die Features eines Trainingsbeispiels und können daher nicht “falsch” sein.
In einem Übungsblatt haben wir gezeigt, dass die Ableitung \(g'\) für die logistische Funktion wie folgt aussieht:
\[g'(z^{(l)}) = a^{(l)} \odot (1 - a^{(l)})\]
so dass wir schreiben können:
\[ \tag{D'}\delta^{(l)} = \begin{cases} \hat{y} - y & \mbox{wenn}\quad l = L\\[3mm] (W^{(l+1)})^T \; \delta^{(l+1)} \odot a^{(l)} \odot (1 - a^{(l)})& \mbox{wenn}\quad l \in \{1, \ldots, L-1\} \end{cases} \]
Man sieht, dass man zur Berechnung von \(\delta^{(l)}\) lediglich den Fehler der direkt nachgelagerten Schicht \(l+1\), die Aktivierung der eigenen Schicht \(l\) und der Gewichte zwischen den Schichten \(l\) und \(l+1\) benötigt. Mit dieser Formel ist somit es möglich, ein \(\delta\) für jedes Neuron zu berechnen, indem man schichtweise rückwärts von Outputschicht zu Inputschicht vorgeht. Daher der Name Backpropagation (Rückwärtsverarbeitung).
Hinweis
Formel (D) ist allgemeiner, da verschiedene Aktivierungsfunktionen \(g\) zum Einsatz kommen können. Für die Herleitung betrachten wir aber das speziellere (D’).
Intuition
Wenn wir uns eine einzelne Komponente \(i\) eines \(\delta\) ansehen, erkennen wir, welche Werte in die Rechnung eingehen:
\[ \delta_i^{(l)} = a_i^{(l)} \: (1 - a_i^{(l)}) \: \sum_j w_{j,i}^{(l+1)} \: \delta_j^{(l+1)}\]
Schauen wir uns ein konkretes \(\delta_2^{(1)}\) an (siehe Abb. unten). Dies soll den Einfluss des Neurons 2 in Schicht 1 auf die Fehler in der Ausgabeschicht 2 erfassen.
\[ \delta_2^{(1)} = a_2^{(1)} \: (1 - a_2^{(1)}) \: \sum_{j=1}^2 w_{j,2}^{(2)} \: \delta_j^{(2)}\]
Schematisch sehen wir, welche Daten für die Berechnung von \(\delta_2^{(1)}\) benötigt werden, nämlich insbesondere alle Fehlerwerte der nachfolgenden Schicht, aber auch die Gewichte dorthin und die Aktivierung des Neurons.
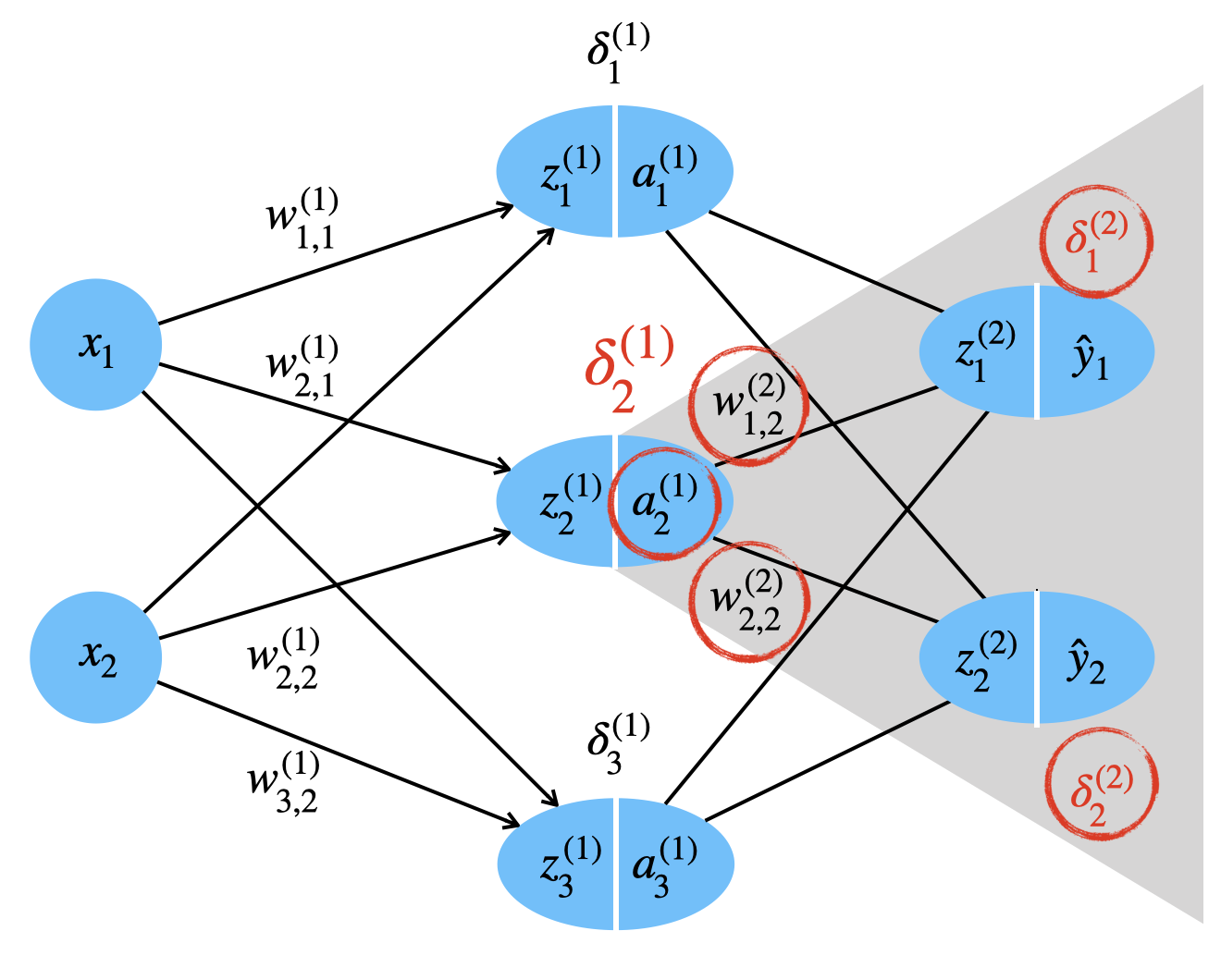
Zunächst scheint die Summe plausibel: man gewichtet die zwei Komponenten im Fehler \(\delta^{(2)}\) je nachdem, wie hoch das Gewicht - also der Einfluss des Neurons - auf die jeweilige Fehlerkomponente war.
Der Term \(a\: (1 - a)\) entspricht der Ableitung der Aktivierungsfunktion, also \(g'(z)\). Dies ist also die “Richtung” der Änderung und ist als Teil des Gradienten dieser Schicht für den Gradientenabstieg wesentlich.
4.2.4 Gewichtsanpassung
Jetzt wollen wir unsere Fehlerwerte nutzen, um die Gewichte anzupassen.
Anpassung des Gewichts \(w_{i,j}^{(l)}\) bedeutet, ein Delta zu addieren. Wie gewohnt steuern wir den Grad der Änderung mit einem Faktor \(\alpha \in [0, 1]\), der Lernrate.
\[ w_{i,j}^{(l)} := w_{i,j}^{(l)} + \alpha \; \Delta w_{i,j}^{(l)} \]
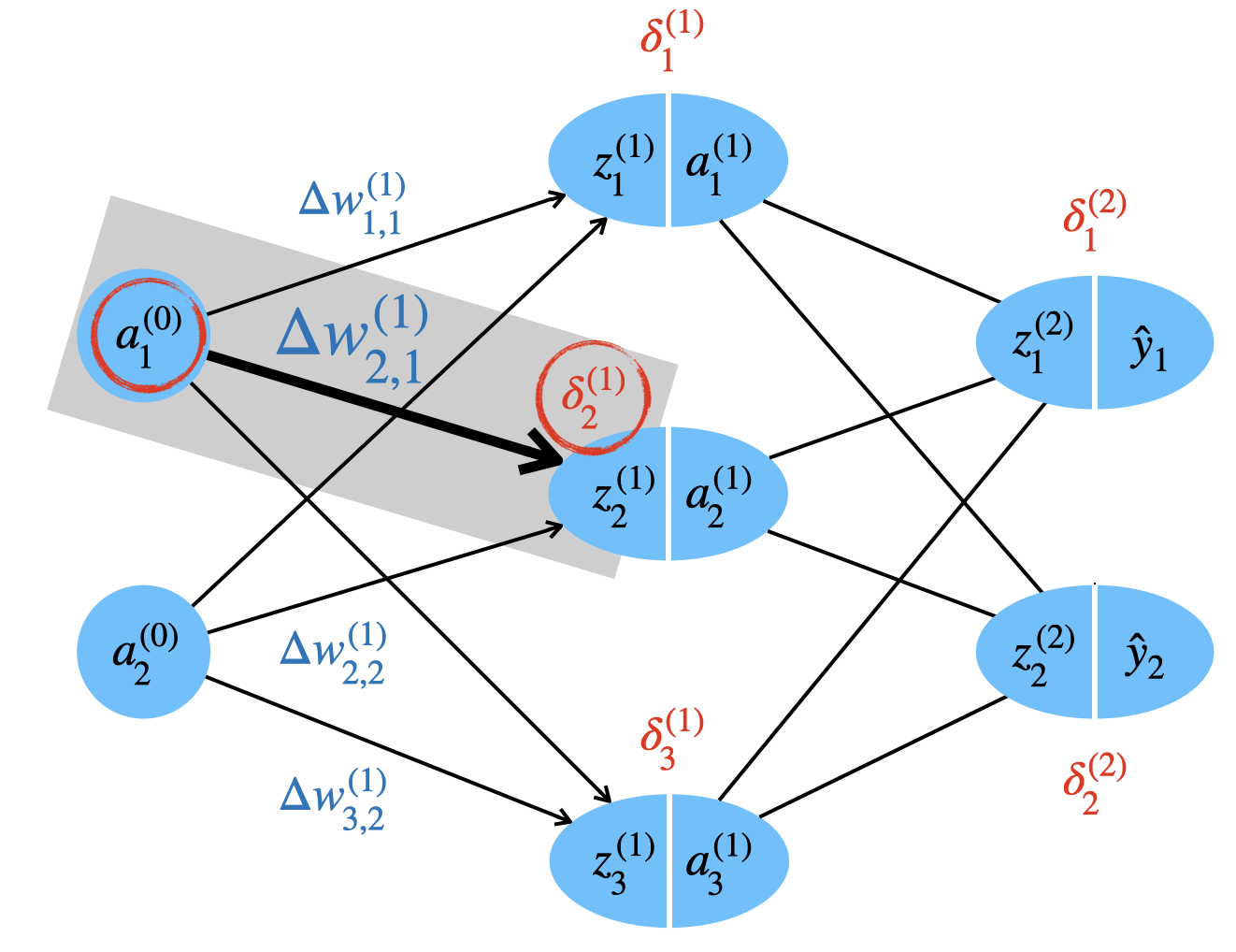
Wir müssen \(\Delta w_{i,j}^{(l)}\) für jedes Gewicht berechnen, wie die folgende Abbildung illustriert.
Wir benutzen auch hier wieder Gradientenabstieg, d.h. wir fragen uns, in welche Richtung und wie stark wir \(w_{i,j}\) ändern müssen, indem wir die partielle Ableitung der Zielfunktion hinsichtlich \(w_{i,j}\) bilden.
Wir werden später noch zeigen, dass gilt:
\[ \frac{\partial J}{\partial w_{i,j}^{(l)}} = a_j^{(l-1)} \: \delta_i^{(l)} \]
Wir müssten hier noch einen Term für die L2-Regularisierung addieren, lassen ihn aber um der Lesbarkeit willen weg. Die Formel oben gilt also für den Fall \(\lambda = 0\).
Diese Ableitung ist genau das, was wir für unser Delta benötigen, denn das Delta soll ja in Richtung negative Richtung des Gradienten zeigen.
\[ \Delta w_{i,j}^{(l)} = - \frac{\partial J}{\partial w_{i,j}^{(l)}} = - a_j^{(l-1)} \: \delta_i^{(l)} \]
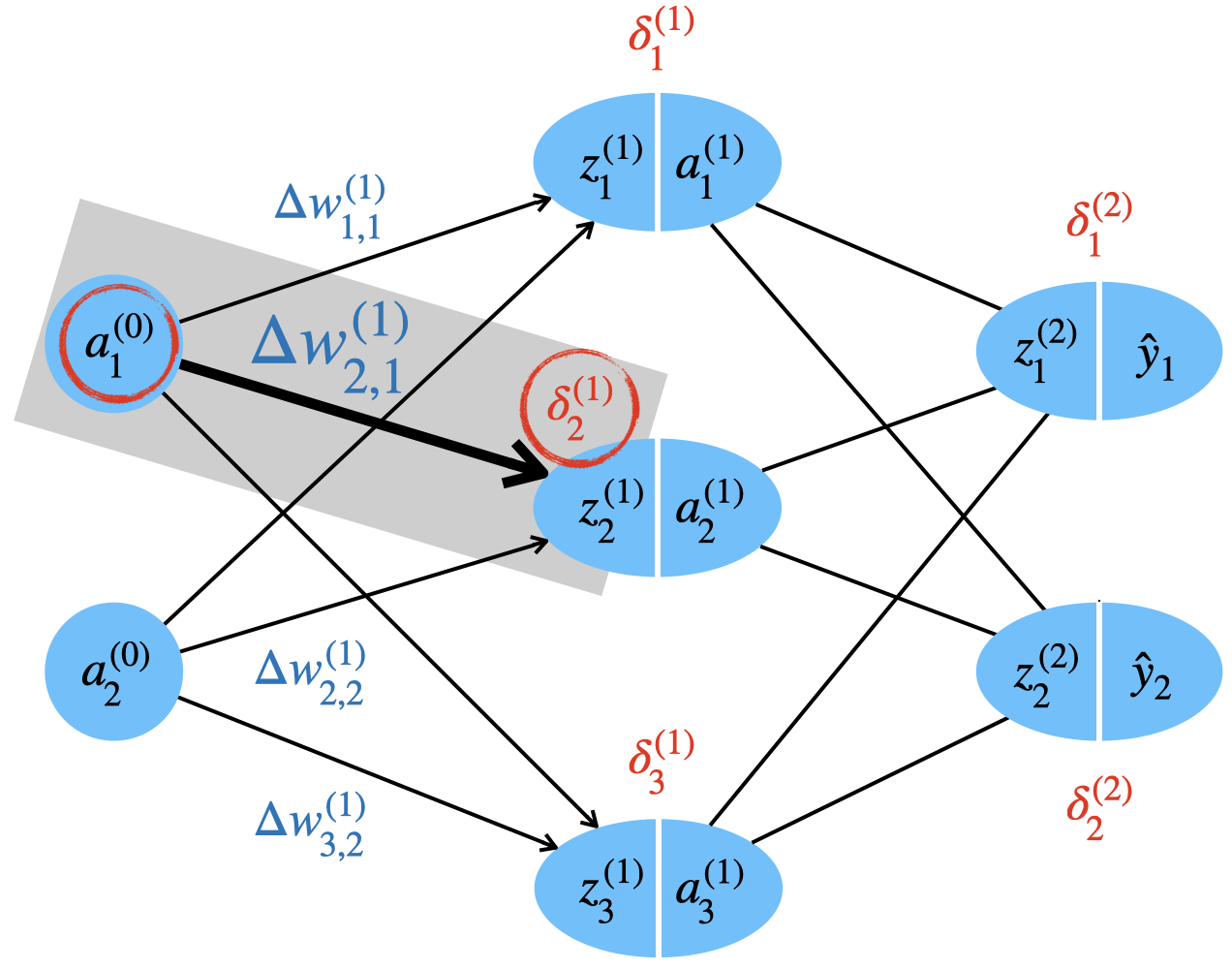
Wir können uns schematisch ansehen, wie für eine Gewichtsänderung \(\Delta w^{(1)}_{2,1}\) sowohl der Fehlerwert des Zielneurons \(\delta^{(1)}_2\) als auch die Aktivierung des Quellneurons \(a^{(0)}_1\) hinzugezogen wird. Die Herleitung zur obigen Formel finden Sie im nächsten Kapitel 7 unter (W).
Für die Bias-Gewichte \(b^{(l)}\) gilt analog:
\[ \Delta b_i^{(l)} = - \frac{\partial J}{\partial b_i^{(l)}} = - \delta_i^{(l)} \]
Wenn man diese Formel mit der obigen vergleicht, kann man sich vorstellen, dass die Aktivierung \(a^{(l-1})\) hier ja immer gleich eins ist. Die Herleitung zu dieser Formel finden Sie im nächsten Kapitel 7 unter (B).
Vektorform
Wenn wir die Berechnungen mit Matrizen durchführen möchten, erstellen wir pro Schicht eine Matrix \(\Delta W^{(l)}\), wobei \(l \in \{1,\ldots,L\}\). Diese Matrizen beinhalten alle Änderungen aller Gewichte. Zusätzlich benötigen wir Vektoren \(\Delta b^{(l)}\) für die Biasneuronen.
Die Matrix kann elegant berechnet werden mit
\[ \label{backprop2}\tag{DelW} \Delta W^{(l)} = - \delta^{(l)} \: (a^{(l-1)})^T \]
Die Vektoren für die Biasgewichte sind ganz einfach:
\[ \label{backprop3}\tag{DelB} \Delta b^{(l)} = - \delta^{(l)} \]
Sanity Check:
Wir möchten (DelW) mit Hilfe unseres Beispielnetzwerks prüfen. Zwischen der mittleren Schicht 1 und der Ausgabeschicht (Schicht 2) haben wir die 2x3-Gewichtsmatrix \(W^{(2)}\) und die entsprechende 2x3-Deltamatrix \(\Delta W^{(2)}\). Jetzt multiplizieren wir den Fehlervektor der Ausgabeschicht (2x1-Matrix) mit dem transponierten Aktivierungsvektor der 3 Neuronen der mittleren Schicht (1x3-Matrix):
\[ \Delta W^{(2)} = - \left( \begin{array}{c} \delta_1^{(2)} \\ \delta_2^{(2)} \end{array} \right) \; ( a_1^{(1)} \; a_2^{(1)} \; a_3^{(1)} ) = - \begin{pmatrix} \delta_1^{(2)} \: a_1^{(1)} & \delta_1^{(2)} \: a_2^{(1)} & \delta_1^{(2)} \: a_3^{(1)} \\ \delta_2^{(2)} \: a_1^{(1)} & \delta_2^{(2)} \: a_2^{(1)} & \delta_2^{(2)} \: a_3^{(1)} \end{pmatrix}\]
Die Ergebnismatrix hat also die Form 2x3, genau wir es für \(\Delta W^{(2)}\) benötigen.
Update mit allen Trainingsbeispielen
Die obige Formel gilt für ein Trainingsbeispiel, wenn man sich die Herleitung ansieht.
Wenn wir den Fehler für Trainingsbeispiel \(k\) mit \(J_k\) bezeichnen, gilt:
\[ \Delta W^{(l), k} = - \frac{\partial J_k}{\partial W^{(l)}} \]
Nun gilt für unsere Fehlerfunktion \(J\), dass der Gesamtfehler die gemittelte Summe der Fehler auf den einzelnen Beispielen ist:
\[ J = \frac{1}{N} \sum_{k=1}^N J_k \]
Dann möchten wir die Änderung für alle Trainingsbeispiele mit Matrix \(D^{(l)}\) ausdrücken:
\[ D^{(l)} := - \frac{\partial J}{\partial W^{(l)}} \]
Jetzt können wir einsetzen und auflösen:
\[ \begin{align*} D^{(l)} &= - \frac{\partial J}{\partial W^{(l)}} \\[2mm] &= - \frac{\partial}{\partial W^{(l)}} \frac{1}{N} \sum_{k=1}^N J_k\\[2mm] &= \frac{1}{N} \sum_{k=1}^N - \frac{\partial J_k}{\partial W^{(l)}} \\[2mm] &= \frac{1}{N} \sum_{k=1}^{N} \Delta W^{(l), k} \end{align*} \]
In der Praxis durchlaufen wir alle Trainingsbeispiele \(1,\ldots , N\), addieren wir alle Deltamatrizen auf und teilen das Ergebnis durch \(N\):
\[ D^{(l)} = \frac{1}{N} \sum_{k=1}^{N} \Delta W^{(l), k} \]
Dann verwenden wir \(D\), um die Gewichte anzupassen:
\[ W^{(l)} := W^{(l)} + \alpha \: D^{(l)} \]
4.2.5 Formeln im Überblick
Hier nochmal alle relevanten Formeln in Vektorschreibweise.
Forward Propagation
Für die Vorwärtsverarbeitung berechnen wir schichtweise den Rohinput \(z\) und die Aktivierung \(a\).
\[ \begin{align} \label{fp1}\tag{Z} z^{(l)} &= W^{(l)} \; a^{(l-1)} + b^{(l)} \\[3mm] \label{fp2}\tag{A} a^{(l)} &= g(z^{(l)}) \end{align} \]
Backpropagation
Für die Rückwärtsverarbeitung berechnen wir rückwärts-schichtweise die Fehlerterme \(\delta\) und die Updates für Gewichtsmatrizen \(\Delta W\) und die Updates für die Bias-Vektoren \(\Delta b\).
\[ \begin{align} \label{bp1}\tag{D'}\delta^{(l)} & = \begin{cases} \hat{y} - y & \mbox{wenn}\quad l = L\\[3mm] (W^{(l+1)})^T \; \delta^{l+1} \odot a^{(l)} \odot (1 - a^{(l)})& \mbox{wenn}\quad l \in \{1, \ldots, L-1\} \end{cases}\\[5mm] \label{bp2}\tag{DelW} \Delta W^{(l)} & = - \delta^{(l)} \: (a^{(l-1)})^T \\[3mm] \label{bp3}\tag{DelB} \Delta b^{(l)} & = - \delta^{(l)} \end{align} \]
4.2.6 Backpropagation-Algorithmus
Wir führen jetzt die vielen Formeln in ein Trainingsverfahren zusammen. Zunächst in der Standardvariante, wo alle Trainingsbeispiele für ein Update durchlaufen werden. Dann in der Mini-Batch-Variante, wo kleinere Teilmengen der Trainingsdaten (Mini-Batches) pro Update durchlaufen werden.
Standardalgorithmus
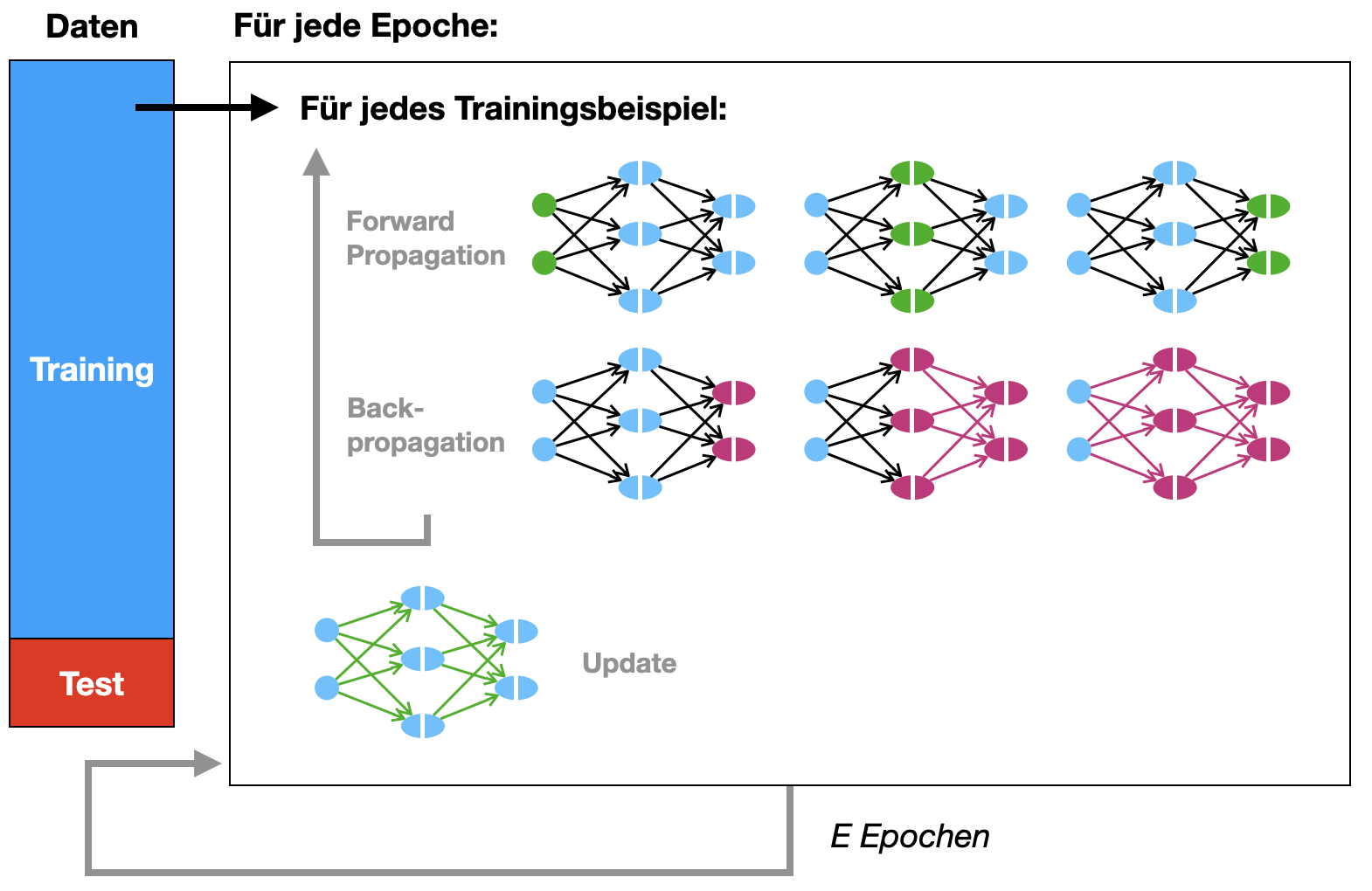
Zunächst der Standardalgorithmus für \(N\) Trainingsbeispiele \((x^k, y^k)\). Hier sehen wir den Ablauf für genau eine Epoche.
- Initialisiere für alle Schichten \(l = 1,\ldots, L\)
- Sammelmatrizen \(D^{(l)}\) mit Nullen
- Sammelvektoren \(B^{(l)}\) mit Nullen
- Führe für alle Trainingsbeispiele \(k = 1, \ldots, N\) aus
(Wir lassen Index \(k\) der Übersichtlichkeit wegen weg.)
- Forward Propagation:
- Setze die Input-Aktivierung auf den Trainingsvektor \(a^{(0)} := x^k\)
- Berechne die Aktivierungen der Schichten: \(a^{(1)}, \ldots, a^{(L)} = \hat{y} \quad\) (Z & A)
- Backpropagation:
- Berechne alle Fehler in der Reihenfolge \(\delta^{(L)}, \ldots, \delta^{(2)}, \delta^{(1)} \quad\) (D)
- Für alle Schichten \(l\) sammle die \(\Delta W\) und \(\Delta b\) ein (gemäß DelW & DelB):
- \(D^{(l)} := D^{(l)} - \delta^{(l)} \: (a^{(l-1)})^T\)
- \(B^{(l)} := B^{(l)} - \delta^{(l)}\)
- Update für alle Schichten \(l\)
- alle Gewichtsmatrizen mit \(W^{(l)} := W^{(l)} + \alpha \: \frac{1}{N} D^{(l)}\)
- alle Biasvektoren mit \(b^{(l)} := b^{(l)} + \alpha \: \frac{1}{N} B^{(l)}\)
Schematisch kann man sich das wie folgt vorstellen:
Mini-Batch
Die obige Variante ist klassische Batch-Training. Bei Mini-Batch würde man in Schritt 2 nicht alle \(N\) Beispiele durchlaufen, sondern nur einen Teil davon, und dann Schritt 3 (Updates) durchführen. Die Epoche ist dann aber noch nicht zu Ende. Erst würde man alle Mini-Batches durchlaufen (und jeweils die Gewichte anpassen).
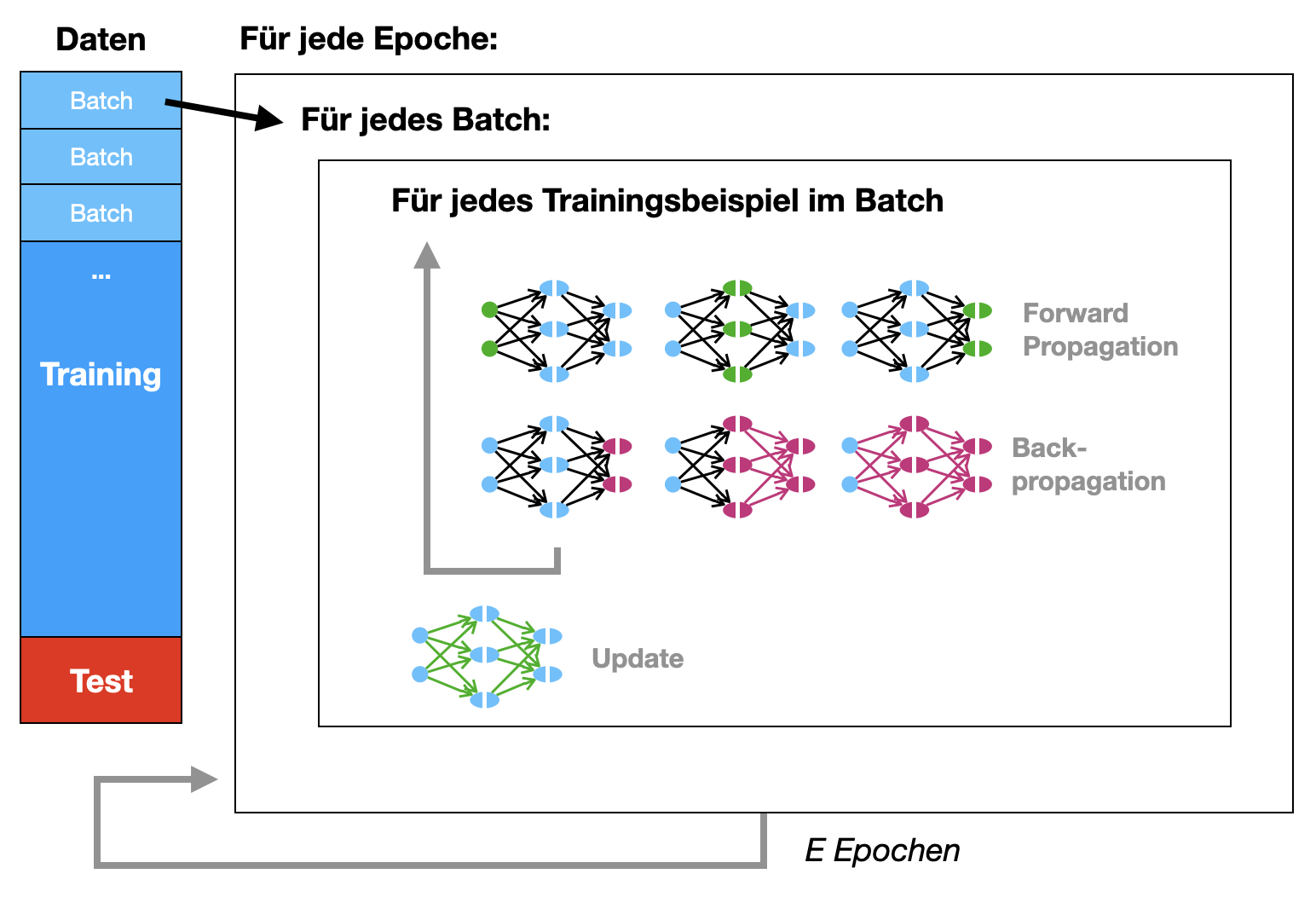
Wir definieren Mini-Batch als Algorithmus. Die Trainingsdaten \(T\) seien aufgeteilt auf \(M\) Teilmengen \((T_1, \ldots, T_M)\). Wir skizzieren hier den Algorithmus, der ansonsten analog zu dem Standardalgorithmus ist.
Für jede Epoche:
Für jede Teilmenge \(T_j \quad (j = 1, \ldots, M)\)
- Initialisiere Sammelmatrizen \(D^{(l)}\) und Sammelvektoren \(B^{(l)}\) mit Nullen
- Für alle Trainingsbeispiele \((x, y) \in T_j\):
- Setze \(a^{(0)} := x\)
- Berechne alle Aktivierungen \(a^{(1)}, \ldots, a^{(L)} = \hat{y}\) (Forward Propagation)
- Berechne alle Fehler \(\delta^{(L)}, \ldots, \delta^{(2)}, \delta^{(1)}\) (Backpropagation)
- Erhöhe alle \(D^{(l)}\) und \(B^{(l)}\)
- Update: Passe die Gewichtsmatrizen \(W^{(l)}\) und die Biasvektoren \(b^{(l)}\) für alle Schichten \(l\) an
Auch hier als Ablaufschema:
Siehe auch die Videos von Andrew Ng: Mini Batch Gradient Descent und Understanding Mini-Batch Gradient Descent
Batch und Mini-Batch
In unserem Kontext bedeutet Batch-Training, dass alle Traningsbeispiele in einem Rutsch durchlaufen werden (und dann ein Update durchführt) und Mini-Batch-Training, dass man die Trainingsbeispiele in kleinere Einheiten unterteilt und für jede dieser kleineren Einheiten ein Update durchführt. Diese kleineren Einheiten nennt man auch Batches und die Anzahl der Trainingsbeispiele in einem Batch nennt man batch size. Heutzutage ist praktisch jedes Training vom Typ Mini-Batch, aber man muss etwas vorsichtig sein mit den Begriffen.
4.2.7 Parallele Verarbeitung mehrerer Trainingsbeispiele
In der Regel stellt man sich die Verarbeitung so vor, dass man zunächst das erste Trainingsbeispiel verwendet, um eine komplette Forward Propagation zu berechnen und dann das nächste Beispiel usw. Es stellt sich aber heraus, dass es deutlich effizienter ist, erst für alle Trainingsbeispiele die Ausgabe der ersten Schicht zu berechnen, dann für alle Beispiele die zweite Schicht usw.
Seien \((x^k, y^k)\) die Trainingsbeispiele, wobei \(k \in \{1,\ldots, N\}\).
Vorwärtsverarbeitung für ein Trainingsbeispiel
Sehen Sie sich noch einmal das Beispielnetz in Abbildung 4.1 an. Betrachten wir den ersten Verarbeitungsschritt von von der Eingabe zu Schicht \(1\) (ohne Bias):
\[ z^{(1)} = W^{(1)} \; x \]
\(W^{(1)}\) ist eine \(3\times 2\) Matrix und \(x\) ist eine \(2\times 1\) Matrix, so dass das Ergebnis \(z^{(1)}\) eine \(3\times 1\) Matrix ist. Wir lassen hier den Index für das Trainingsbeispiel weg:
\[ \label{ein_sample}\tag{a} \begin{pmatrix} w_{1,1}^{(1)} & w_{1,2}^{(1)} \\ w_{2,1}^{(1)} & w_{2,2}^{(1)} \\ w_{3,1}^{(1)} & w_{3,2}^{(1)} \end{pmatrix} \left( \begin{array}{c} x_1 \\ x_2 \end{array} \right) = \left( \begin{array}{c} z_1^{(1)} \\ z_2^{(1)} \\ z_3^{(1)} \end{array} \right) \]
Wir könnten jetzt die Aktivierung \(a^{(1)}\) berechnen und dann mit \(W^{(2)}\) die nächste Schicht berechnen. Aber bei mehreren Trainingsbeispielen geht man anders vor.
Vorwärtsverarbeitung für mehrere Trainingsbeispiele
Wir könnten also für das Bespiel oben (a) die nächste Schicht für das aktuelle Trainingsbeispiel berechnen oder (b) wir könnten für das nächste Trainingsbeispiel auch erstmal die erste Schicht berechnen. Beides wäre möglich, da wir davon ausgehen, dass sich die Gewichte nicht ändern. Wir können also im Extremfall für alle Trainingsbeispiele erst einmal die Ergebnisse der ersten Schicht berechenen. Wir müssen natürlich alle diese Ergebnisse speichern, damit wir im nächsten Schritt für alle Trainingsbeispiele die Ergebnisse an der zweiten Schicht berechnen können.
Ähnlich wie beim Perzeptron in Abschnitt 3.4 bilden wir aus den Eingabevektoren aller \(N\) Trainingsbespiele eine \(2\times N\) Matrix \(X\). Das heißt, jedes Trainingsbeispiel bekommt eine Spalte in der Matrix \(X\).
Implementations-Hinweis
Bei einer Implementierung kann es sinnvoller sein, die Trainingsbeispiele zeilenweise anzulegen. Wenn man in Python die Trainingsbeispiele (also die Feature-Vektoren \(x\)) in einer 2-dimensionalen Liste x_train vorliegen hat, dann bezeichnet entsprechend der erste Index immer das Trainingsbeispiel, also bekommt man zum Beispiel mit x_train[0] das erste Trainingsbeispiel. Würde man die Beispiele in Spalten anlegen, müsste man auf das erste Trainingsbeispiel mit x_train[:,0] zugreifen. Beim Programmieren sind Spalten also eher unpraktisch, in der Mathematik sind Spalten schöner…
Wir müssen hier einen Index für die Trainingsbeispiele (von \(1\) bis \(N\)) hinzufügen. Zur Erinnerung: der obere Index ohne Klammer gibt die Nummer des Trainingsbeispiels an. Sie sehen gut, dass die Trainingsbeispiele in Spalten nebeneinander stehen:
\[ X = \begin{pmatrix} x_1^{1} & \ldots & x_1^{N} \\ x_2^{1} & \ldots & x_2^{N} \end{pmatrix} \]
Wir schauen uns die Rechnung von oben an, wobei wir das einzelne Trainingsbeispiel \(x\) durch die Matrix \(X\) mit allen Trainingsbeispielen ersetzen (zur Erinnerung: der hochgestellte Index mit Klammern gibt die Schicht an):
\[ W^{(1)} \; X = \begin{pmatrix} w_{1,1}^{(1)} & w_{1,2}^{(1)} \\ w_{2,1}^{(1)} & w_{2,2}^{(1)} \\ w_{3,1}^{(1)} & w_{3,2}^{(1)} \end{pmatrix} \begin{pmatrix} x_1^{1} & \ldots & x_1^{N} \\ x_2^{1} & \ldots & x_2^{N} \end{pmatrix} = \begin{pmatrix} z_1^{(1), 1} & \ldots & z_1^{(1), N} \\ z_2^{(1), 1} & \ldots & z_2^{(1), N} \\ z_3^{(1), 1} & \ldots & z_3^{(1), N} \end{pmatrix} = Z^{(1)} \]
Vergleichen Sie diese Rechnung mit der Rechung (\(\ref{ein_sample}\)). Was Sie hier sehen ist, dass wir eine Matrix \(Z^{(1)}\) erhalten, die die Roheingaben aller \(N\) Trainingsbeispiele für Schicht \(1\) erhält, die sich aus der “gleichzeitigen” Verarbeitung aller Trainingsvektoren \(x^1, \ldots , x^N\) ergibt. Und das alles mit einer einzigen Matrixmultiplikation. Es ist, als hätten wir mit \(N\) Netzen gleichzeitig die \(N\) Trainingseingaben verrechnet. Man beachte aber, dass dies nur zulässig ist, wenn bei allen Berechnungen die gleichen Gewichte gelten.
In gleicher Weise kann man die weiteren Schichten verarbeiten (nicht vergessen, die Aktivierungsfunktion \(f\) noch auf alle Elemente von \(Z^{(1)}\) anzuwenden, dann weiter zur Schicht \(2\)), um schließlich die Gesamtausgabe in einer Matrix \(\hat{Y}\) zu erhalten. Die Spalten von \(\hat{Y}\) entsprechen den Ausgabevektoren \(\hat{y}^1,\ldots , \hat{y}^N\) für alle \(N\) Trainingsbeispiele.
Berücksichtigung des Bias-Gewichtsvektors
Wir haben oben den Bias-Gewichtsvektor ignoriert. Bei einem Trainingsbeispiel addieren wir eigentlich noch Vektor \(b^1\):
\[ \begin{pmatrix} w_{1,1}^{(1)} & w_{1,2}^{(1)} \\ w_{2,1}^{(1)} & w_{2,2}^{(1)} \\ w_{3,1}^{(1)} & w_{3,2}^{(1)} \end{pmatrix} \left( \begin{array}{c} x_1 \\ x_2 \end{array} \right) + \left( \begin{array}{c} b_1^1 \\ b_2^1 \\ b_3^1 \end{array} \right) = \left( \begin{array}{c} z_1^{(1)} \\ z_2^{(1)} \\ z_3^{(1)} \end{array} \right) \]
Wenn wir die Eingabevektoren zur Matrix \(X\) zusammenfassen, haben wir folgende Rechnung ohne Bias:
\[ \begin{pmatrix} w_{1,1}^{(1)} & w_{1,2}^{(1)} \\ w_{2,1}^{(1)} & w_{2,2}^{(1)} \\ w_{3,1}^{(1)} & w_{3,2}^{(1)} \end{pmatrix} \begin{pmatrix} x_1^{1} & \ldots & x_1^{N} \\ x_2^{1} & \ldots & x_2^{N} \end{pmatrix} = \begin{pmatrix} z_1^{(1), 1} & \ldots & z_1^{(1), N} \\ z_2^{(1), 1} & \ldots & z_2^{(1), N} \\ z_3^{(1), 1} & \ldots & z_3^{(1), N} \end{pmatrix} \]
Die Ergebnismatrix hat \(N\) Spalten, eben eine Spalte für jedes Trainingsbeispiel. Man kann hier keinen Vektor addieren. Um den Bias hinzuzufügen, müsste man eigentlich eine Matrix \(B\) addieren, wo der Bias-Gewichtsvektor \(N\)-mal kopiert in \(N\) Spalten vorliegt:
\[ \begin{pmatrix} w_{1,1}^{(1)} & w_{1,2}^{(1)} \\ w_{2,1}^{(1)} & w_{2,2}^{(1)} \\ w_{3,1}^{(1)} & w_{3,2}^{(1)} \end{pmatrix} \begin{pmatrix} x_1^{1} & \ldots & x_1^{N} \\ x_2^{1} & \ldots & x_2^{N} \end{pmatrix} + \begin{pmatrix} b_1^1 & \ldots & b_1^1 \\ b_2^1 & \ldots & b_2^1 \\ b_3^1 & \ldots & b_3^1 \end{pmatrix} = \begin{pmatrix} z_1^{(1), 1} & \ldots & z_1^{(1), N} \\ z_2^{(1), 1} & \ldots & z_2^{(1), N} \\ z_3^{(1), 1} & \ldots & z_3^{(1), N} \end{pmatrix} \]
Technisch gesehen gibt es zwei Möglichkeiten, das zu tun, ohne tatsächlich die Matrix \(B\) zu konstruieren (was eventuell wertvolle Rechenzeit kostet).
Option 1: Man erweitert die Matrizen \(W\) und \(X\) wie folgt:
\[ \begin{pmatrix} w_{1,1}^{(1)} & w_{1,2}^{(1)} & b_1 \\ w_{2,1}^{(1)} & w_{2,2}^{(1)} & b_2 \\ w_{3,1}^{(1)} & w_{3,2}^{(1)} & b_3 \end{pmatrix} \begin{pmatrix} x_1^{1} & \ldots & x_1^{N} \\ x_2^{1} & \ldots & x_2^{N} \\ 1 & \ldots & 1 & \end{pmatrix} = \begin{pmatrix} z_1^{(1), 1} & \ldots & z_1^{(1), N} \\ z_2^{(1), 1} & \ldots & z_2^{(1), N} \\ z_3^{(1), 1} & \ldots & z_3^{(1), N} \end{pmatrix} \]
Option 2: Man nutzt das Broadcasting in NumPy, so dass Vektor \(b\) auf korrekte Weise \(N\)-mal kopiert wird bei der Addition:
\[ \begin{pmatrix} w_{1,1}^{(1)} & w_{1,2}^{(1)} \\ w_{2,1}^{(1)} & w_{2,2}^{(1)} \\ w_{3,1}^{(1)} & w_{3,2}^{(1)} \end{pmatrix} \begin{pmatrix} x_1^{1} & \ldots & x_1^{N} \\ x_2^{1} & \ldots & x_2^{N} \end{pmatrix} \oplus \left( \begin{array}{c} b_1 \\ b_2 \\ b_3 \end{array} \right) = \begin{pmatrix} z_1^{(1), 1} & \ldots & z_1^{(1), N} \\ z_2^{(1), 1} & \ldots & z_2^{(1), N} \\ z_3^{(1), 1} & \ldots & z_3^{(1), N} \end{pmatrix} \]
Wir haben das Broadcasting mit dem Symbol \(\oplus\) angedeutet. Die Bedeutung ist, dass der Vektor \(b\) auf jede Spalte der links stehenden Matrix addiert wird.