11 Computer Vision
In diesem Kapitel geht es darum, Konvolutionsnetze im Kontext des Maschinellen Sehens (Computer Vision) zu betrachten. Konkret geht es um Objekterkennung, wo wir sowohl die Klasse eines Objekts als auch seine Position im Bild erkennen wollen. Wir lernen, wie wir den Typ und den Ort von Objekten in Bildern mit Hilfe von Konvolutionsnetzen erkennen. Wir konzentrieren uns dabei auf den populären YOLO-Algorithmus.
Objekterkennung, Bounding Box, Sliding-Window-Methode, IOU, Non-Max-Suppression, YOLO, R-CNN
Nutzen Sie die Lernziele, um Ihr Wissen zu überprüfen:
- Sie verstehen, wie man von Klassifikation zur Objekterkennung mit Hilfe von Bounding Boxes übergeht
- Sie können die Sliding-Window-Methode erklären
- Sie verstehen, wie man die Sliding-Window-Methode mit Hilfe von Konvolutionen umsetzt
- Sie können IOU erklären und berechnen
- Sie können den Non-Max-Suppression Algorithmus erklären
- Sie kennen den Sinn von Ankerboxen
- Sie können das YOLO-Verfahren mit Hilfe der Teilmechanismen erklären
- Sie kennen den prinzipiellen Unterschied zwischen YOLO und R-CNN
11.1 Objekterkennung
Nachdem wir uns CNNs genauer angesehen haben, möchten wir in diesem Kapitel CNNs im Kontext des Maschinellen Sehens bzw. Computer Vision betrachten. Eine zentrale Aufgabe in diesem Bereich ist die Objekterkennung.
Ein Bild ist zunächst mal nur eine Matrix aus Pixeln. Ob auf dem Bild ein Objekt oder ein Mensch zu sehen ist, erfordert die Kompetenz der “Objekterkennung”. Wir fassen zunächst mal Menschen und Tiere auch unter den Begriff Objekte.
Man kann das Thema in verschiedene Fragen gliedern:
- Existenz: Ist auf dem Bild ein Objekt (oder eine Person) abgebildet oder nicht?
- Typ/Kategorie: Wenn ja, um welchen Objekt-Typ handelt es sich (z.B. Auto, Fahrrad, Mensch, Verkehrsschild)? Diese Typologie ist natürlich abhängig vom Anwendungsszenario.
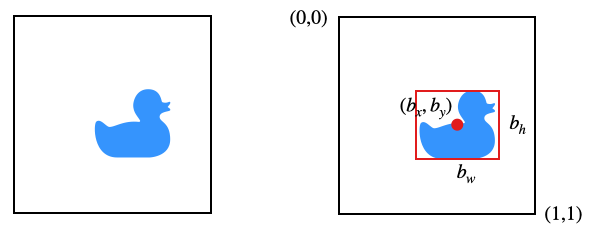
In den folgenden Beispiel sehen wir eine Ente im Bild. Um den Ort der Ente anzugeben, benutzen wir eine Bounding Box, das ist das kleinste mögliche Rechteck, bei dem das Objekt noch vollständig enthalten ist. Die Bounding Box können wir z.B. über den Mittelpunkt \((b_x, b_y)\) und seine Höhe \(b_h\) und Breite \(b_w\) vollständig spezifizieren.
Jetzt können wir ein CNN definieren, das Bilder wie das obige bekommt und einen Output \(y\) liefert.
Wir nehmen mal für unser Beispiel an, dass wir drei Kategorien von Objekten erkennen möchten (Mensch, Auto, Ente), dann hat Output \(y\) folgende Komponenten:
- \(p_c\): zeigt an, ob sich ein Objekt auf dem Bild befindet (1) oder nicht (0)
- \(b_x, b_y, b_h, b_w\): Position (Mittelpunkt) und Ausdehnung der Bounding Box um das Objekt
- \(c_1, c_2, c_3\): zeigt an, ob das Objekt von Kategorie 1, 2 oder 3 ist (One-Hot-Encoding)
Wir haben implizit eine vierte Kategorie für “Hintergrund”.
Der Output \(y\) ist in unserem Beispiel also ein Vektor der Länge 8:
\[ y= \left( \begin{array}{c} p_c \\ b_x \\ b_y \\ b_h \\ b_w \\ c_1 \\ c_2 \\ c_3 \end{array}\right) = \left( \begin{array}{c} 1 \\ 0.6 \\ 0.55 \\ 0.3 \\ 0.4 \\ 0 \\ 0 \\ 1 \end{array}\right) \]
Wichtig ist, dass im Fall \(p_c = 0\) alle anderen Werte egal sind und nicht notwendigerweise Null sein müssen. Wir schreiben das dann so:
\[ \left( \begin{array}{c} 0 \\ \ldots \\ \ldots \\ \ldots \\ \ldots \\ \ldots \\ \ldots \\ \ldots \end{array}\right) \]
Wenn wir ein CNN trainieren wollen, benötigen wir also Trainingsdaten \((x_k, y_k)\), wo für jedes Bild obiger Vektor zur Verfügung steht. Diese Informationen werden in der Regel von Menschen von Hand kodiert, man nennt das auch das Annotieren Bilddaten. Das ist sehr aufwändig, kann aber durch Mechanismen wie automatische Vorverarbeitung plus menschliche Korrektur oder durch Crowdsourcing erleichtert werden.
Beachten Sie, dass es sich hier um eine Mischung aus Klassifikation und Regression handelt. Die Komponente \(p_c\) bildet eine binäre Klassifikation ab, d.h. der Zielwert ist immer entweder 0 oder 1. Die Komponenten \(b_x, b_y, b_h, b_w\), die die Bounding Box abbilden, sind aber kontinuierliche Werte. Das heißt, dass diese Komponenten ein Regressionsszenario repräsentieren, ähnlich wie das Problem, für Hausdaten (Quadratmeter) den Kaufpreis (kontinuierlicher Wert) vorhersagen zu wollen. Die Komponenten \(c_1, c_2, c_3\) wiederum bilden ein Szenario der Mehrklassen-Klassifikation ab.
Dies hat Auswirkungen auf die Fehlerfunktion. Da man für Regression oft den quadratischen Fehler nimmt, ist dies in diesem Fall eine adäquate Wahl (\(\hat{y}\) steht wie immer für den errechneten Wert, \(y\) für den korrrekten Wert). Da die erste Komponente \(y_1\) die Kategorie abbildet (\(p_c\)), müssen wir aber unterscheiden
\[ L(\hat{y}, y) = \begin{cases} (\hat{y}_1 - y_1)^2 + (\hat{y}_2 - y_2)^2 + \ldots + (\hat{y}_8 - y_8)^2 & \quad \text{falls } y_1 = 1 \\[3mm] (\hat{y}_1 - y_1)^2 & \quad \text{sonst} \end{cases} \]
Das heißt also, dass für \(p_c = 0\, ( = y_1)\) nur der Fehler der ersten Stelle genommen wird und die Bounding-Box-Angaben ignoriert werden.
11.2 Sliding-Window-Methode
Die oben geschilderte Methode mit der Ausgabe der Bounding Box hat den Nachteil, dass das zu erkennende Objekt häufig nur einen kleinen Teil des Bildes einnimmt. Man sollte annehmen, dass die Daten zu einem weniger effizienten Training führen. Daher verwendet man - auch in der klassischen Bildverarbeitung - die Sliding-Window-Methode. Ein weiterer Nachteil ist, dass man die Methode nicht gut auf mehrere Objekte erweitern kann. Man müsste für jedes weitere potentielle Objekt sechs weitere Komponenten hinzufügen (für Existenz, Bounding-Box und Klasse).
11.2.1 Konventionelle Methode
In der Sliding-Window-Methode gehen wir davon aus, dass wir ein Objekt gut erkennen können, sofern es relativ groß im Bild ist. Als Beispiel nehmen wir an, wir hätten ein CNN, dass dies leistet. Es wurde trainiert mit vielen Bildern von Autos \((x_k, y_k)\), wo \(y_k = 1\), falls ein Auto auf dem Bild ist und sonst \(y_k = 0\).
Gitter
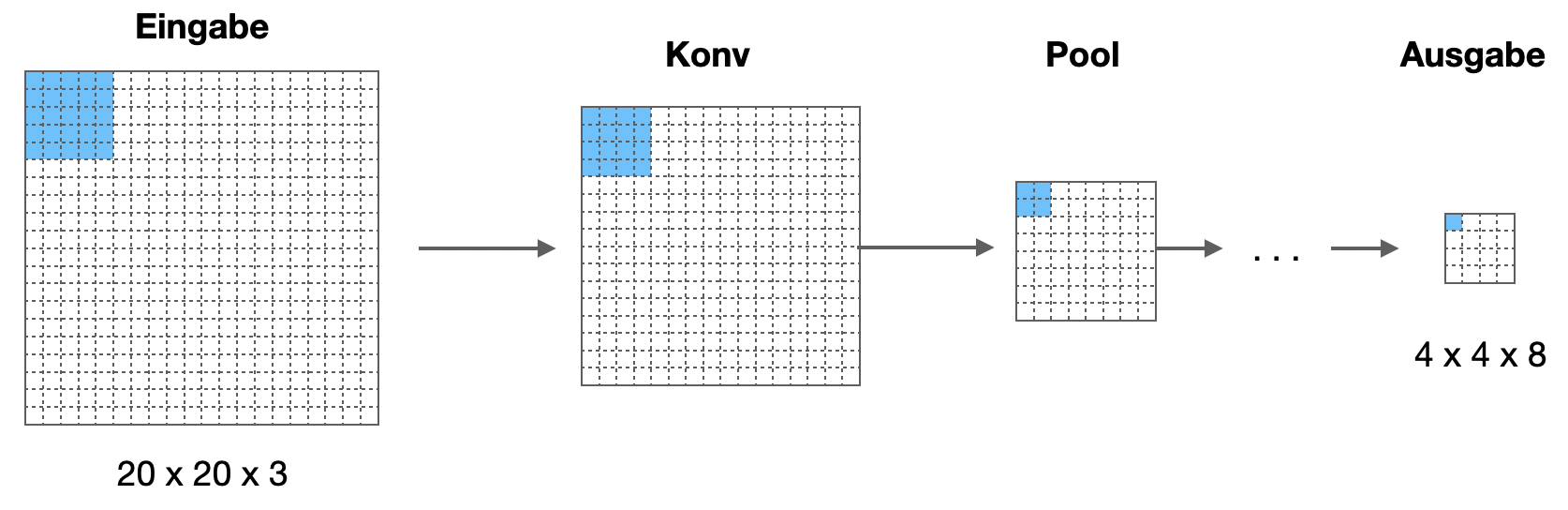
Wenn wir ein Bild vor uns haben, auf dem wir eventuell mehrere Autos vor uns haben, zerteilen wir das Bild in ein Gitter und wenden auf jede Zelle unser CNN an, um herauszufinden, ob dort ein Auto ist. Die jeweils aktuelle Zelle ist unser Sliding Window. In der Abbildung sehen wir ein 4x4-Gitter und die ersten zwei Schritte unseres Sliding Window. Am “Zeilenende” beginnt das Sliding Window wieder von vorn in der nächsten Zeile.
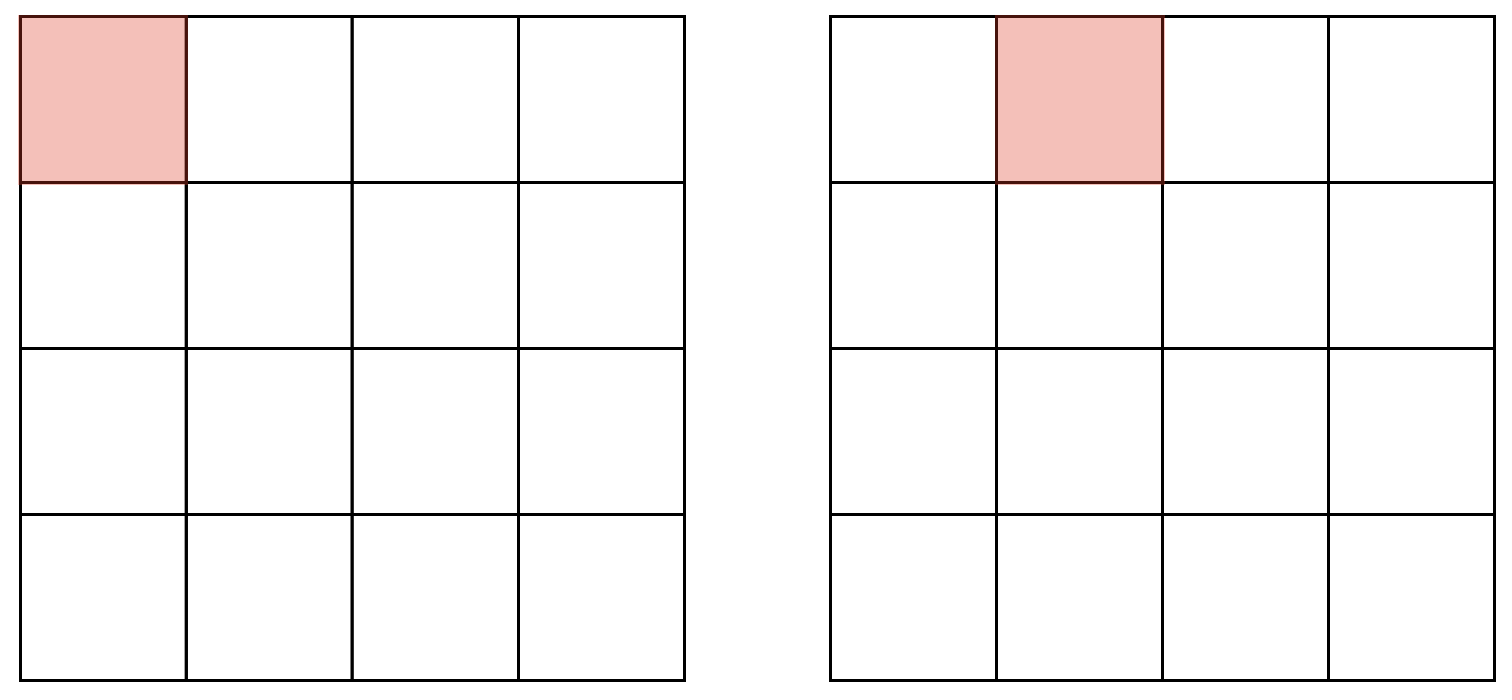
Beachten Sie, dass das Gitter oben nicht Pixel zeigt. Stattdessen wird z.B. ein 100x100-Bild in 25x25 Pixel große Teile zerlegt.
Wir können die Gittergröße verstellen, im Beispiel haben wir ein 4x4-Gitter gewählt, üblich sind Größen wie 19x19.
Stride
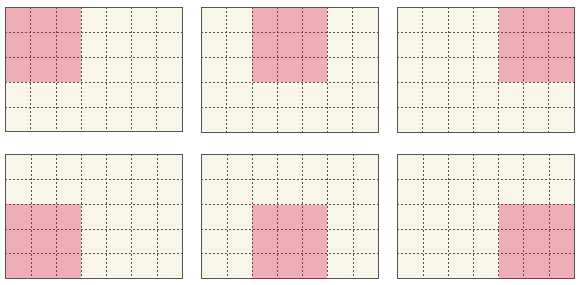
Die zweite Einstellung ist der Stride. Wir könnten das Sliding Window z.B. nur um eine halbe Länge nach rechts schieben (damit kommt es zur Überlappung) oder um 1,5 Längen (damit bleiben Flächen un-bearbeitet). Im weiteren werden wir aber wie abgebildet einen Stride so wählen, dass es keine Überlappungen gibt und das Sliding Window alle Bereiche erfasst.
Wenn wir uns das auf Pixelebene ansehen, benötigen wir nicht unbedingt die Idee des Gitters, sondern definieren nur die Größe des Sliding Window und den Stride. In der Abbildung unten sehen wir ein Sliding Window, das sich mit Stride 2 über das Bild bewegt.
Rechenaufwand
Der Nachteil dieser Methode ist der hohe Rechenaufwand. Für jede Position des Sliding Window muss eine Berechnung durchgeführt werden. Das ist problematisch, da ein CNN mehr Verarbeitungszeit benötigt als viele konventionelle Bildverarbeitungsmethoden. Eine Lösung ist die Konvolutionsvariante der Sliding-Window-Methode.
11.2.2 Konvolutionsmethode
Jetzt möchten wir die Sliding-Window-Methode in ein CNN einarbeiten (Sermanet et al. 2014). Dazu müssen wir uns ein Beispiel-CNN anschauen. Ein Eingabe wählen wir eine kleine Bildgröße von 14x14x3 für unser Beispiel. Die Ausgabe besteht aus 4 Neuronen mit Softmax-Aktivierung.
Die Ausgabe könnte für die vier Kategorien stehen: 0 = Mensch, 1 = Auto, 2 = Radfahrer, 3 = Hintergrund.
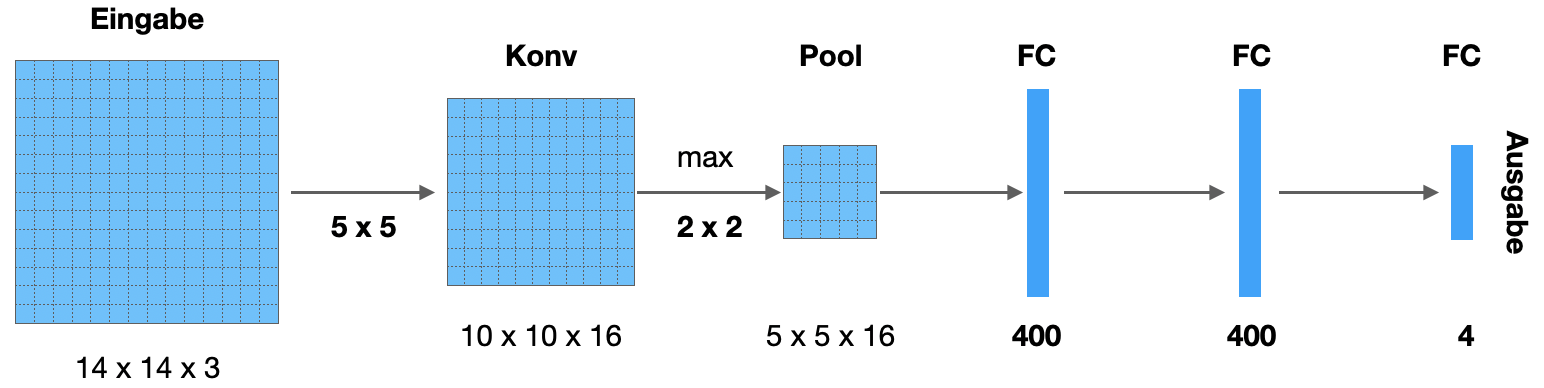
Äquivalenz FC-Schicht und Konvolutionsschicht
In einem ersten Schritt zeigen wir, wie wir die FC-Schichten in KonvSchichten umwandeln können. Schauen Sie auf die hinteren Schichten “Konv (FC)”.
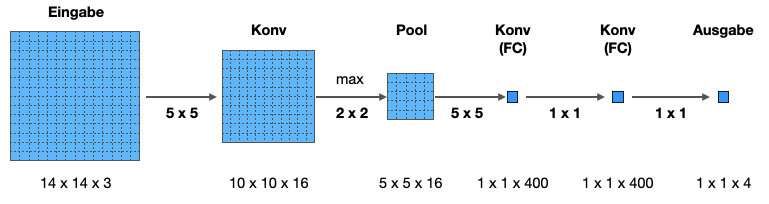
Betrachten wir die erste Konv/FC-Schicht. Wir haben 5x5x16 Neuronen, die hineingehen, und (ursprünglich) eine FC-Schicht mit 400 Neuronen. In der Abbildung oben haben wir die FC-Schicht durch eine KonvSchicht ersetzt, die mit 400 Filtern (5x5) arbeitet. Ist das äquivalent zu der FC-Schicht? Kann man also eine FC-Schicht mit 400 Neuronen durch eine KonvSchicht mit 400 Filtern der Größe 5x5 ersetzen?
Als Beispiel nehmen wir etwas kleinere Zahlen. Die Eingangsmatrix sei 5x5x3 groß. Wir zeigen, dass eine FC-Schicht mit 8 Neuronen äquivalent ist zu einer KonvSchicht mit 8 Filtern der Größe 5x5 und somit einer Ausgabe der Form 1x1x8. Wir benutzen kein Padding (valid):
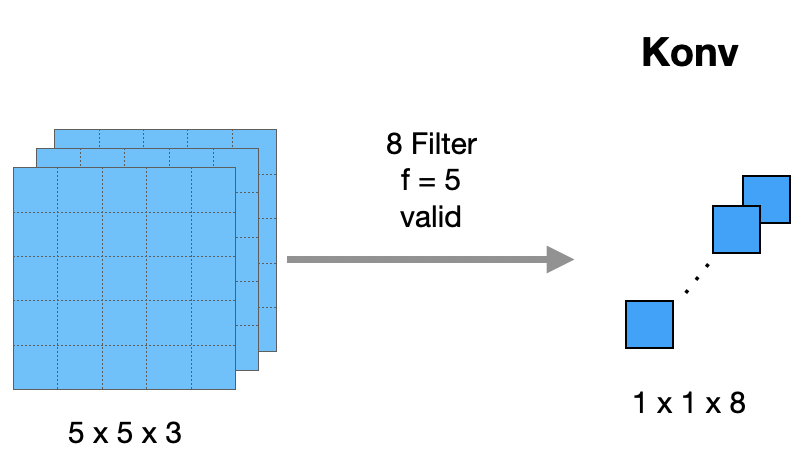
Was natürlich direkt auffällt: Die Filter werden nicht “bewegt”, weil sie genauso groß sind wie die Eingabe. Darin liegt tatsächlich der “Trick”.
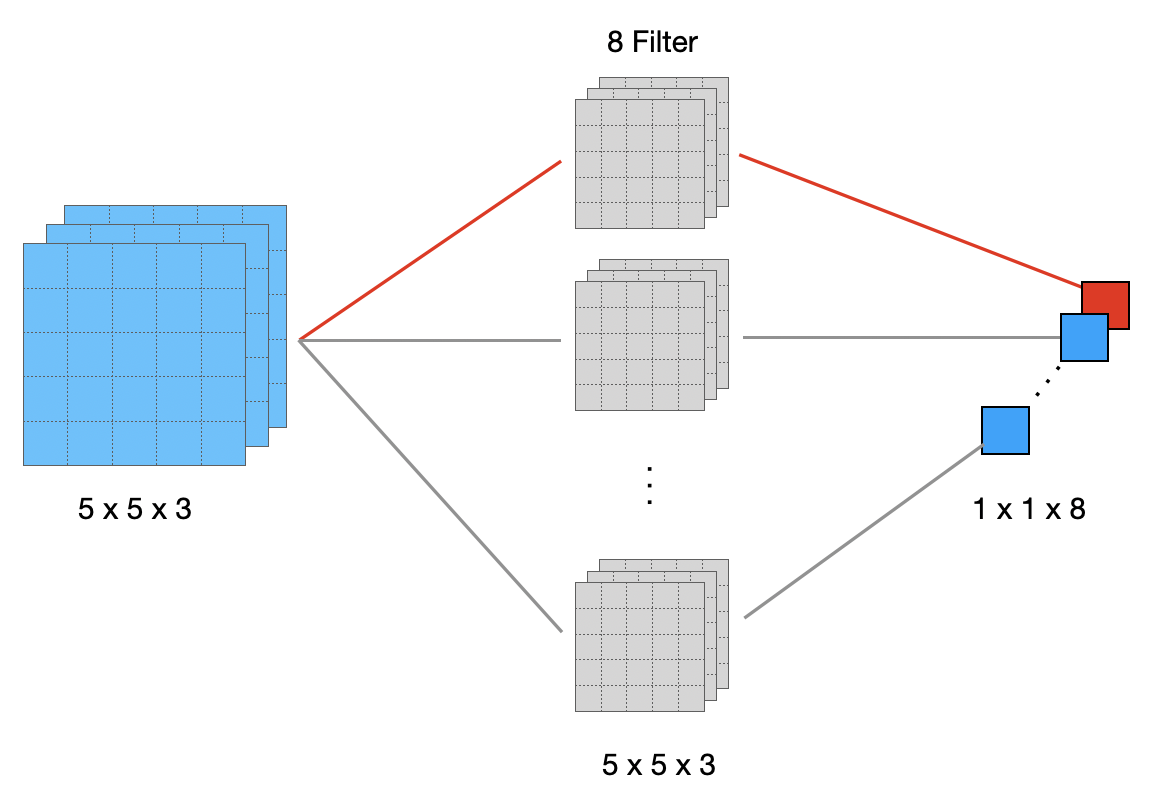
Aber von vorn: In einer FC-Schicht ist jedes Ausgangsneuron mit jedem Eingangsneuron über ein eigenes Gewicht verbunden. Unten sehen wir die 8 Filter. Betrachten wir das erste Ausgangsneuron (rot). Dies wird berechnet durch die gewichtete Summe aller 75 Eingangsneuronen (5x5x3), wobei die 75 Gewichte in dem ersten Filter (grau) stecken. Gleiches gilt für die restlichen Ausgangsneuronen. Insgesamt gibt es 8 * 75 = 600 Gewichte.
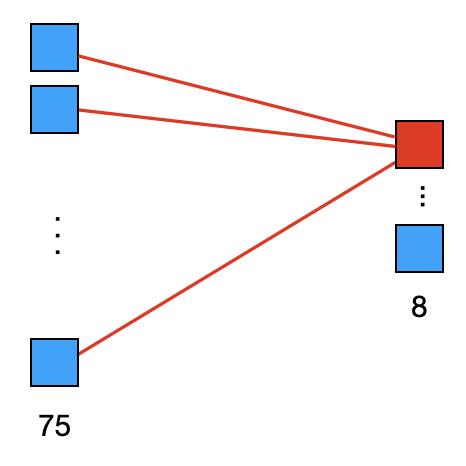
Betrachten wir nochmal eine FC-Schicht mit linearisierten Eingangsneuronen. Die Eingangsmatrix wird zu 75 Neuronen linearisiert. Es gibt 8 Ausgangsneuronen. Sie sehen in der Abb. unten wieder das erste Neuron, dass mit 75 Eingangsneuronen über 75 Gewichte verbunden ist. Gleiches gilt für die restlichen Neuronen, macht also 8 * 75 = 600 Gewichte.
Ich hoffe, das überzeugt Sie, dass die erste FC-Schicht in eine KonvSchicht auf die dargestellte Weise umgewandelt werden kann.
Wenden wir uns der zweiten FC-Schicht zu. Hier hatten wir ursprünglich 400 Eingangsneuronen und 400 Ausgangsneuronen. Wir vereinfachen das wieder auf ein Beispiel mit 8 Eingangsneuronen und 4 Ausgangsneuronen. Dort hätten wir bei einer FC-Schicht also 8 * 4 = 32 Gewichte.
Sehen wir uns diese Schicht in der KonvSchicht-Version an. Wir haben als Eingang eine 1x1x8-Matrix und als Ausgang eine 1x1x4-Matrix. Die KonvSchicht wendet 4 Filter (grau) der Größe 1x1x8 an. Wir betrachten wieder das erste Ausgangsneuron:
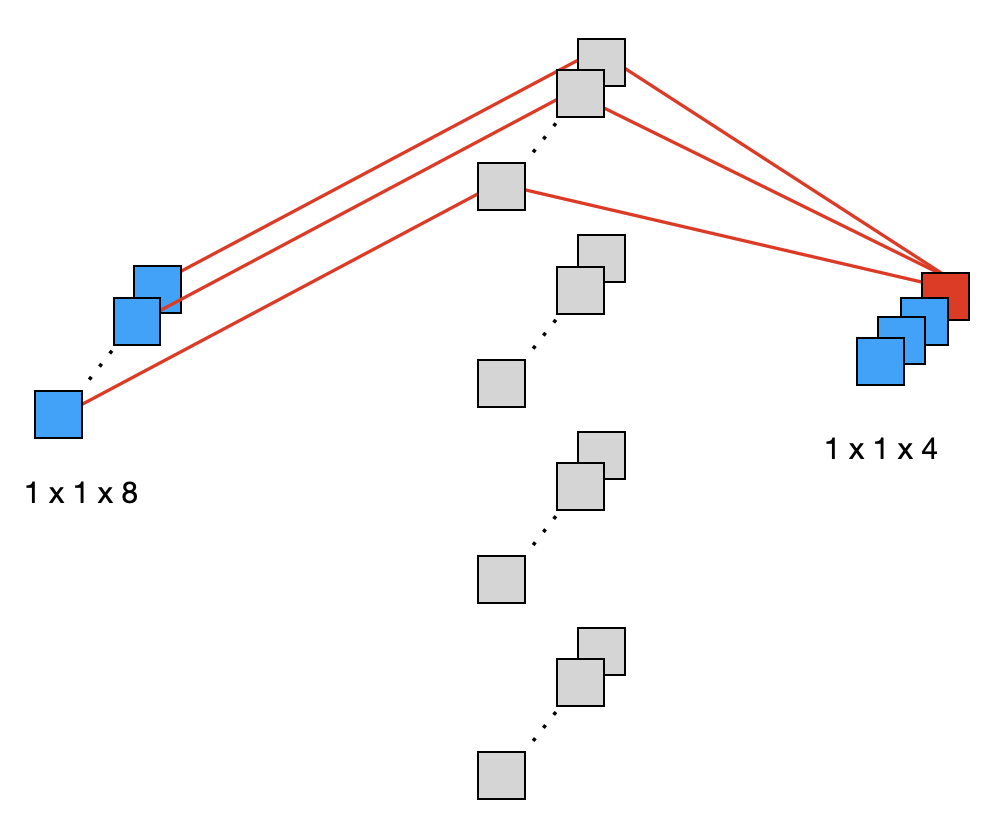
Wir sehen, dass das erste Ausgangsneuron mit allen 8 Eingangsneuronen über 8 eigene Gewichte, die im ersten Filter stecken, verbunden ist. Insgesamt gibt es 4 * 8 = 32 Gewichte.
Sliding Window als Konvolution
Jetzt nehmen wir an, dass das CNN oben für ein 14x14-Bild eine Klassifizierung vornehmen kann. Das eigentliche Testbild ist aber größer und wir wollen es mit der Sliding-Window-Methode verarbeiten. Für unser Beispiel machen wir das Testbild nur ein klein wenig größer: es hat die Größe 16x16x3. Dennoch können wir hier die Sliding-Window-Methode mit Stride 2 anwenden:
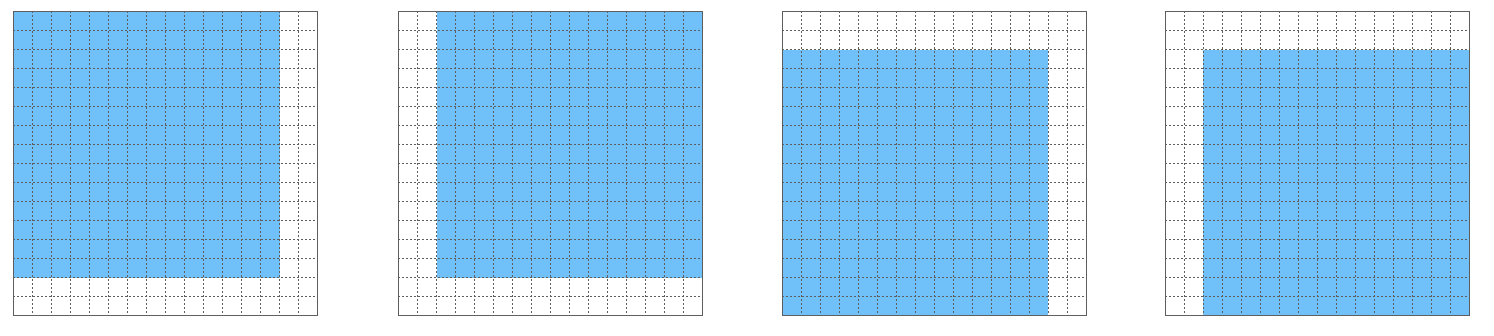
Statt jetzt unser ursprüngliches CNN vier Mal über das Testbild laufen zu lassen, geben wir dem CNN unseren 16x16x3-Input. Die Konvolutionsoperation erlaubt es ohne weiteres, auch ein größeres Bild zu verarbeiten. Der Effekt ist lediglich, dass sich die Größen der Schichten entsprechend ändern. In der folgenden Abbildung sehen wir die angepassten Größen. die ursprüngliche Größe ist blau markiert und sitzt auf der ersten Position des Sliding Window.
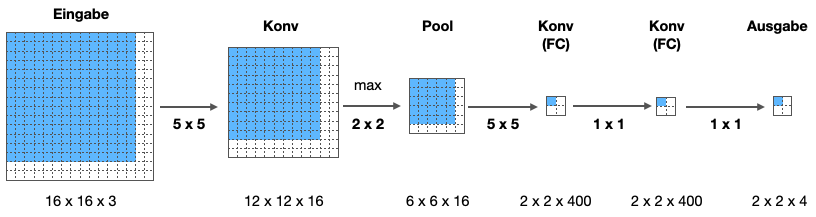
Jetzt ist es so, dass das Ergebnis des (blauen) 14x14-Teilbildes genau dem linken oberen Wert der 2x2-Ausgabematrix entspricht.
Schieben wir das Bild um 2 Pixel nach rechts, sehen wir, dass das Ergebnis dieses (grünen) 14x14-Teilbildes genau dem rechten oberen Wert der 2x2-Ausgabematrix entspricht.
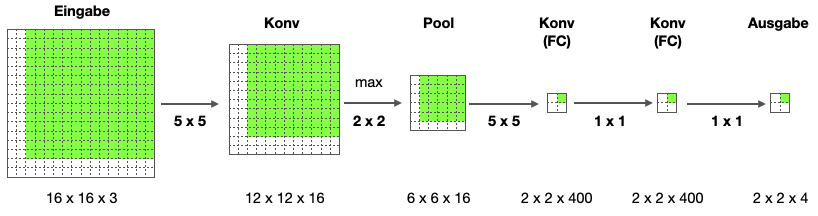
Somit rechnen wir mit diesem vergrößerten Netzwerk gleichzeitig alle vier Sliding-Window-Positionen auf dem 16x16-Bild aus. Das heißt, anstatt vier Mal das ursprüngliche CNN zu durchlaufen, können wir mit dem leicht vergrößerten CNN die äquivalente Berechnung in einem Durchlauf machen. Wir nutzen dabei die vielen Redundanzen aus, die sich in den überlappenden Regionen ergeben.
Wenn wir jetzt ein deutlich größeres Bild vor uns haben, können wir dennoch unser CNN in einem Durchlauf über das Bild laufen lassen und bekommen eine Map, auf der wir für jede Sliding-Window-Position ein Neuron haben, das uns sagt, ob dort ein Objekt erkannt wurde und von welcher Art es ist.
Jetzt sind aber noch mehrere Probleme ungelöst:
- Präzision: Wir bekommen mit obiger Methode keine präzisen Bounding Boxes. Die Objekte können deutlich kleiner als eine Zelle sein oder sich über mehrere Zellen erstrecken.
- Mehrere Objekte: Die Unterscheidung, ob ein Objekt vorliegt oder mehrere, kann hier nicht gezogen werden.
Wir nähern uns diesen Problemen bei der Besprechung des YOLO-Algorithmus.
11.3 YOLO - You Only Look Once
Das YOLO-Verfahren You Only Look Once wurde 2016 vorgestellt und wurde insbesondere aufgrund seiner hohen Verarbeitungsgeschwindigkeit schnell populär (Redmon et al. 2016). YOLO wurde am Allen Institute for AI der University of Washington entwickelt. Eine hohe Geschwindigkeit bei der Objekterkennung ist in vielen Szenarien wichtige Voraussetzung, z.B. im Bereich autonomer Fahrzeuge oder bei Augmented-Reality-Anwendungen.
YOLO erreicht seine Performance durch die Integration mehrerer Mechanismen in ein einziges CNN, das zur Erkennungszeit einen einzigen Durchlauf benötigt, um alle Gitterzellen zu verarbeiten. Daher auch der Name You Only Look Once. Die meisten anderen Verfahren arbeiten hingegen mehrere Gitterzellen oder Regionen nacheinander ab.
Es gibt zwei Weiterentwicklungen vom gleichen Team: YOLOv2 (Redmon and Farhadi 2017) und YOLOv3 (Redmon and Farhadi 2018).
Auf der der Homepage des Erstautoren Joseph Redmon finden Sie weitere Informationen und das Darknet Neural Network Framework (open-source Framework in C und CUDA). Siehe auch Paperswithcode.
11.3.1 Grundmechanismus
Wir hatten ursprünglich unser Bild in ein Gitter unterteilt:
Wir hatten einen Vektor \(y\) der Länge 8 so definiert:
\[ y= \left( \begin{array}{c} p_c \\ b_x \\ b_y \\ b_h \\ b_w \\ c_1 \\ c_2 \\ c_3 \end{array}\right) \]
Jetzt können wir ein CNN erstellen, das dieses Gitter verarbeitet und für jede Gitterzelle einen solchen Vektor ausgibt. In der Ausgabe ist also für jede Zelle der Vektor \(y\) in den Kanälen kodiert.
Wenn hier in der Ausgabe in einer Zelle ein Auto detektiert wird, dann ist dort \(p_c = 1\) und die entsprechenden Angaben für die Bounding Box sind da (die Bounding Box kann auch aus der Zelle herausragen). Wenn wir dieses Netz auf entsprechenden Trainingsdaten trainieren, können wir bei einem Testbild für jede Zelle vorhersagen, ob dort ein Objekt ist, von welchem Typ es ist und wie die Bounding Box aussieht.
Noch ein Hinweis zur Bounding Box: jede Zelle dient hier als eigenes Koordinatensystem mit \((0,0)\) links oben und \((1,1)\) rechts unten. Der Mittelpunkt \((b_x, b_y)\) muss innerhalb dieser Koordinaten liegen. Höhe und Breite sind so skaliert, das die Höhe der Gitterzelle 1 ist für \(b_h\) und die Breite der Gitterzelle 1 für \(b_w\). Höhe und Breite können auch Werte \(>1\) annehmen.
Ein Problem ist natürlich, dass zwei benachbarte Zellen, das selbe Objekt detektieren können, so dass mehr Objekte erkannt werden, als wirklich da sind.
11.3.2 IOU und Non-Max Suppression
Wie stellen wir fest, dass ein und dasselbe Objekt mehrfach “erkannt” wurde? Der wichtigste Indikator ist die Bounding Box bzw. das Überlappen von zwei Bounding Boxes.
Wir definieren zunächst das IOU-Maß für Überlappung und sehen und dann den Non-Max-Suppression-Algorithmus an, der Mehrfach-Erkennungen verhindert bzw. reduziert.
Beides sind Techniken der klassischen Bildverarbeitung.
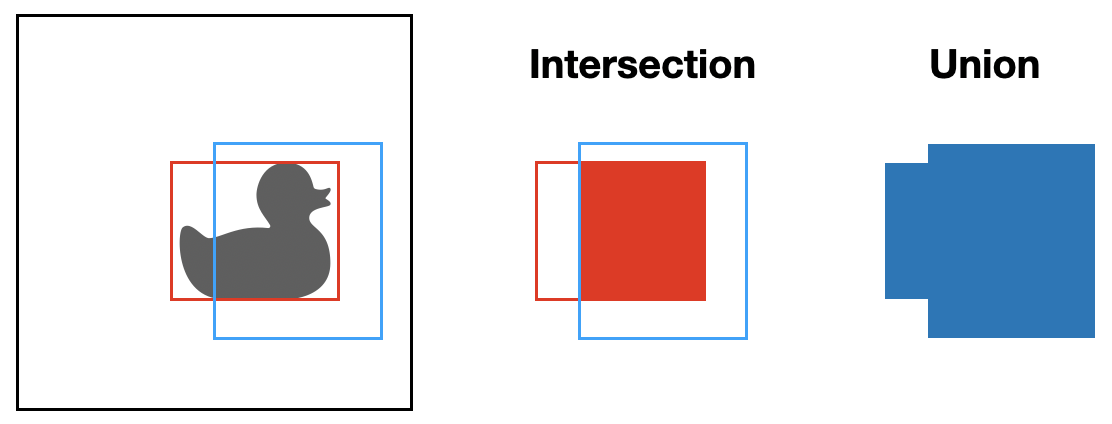
Intersection over Union (IOU)
Wenn wir zwei Bounding Boxes \(B_1\) (rot) und \(B_2\) (blau) haben wie in der Abbildung, dann können wir die Schnittmenge (Intersection) und die Vereinigungsmenge (Union) bilden:
Als Maß für den Überlapp der beiden Boxen definieren wir
\[ \mbox{IOU}(B_1, B_2) = \frac{\mbox{intersection}(B_1, B_2)}{\mbox{union}(B_1, B_2)} = \frac{B_1 \cap B_2}{B_1 \cup B_2} \]
Der Wert ist natürlich kleiner-gleich eins, da die Schnittmenge immer kleiner oder gleich der Vereinigungsmenge ist. Die Extremwerte sind 1 für zwei deckungsgleiche Boxen und 0 für zwei Boxen ohne Überschneidung.
Non-Max Suppression
Für den Non-Max-Suppression-Algorithmus nehmen wir an, dass wir eine Liste mit mehreren Bounding Boxes als Eingabe haben. Jede Bounding Box hat einen Plausibilitätswert \(p_c \in [0,1]\), der angibt, wie verlässlich diese Bounding-Box-Vorhersage ist.
Unser Ziel ist es, eine Teilmenge dieser Liste auszugeben, die zwei Bedingungen erfüllt:
- jede Bounding Box hat eine Mindest-Plausibilität
- keine zwei Bounding Boxes beziehen sich auf dasselbe Objekt
Eigenschaft 2 lässt sich natürlich nur approximativ herstellen. Wir nehmen an, dass Überlappung ein Indikator dafür ist, dass zwei Bounding Boxes sich auf dasselbe Objekt beziehen.
Hier ein Beispiel mit drei Bounding Boxes:
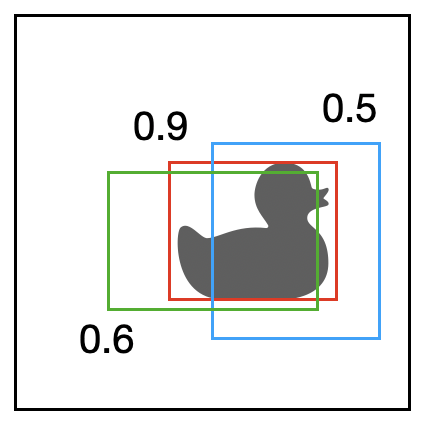
Non-max suppression funktioniert so, dass es sich die Zelle mit dem höchsten \(p_c\) nimmt - wir nennen sie die Max-Zelle - und alle Zellen löscht, die mit der Max-Zelle überlappen (z.B. einen IOU > 0.5 haben). Im obigen Beispiel für die rote Bounding Box gewinnen und die grüne und blaue würden gelöscht werden.
Es kann sein, dass noch weitere Objekte im Bild sind, also wird die Zelle mit dem nächst höchsten Wert zur Max-Zelle und so weiter. Hier würde die obere Ente als nächstes gewählt werden.
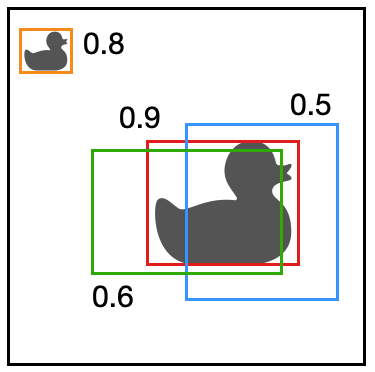
Hier nochmal der Non-Max-Suppression-Algorithmus:
Unsere Bounding Boxes liegen als Vektoren der folgenden Form vor (bei einem 19x19-Gitter wären es die 361 Vektoren jeder Zelle):
\[ \left( \begin{array}{c} p_c \\ b_x \\ b_y \\ b_h \\ b_w \end{array}\right) \]
Wir vereinfachen das Problem, indem wir die Kategorien \(c_1, c_2, \ldots\) weglassen.
Wir erzeugen zwei Listen \(A\) und \(B\) und befüllen \(A\) mit allen Vektoren, bei denen \(p_c > 0.6\) (das heißt, alle Vorhersagen mit \(p_c \leq 0.6\) werden verworfen).
Solange \(A\) nicht leer ist, tun wir Folgendes: * Wähle aus \(A\) den Vektor \(v\) mit dem höchstem \(p_c\) und verschiebe ihn in \(B\) * Lösche alle Vektoren \(w\) aus \(A\), für die gilt \(\mbox{IOU}(v, w) \geq 0.5\)
Am Ende enthält \(B\) alle verbleibenden Bounding-Boxes und \(A\) muss zwangsläufig leer sein.
Wenn wir wieder mehrere Kategorien vorhersagen möchten, durchlaufen wir obigen Algorithmus für jede Kategorie einzeln.
11.3.3 Ankerboxen
Ein Problem ist weiterhin, dass mehrere Objekte sehr dicht oder überlappend im Bild sein können, so dass die Mittelpunkte in der selben Gitterzelle sind. Da eben gezeigte Verfahren kann maximal ein Objekt pro Gitterzelle erkennen.
Ankerboxen (anchor boxes) versuchen das Problem zu lösen, indem man verschiedene Grundformen definiert, und jede Gitterzelle so viele verschiedene Objekte erkennen kann, wie es Grundformen gibt.
Wir wählen als Beispiel zwei Grundformen als Ankerboxen: ein hohes Rechteck (z.B. für einen stehenden Menschen) oder ein eher breites Rechteck (z.B. für ein Auto in Seiten- oder Schrägansicht). Natürlich kann man weitere definieren (verschiedene Ausprägungen von lang/breit oder quadratisch).
Diese zwei Ankerboxen werden gleichzeitig im Outputvektor \(y\) kodiert, indem wir die Information dort einfach zweifach aufführen, einmal für jede Ankerbox. Unser Beispielvektor der Länge 8 wird so zu einem Vektor der Länge 16:
\[ y= \left( \begin{array}{c} p_c \\ b_x \\ b_y \\ b_h \\ b_w \\ c_1 \\ c_2 \\ c_3 \\ p_c \\ b_x \\\vdots \end{array}\right) \]
Die ersten 8 Komponenten stehen also für Ankerbox 1 und die zweiten 8 für Ankerbox 2. In der Abblidung könnte \(y\) für die Zelle in Zeile 3 und Spalte 3 so aussehen:
\[ y= \left( \begin{array}{c} 1 \\ 0.4 \\ 0.2 \\ 2.9 \\ 0.9 \\ 1 \\ 0 \\ 0 \\ 1 \\ 0.5 \\ 0.3 \\ 2.6 \\3.2\\0\\1\\0\end{array}\right) \]
Wir haben also bei einem 19x19-Gitter einen Output der Form 19x19x16. Alternativ können wir auch sagen 19x19x2x8.
Der Algorithmus von oben wird dahingehend modifiziert, dass nur gleiche Ankerboxen konkurrieren.
11.3.4 Gesamtsystem
Jetzt fügen wir alles zusammen. Wir nehmen ein 3x3-Gitter und drei Kategorien: Mensch, Auto, Motorrad. Wir verwenden zwei Ankerboxen (wie oben). Dann hat unser Output die Form 3x3x16. Hier sehen wir das Bild mit 3x3-Gitter:
Für alle Zellen außer der mit dem Auto bekommen wir Vektoren dieser Art. Die Punkte bedeuten “irgendein Wert”:
\[ \left( \begin{array}{c} 0 \\ \ldots \\ \ldots \\ \ldots \\ \ldots \\ \ldots \\ \ldots \\ \ldots \\ 0 \\ \ldots \\ \ldots \\ \ldots \\\ldots\\\ldots\\\ldots\\\ldots\end{array}\right) \]
Die Zelle mit dem Auto sollte folgenden Output haben. Man beachte die 1 bei \(p_c\), die vier Werte für die rote Bounding Box und die 1 bei \(c_2\):
\[ \left( \begin{array}{c} 0 \\ \ldots \\ \ldots \\ \ldots \\ \ldots \\ \ldots \\ \ldots \\ \ldots \\ 1 \\ 0.4 \\ 0.3 \\ 0.7 \\ 0.7 \\ 0 \\1\\0\end{array}\right) \]
Wir schauen uns ein zweites Beispiel an (ebenfalls aus [Ng CNN]). Wir haben wieder unser 3x3-Gitter, aber diesmal zwei Objekte:
Da wir zwei Ankerboxen haben, bekommen wir für jede der 3x3 Zellen 2 Bounding Boxes, also 18 Bounding Boxes (Bild 1).
Unser Non-Max-Suppression-Algorithmus sortiert alle Bounding Boxes mit \(p_c \leq 0.6\) aus (Bild 2) und bestimmt dann für jede Klasse separat, welche Bounding Box verwendet werden soll (Bild 3).
YOLO ist aktuell einer der populärsten und schnellsten Algorithmen zur Objekterkennung.
11.4 R-CNN
Diese Methoden werden hier nur grob skizziert.
Ein Nachteil der Sliding-Windows-Methoden, die wir uns angesehen haben, ist, dass viele Zellen untersucht werden, die “offensichtlich” nichts von Interesse enthalten.
Die Methode R-CNN (für: “Regions with CNN features”) schlägt vor, in einem ersten Schritt mit klassischen Methoden der Bildverarbeitung wie blob detection und image segmentation die “interessanten” Regionen zu identifizieren und nur auf diesen Regionen mit einem CNN Untersuchungen laufen zu lassen (Girshick et al. 2014). Diesen Schritt nennt man Region Proposal.
Hier sehen wir das Ergebnis von “Blob Detection”, das anschließend für eine Segementierung verwendet werden kann, wo man “Blobs” auswählt, die eine relevante Form haben (ähnlich zu den Anchorboxen), um dann auf diese Regionen das CNN anzusetzen.
Das Paper von Girshick et al. (2014) schließt mit diesen schönen Worten ab:
We conclude by noting that it is significant that we achieved these results by using a combination of classical tools from computer vision and deep learning (bottom- up region proposals and convolutional neural networks). Rather than opposing lines of scientific inquiry, the two are natural and inevitable partners.
R-CNN war relativ langsam, weil jede Region nacheinander durch ein CNN bearbeitet wurde. In dem Follow-Up-Paper Fast R-CNN werden durch Konvolution alle Regionen gleichzeitig von einem CNN verarbeitet, ähnlich wie in “Sliding Window als Konvolution” dargestellt (Girshick 2015).
In einem weiteren Follow-Up-Paper Faster R-CNN wurden die klassischen Methoden, um die interessanten Regionen zu finden durch ein eigenes CNN für das region proposal ersetzt, was wiederum zu einer erheblichen Beschleunigung führte (Ren et al. 2017).