import tensorflow
import matplotlib.pyplot as plt
import numpy as np
import time
import math9 Optimierung und Datensätze
In diesem Kapitel gehen wir auf Methoden ein, die während der Optimierung besser durch die Fehlerlandschaft navigieren, um so z.B. lokale Minima zu vermeiden. Das Schlüsselkonzept heißt Momentum, weil weitere Methoden darauf aufbauen. Außerdem lernen wir drei Datensätze in Keras kennen: FashionMNIST, CIFAR-10 und CIFAR-100.
Momentum, RMSprop, Adagrad, Adadelta, Adam, Nadam
Nach Abschluss dieses Kapitels können Sie
- das Konzept Momentum motivieren und erklären
- noch weitere Optimierungsmethoden außer Momentum benennen und erklären
- Optimierungsmethoden in Keras auswählen und anwenden
- mit den Datensätzen FashionMNIST, CIFAR-10 und CIFAR-100 in Keras umgehen
Datensätze
| Name | Daten | Anz. Klassen | Klassen | Trainings-/Testdaten | Ort |
|---|---|---|---|---|---|
| FashionMNIST | s/w-Bilder (28x28) | 10 | z.B. T-Shirt, Trouser, Dress, Sneaker | 60000/10000 | 9.3.1 |
| CIFAR-10 | Farbbilder (32x32) | 10 | z.B. Flugzeug, Auto, Katze, Hund | 50000/10000 | 9.3.2 |
| CIFAR-100 | Farbbilder (32x32) | 100 | z.B. Bieber, Delphin, Apfel, Orange | 50000/10000 | 9.3.3 |
Importe
9.1 Optimierungsmethoden
Wie bereits erwähnt ist die Lernrate \(\alpha\) ein relativ grober Mechanismus, um den Gradientenabstieg zu steuern. Man kann ich vorstellen, dass man \(\alpha\) eigentlich dynamisch während des Trainings anpassen müsste. Man könnte sich ferner überlegen, dass die vielen Gewichte mit individuellen Lernraten behandelt werden müssten. Genau darum geht es bei den folgenden Verfahren, die in Keras schlicht als optimizer bezeichnet werden.
Wir erinnern uns an den Updateschritt der Parameter. Wir berechnen zunächst ein Delta, das sich aus dem negativen Gradienten ergibt:
\[ \Delta w^{[t]} := - \frac{\partial J}{\partial w^{[t]}} \]
Wir benutzen Index \(t\), um einen Schritt bzw. Zeitpunkt zu kennzeichnen.
Mit Hilfe des Deltas und der Lernrate \(\alpha\) führen wir das Update der Gewichte durch:
\[ w^{[t+1]} := w^{[t]} + \alpha \Delta w^{[t]} \]
Wir sehen uns zunächst die Methoden theoretisch an und vergleichen sie später in Keras.
Zwei schöne Quellen: Der exzellente Übersichtsartikel An overview of gradient descent optimization algorithms von Ruder (2016) und das Video Deep Learning: Loss and Optimization - Part 3 von Andreas Maier (FAU Erlangen).
9.1.1 Momentum
Ein Problem beim Gradientenabstieg ist, dass das Verfahren an bestimmten Stellen - sogenannten ravines (Schluchten) - der Fehlerlandschaft in oszillierende Bewegungen verfallen und nur langsamen Fortschritt erzielen. In Abbildung 9.1 sehen wir zwei Gewichte im Koordinatensystem. Die dritte Achse (auf den Betrachter zulaufend) stellt den Fehler dar (diese Achse wird durch die Höhenlinien und Schattierung angezeigt). Die zackige Linie zeigt den Weg der zwei Gewichte beim Grandientenabstieg. Das nennt man “Oszillieren” und führt hier sogar dazu, dass das Optimum (i.d.R. das Minimum) nicht erreicht wird.
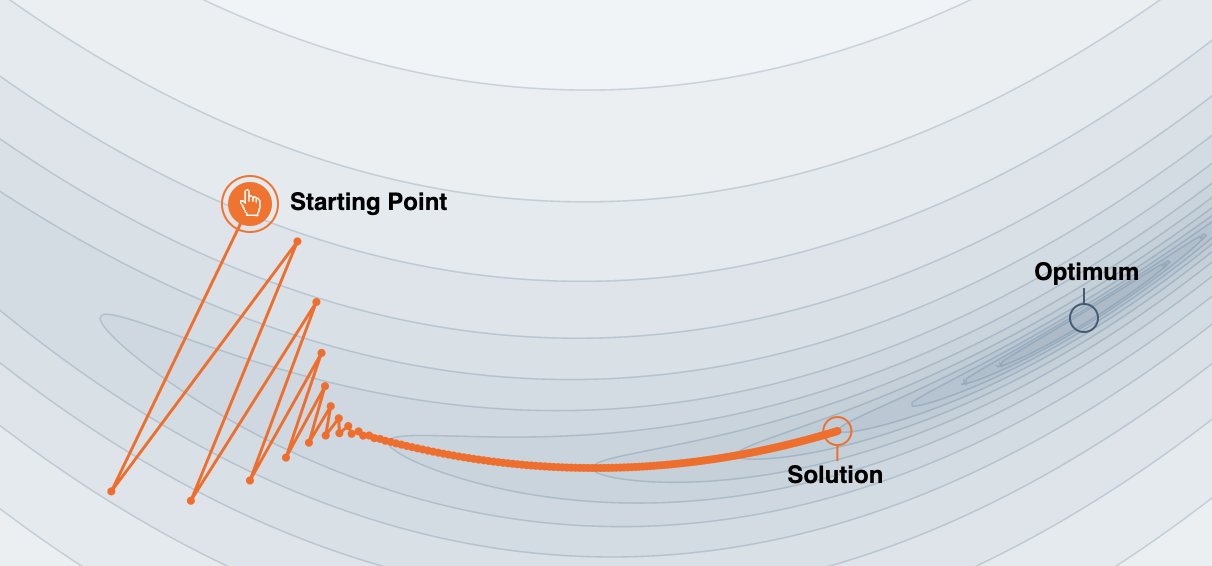
In der nächsten Abbildung sehen wir zwei Schritte auf dem Weg zum Minimum genauer an. Man sieht, dass die w1-Komponente beide Male in die “richtige” Richtung weist, wohingegen dei w2-Komponente in unterschiedliche Richtungen deutet (mathematisch: unterschiedliche Vorzeichen). Wenn bei den nächsten Schritten die w2-Komponente immer wieder so vorkommt, läuft man quasi “im zick-zack” und daher sehr langsam auf das Minimum zu.
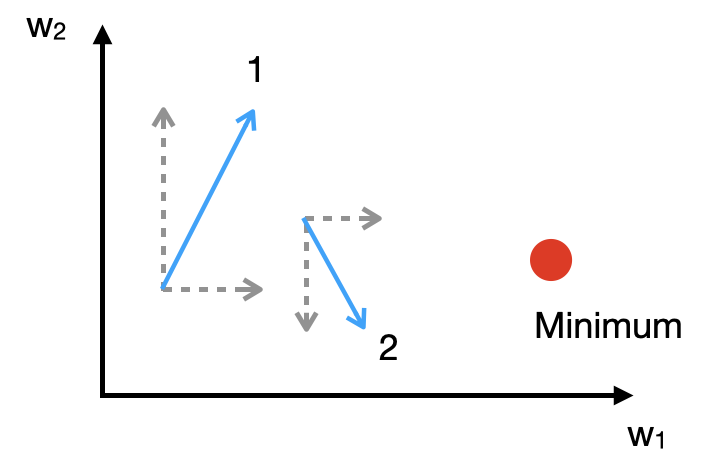
Nun kann man den Updates einen “Schwung” (engl. momentum) mitzugeben, indem ein Anteil des vorherigen Update-Schritts mitaddiert wird (Rumelhart, Hinton, and Williams 1986; Qian 1999; Sutskever et al. 2013; Ruder 2016). In der Abbildung kann man das so verstehen: Wenn die Schritte 1 und 2 im nächsten Schritt berücksichtigt werden, hat die w1-Komponente einen deutlich größeren Einfluss, da die w2-Komponenten unterschiedliche Vorzeichen haben und daher subtrahiert werden. Momentum wurde bereits 1986 von Rumelhart, Hinton und Williams (1986) in ihrem Meilenstein-Paper zu Backpropagation in dieser Form vorgeschlagen. Die Autoren schlagen dort Momentum als ein Tool vor, das es erlaubt, die Lernrate zu erhöhen, ohne dass dies zu Oszillation führt.
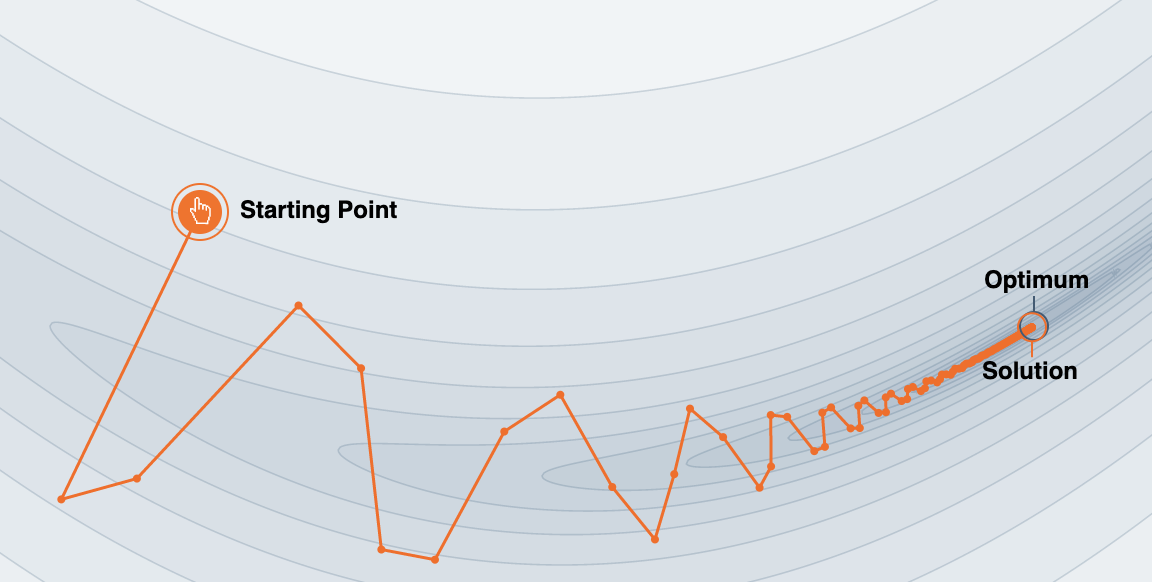
Hier sehen Sie in Abblidung 9.2 was passiert, wenn man ein Momentum der Stärke \(\beta = 0.8\) einstellt.
Beim Verfahren Momentum führen wir bei der Berechnung von \(\Delta w\) einen Term \(s_w\) ein (\(s\) wie smoothed), über den wir den Gradienten modifizieren können.
\[\Delta w^{[t]} := - s_w^{[t]} \]
Das \(s_w\) repräsentiert den Gradienten \(\frac{\partial J}{\partial w}\), der aber mit dem Gradienten des vorigen Zeitschritts \(t-1\) linearkombiniert wird, sozusagen eine “Glättung”, wobei \(\beta \in [0, 1]\):
\[s_w^{[t]} := \beta\, s_w^{[t-1]} + (1 - \beta)\, \frac{\partial J}{\partial w^{[t]}}\]
Gesteuert wird die Trägheit durch einen Faktor \(\beta\). Je höher \(\beta\), um so stärker die Trägheit, d.h. der aktuelle Gradient geht weniger stark in die Berechnung des Updates ein. Der Faktor \(\beta\) wird in der Regel relativ hoch gewählt, z.B. \(0.9\).
Diese Methode führt also dazu, dass eine Bewegung in die selbe Richtung mit der Zeit an Fahrt gewinnt. Nur wenn sich die Richtung ändert, verliert sich auch der Schwung.
In der Signalverarbeitung wird diese Art der “Glättung” eines Originalsignals auch exponential moving average oder exponential smoothing genannt. Das “exponential” bezieht sich darauf, dass vergangene Signale exponentiell verringert in den aktuellen Wert eingehen.
Wir probieren das anhand der Abbildung nachzurechnen.

Für Zeitschritt \(t=1\) könnten die beiden Komponenten folgende Werte haben:
\[ \begin{align*} \frac{\partial J}{\partial w_1^{[1]}} &= 3\\[2mm] \frac{\partial J}{\partial w_2^{[1]}} &= 6 \end{align*} \]
Für Zeitschritt \(t=2\) dann die folgenden Werte:
\[ \begin{align*} \frac{\partial J}{\partial w_1^{[2]}} &= 2\\[2mm] \frac{\partial J}{\partial w_2^{[2]}} &= -4 \end{align*} \]
Komponente \(w_1\)
Jetzt sehen wir uns die Entwicklung von \(s_{w_1}^{[t]}\) an. Beim null-ten Zeitschritt ist \(s_{w_1}^{[0]}=0\):
\[ \begin{align*} s_{w_1}^{[1]} &:= 0.9 \cdot s_{w_1}^{[0]} + 0.1 \cdot \frac{\partial J}{\partial w_1^{[1]}} = 0.1 \cdot 3 = 0.3\\[2mm] s_{w_1}^{[2]} &:= 0.9 \cdot s_{w_1}^{[1]} + 0.1 \cdot \frac{\partial J}{\partial w_1^{[2]}} = 0.9 \cdot 0.3 + 0.1 \cdot 2 = 0.47 \end{align*} \]
Komponente \(w_2\)
Analog für die zweite Komponente \(s_{w_2}^{[t]}\). Auch hier ist \(s_{w_2}^{[0]}=0\):
\[ \begin{align*} s_{w_2}^{[1]} &:= 0.9 \cdot s_{w_2}^{[0]} + 0.1 \cdot \frac{\partial J}{\partial w_2^{[1]}} = 0.1 \cdot 6 = 0.6\\[2mm] s_{w_2}^{[2]} &:= 0.9 \cdot s_{w_2}^{[1]} + 0.1 \cdot \frac{\partial J}{\partial w_2^{[2]}} = 0.9 \cdot 0.6 + 0.1 \cdot (-4) = 0.14 \end{align*} \]
Was man hier beachten sollte ist, dass die “oszillierende” Komponente \(w_2\) nicht zwischen Extremen hin und her schwankt, sondern nur verlangsamt wird. Komponente \(w_1\) schwankt nicht und gewinnt somit zusehend “an Fahrt”.
Weitere Erklärungen von Momentum
Andrew Ng hat dazu ein schönes Erklärvideo: Gradient Descent With Momentum.
Die Abbildungen oben wurden mit einer interaktiven Visualisierung auf der Webseite Why Momentum Really Works von Gabriel Goh (2017) angefertigt. Dort finden Sie auch weitere Erklärungen zur Momentum-Methode.
Einsatz
Bekannte Netze, die Momentum nutzen:
- AlexNet: \(\beta = 0.9\) (Krizhevsky, Sutskever, and Hinton 2012)
- ResNet: \(\beta = 0.9\) (He et al. 2016)
9.1.2 Weitere Verfahren
Adagrad
Adagrad steht für Adaptive Gradient (Duchi, Hazan, and Singer 2011). Ein Grund, warum eine Lernrate \(\alpha\) suboptimal sein könnte, ist, dass alle Parameter \(w_i\) gleich behandelt werden, dabei könnte es sein, dass wir für Parameter \(w_3\) in kleineren Schritten gehen sollten als für \(w_5\). Adagrad individualisiert die Lernrate nach Parametern. Das Prinzip dabei lautet: je häufiger ein Parameter schon geupdatet wurde, umso kleiner das nächste Update.
Schauen wir uns das Delta für jedes Einzelgewicht \(w_i\) an:
\[ \Delta w_i^{[t]} := - \alpha \nabla J(w_i^{[t]}) \]
Adagrad reduziert das \(\alpha\) basierend auf der Häufigkeit vergangener Updates von \(w_i\):
\[ \Delta w_i^{[t]} := - \frac{\alpha}{\sqrt{G_{[t], ii} + \epsilon}} \nabla J(w_i^{[t]}) \]
Dabei ist \(G_t\) eine Matrix, die auf der Diagonalen die Summe der Quadrate aller bisherigen Gradienten nach jeweils \(w_i\) enthält. Das \(\epsilon\) soll verhindern, dass durch Null dividiert wird und ist sehr klein (z.B. \(10^{-8}\)). Laut Ruder (2016) performt das Verfahren deutlich schlechter, wenn man die Wurzel weglässt.
Der Vorteil der Methode ist die automatische Anpassung der Lernrate. Der Nachteil ist, dass die Lernrate im Verlauf des Lernens auf praktisch Null sinkt und somit kein Lernen mehr stattfindet.
Adadelta und RMSprop
Die Verfahren Adadelta behebt den Nachteil von Adagrad, indem nicht alle vergangenen Gradientenwerte addiert, sondern nur eine begrenzte Historie betrachtet, wo ältere Werte über die Zeit immer geringeren Einfluss haben (Zeiler 2012).
Statt der Matrix \(G\) verwenden wir als Speicher \(E\), wo die Quadrate der Gradienten immer aufsummiert werden, wobei die alten Werte über die Zeit verblassen.
\[ E_i^{[t]} = \gamma E_i^{[t-1]} + (1-\gamma) \nabla J(w_i^{[t]})\]
Bei der Berechnung des Delta verwenden wir wie bei Adagrad das \(E\) im Nenner, um die Gewichtsänderung zu dämpfen:
\[ \Delta w_i^{[t]} := - \frac{\alpha}{\sqrt{E_i^{[t]} + \epsilon}} \nabla J(w_i^{[t]}) \]
Für weitere Details verweisen wir auf den Artikel von Ruder (2016).
RMSprop steht für Root Mean Square Propagation und ist eine sehr ähnliche, parallel entwickelte, Methode. Sie wurde nicht publiziert, sondern lediglich von Geoffrey Hinton in einer Vorlesung vorgestellt. Sie können sich die Folien der Vorlesung anschauen (ab Folie 26).
Siehe auch RMSProp (Andrew Ng)
Einsatz
Bekannte Netze, die RMSProp nutzen:
- LSTM bei Graves (2014)
Adam
Adam gehört zu den populärsten Optimierungsmethoden und steht für Adaptive Moment Estimation (Kingma and Ba 2015). Auch dieses Verfahren berechnet die adaptive Lernrate für jeden Parameter. Im Unterschied zu Adagrad wird hier zusätzlich noch Momentum verwendet und auch das Momentum wird anhand früherer Anpassungen modifiziert.
Siehe auch Adam Optimization Algorithm (Andrew Ng)
Einsatz
Bekannte Netze, die Adam nutzen:
- Transformer (Vaswani et al. 2017)
- BERT (Devlin et al. 2018)
Nesterov accelerated gradient (NAG)
Eine Variante von Momentum ist Nesterov accelerated gradient (NAG). Hier sei nur auf den ausführlichen Online-Artikel Nesterov Accelerated Gradient and Momentum von James Melville (2016) hingewiesen (ansonsten siehe das russische Originalpaper Nesterov 1983).
Nadam
Nadam steht für Nesterov-accelerated Adaptive Moment Estimation und kombiniert Adam und NAG (Dozat 2016).
9.1.3 Welche Methode nutzen?
Ruder (2016) empfiehlt Adam als derzeit bestes Gesamtpaket, betont aber, dass viele Methoden eine ähnlich gute Performance haben. In einem Vergleich, den wir zum Ende des Kapitels anstellen, schneiden Adam, RMSprop und Nadam am besten ab. Die Performance hängt aber sicherlich auch von der Problemstellung, also den Daten, ab.
9.2 Optimierungsmethoden in Keras
EPOCHS = 20
LEARNING_RATE= 0.19.2.1 Daten
Wir nehmen wieder den Datensatz MNIST, bei dem es um die Erkennung von handgeschriebenen Ziffern (0..9) geht.
Daten einlesen
from tensorflow.keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
print('x_train: ', x_train.shape)
print('y_train: ', y_train.shape)
print('x_test: ', x_test.shape)
print('y_test: ', y_test.shape)x_train: (60000, 28, 28)
y_train: (60000,)
x_test: (10000, 28, 28)
y_test: (10000,)Daten vorverarbeiten
Wir linearisieren die Daten zu Vektoren der Länge 784 (= 28*28) und normalisieren wir die Pixelwerte (0..255) auf das Interval [0, 1].
x_train = x_train.reshape(60000, 784)/255.0
x_test = x_test.reshape(10000, 784)/255.0One-Hot Encoding
Wir benutzen One-Hot Encoding, d.h. jede Ziffer wird durch einen Vektor der Länge 10 repräsentiert.
from tensorflow.keras.utils import to_categorical
y_train_1hot = to_categorical(y_train, 10)
y_test_1hot = to_categorical(y_test, 10)
print("y_train: ", y_train_1hot.shape)
print("y_test: ", y_test_1hot.shape)y_train: (60000, 10)
y_test: (10000, 10)9.2.2 Vergleich der Optimierungsmethoden
Wir haben im Theorieteil verschiedene Optimierungsmethoden kennen gelernt. Wir vergleichen jetzt das gleiche Netz mit den gleichen Daten, aber unterschiedlichen Optimierungsmethoden.
Hyperparameter
Hyperparameter sind Parameter, die sich während des Trainings nicht verändern. Das können ganz verschiedene Aspekte eines Netzwerks sein:
- die Anzahl der Schichten und Neuronen
- das Optimierungsverfahren (SGD, Adagrad oder Adam)
- die Anzahl der Epochen
- die Lernrate \(\alpha\) (falls diese im Training fix ist)
Wenn wir aber fünf verschiedene Netze \(N_1, \ldots, N_5\) mit verschiedenen Hyperparametern trainieren, wie vergleichen wir sie? Wir könnten die Testdaten nehmen. Aber wenn wir uns aufgrund der Testdaten-Performance für Netz \(N_3\) entscheiden, womit berechnen wir dann die endgültige Performance auf einem “neutralen” (d.h. ungesehenen) Datensatz?
Um dies zu umgehen, nimmt man aus den Trainingsdaten einen Satz Validierungsdaten. Man vergleicht die Netze \(N_1, \ldots, N_5\) auf den Validierungsdaten und berechnet die finale Performance mit dem Gewinnernetzwerk auf den Testdaten.
Optimierungsmethoden in Keras
In TensorFlow/Keras wird die Optimierungsmethode durch ein parametrisierbares Optimizer-Objekt bestimmt, zu finden im Paket tensorflow.keras.optimizers. Wir haben das oben mit SGD gesehen. Dieses Objekt wird dann der Methode compile übergeben. Will man die Standardeinstellungen haben, kann man compile auch einen einfachen String übergeben wie ‘SGD’ oder ‘Adam’.
Es gibt folgende Optimizer-Klassen zur Auswahl:
- SGD: Stochastic Gradient Descent in den folgenden Varianten
- Momentum kann mit Parameter momentum (Wert zwischen 0 und 1, entspricht \(\beta\)) gesteuert werden
- NAG: mit Parameter nesterov (True|False) aktiviert man Nesterov Accelerated Gradient
- Adagrad
- Adadelta
- RMSprop
- Adam
- Nadam
In der Dokumentation unter https://keras.io/optimizers findet man für jeden Optimizer die entsprechenden Parameter.
Experiment
Wir möchten diese Verfahren mit Hilfe mehrerer Netzwerke, die sich nur in der Optimierungsmethode unterscheiden, miteinander vergleichen. Dazu müssen wir einen Teil der Trainingsdaten (10%) als Validierungsdaten entnehmen. Diese Validierungsdaten nehmen wir, um uns für eine Optimierungsmethode zu entscheiden und messen dann damit die Performance auf den Testdaten.
Globale Parameter
Wir definieren für unser “Experiment” ein paar globale Parameter, damit wir leicht Änderungen vornehmen könnten.
EPOCHS = 30
hidden_neurons = 50
# Bezeichner der Optimierungsverfahren
optimizers = ['SGD', 'Adagrad', 'Adadelta', 'RMSprop', 'Adam', 'Nadam']Die Ergebnisse speichern wir in einem Array. Wie die Einträge strukturiert sind, sehen wir gleich.
results = []Modell
Da wir viele Netzwerke erstellen, schreiben wir uns eine Funktion, die ein Netz erstellt, trainiert und evaluiert. Es wird ein assoziatives Array erzeugt, dass alle wichtigen Informationen zu dem Netz-Testlauf enhälte: Titel, Trainingshistorie und Evaluation auf den Testdaten.
Sie sehen hier den Paramter validation_split. Hier kann man einen Prozentsatz (als Zahl zwischen 0 und 1) angeben, den man als Validierungsdaten vorhalten möchte.
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
def processFNN(optimizer):
print(f'\n+++++++++++ {optimizer} ++++++++++')
fnn_data = {} # Daten speichern
fnn_data['title'] = optimizer
model = Sequential()
model.add(Dense(hidden_neurons,
input_shape=(784,),
activation='sigmoid'))
model.add(Dense(10, activation='softmax'))
model.compile(optimizer=optimizer,
loss='categorical_crossentropy',
metrics=['acc'])
# Training
start_time = time.time()
history = model.fit(x_train, y_train_1hot,
epochs=EPOCHS,
verbose=0,
validation_split=0.1)
fnn_data['history'] = history
# Performance auf Testdaten
test = model.evaluate(x_test, y_test_1hot)
fnn_data['test'] = test
duration = time.time() - start_time
print(f'Dauer {duration:.2f} Sek | {EPOCHS} Epochen | Acc Val {test[1]:.3f}')
return fnn_dataTrainingsdurchläufe
Wir durchlaufen alle Optimierungsmethoden in unserem Array und erzeugen einen Testlauf, dessen Ergebnis wir in unseren Ergebnisarray packen.
for op in optimizers:
results.append(processFNN(op))
+++++++++++ SGD ++++++++++2023-04-17 23:01:08.701691: I tensorflow/core/platform/cpu_feature_guard.cc:193] This TensorFlow binary is optimized with oneAPI Deep Neural Network Library (oneDNN) to use the following CPU instructions in performance-critical operations: SSE4.1 SSE4.2
To enable them in other operations, rebuild TensorFlow with the appropriate compiler flags.313/313 [==============================] - 0s 575us/step - loss: 0.2302 - acc: 0.9349
Dauer 35.59 Sek | 30 Epochen | Acc Val 0.935
+++++++++++ Adagrad ++++++++++
313/313 [==============================] - 0s 565us/step - loss: 0.6074 - acc: 0.8769
Dauer 39.45 Sek | 30 Epochen | Acc Val 0.877
+++++++++++ Adadelta ++++++++++
313/313 [==============================] - 0s 607us/step - loss: 1.5106 - acc: 0.7737
Dauer 42.84 Sek | 30 Epochen | Acc Val 0.774
+++++++++++ RMSprop ++++++++++
313/313 [==============================] - 0s 584us/step - loss: 0.1112 - acc: 0.9695
Dauer 39.26 Sek | 30 Epochen | Acc Val 0.970
+++++++++++ Adam ++++++++++
313/313 [==============================] - 0s 573us/step - loss: 0.1069 - acc: 0.9705
Dauer 42.77 Sek | 30 Epochen | Acc Val 0.970
+++++++++++ Nadam ++++++++++
313/313 [==============================] - 0s 570us/step - loss: 0.1129 - acc: 0.9694
Dauer 41.86 Sek | 30 Epochen | Acc Val 0.969Evaluation
Hier sehen wir uns die Entwicklung der Accuracy im Training an: einmal für die Trainingsdaten, einmal für die Validierungsdaten.
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12, 5))
for res in results:
ep = range(1, len(res['history'].history['acc'])+1 )
ax[0].plot(ep, res['history'].history['acc'], label=res['title'])
ax[0].set_ylabel('Acc')
ax[0].set_xlabel('Epochen')
ax[0].legend()
ax[0].set_title('Accuracy Training')
ax[0].grid()
ax[1].plot(ep, res['history'].history['val_acc'], label=res['title'])
ax[1].set_ylabel('Val Acc')
ax[1].set_xlabel('Epochen')
ax[1].grid()
ax[1].set_title('Accuracy Validation')
ax[1].legend()
plt.show()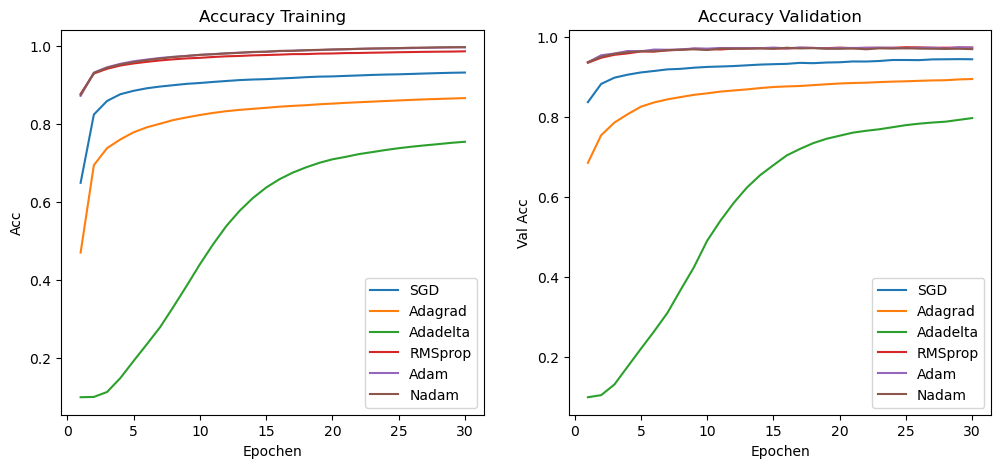
Da man oben wenig erkennen kann, sehen wir uns die Einzelverläufe an:
fig, ax = plt.subplots(nrows=math.ceil(len(results)/2), ncols=2, figsize=(12, 12))
ax = ax.flatten()
i = 0
for res in results:
ep = range(1, len(res['history'].history['acc'])+1 )
ax[i].set(ylim=(0.5, 1))
ax[i].plot(ep, res['history'].history['acc'], 'b', label='Acc')
ax[i].plot(ep, res['history'].history['val_acc'], 'r', label='Val Acc')
ax[i].set_ylabel('Acc')
ax[i].legend()
ax[i].set_title(res['title'])
i += 1
plt.show()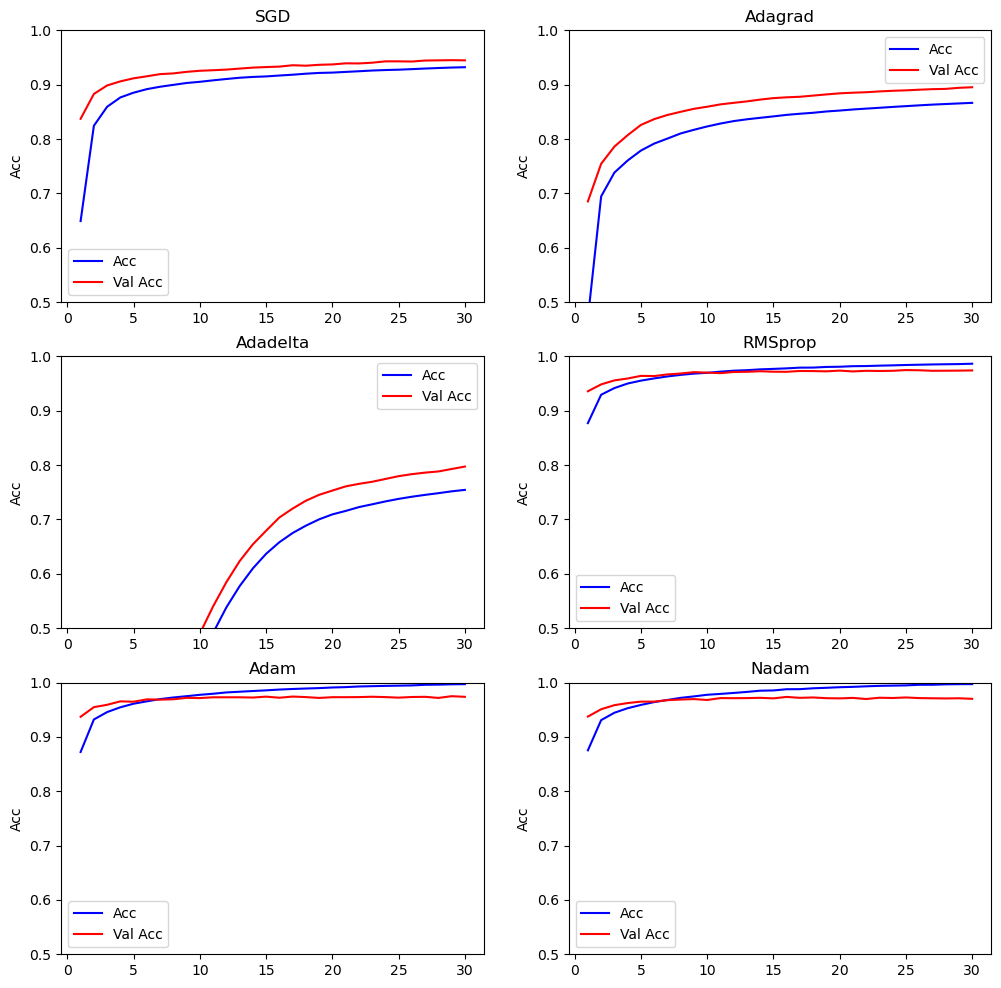
for res in results:
print("{:10} training acc={:.4f} val acc={:.4f} test acc={:.4f}".
format(str(res['title']),
res['history'].history['acc'][EPOCHS-1],
res['history'].history['val_acc'][EPOCHS-1],
res['test'][1]))SGD training acc=0.9320 val acc=0.9447 test acc=0.9349
Adagrad training acc=0.8665 val acc=0.8952 test acc=0.8769
Adadelta training acc=0.7544 val acc=0.7973 test acc=0.7737
RMSprop training acc=0.9865 val acc=0.9742 test acc=0.9695
Adam training acc=0.9970 val acc=0.9737 test acc=0.9705
Nadam training acc=0.9970 val acc=0.9700 test acc=0.9694Auf den Validierungsdaten liegen RMSprop, Adam und Nadam klar vorn. Genau genommen hat Adam gewonnen, so dass man mit Adam auch auf den Testdaten evaluieren müsste. Das heißt, wir erzielen hier 97,4% Accuracy auf den Testdaten mit Adam.
9.3 Datensätze FashionMNIST, CIFAR-10 und CIFAR-100
Wir stellen hier drei Datensätze vor, die fest in Keras eingebaut sind, d.h. Sie können Sie mit einer Zeile Code in Variablen laden. Der Datensatz MNIST ist mittlerweile kaum noch brauchbar, weil er zu leicht ist. Die drei Datensätze - FahsionMNIST, CIFAR-10 und CIFAR-100 - haben steigenden Schwierigkeitsgrad. Insbesondere mit CIFAR-100 kann man schon komplexe Netze (i.d.R. Konvolutionsnetze) testen.
9.3.1 FashionMNIST
Im FashionMNIST-Datensatz geht es darum, Bilder von Kleidungsstücken zu klassifizieren. Es gibt zehn Klassen, die es vorherzusagen gilt, z.B. Pullover, Coat oder Sneaker. Die Bilder haben die Auflösung 28x28 und liegen in Graustufen vor. Der Datensatz enthält 60000 Trainingsbeispiele und 10000 Testbeispiele.
FashionMNIST ist ein Datensatz für die Bilderkennung, der - in Anlehnung an MNIST - eher für Test- oder Lernzwecke geeignet ist. Der Datensatz stammt von der Firma Zalando.
Die 10 Klassen sind wie folgt kodiert:
- 0 = T-shirt/top
- 1 = Trouser
- 2 = Pullover
- 3 = Dress
- 4 = Coat
- 5 = Sandal
- 6 = Shirt
- 7 = Sneaker
- 8 = Bag
- 9 = Ankle boot
from tensorflow.keras.datasets import fashion_mnist
(x_train, y_train), (x_test, y_test) = fashion_mnist.load_data()
print('x_train: ', x_train.shape)
print('y_train: ', y_train.shape)
print('x_test: ', x_test.shape)
print('y_test: ', y_test.shape)x_train: (60000, 28, 28)
y_train: (60000,)
x_test: (10000, 28, 28)
y_test: (10000,)Hier drei Beispiele mit den jeweiligen Klassen:
print('Klasse ', y_train[0])
plt.imshow(x_train[0], cmap='gray')Klasse 9<matplotlib.image.AxesImage at 0x7fb5d9defac0>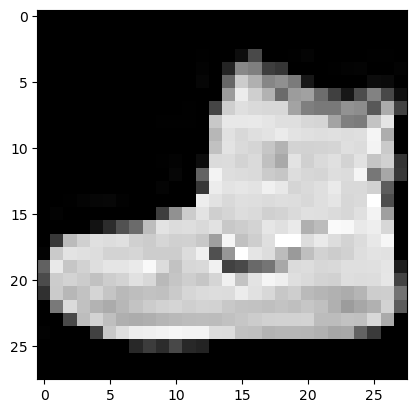
print('Klasse ', y_train[1])
plt.imshow(x_train[1], cmap='gray')Klasse 0<matplotlib.image.AxesImage at 0x7fb5e85f0220>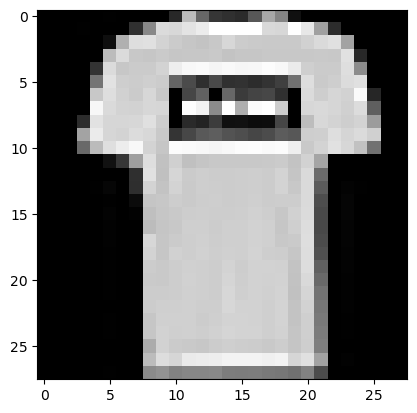
print('Klasse ', y_train[9])
plt.imshow(x_train[9], cmap='gray')Klasse 5<matplotlib.image.AxesImage at 0x7fb5c818ffd0>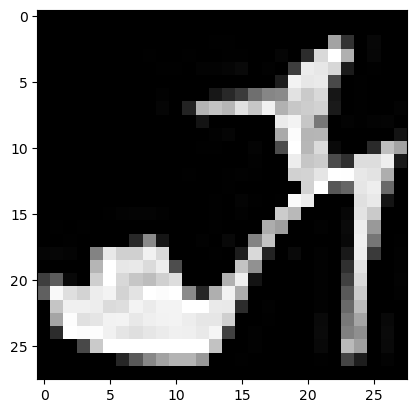
9.3.2 CIFAR-10
Im CIFAR-10-Datensatz geht es darum, Farbbilder von Objekten zu klassifizieren. Es gibt zehn Klassen, die es vorherzusagen gilt, z.B. Airplane, Bird, Dog oder Ship. Die Bilder haben die Auflösung 32x32 und liegen in Farbe vor. Der Datensatz enthält 50000 Trainingsbeispiele und 10000 Testbeispiele.
Der Datensatz CIFAR-10 enthält Farbbilder aus 10 Klassen. CIFAR steht für Canadian Institute For Advanced Research. Den Datensatz erstellt haben Alex Krizhevsky, Vinod Nair und Geoffrey Hinton. Krizhevsky und Hinton sind Ko-Autoren des berühmten AlexNet-Papers von 2012 (Krizhevsky, Sutskever, and Hinton 2012).
Der Datensatz CIFAR-10 besteht aus 60000 32x32-Farbbildern aus 10 Klassen (airplanes, cars, birds, cats, deer, dogs, frogs, horses, ships, trucks). Die Beispiele sind gleichmäßig über die Klassen verteilt, d.h. es gibt 6000 Beispiele pro Klasse. Im Vergleich zu MNIST haben wir also die gleiche Anzahl von Klassen und Daten, aber 3 Farbkanäle, eine geringfügig höhere Auflösung und komplexere Objekte. Das heißt, wir erwarten niedrigere Erkennungsraten im Vergleich zu MNIST.
Die ursprüngliche Quelle ist eine Webseite von Alex Krizhevsky
Die 10 Klassen sind die folgenden:
- 0 airplane
- 1 automobile
- 2 bird
- 3 cat
- 4 deer
- 5 dog
- 6 frog
- 7 horse
- 8 ship
- 9 truck
So lädt man die Daten in entsprechende Variablen:
from tensorflow.keras.datasets import cifar10
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train: ', x_train.shape)
print('y_train: ', y_train.shape)
print('x_test: ', x_test.shape)
print('y_test: ', y_test.shape)x_train: (50000, 32, 32, 3)
y_train: (50000, 1)
x_test: (10000, 32, 32, 3)
y_test: (10000, 1)Wir schauen uns wieder zwei Beispielbilder an. Um die Klassen abzugleichen, schauen Sie in die Liste oben.
print('Klasse ', y_train[0])
plt.imshow(x_train[0])Klasse [6]<matplotlib.image.AxesImage at 0x7fb5da20bc10>
print('Klasse ', y_train[1])
plt.imshow(x_train[1])Klasse [9]<matplotlib.image.AxesImage at 0x7fb60ebb1220>
Hier ein paar weitere Beispielbilder:
fig, ax = plt.subplots(nrows=2, ncols=4, figsize=(10, 10))
ax = ax.flatten()
for i in range(8):
ax[i].imshow(x_train[i])
ax[i].axis("off")
plt.tight_layout()
plt.show()
Abschließend sehen wir uns die Form der Labels an:
y_train[:10]array([[6],
[9],
[9],
[4],
[1],
[1],
[2],
[7],
[8],
[3]], dtype=uint8)9.3.3 CIFAR-100
Im CIFAR-100-Datensatz geht es darum, Farbbilder von Objekten zu klassifizieren. Es gibt 100 Klassen, die es vorherzusagen gilt, z.B. Shark, Clock, Road oder Woman. Es gibt auch 20 gröbere Klassen, die jeweils 5 Unterklassen enthalten. Die Bilder haben die Auflösung 32x32 und liegen in Farbe vor. Der Datensatz enthält 50000 Trainingsbeispiele und 10000 Testbeispiele.
Der Datensatz CIFAR-100 stammt von Alex Krizhevsky, Vinod Nair und Geoffrey Hinton.
Der Datensatz besteht wie CIFAR-10 aus 60000 32x32-Farbbildern, aber aus 100 Klassen. Die Beispiele sind gleichmäßig über die Klassen verteilt, d.h. es gibt (nur) 600 Beispiele pro Klasse. Es gibt 20 “grobe” Klassen, die jeweils in “feine” Unterklassen unterteilt sind. Die Klassifizierung in die 100 Klassen ist natürlich ein deutlich schwierigeres Problem als bei CIFAR-10 oder MNIST.
Auch hier lohnt sich ein Blick auf die Webseite von Alex Krizhevsky.
Die 20 groben Klassen mit den jeweiligen 5 Unterklassen sind:
- aquatic mammals: beaver, dolphin, otter, seal, whale
- fish: aquarium fish, flatfish, ray, shark, trout
- flowers: orchids, poppies, roses, sunflowers, tulips
- food containers: bottles, bowls, cans, cups, plates
- fruit and vegetables: apples, mushrooms, oranges, pears, sweet peppers
- household electrical devices: clock, computer keyboard, lamp, telephone, television
- household furniture: bed, chair, couch, table, wardrobe
- insects: bee, beetle, butterfly, caterpillar, cockroach
- large carnivores: bear, leopard, lion, tiger, wolf
- large man-made outdoor things: bridge, castle, house, road, skyscraper
- large natural outdoor scenes: cloud, forest, mountain, plain, sea
- large omnivores and herbivores: camel, cattle, chimpanzee, elephant, kangaroo
- medium-sized mammals: fox, porcupine, possum, raccoon, skunk
- non-insect invertebrates: crab, lobster, snail, spider, worm
- people: baby, boy, girl, man, woman
- reptiles: crocodile, dinosaur, lizard, snake, turtle
- small mammals: hamster, mouse, rabbit, shrew, squirrel
- trees: maple, oak, palm, pine, willow
- vehicles 1: bicycle, bus, motorcycle, pickup truck, train
- vehicles 2: lawn-mower, rocket, streetcar, tank, tractor
from tensorflow.keras.datasets import cifar100
(x_train, y_train), (x_test, y_test) = cifar100.load_data(label_mode='fine')
print('x_train: ', x_train.shape)
print('y_train: ', y_train.shape)
print('x_test: ', x_test.shape)
print('y_test: ', y_test.shape)x_train: (50000, 32, 32, 3)
y_train: (50000, 1)
x_test: (10000, 32, 32, 3)
y_test: (10000, 1)Hier ein paar Beispiele:
fig, ax = plt.subplots(nrows=2, ncols=4, figsize=(10, 10))
ax = ax.flatten()
for i in range(8):
ax[i].imshow(x_train[i])
ax[i].axis("off")
plt.tight_layout()
plt.show()
Die Labels sehen so aus:
y_train[:10]array([[19],
[29],
[ 0],
[11],
[ 1],
[86],
[90],
[28],
[23],
[31]])