14  Sprachverarbeitung

Wir begeben uns in die Welt der Sprachverarbeitung (Natural Language Processing, NLP). Im Vergleich zu unseren bisherigen Daten (z.B. Hauspreise oder Pixel von Bildern) handelt es sich bei Sprachdaten um sequentielle Daten, die Eingabe besteht aus Wörtern und Sätzen unterschiedlicher Länge. Wir lernen, wie man Wörter und Sätze repräsentiert und welche Vorverarbeitungsschritte man unternehmen muss (Tokenization). Dann lernen wir statistische Sprachmodelle kennen und sehen uns Word Embeddings an, mit denen man Wörter/Tokens als kompakte Vektoren repräsentieren kann. Word Embeddings kann man mit Neuronalen Sprachmodellen (NNLM) oder mit der Word2Vec-Methode trainieren.

Konzepte in diesem Kapitel

NLP, Vokabular, Token, Tokenizer, Wortindex, One-Hot-Encoding, Bag of Words, Word Embeddings, Sprachmodell, Unigramm, Bigramm, Neuronales Sprachmodell, word2vec

  • 01.04.2025: Word Embeddings überarbeitet

Datensatz

Name Daten Klassen Trainings-/Testdaten Ort
IMDB Text (Filmreviews) negativ (0), positiv (1) 25000/25000 14.6.3

14.1 Einleitung

In diesem Kapitel geht es um Sprachverarbeitung oder Natural Language Processing (kurz NLP). Aktuell ist Sprachverarbeitung durch Systeme wie ChatGPT sehr präsent und wird fast schon mit Künstlicher Intelligenz gleichgesetzt.

Sprachverarbeitung hat - ähnlich wie die Bildverarbeitung - ein lange Geschichte, in der unter dem Begriff Computerlinguistik viele klassische Methoden entwickelt wurden, die nicht mit Neuronalen Netzen oder Maschinellem Lernen zu tun haben (siehe z.B. Jurafsky and Martin 2008). Mittlerweile dominieren hier tatsächlich Neuronale Netze, insbesondere Transformer-Netze (Vaswani et al. 2017).

Typische Aufgabenstellungen in der Sprachverarbeitung sind:

  • Text-Klassifikation (Satz, Tweet, Dokument):
    • Ist eine e-Mail SPAM oder nicht?
    • Ist eine Rezension positiv oder negativ?
    • Enthält ein Tweet hate speech?
  • Klassifikation auf Wortebene:
    • Erkennung von Wortarten (z.B. Subjekt, Objekt, Verb), auch parts of speech genannt
    • Erkennung von Entitäten (z.B. Person, Ort, Institution), auch unter Named Entity Recognition bekannt
  • Text-Genereriung: Vervollständigen einer Eingabe mit automatisch generiertem Text, Ausfüllen der Lücken in einem Text mit verdeckten Wörtern
  • Question Answering, also das Beantwortung einer Frage zu einem gegebenen Text: Gegeben eine Frage und ein dazugehöriger Text (Kontext) soll eine Antwort auf die Frage aus dem Text extrahiert werden
  • Maschinelles Übersetzen: Aus dem Eingabetext in der Quellsprache soll ein neuer Satz in einer Zielsprache generiert werden
  • Automatisches Zusammenfassen: Aus dem Eingabetext soll ein neuer, kürzerer Text generiert werden, der möglichst viele Informationen aus dem Eingabetext enthält und korrekt wiedergibt

Die obigen Aufgaben gehen davon aus, dass eine sprachliche Äußerung bereits als Text vorliegt. Das Problem, eine Sprachäußerung in Audio-Form in einen Text zu überführen, nennt man auch Spracherkennung oder Speech Recognition (siehe z.B. Jelinek 1997).

Weitere Einsatzgebiete von NLP sind:

  • Multimodale Anwendungen: Zu einem gegebenen Bild automatisch eine Bildbeschreibung (Text) zu generieren oder umgekehrt aus einer Textbeschreibung ein Bild zu generieren.
  • Dialog und Konversation: Innerhalb eines sprachlichen Kontexts (i.d.R. ein Dialog) die nächste Äußerung generieren. Diese Aufgabe umfasst mehrere Disziplinen wie Speech Recognition, Natural Language Understanding oder Natural Language Generation.

Insbesondere das Thema “Dialog und Konversation” wurde durch ChatGPT auf unerwartete Weise vorangetrieben. Hier gab es lange Zeit wichtige Teildisziplinen der Computerlinguistik wie Natural Language Understanding, Natural Language Generation oder Dialogue Management, die durch den technologischen Sprung von ChatGPT und den darunterliegenden Methoden quasi überholt wurden.

14.2 Textdaten (Sequentielle Daten)

Wie kann man einen Text variabler Länge, z.B. den Satz “the cat sat on the mat”, einem neuronalen Netz zuführen? Der nächste Satz könnte weniger oder mehr Wörter enthalten. Solche Daten variabler Länge nennt man sequentielle Daten. Sie unterscheiden sich fundamental von Daten mit fixer Größe, z.B. Bildern mit der Auflösung 28x28.

14.2.1 Vokabular und Wortindex

Das führt zunächst zu der Frage, wie man ein einzelnes Wort wie “cat” oder “the” repräsentiert. Wir nehmen dabei an, dass es eine feste Menge von möglichen Wörtern gibt, also ein Vokabular \(V\). Mit \(|V|\) bezeichnen wir die Anzahl der Wörter in \(V\).

Wenn wir ein Vokabular \(V\) haben, dann ist jedes mögliche Wort mit einem eindeutigen Wortindex (Index) gelistet. Typischerweise sind alle Wörter alphabetisch sortiert und der Index ist einfach die Position in dieser Liste.

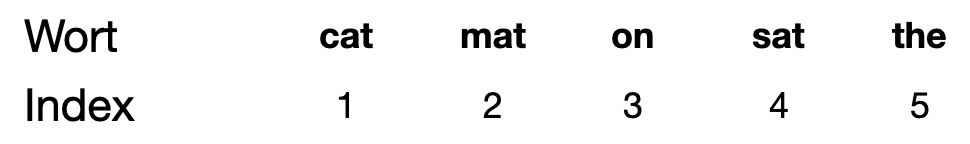
Die trivialste Möglichkeit, ein Wort numerisch für die maschinelle Verarbeitung zu repräsentieren, ist, jedes Wort mit seinem Index im Vokabular \(V\) zu repräsentieren. Also zum Beispiel 5 für “the”, 1 für “cat”, 2 für “mat” usw. Dann wäre der Satz “The cat sat on the mat” diese Folge von Zahlen [5, 1, 4, 3, 5, 2].

14.2.2 Tokens

Die Elemente von \(V\) (“cat”, “mat”…) nennt man auch Tokens. In unserem Beispiel sind es Wörter, aber in der Realität werden oft Wort-Teile genommen (sub-word tokens). Beispiele sind das Wort “Haustür”, das in die Tokens “Haus” und “Tür” zerlegt wird oder “Türen”, das in die Tokens “Tür” und “-en” zerlegt wird.

Ein Tokenizer ist ein Mechanismus (eine Software), um einen Text (eine Wort-Sequenz) in Tokens umzuwandeln. Bekannte Tokenizer sind Byte Pair Encoding (BPE), das bei GPT-2 und GPT-3 eingesetzt wird, oder WordPiece, der bei BERT zum Einsatz kommt.

Um ein Gefühl zu bekommen, wie ein echter Tokenizer funktioniert, können Sie den Tokenizer von OpenAI (der auch in ChatGPT eingesetzt wird) selbst im Browser ausprobieren, z.B. für den Satz “Die Katze saß auf der Matratze” (Tokens sind farblich abgesetzt):

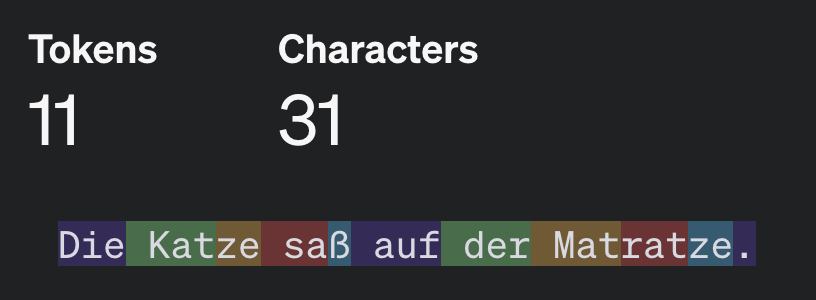
Tokenzier von OpenAI: Hier sind die Tokens eine Zwischenform zwischen Wortsilben und ganzen Wörtern; hier wird das sogenannte Byte pair encoding (BPE) verwendet.

Die Größe eines Vokabulars kann für kleine “Spielzeugsysteme” im Bereich 10.000 liegen, für echte Systeme ist aber eher im Bereich 100.000, 1 Million oder 100 Millionen realistisch.

Da die Größe von \(V\) begrenzt sein muss, enthält \(V\) in der Regel ein spezielles Token, das unbekannte Wörter repräsentiert. Dieses wird oft als <UNK> (für unknown) bezeichnet.

Je nach Anwendung sind noch spezielle Tokens für Satzzeichen oder für das Satzende <EOS> enthalten (für end of sentence), z.B. wenn man das Satzende vorhersagen möchte.

14.2.3 Problem mit dem Index

Das Problem mit dem Index als Repräsentation für ein Wort/Token ist, dass Ähnlichkeit von Wörtern nicht einer numerischen Ähnlichkeit (Distanz bzw. Differenz) entspricht. Das Wort “cat” ist zum Beispiel rein zufällig sehr nah an “mat”, obwohl es keine semantische Ähnlichkeit gibt. Wörter wie “dog” oder “tiger” sollten viel näher an “cat” sein. Diese Diskrepanz erschwert einem Neuronalen Netz die Arbeit und daher wird diese naive Methode heutzutage nicht verwendet.

Außerdem haben wir mit dieser Repräsentation noch nicht das Problem gelöst, einen Satz mit beliebiger Länge in ein Netz mit fixer Anzahl von Input-Neuronen einzuspeisen.

14.2.4 One-Hot Encoding für Tokens

Wir können unsere Wörter mit dem bekannten One-Hot-Encoding repräsentieren. Ein Wort \(w\) mit Index \(i\) wird als Vektor \(v = (0, 0, \ldots, 0, 1, 0, \ldots, 0)\) der Länge \(|V|\) repräsentiert. Vektor \(v\) hat genau eine 1 an der Stelle \(i\) und sonst Nullen. Man nennt solche Vektoren auch sparse.

Das Wort “cat” könnte so aussehen - bei einem sehr kleinen Vokabular mit \(|V|=5\):

\[\left( \begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \\ 0 \end{array} \right)\]

Schauen wir uns ein Beispiel für dieses kleine Vokabular an:

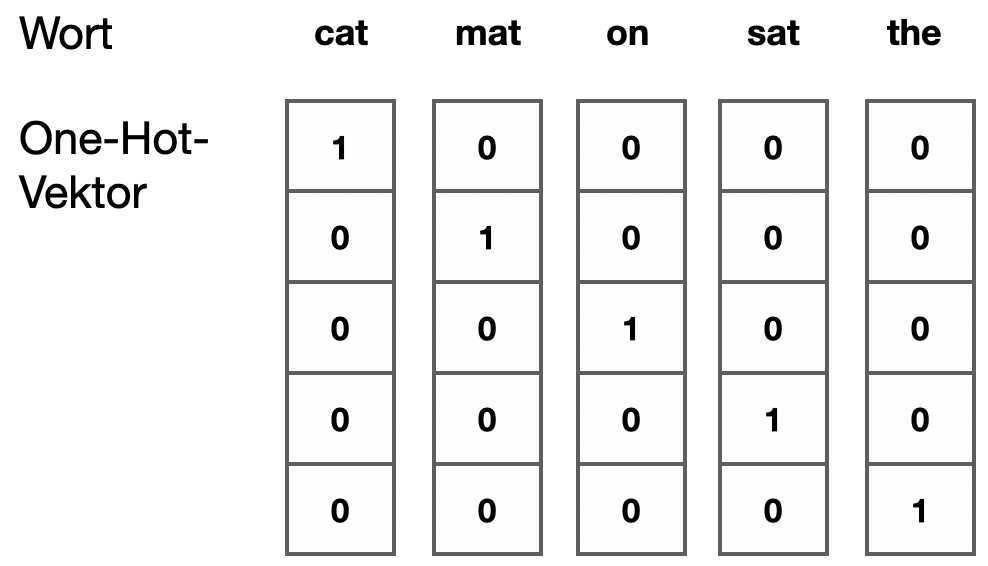
Wenn wir die Wörter einzeln einem Neuronalen Netz zuführen würden, hätten wir folgende Inputs für den Satz “the cat sat on the mat”:

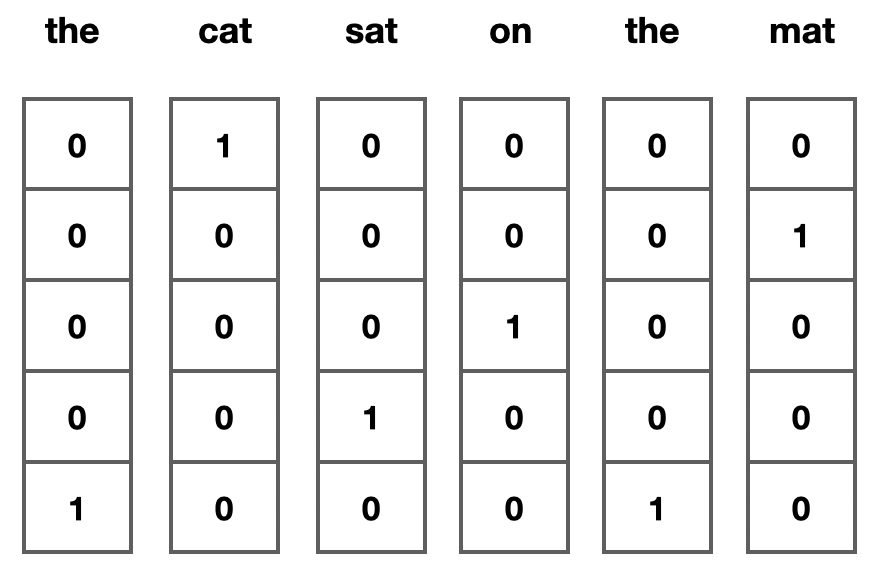
14.2.5 Bag of Words

Wenn wir für den ganzen Satz einen einzigen Output generieren möchten - z.B. SPAM oder Nicht-SPAM - dann haben wir hier ein Problem, denn wir generieren ja fünf Outputs. Außerdem ist jeder Output unabhängig von den anderen Outputs, d.h. man kann Zusammenhänge zwischen den Wörtern nicht abbilden.

Wie kodieren wir also einen ganzen Satz als Input für ein Netz mit fixer Eingabegröße? Ein Satz kann schließlich unterschiedlich lang sein.

Ein häufiger Ansatz ist es, einfach alle Wortvektoren zu addieren, so dass man immer einen aufsummierten Vektor der Länge \(|V|\) erhält. Diese Repräsentation nennt man Bag of Words, also ein “Sack voll Wörter”. Im Grunde spiegelt dieser Vektor die Häufigkeitsverteilung aller Wörter, die in dem Satz vorkommen, wider:

\[ \mbox{the cat sat on the mat} \quad\Rightarrow\quad \left( \begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \\ 2 \end{array} \right) \]

(Dieser Bag-of-Words-Vektor ist in der Regel auch “sparse”, d.h. es gibt z.B. 10000 Stellen, von denen nur einige wenige nicht gleich Null sind.)

Man beachte, dass die Information der Wortreihenfolge (wo steht welches Wort im Satz) verloren geht. Für viele einfache Anwendungen reicht es aber schon aus, nur das Vorkommen bestimmter Wörter zu verarbeiten, unabhängig davon, wie genau diese angeordnet sind. Man denke an SPAM-Detection oder eine einfache Kategorisierung von Textdokumenten. Man kann sich vorstellen, dass hier bestimmte Signalwörter eine größere Rolle spielen als die Reihenfolge (man spricht auch von Keyword Spotting). Umgekehrt gibt es natürlich viele Beispiele, wo die Reihenfolge der Wörter ausschlaggebend für die Bedeutung ist. Typische Beispiel sind Negationen, zum Beispiel “du, nicht ich” versus “nicht du, ich”. Beide Sätze haben eine identische Bag-of-Words-Repräsentation.

14.3 Statistische Sprachmodelle

Bevor wir uns mit Word Embeddings beschäftigen, müssen wir einen Exkurs unternehmen und lernen, was Sprachmodelle (engl. language models) sind.

14.3.1 Was sind Sprachmodelle?

Ein Sprachmodell ist ein Modell, das Vorhersagen treffen kann. Die Eingabe besteht aus einer Reihe von Wörtern. Ein Beispiel wäre:

Ich lese ein

Die Ausgabe ist das wahrscheinlichste nächste Wort. Bei unseren Beispiel könnte dies das folgende Wort sein:

Buch

Es könnte auch eine Reihe von möglichen Wörtern mit jeweils einer Wahrscheinlichkeit sein:

Buch, 0.82
Rezept, 0.10
Dokument, 0.05
Pamphlet, 0.03

Sprachmodelle sind sprach-spezifisch, d.h. für das Deutsche benötigt man offensichtlich ein anderes Modell als fürs Englische.

Der ursprüngliche Einsatz von Sprachmodellen war die Spracherkennung. Spracherkennung heißt: Gesprochene Sprachen wird übersetzt in geschriebene Wörter, also Text. Der Input besteht also aus einer Sequenz von Audiodaten (in Form einer Datei oder eines Streams), der Output besteht aus einer Sequenz von Wörtern (= Strings). Spracherkennung ist sehr fehleranfällig, besonders wenn schnell und/oder unartikuliert gesprochen wird.

Vergleichen Sie:

  • Ich kann nicht mehr / Ich kann ich Meer
  • Ich mag mit dem Rad fahren / Ich Mark mitten Rat Farn

Sprachmodelle können hier schnell Klärung schaffen, da viele Wortkombinationen grammatikalisch oder semantisch ausgeschlossen werden können.

14.3.2 Wie baut man ein Sprachmodell?

Die ersten Sprachmodelle waren probabilistischer Natur. Das Problem, das nächste Wort eines Teilsatzes vorherzusagen, wurde zunächst auf folgende Aufgabe reduziert:

Gegeben eine bestimmte Anzahl vorheriger Wörter, welches ist das wahrscheinlichste nächste Wort?

Der triviale Fall ist, dass man keine vorherigen Wörter betrachtet. Dann sagt man im Grunde immer das häufigste Wort voraus. Man würde dies aus einer Tabelle mit den Häufigkeiten aller Wörter ablesen können. Man nennt dieses triviale und offensichtlich wenig sinnvolle Modell auch ein Unigramm-Modell.

Betrachten wir jetzt immer genau ein vorheriges Wort, dann können wir ebenfalls eine Tabelle erstellen. Diesmal betrachten wir im Grunde Wortpaare \((v, w)\), wobei \(v\) das vorherige Wort und \(w\) das nachfolgende Wort ist. So ein Wortpaar nennt man auch ein Bigramm. Jetzt möchten wir zählen, wie oft \(w\) auf \(v\) folgt. Das nennt man die absolute Häufigkeit. Wenn wir diese Zahl durch die Anzahl der Vorkommen von \(w\) teilen, erhalten wir die relative Häufigkeit. Die relative Häufigkeit von \((v, w)\) entspricht der bedingten Wahrscheinlichkeit:

\[ P(v | w) \]

Sehen wir uns ein Beispiel an, wo wir nur die folgenden 8 Beispielsätze haben.

  • Der Hund spielt im Park.
  • Das Kind spielt gern im Park.
  • Der Hund und das Kind spielen.
  • Das Kind und der Hund laufen.
  • Der Hund läuft schnell im Park.
  • Das Kind spielt gern mit dem Hund.
  • Im Park spielen das Kind und der Hund.
  • Der Hund läuft gern.

Wir ersetzen ein paar Wörter durch Tokens:

  • Satzzeichen wie der Punkt werden entfernt
  • Artikel (“der”, “das”, “dem”) werden entfernt
  • Alle Wörter werden klein geschrieben
  • die Verbformen “laufen” und “läuft” werden durch laufen ersetzt, die Verbformen “spielen” und “spielt” durch spielen

Außerdem stellen wir die speziellen Tokens START und END an Anfang und Ende. Die Sätze sehen jetzt so aus:

  • START hund spielen im park ENDE
  • START kind spielen gern im park ENDE
  • START hund und kind spielen ENDE
  • START kind und hund laufen ENDE
  • START hund laufen schnell im park ENDE
  • START kind spielen gern mit hund ENDE
  • START im park spielen kind und hund ENDE
  • START hund laufen gern ENDE

Wir können jetzt eine Matrix erstellen, wo jede Zeile das vorherige Wort repräsentiert und jede Spalte das folgende Wort.

ENDE START gern hund im kind laufen mit park spielen und
ENDE 0 0 0 0 0 0 0 0 0 0 0
START 0 0 0 3 1 3 0 0 0 0 0
gern 1 0 0 0 1 0 0 1 0 0 0
hund 2 0 0 0 0 0 2 0 0 1 1
im 0 0 0 0 0 0 0 0 3 0 0
kind 0 0 0 0 0 0 0 0 0 3 2
laufen 1 0 1 0 0 0 0 0 0 0 0
mit 0 0 0 1 0 0 0 0 0 0 0
park 2 0 0 0 0 0 0 0 0 1 0
spielen 1 0 2 0 1 1 0 0 0 0 0
und 0 0 0 2 0 1 0 0 0 0 0

Die erste Zeile der Matrix zeigt, welche Tokens nach dem Token “ENDE” kommen. Es kommt natürlich nie ein weiteres Token, daher steht dort überall eine Null. Die zweite Zeile zeigt, welches Wort meist am Anfang steht. Da sind “hund” und “kind” die Spitzenreiter, da sie jeweils 3x am Anfang eines Satzes stehen. Man nennt diese Zahlen auch die absoluten Häufigkeiten. Die relative Häufigkeit kann man berechnen, wenn man jede Zahl durch die Zeilensumme teilt. In der Zeile “START” ist die Zeilensumme 7. Also ergeben sich folgende relative Häufigkeiten, die gleichzeitig eine Schätzung der bedingten Wahrscheinlichkeit ist:

\[ \begin{align} P(\mbox{START} | \mbox{hund}) &= \frac{3}{7} = 0.429 \\ P(\mbox{START} | \mbox{im}) &= \frac{1}{7} = 0.143 \\ P(\mbox{START} | \mbox{kind}) &= \frac{3}{7} = 0.429 \end{align} \]

14.4 Word Embeddings

Mittlerweile hat es sich zum Standard entwickelt, sogenannte Word Embeddings zu verwenden, um Wörter zu repräsentieren. Das ist sozusagen eine Zwischenlösung zwischen den beiden Möglichkeiten, die wir bislang betrachtet haben (Wortindex bzw. One-Hot-Vektor, siehe Abb. 14.1). Bei einem Vokabular \(V\) mit 20.000 oder 100.000 Wörtern sind One-Hot-Vektoren sehr ineffizient, da diese Vektoren hauptsächlich aus sehr vielen Nullen bestehen. Stattdessen wollen wir pro Wort einen Vektor mit deutlich weniger Einträgen, wo aber alle Elemente (Features) tatsächlich mit Werten belegt sind.

Hier sehen wir die drei Möglichkeiten, um das Wort “sat” zu repräsentieren:

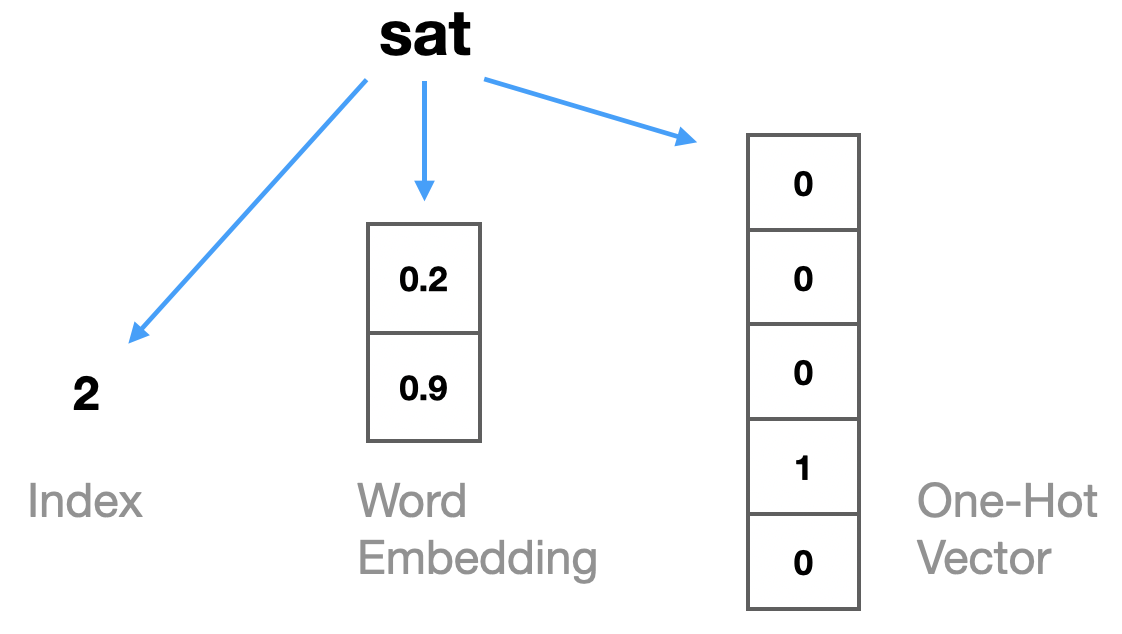
Figure 14.1: Das Wort “sat” in drei möglichen Repräsentationen, als Wortindex, als Embedding und als One-Hot-Vektor; hier haben wir allerdings nur ein Vokabular der Größe \(|V|=5\).

Wir geben eine beliebige Anzahl von Features \(m\) vor, z.B. \(m=2\), und möchten für jedes Wort eine Repräsentation als Vektor der Länge 2 finden. Die Werte dieses Feature-Vektors beschränken sich nicht auf 0 und 1, sondern können beliebige Dezimalzahlen sein. Wichtig ist, dass die Länge \(m\) der Word-Embedding-Vektoren deutlich geringer ist als die Größe des Vokabulars \(|V|\), zum Beispiel \(m=30\) bei einem Vokabular von \(|V| = 80000\).

Hier ein Beispiel mit \(m=2\):

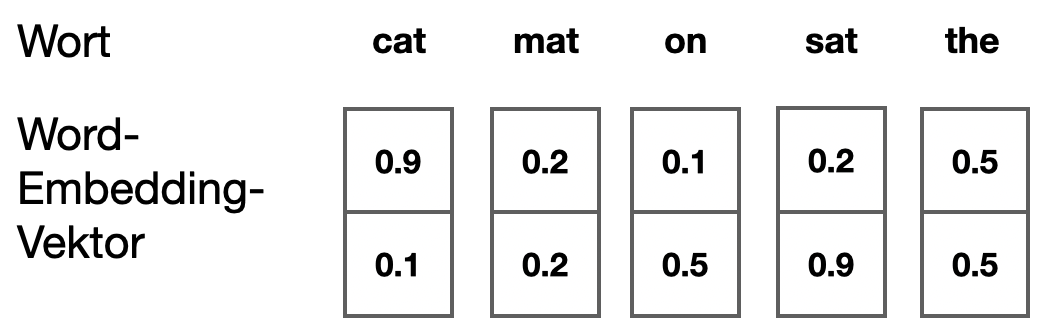
Jetzt werden diese Repräsentation aber gelernt und die Ähnlichkeiten stellen sich tatsächlich im Laufe des Lernens ein (wie das genau funktioniert, sehen wir im nächsten Abschnitt). Am Ende des Lernprozesses hat man eine “Tabelle” wie oben, wo man für jedes Wort die 4-dimensionale Kodierung (Einbettung) als Feature-Vektor der Länge \(m\) ablesen kann. Eine solche Tabelle nennt man auch eine Projektion in den Raum der Wörter (daher auch “embedding”: das Wort wird eingebettet in diesen neuen Wort-Raum).

Jede Dimension in der Abbildung oben nennt man Feature und man kann sich das als einen semantischen Aspekt des Worts vorstellen, der mit einem Wert zwischen 0 und 1 (oder einer anderen Skalierung) belegt ist. Mögliche Aspekte sind “belebt-unbelebt”. Es kann auch eine Formeigenschaft wie “kurz-lang” oder eine Bewegungseigenschaft wie “schnell-langsam” oder ein Persönlichkeitsmerkmal wie “introvertiert-extrovertiert” sein. Da die Embeddings gelernt werden, richtet sich die Repräsentation nach den Daten und dem Ziel der Klassifikationsaufgabe.

Was “bedeuten” die Dimensionen bzw. Features? Tatsächlich zeigen Word Embeddings, die mit Neuronalen Netzen gelernt wurden, bemerkenswerte Eigenschaften (Mikolov, Yih, and Zweig 2013). Im Vektorraum der Word Embeddings lassen sich Eigenschaften wie “weiblich” als Vektoren auffassen, die man auf andere Wortvektoren addieren kann, um deren Bedeutung zu modifizieren. Wenn wir mit Funktion \(W\) die word embedding denotieren, dann wäre z.B.

\[W(\mbox{Onkel}) + W(\mbox{weiblich}) = W(\mbox{Tante})\]

Den Vektor \(W(\mbox{weiblich})\) kann man wiederum als Differenzvektor zwischen zwei Begriffen verstehen:

\[W(\mbox{weiblich}) = W(\mbox{Frau}) - W(\mbox{Mann})\]

Dann kann man also Vektor-Arithmetik dieser Arbeit betreiben:

\[W(\mbox{Königin}) = W(\mbox{König}) + W(\mbox{Frau}) - W(\mbox{Mann})\]

Abbildung 14.2 zeigt die Relation “weiblich” (links) sowie die Relation “plural” (rechts).

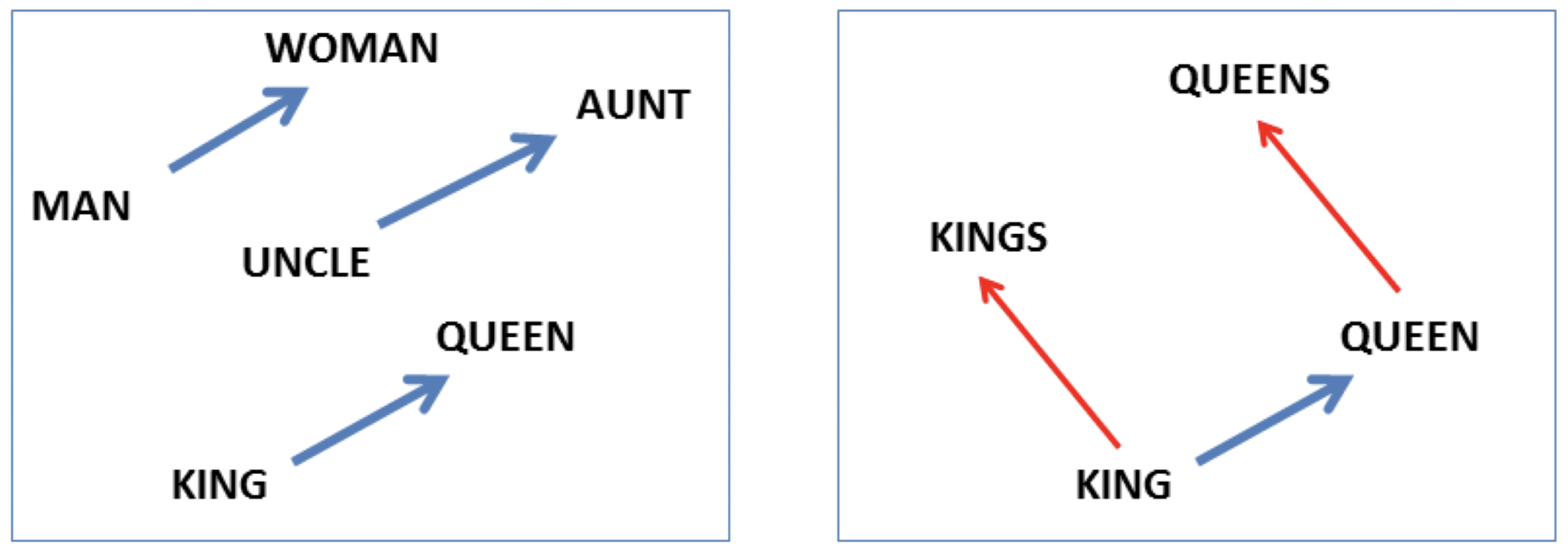
Figure 14.2: Quelle: (Mikolov, Yih, and Zweig 2013)

Beim Word Embedding unterscheidet man also zwischen Größe des Vokabulars \(|V|\) und der Anzahl der Features \(m\). In unserem Minibeispiel in Abb. 14.1 sind \(m=2\) und \(|V|=5\). In realen Anwendungen ist die Größe des Vokabulars \(|V|\) eher im Bereich 100.000 und die Anzahl der Features \(m\) im Bereich 30 bis 700.

14.5 Lernen von Word Embeddings

14.5.1 Neuronale Sprachmodelle (NNLM)

Neuronale Sprachmodelle (NNLM) wurden von Bengio et al. (2003) eingeführt, um Word Embeddings mit Hilfe einfacher Neuronaler Netze zu lernen. Die Word Embeddings sind hier das “Nebenprodukt” einer relativ simplen Trainingsaufgabe des Netzwerks. Diese Aufgabe ist, das jeweils nächste Wort in einem Satz vorherzusagen auf Basis der letzten \(n-1\) Wörter. Bei \(n=3\) nimmt man die letzten 2 Wörter, um das dritte vorherzusagen.

Als konkretes Beispiel: Bei diesem Satz

the cat sat on the mat

möchte man, dass das Modell folgende Vorhersagen vornimmt:

the cat -> sat
cat sat -> on
sat on -> the
on the -> mat

Im Beispiel haben wir \(n=3\) angenommen. Das \(n\) bezieht sich auf die drei Wörter, die involviert sind. Ein Wort ist das Wort, das vorherzusagen ist. Die anderen beiden sind der Kontext.

Dieses Problem löst man normalerweise mit Hilfe von Statistik, indem man einfach die Häufigkeit von Wortfolgen zählt und damit die bedingte Wahrscheinlichkeit \(P(w_t | w_{t-2}, w_{t-1})\) schätzt, wie in Abschnitt 14.3 erklärt.

Wir sehen diese Aufgabe aber nur als Mittel zum Zweck. Unser Ziel ist es, jedes Wort (oder Token) aus dem Vokabular \(V\) mit einem Vektor der Länge \(m\) zu repräsentieren. Dabei soll \(m\) deutlich kleiner sein als \(|V|\). Beispielhafte Werte sind \(|V| = 17000\) und \(m=30\) (aus Bengio et al. 2003).

Jetzt betrachten wir das Neuronale Netz. Bei \(n=3\) geben wir zwei Wörter, jeweils als One-Hot-Encoding mit Länge \(|V|\), in das Netz ein. Die Matrix \(C\) bildet jedes Wort auf einen Vektor der Länge \(m\) ab, so dass die erste Schicht hier die Länge \(2 \cdot m\) hat. Dann gibt es eine Zwischenschicht der Länge \(p\) und eine Ausgabe der Länge \(|V|\), wo mit Softmax eine Wahrscheinlichkeitsverteilung als Vorhersage für das nächste Wort ausgegeben wird.

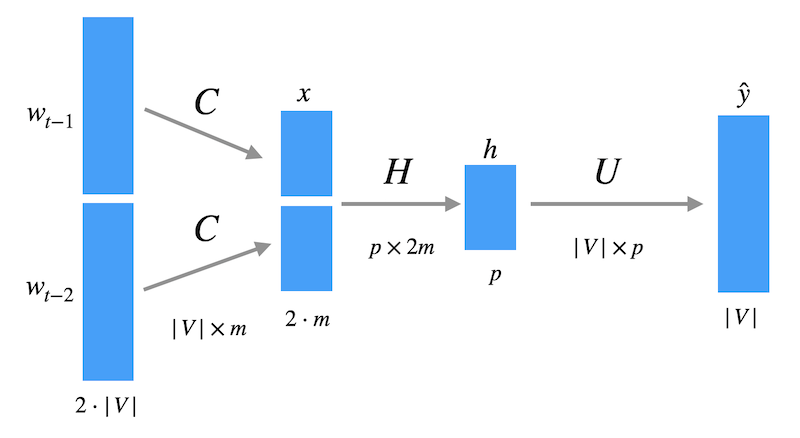
Das Mapping von One-Hot-Vektor zu Feature-Vektor wird mit einer Matrix \(C\) der Größe \(|V| \times m\) realisiert. Formal ist das eine Matrixmultiplikation, wir betrachten das hier nur für ein Wort \(w\) und der Ausgabe \(x\):

\[ x = w^T \, C \]

Die obige Multiplikation wird tatsächlich durch ein einfaches “Look-up” realisiert, da man mit Hilfe des Wortindex \(i\) einfach die \(i\)-te Zeile von \(C\) herausziehen kann. Die Matrix \(C\) wird beim Training auf die Vorhersageaufgabe mit Backprop immer wieder angepasst und es stellt sich heraus, dass nach Training sehr aussagekräftige Repräsentationen der Wörter in \(C\) stehen.

14.5.2 Word2Vec

Einem aktuelleren Ansatz namens Word2Vec (Mikolov et al. 2013), entwickelt von Google, liegt die Idee zugrunde, dass nicht aufeinander folgende Wörter betrachtet werden, sondern beliebige Wörter. In einem Satz wird also ein Wort zufällig herausgepickt, welches vorhergesagt werden soll (Target), und ein weiteres zufälliges Wort (oder mehrere) in dem Satz wird als “Hinweis” ausgewählt (Kontext). Dieses Verfahren ist nochmal effizienter als das von Bengio et al. (2003).

14.6 Keras: Tools und Daten für NLP

14.6.1 Tokenizer

Ein Tokenizer ist ein Programm, das Texte in Tokens zerlegt. In unserem Fall sind die Tokens alle Wörter, wobei Groß-/Kleinschreibung ignoriert wird. Satzzeichen sind keine Tokens und werden ignoriert.

In Keras wird ein Tokenizer auf einer Menge von Texten “trainiert” mit fit_on_words. Der Tokenizer baut einen Wortindex auf: jedes Wort (= Token) wird mit einer eindeutigen Zahl assoziiert.

s1 = 'Harry ging nach Berlin, ich nicht.'
s2 = 'Ich ging nach Hause?'

texte = [s1, s2]

Man gibt dem Tokenizer i.d.R. über num_words eine Grenze \(M\) mit, wie viele Tokens aufgenommen werden sollen. Es werden dann nur die \(M\) häufigsten Tokens verwendet (im Wortindex sind dennoch alle Wörter vertreten, aber später in den Sequenzen nicht mehr).

from tensorflow.keras.preprocessing.text import Tokenizer

tok = Tokenizer(num_words=4)
tok.fit_on_texts(texte)

tok.word_index
{'ging': 1,
 'nach': 2,
 'ich': 3,
 'harry': 4,
 'berlin': 5,
 'nicht': 6,
 'hause': 7}

Hier sehen wir, dass “Ich” und “nicht” repräsentiert werden, aber nicht “nicht”, weil dieses Wort nicht unter den 4 häufigsten Wörtern war.

tok.texts_to_sequences(['Ich ging nicht dorthin.'])
[[3, 1]]

Jetzt können wir das als Bag-of-words-Repräsentation ausgeben. Dies ist ein Vektor der Länge 4. Nur bei solchen Indizes, bei denen das entsprechende Wort im Satz vorkommt, steht eine Zahl (z.B. 1), bei allen anderen Null.

Im Modus binary steht bei den vorkommeneden Wörtern eine 1, egal wie häufig sie vorkommen. Hier sehen wir zwei Einträge für “ich” und “ging”.

tok.texts_to_matrix(['Ich ging nicht dorthin, aber er ging.'], mode='binary')
array([[0., 1., 0., 1.]])

Im Modus count steht die Häufigkeit der Vorkommen als absolute Häufigkeit (hier die 2 für “ging”).

tok.texts_to_matrix(['Ich ging nicht dorthin, aber er ging.'], mode='count')
array([[0., 2., 0., 1.]])

Im Modus freq wird die relative Häufigkeit genommen, d.h. die Zahl der Vorkommen von Wort \(w\) wird durch die Gezamtzahl aller vorkommenden Wörter geteilt (hier einmal 2/3 für “ging” und einmal 1/3 für “ich”).

tok.texts_to_matrix(['Ich ging nicht dorthin, aber er ging.'], mode='freq')
array([[0.        , 0.66666667, 0.        , 0.33333333]])

14.6.2 Padding bei Sequenzen

Um eine fixe Sequenzlänge zu erzwingen, gibt es die Keras-Funktion pad_sequences.

Eine Sequenz ist hier eine Reihe von Zahlen. Wir stellen zwei Sequenzen mit Hilfe unseres Tokenizers her.

seq = tok.texts_to_sequences(texte)
seq
[[1, 2, 3], [3, 1, 2]]

Hier kürzen wir die Sequenzen auf Länge 2.

from tensorflow.keras.preprocessing import sequence

sequence.pad_sequences(seq, maxlen=2)
array([[2, 3],
       [1, 2]], dtype=int32)

Hier erweitern wir die Sequenzen, so dass sie Länge 5 haben.

sequence.pad_sequences(seq, maxlen=5)
array([[0, 0, 1, 2, 3],
       [0, 0, 3, 1, 2]], dtype=int32)

Eine gute Darstellung findet man in dem Artikel Data Preparation for Variable Length Input Sequences.

14.6.3 IMDB-Datensatz in Keras

IMDB-Datensatz

Der IMDB-Datensatz enthält 25.000 Filmrezensionen (IMDb steht für Internet Movie Database). Für jede Rezension besteht aus einem Text und hat einen Label, der besagt, ob die Rezension positiv oder negativ war. Man kann den Datensatz also für binäre Klassifikation verwenden (man nennt diese Art Klassifikation aus sentiment classification). Die Wörter sind mit Indexzahlen kodiert. Die Indexzahl ergibt sich aus der Häufigkeit eines Worts. Das Wort mit Index 5 ist also das 5. häufigste Wort in der Datenbank. Siehe auch die Keras-Doku. Wir zeigen in Abschnitt 15.3.1 nochmal eine praktische Anwendung.

Schauen wir uns die Prinzipien von One-Hot-Encoding am Beispiel des IMDB-Datensatzes an.

Beim Laden kann man die Größe des Vokabulars angeben. Wir geben hier zum Testen 20 an, d.h. nur die 20 häufigsten Wörter werden ins Vokabular aufgenommen, dass entsprechend die Größe 20 hat.

from tensorflow.keras.datasets import imdb
from tensorflow.keras.preprocessing import sequence

(train_x, train_y), (test_x, test_y) = imdb.load_data(num_words=20)

print(f'{train_x.shape}, {test_x.shape}')
(25000,), (25000,)

Der Datensatz enthält Sätze als Zahlenreihen. Die “2” steht für ein Wort, das nicht im Vokabular enthalten ist.

train_x[0][:20]
[1, 14, 2, 16, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 4, 2, 2, 2, 5, 2]

Ein Wortindex erlaubt uns zu sehen, welches Wort zu welcher Zahl gehört.

[(w, i) for w, i in imdb.get_word_index().items()][:10]
[('fawn', 34701),
 ('tsukino', 52006),
 ('nunnery', 52007),
 ('sonja', 16816),
 ('vani', 63951),
 ('woods', 1408),
 ('spiders', 16115),
 ('hanging', 2345),
 ('woody', 2289),
 ('trawling', 52008)]

Wir schauen uns den ersten Satz in den Trainingsdaten an und konvertieren die Wörter zu einer One-Hot-Encoding.

import numpy as np
from tensorflow.keras.utils import to_categorical

s = to_categorical(train_x[0], num_classes=20)
print(len(s))
s
218
array([[0., 1., 0., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 0.],
       [0., 0., 1., ..., 0., 0., 0.],
       ...,
       [0., 0., 0., ..., 0., 0., 1.],
       [0., 0., 1., ..., 0., 0., 0.],
       [0., 0., 1., ..., 0., 0., 0.]], dtype=float32)

Um den Bag-of-Words-Vektor zu berechnen, addieren wir alle Vektoren, und erhalte so einen fixen Input der Länge 20. Mit diesem Input könnte man ein konventionelles Feedforard-Netz trainieren.

np.sum(s, axis=0)
array([  0.,   1., 149.,   0.,  15.,   9.,   3.,   2.,   3.,   1.,   0.,
         0.,   6.,   3.,   3.,   4.,  11.,   3.,   3.,   2.],
      dtype=float32)

Wir haben hier noch keine Word Embeddings gesehen. Wir werden aber Embedding-Schichten demnächst kennen lernen, wenn wir uns wieder Keras zuwenden.

Verständnisfrage

Was kommt heraus, wenn Sie Achse 1 verwenden?

np.sum(s, axis=1)

Überlegen Sie erst, bevor Sie es ausprobieren.