import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt2 Maschinelles Lernen
In diesem Kapitel verschaffen wir uns einen Überblick über das Gebiet des Maschinellen Lernens. Wir lernen die Typen des Maschinellen Lernens kennen. Da wir uns ausschließlich mit Supervised Learning (Überwachtes Lernen) beschäftigen, betrachten wir ein Regressionsverfahren als Beispiel. Wir implementieren das Verfahren der linearen Regression direkt in Python und lernen anschließend die Anwendung des bereits implementierten linearen Regressors in der Bibliothek Scikit-learn kennen. Wir befassen uns mit dem Problem des Overfittings beim Training und der Einteilung der Daten in Trainings-, Test- und Validierungsdaten.
Supervised Learning, Modell, Eingabe-Features, Zielfunktion, lineare Regression, Gradientenabstieg, Epoche, Hyperparameter, Overfitting, Trainings-/Test-/Validierungsdaten
Nach Abschluss des Kapitels können Sie
- die verschiedenen Typen des Lernens (Supervised Learning, Reinforcement Learning etc.) und den Unterschied zwischen Regression und Klassifikation erklären
- lineare Regression erklären (Problemstellung, Modell, Parameter)
- Gradientenabstieg als Optimierungsmethode zur linearen Regression erklären
- erweiterte Regressionstechniken, wie Polynom- oder Mehrfachregression erklären
- Pythoncode zur linearen Regression erklären und gezielt anpassen
- das Problem des Overfitting erklären und Strategien zur Vermeidung von Overfitting aufzeigen
- die Begriffe Trainings-, Test- und Validierungsdaten definieren und können den Begriff Hyperparameter erklären
Datensatz
California housing dataset: Abschnitt 2.3.1
Importe
Diese Webseiten basieren auf Jupyter-Notebooks, daher benötigen wir einige Importe für Python. Zu Beginn eines Kapitels stehen daher die für die späteren Code-Teile benötigten Importe von Bibliotheken, hier z.B. Bibliotheken fürs Datenhandling (NumPy und Pandas) und zum Visualisieren (Matplotlib).
2.1 Überblick
In diesem Kapitel wollen wir uns einen Überblick über einfache Methoden des Maschinellen Lernens (ML) verschaffen. Beim ML geht es immer darum, ein Modell durch Daten und Lernmechanismen zu optimieren.
2.1.1 Typen des Maschinellen Lernens
Wir unterscheiden fünf Typen des maschinellen Lernens:
- Überwachtes Lernen (Supervised Learning)
- Unüberwachtes Lernen (Unsupervised Learning)
- Semi-überwachtes Lernen (Semi-supervised Learning)
- Selbstüberwachtes Lernen (Self-supervised Learning)
- Bestärkendes Lernen (Reinforcement Learning)
Überwachtes Lernen (Supervised Learning)
Beim überwachten Lernen gibt es gelabelte Trainingsdaten, d.h. man hat Paare \((x^k, y^k)\) von Eingabefeatures \(x^k\) und korrekter Ausgabe \(y^k\). Die Ausgabe \(y^k\) ist das jeweilige “Label” (oder die Klasse oder die Kategorie) des \(k\)-ten Trainingsbeispiels. Man benutzt die Trainingsdaten, um das Modell anzupassen und zu optimieren. Optimierung heißt, dass die Differenz (Fehler) zwischen Ausgabe des Modells und korrekter Ausgabe möglichst gering ist. In dieser Vorlesung geht es hauptsächlich um überwachtes Lernen.
Wir verwenden den hochgestellten Index (wie in \(w^k\)), um ein einzelnes Trainingsbeispiel zu kennzeichnen (z.B. \(w^2\) für das zweite Trainingsbeispiel). Es handelt sich nicht um Potenzierung. Natürlich gibt es da etwas Verwechslungspotential, aber leider gibt es nur endlich viele Orte für Indizes…

Unüberwachtes Lernen (Unsupervised Learning)
Beim unüberwachten Lernen sind die Trainingsdaten ungelabelt, d.h. man hat nur Features \((x^k)\). Das Lernverfahren bildet aufgrund der Daten eigene Kategorien (Cluster) bzw. erlaubt es, die Features auf eine kleinere Menge von Features zu reduzieren, die besonders gut zur Trennung der Trainingsdaten geeignet sind.
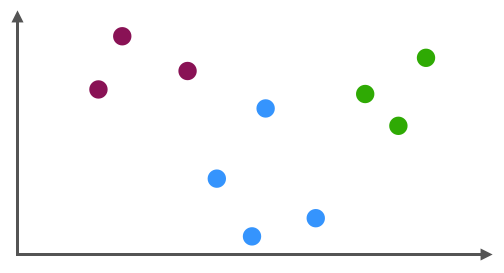
Methodisch sind die Bereiche des Supervised Learning und des Unsupervised Learning sehr verschieden. Das Skript enthält ein (optionales) Kapitel, wo ganz kurz auf Unsupervised Learning mit Neuronalen Netzen eingegangen wird, um diesen Unterschied zu illustrieren.
Semi-überwachtes Lernen (Semi-supervised Learning)
Beim semi-überwachten Lernen ist sowohl eine eher geringe Menge gelabelter Daten gegeben sowie eine große Menge ungelabelter Daten. Mit Hilfe von Verfahren des unüberwachten Lernens versucht man, die Kategorien der gelabelten Daten auf die ungelabelten Beispiele zu übertragen.
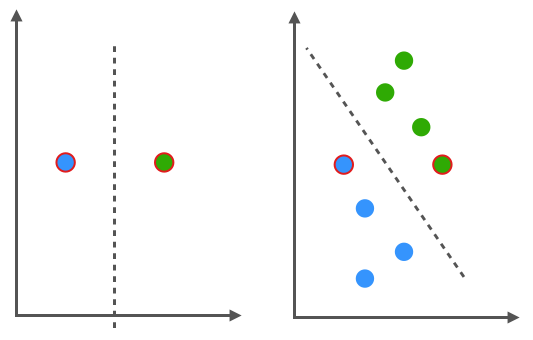
Selbstüberwachtes Lernen (Self-supervised Learning)
Self-supervised Learning ist besonders in der Sprachverarbeitung (NLP) und in diesem Zusammenhang natürlich mit aktuellen Technologien wie Transformer, GPT und ChatGPT relevant.
Beim selbstüberwachten Lernen möchte auf ungelabelten Daten die Methoden des überwachten Lernens anwenden. Wie funktioniert das? Man nimmt eine Menge an ungelabelten Daten und “versteckt” einen bestimmten Aspekt. Diesen Aspekt nimmt man als Label.
Beispiele aus der Bildverarbeitung
Nehmen wir an, wir möchten für ein beliebiges Schwarzweiß-Foto die Farben automatisch “vorhersagen”. Als Daten liegt eine Menge an Farbfotos ohne Labels vor.
Jetzt überführt man die Farbfotos in Schwarzweißbilder (Inputdaten). Die Farbinformation wird zum Label erklärt. Man kann ein Modell trainieren, das für Schwarzweiß-Fotos die Farbinformation vorhersagt (Zhang, Isola, and Efros 2016). Mit einem solchen Modell kann man dann alte Schwarzweiß-Bilder kolorieren.
Ein anderes Beispiel: Man nimmt ein Foto und generiert drei neue Fotos, indem man das Foto um 45°, 90° und 180° dreht. Die Aufgabe des Modells ist es, die Originalausrichtung zu erraten. Da man selbst die Änderung vorgenommen hat, kann man die Fotos entsprechende labeln (das Originalfoto mit “korrekt” und die gedrehten mit “falsch”). Ein trainiertes Modell kann dann für ein beliebiges Foto vorhersagen, ob die Orientierung korrekt oder falsch ist.
Beispiel aus der Sprachverarbeitung
Ein typisches Beispiel aus der Sprachverarbeitung ist folgendes Szenario: Man nimmt einen Satz (ohne Label), zum Beispiel
Ich war gestern früh beim Bäcker.
Aus diesem Satz kann man viele Traningsbeispiele generieren, um zum Beispiel immer das nächste Wort vorherzusagen:
- Input: “Ich” \(\longrightarrow\) Output: “war”
- Input: “Ich war”\(\longrightarrow\) Output: “gestern”
- Input: “Ich war gestern” \(\longrightarrow\) Output: “früh”
Diese Aufgabe klingt für sich genommen vielleicht nicht besonders spannend. Man benutzt Aufgaben wie diese aber häufig nicht, um wirklich eine Vorhersagemaschine zu bauen, die das nächste Wort vorhersagt, sondern um die Parameter des so trainiertes Netzwerks als Repräsentationen für Wörter (bzw. Tokens) zu verwenden. Diese Repräsentationen nennt man word embeddings. Mehr dazu gibt es in Kapitel 14.
Einordnung
Im Vergleich zum semi-überwachten Lernen hat man beim self-supervised Learning also keine Teilmenge an gelabelten Daten, sondern man nimmt die Labels aus den Daten selbst.
Obwohl die Ausgangslage (ungelabelte Daten) das selbstüberwachte Lernen in die Nähe des Unsupervised Learning rückt, sind die Methoden natürlich exakt die gleichen wie beim Supervised Learning.
Wen die Methode interessiert, kann ich folgenden Überblicksartikel von Lilian Weng empfehlen - auch mit Blick auf aktuelle Forschung: Self-Supervised Representation Learning. Außerdem gibt es ein ca. 1-stündiges Video Self-supervised Learning, ein Tutorial von Licheng Yu, Yen-Chun Chen und Linjie Li auf der CVPR2020-Konferenz.
Bestärkendes Lernen (Reinforcement Learning)
Beim bestärkenden Lernen werden Techniken des überwachten Lernens genutzt, um in einer Umwelt (repräsentiert durch einen Zustand) mit entsprechenden Umweltreizen (Belohnung/Bestrafung, engl. Reward) das Verhalten zu optimieren. Hier spricht man von einem Agenten. Das Modell bekommt als Input den aktuellen Zustand und gibt als Ausgabe die nächste Handlung (Aktion) aus. Die Belohnung/Bestrafung wird für das Lernen verwendet und kann nach jeder einzelnen Aktion oder nach einer Reihe von Aktionen erfolgen.
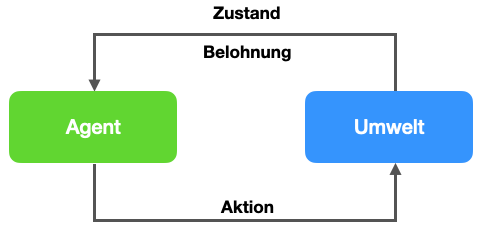
Reinforcement Learning wurde durch spektakuläre Erfolge im Bereich Computerspiele bekannt. AlphaGo Zero und AlphaZero können Spiele wie Schach lernen, in dem sie im Self-Play gegen sich selbst spielen (Silver et al. 2017). Eine Variante wurde im Self-Play trainiert, um alte Atari-Spiele wie Breakout zu lernen (Mnih et al. 2013). Weitere Erfolge gab es in der Robotik, z.B. beim Erlernen von komplexen und hochgradig kontext-abhängigen Bewegungsmustern (z.B. Lee et al. 2020; Gao et al. 2020).
In der Sprachverarbeitung rund um GPT und ChatGPT wurde ein Verfahren namens Reinforcement Learning from Human Feedback (RLHF) eingesetzt, um ein Fine-Tuning der Sprachmodelle zu erreichen (Ouyang et al. 2022). Mehr dazu finden Sie in einem Blogartikel Illustrating Reinforcement Learning from Human Feedback auf HuggingFace.
Reinforcement Learning werden wir in dieser Vorlesung nicht weiter behandeln können. Wenn Sie etwas dazu lesen wollen, ist das Standardwerk von Sutton and Barto (2018) zu empfehlen. Weiterhin gibt es einen Online-Kurs Reinforcement Learning - Goal Oriented Intelligence von DeepLizard. Wer gleich praktisch einsteigen möchte, sei die Umgebung Gymnasium empfohlen (ehemals OpenAI Gym), wo man Sofwareagenten in Python in Umgebungen testen kann, die RL benötigen.
2.1.2 Regression vs. Klassfikation
Wir gehen hier auf zwei einfache Verfahren des überwachtes Lernens ein:
- Regression: Auf Basis von Eingabefeatures wird eine Zahl geschätzt (z.B. Kaufpreis)
- Klassifikation: Auf Basis von Eingabefeatures wird ein Label vorhergesagt (z.B. Katze/Nicht-Katze)
Hier sehen wir schematisch ein Modell für Regression (oben) und eines für Klassifikation (unten):
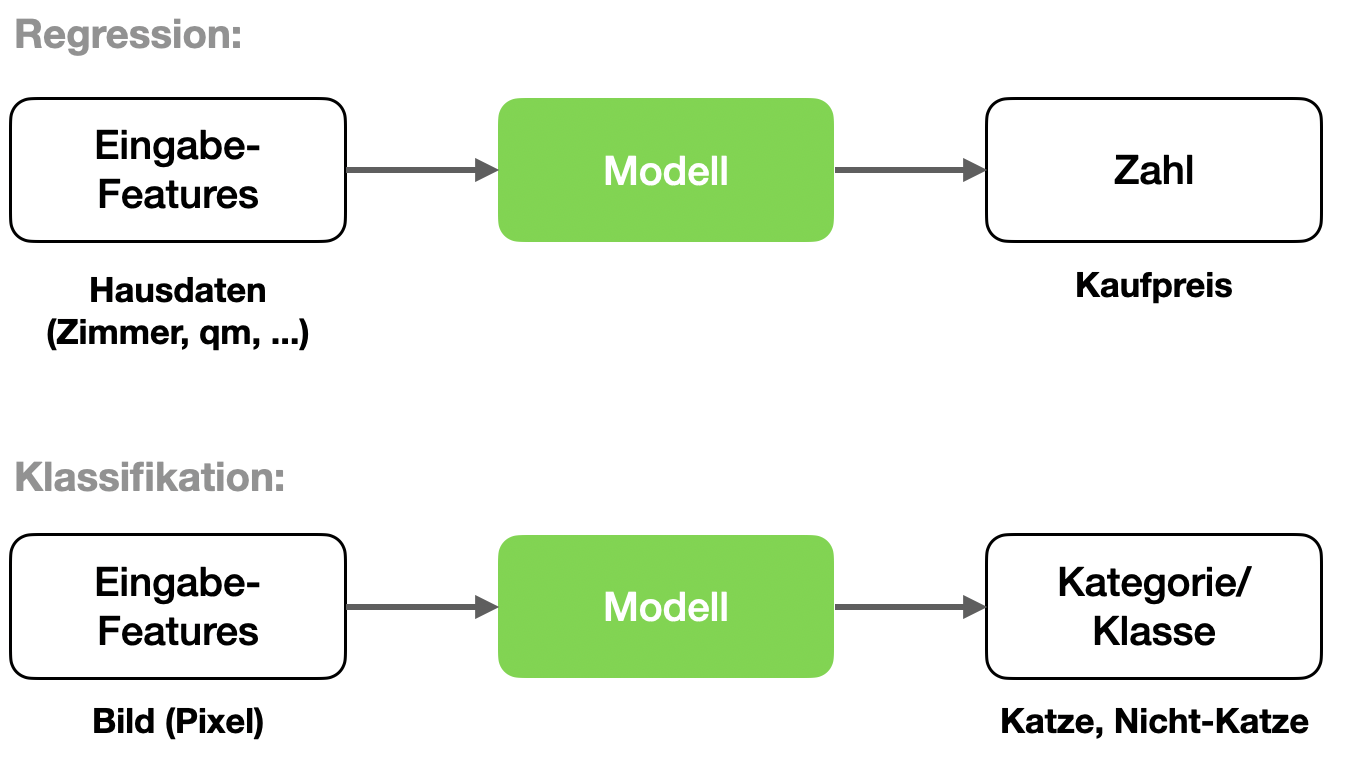
Wir beginnen mit Regression.
2.2 Lineare Regression
Bei der linearen Regression trainieren wir ein Modell, das es erlaubt, anhand von Eingabedaten eine Zahl vorherzusagen.
2.2.1 Problemstellung
Wir haben einen Datensatz von \(N\) gelabelten Trainingsbeispielen \((x^{k}, y^{k})\) mit \(k = 1, \ldots, N\). Der Index \(k\) kennzeichnet ein Trainingsbeispiel.
Jedes \(x \in \mathbb{R}^D\) ist ein \(D\)-dimensionaler Feature-Vektor und \(y \in \mathbb{R}\) der entsprechende Zielwert. Da das \(y\) ein echter, kontinuierlicher Wert ist, ist die Bezeichnung “gelabelte Beispiele” etwas irreführend, da es kein “Label” im Sinne einer Kategorie ist. “Gelabelt” bedeutet hier, dass der Zielwert bekannt ist.
Ein typisches Beispiel ist der Wert von Häusern. Der Vektor \(x = (x_1, x_2, \ldots, x_D)\) repräsentiert verschiedene Haus-Eigenschaften wie Wohnfläche in qm, Anzahl der Zimmer und Größe des Grundstücks in qm. Der Wert \(y\) repräsentiert den Kaufpreis, zum Beispiel in Tausend Euro (z.B. “321” für 321000 Euro).
Der tiefgestellte Index bezeichnet eine Komponente (ein Element) eines Vektors wie etwa \(x_2\) oder einer Matrix wie etwa \(m_{3,1}\) (dort entsprechend zwei Indizes für Zeile und Spalte).
In unserem späteren Beispiel ist \(x^k\) aber eine einfache Zahl, also ein Skalar und kein Vektor, d.h. wir haben nur ein einziges Feature, aufgrund dessen wir den Wert \(y\) vorhersagen möchten. Man nennt dies dann auch einfache lineare Regression. In Abbildung 2.1 sieht man ein Beispiel. Hier haben wir ein einziges Feature “Einkommen” und den Zielwert “Hauspreis”. Ein Trainingsbeispiel wie \((x^1, y^1)\) ist also ein einfacher Vektor mit zwei Skalaren.
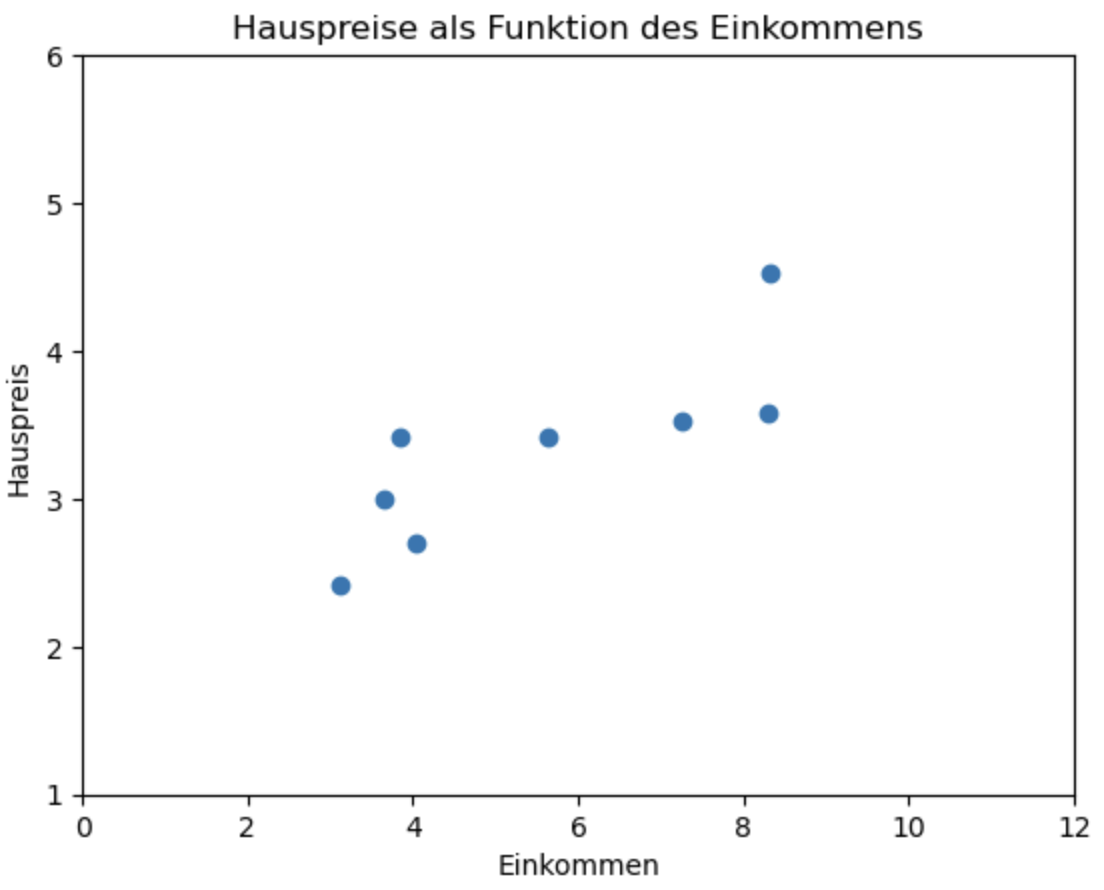
2.2.2 Modell und Parameter
Die Grundannahme ist jetzt, dass es eine ideale Funktion \(h^*\) gibt, die für jeden möglichen Eigenschaftsvektor \(x\) (Feature-Vektor) eines Hauses den “wahren” Wert des Hauses zurückgibt. Der Buchstabe “h” kommt von “Hypothese” bzw. hypothetische Funktion.
\(h^*\) ist also eine Abbildung der Art
\[ h^*: \mathbb{R}^D \rightarrow \mathbb{R} \]
Gesucht ist jetzt ein sogenanntes Modell, das sich dieser idealen Funktion \(h^*\) möglichst gut annähert. Wir nennen diese Modell \(h\), das ist natürlich ebenfalls eine Funktion \(h: \mathbb{R}^D \rightarrow \mathbb{R}\). Das \(h\) steht für engl. hypothesis (Hypothese) und soll zeigen, dass die Funktion eine Vermutung über die Wirklichkeit darstellt.
Die Funktion \(h\) beinhaltet eine Reihe von Parametern \(w = (w_0, w_1, \ldots, w_D) \in\mathbb{R}^{D+1}\). Da \(h\) von diesen Parametern abhängt, nennen wir die Funktion \(h_w\). Wir lassen das kleine \(w\) aber häufig aus Gründen der Lesbarkeit weg.
Das \(w\) kommt von engl. weight (Gewicht) und deutet auf die spätere Verwendung bei Neuronalen Netzen hin. In der Literatur wird auch oft der griechische Buchstabe \(\theta\) (Theta) benutzt, um Parameter zu repräsentieren.
Im einfachsten Fall kann man \(h_w(x)\) als Linearkombination der Komponenten von \(x\) plus einer Konstanten \(w_0\) auffassen:
\[ h_w (x) = w_0 + w_1 x_1 + \ldots + w_D x_D \]
Wenn \(x\) kein Vektor, sondern ein Skalar ist, wird daraus eine einfache Gerade (lineare Funktion):
\[ h_w (x) = w_0 + w_1 x \]
wobei \(w_0\) den y-Achsenabschnitt darstellt und \(w_1\) die Steigung. Abbildung 2.2 zeigt eine solche Gerade als Modell für unser Beispiel. Mit Hilfe dieser Geraden können wir jetzt für ein beliebiges Haus aus Basis des Einkommens in der Hausgegend den voraussichtlichen Hauspreis ablesen.
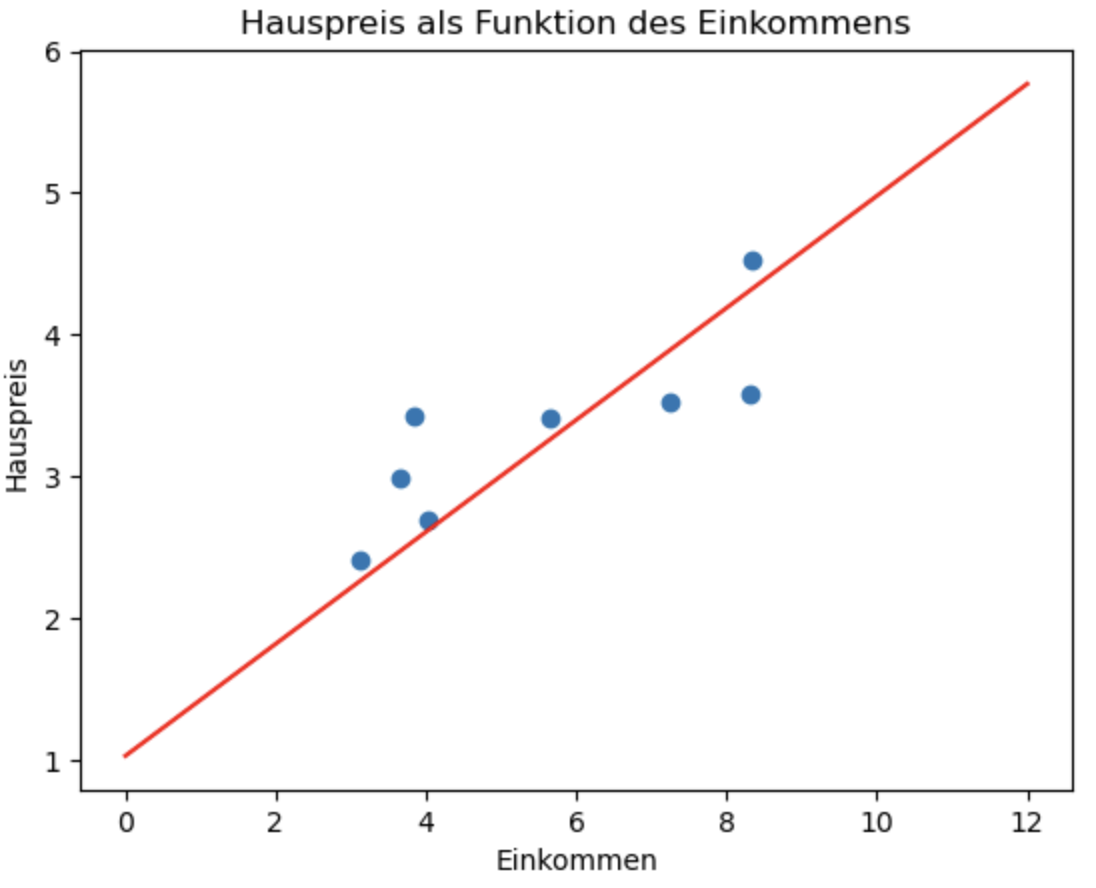
Man nennt diese Gerade auch die Regressionsgerade.
2.2.3 Lösung durch Optimierung
Wir suchen die optimalen Werte \(w\). Was optimal genau bedeutet, legen wir über eine Zielfunktion fest, engl. objective function. Diese spiegelt entweder Fehler oder Kosten wider und muss dann minimiert werden, dann spricht man von einer Verlust- oder Fehlerfunktion, engl. loss function. Alternativ kann sie auch Nutzen oder den Gewinn angeben, dann muss sie maximiert werden. Eine solche Funktion nennt man Nutzenfunktion, engl. utility function. Beide Spielarten sind klassische Probleme der mathematischen Optimierung.
Wir messen den Fehler als Differenz zwischen der Anwendung unseres Modells \(h_w\) auf einen Input \(x\) und dem entsprechenden Zielwert \(y\) aus den Trainingsdaten (siehe Abbildung 2.3).
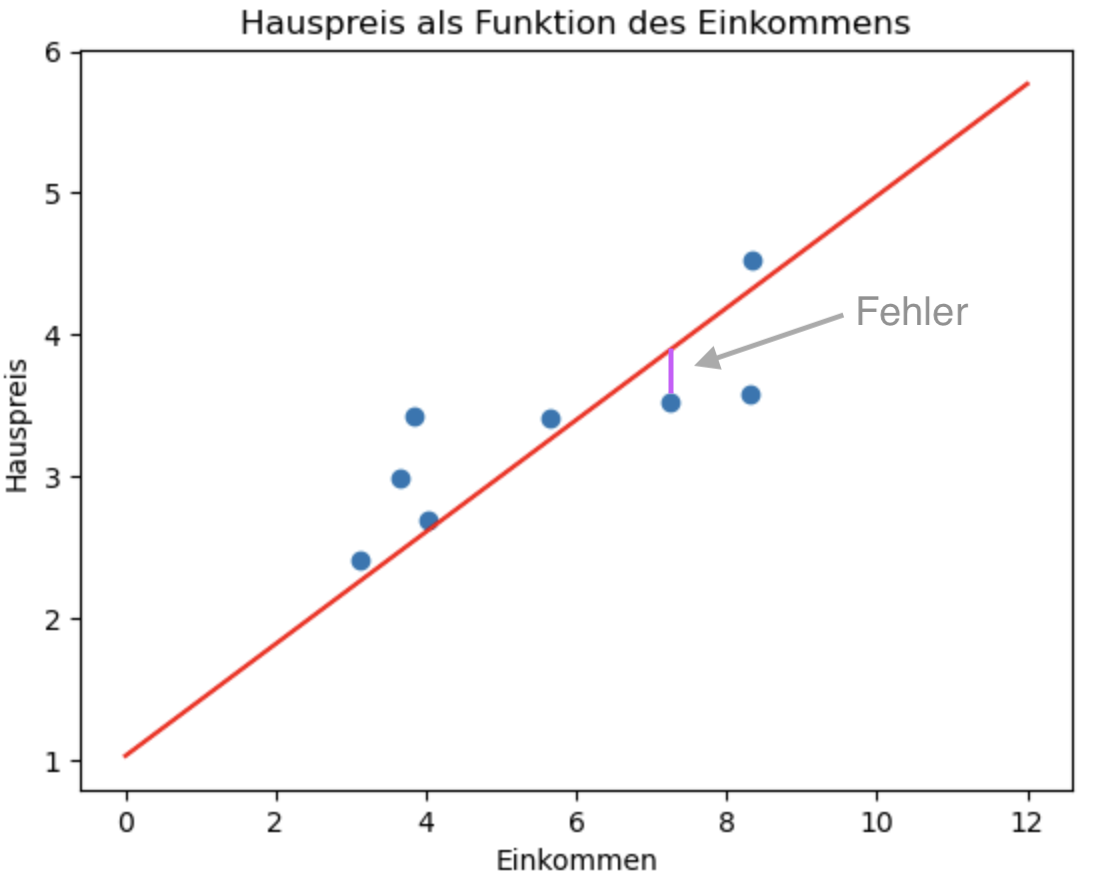
Zur Erinnerung: Unsere Trainingsdaten bestehen aus \(N\) Tupeln der Form \((x^k, y^k)\). Genauer gesagt nehmen wir die Summe der quadratischen Fehler, teilen diese durch die Anzahl der Trainingsbeispiele und erhalten so den mittleren quadratischen Fehler, engl. mean squared error oder MSE:
\[ \frac{1}{N} \sum_{k=1}^N \left( y^k - h_w (x^k) \right)^2 \]
Warum wird das Quadrat genommen und nicht der Betrag? Weil die Quadratsfunktion differenzierbar ist, d.h. man kann die Ableitung bilden, um ein Verfahren namens Gradientenabstieg, engl. gradient descent, einzusetzen.
Die Betragsfunktion ist hingegen nicht differenzierbar, da sie nicht-stetig am Nullpunkt ist (auch gut erklärt bei Wikipedia unter Differenzierbarkeit).
Wir zeigen hier nochmal die beiden Funktionen um den Nullpunkt herum.
Betragsfunktion
x = np.arange(-10, 10, .1) # stellt eine Reihe von Werten von -10 bis 10 mit Schrittweite 0.1 als Numpy-Array her
y = abs(x) # wendet die Funktion elementweise auf die Werte an und produziert einen neuen Numpy-Array
plt.plot(x,y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Betragsfunktion')
plt.xticks([-10,-5,0,5,10])
plt.yticks([0,5, 10])
plt.show()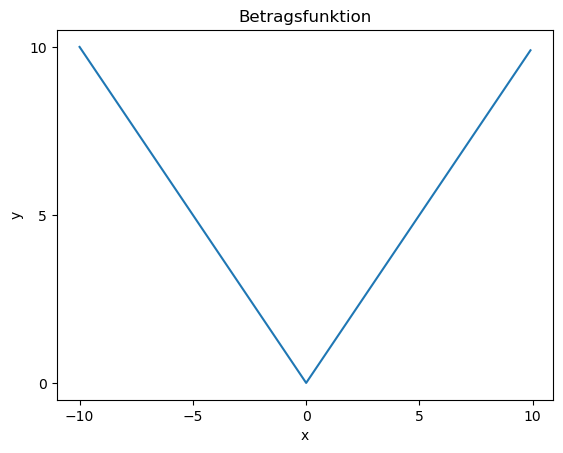
Sie sehen, dass die Betragsfunktion am Nullpunkt nicht differenzierbar ist. Was heißt differenzierbar überhaupt? Damit eine Funktion differenzierbar ist, muss man eine Tangente an jedem Punkt bestimmen können. Wenn Sie eine “Ecke” sehen, ist das nicht möglich.
x = np.arange(-10, 10, .1) # stellt eine Reihe von Werten von -10 bis 10 mit Schrittweite 0.1 als Numpy-Array her
y = x**2 # Schreibweise für Potenz
plt.plot(x,y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Quadratfunktion')
plt.xticks([-10,-5,0,5,10])
plt.yticks([0,50, 100])
plt.show()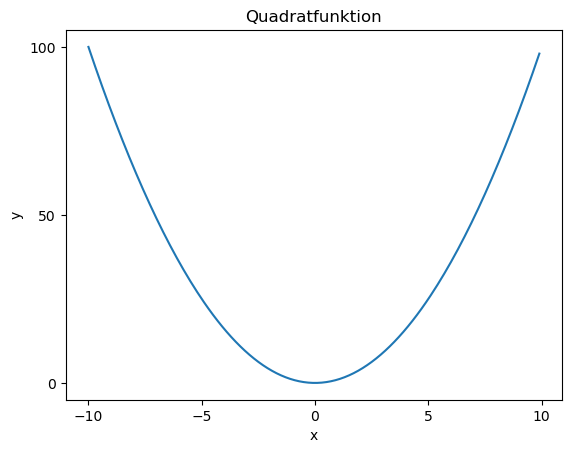
Bei der Quadratfunktion gibt es eine Tangente am Nullpunkt, diese hätte die Steigung 0. Es lässt sich also zu \(f(x) = x^2\) die Ableitung bilden, nämlich \(f'(x) = 2x\).
Dass eine Funktion nicht differenzierbar ist, ist kein “Knock-out-Kriterium”, wenn es um Gradientenabstieg geht. Es erleichtert aber die mathematischen Herleitungen, da man sonst Fallunterscheidungen einführen müsste. Im Bereich Neuronaler Netze, wo auch Gradientenabstieg verwendet wird, wird z.B. aktuell häufig die sogenannte ReLU-Funktion benutzt, die nicht-differenzierbar bei \(x=0\) ist.
Als nächstes sehen wir uns ein Verfahren an, mit dem wir Parameter für ein Modell finden, das die Zielfunktion optimiert.
2.2.4 Gradientenabstieg
Eine Umsetzung von Optimierung kann durch ein Verfahren namens Gradientenabstieg (engl. gradient descent) geleistet werden. Im Anschluss illustrieren einfache lineare Regression mit einem konkreten Beispiel in Python in Abschnitt 2.3.
Modell
Als nächstes bilden wir ein Modell und versuchen dieses dann anhand der Daten in der Tabelle zu optimieren.
Das Modell für eine lineare Regression ist eine lineare Funktion \(h\). Bei der einfachen linearen Regression hat \(h\) die Form:
\[ h(x) = w_0 + w_1 x \]
wobei hier \(w_0\) und \(w_1\) Skalare sind. Die Funktion repräsentiert also eine Gerade mit Steigung \(w_1\) und y-Achsenabschnitt \(w_0\).
Unsere Beispieldaten schreiben wir in der Form \((x^k, y^k)\), wobei \(x^k\) das jeweilige Einkommen der Gegend darstellt und \(y^k\) den Hauspreis. Index \(k\) repräsentiert die Zeile in unserer Datentabelle. Wenn \(N\) die Gesamtzahl der Daten (=Zeilen) bezeichnet, läuft Index \(k\) also von \(1\) bis \(N\). Man schreibt auch \(k \in {1, \ldots, N}\).
Zielfunktion
Wir definieren unsere Ziel- bzw. Fehlerfunktion \(J\) wie oben beschrieben als mittleren quadratischen Fehler (MSE). Jeder Fehler ist die quadrierte Differenz zwischen dem tatsächlichen Wert \(y^k\) und dem errechneten Wert unseres Modells \(h(x^k)\).
\[\begin{align*} \tag{ziel} J :&= \frac{1}{N} \sum_{k=1}^N \left( y^k - h(x^k) \right)^2 \\[2mm] &= \frac{1}{N} \sum_{k=1}^N \left( y^k - (w_0 + w_1 x^k) \right)^2 \end{align*}\]
Man sollte sich bewusst machen, dass die Zielfunktion alle Trainingsbeispiele umfasst, es ist also eine sehr, sehr lange Summe:
\[ J = \frac{1}{N} \left[ \left( y^1 - h(x^1) \right)^2 + \left( y^2 - h(x^2) \right)^2 + \ldots + \left( y^N - h(x^N) \right)^2 \right] \]
Man bedenke außerdem, dass in dem \(h\) die beiden Parameter \(w_0\) und \(w_1\) stecken:
\[ J = \frac{1}{N} \left[ \left( y^1 - (w_0 + w_1 x^1) \right)^2 + \left( y^2 - (w_0 + w_1 x^2) \right)^2 + \ldots + \left( y^N - (w_0 + w_1 x^N) \right)^2 \right] \]
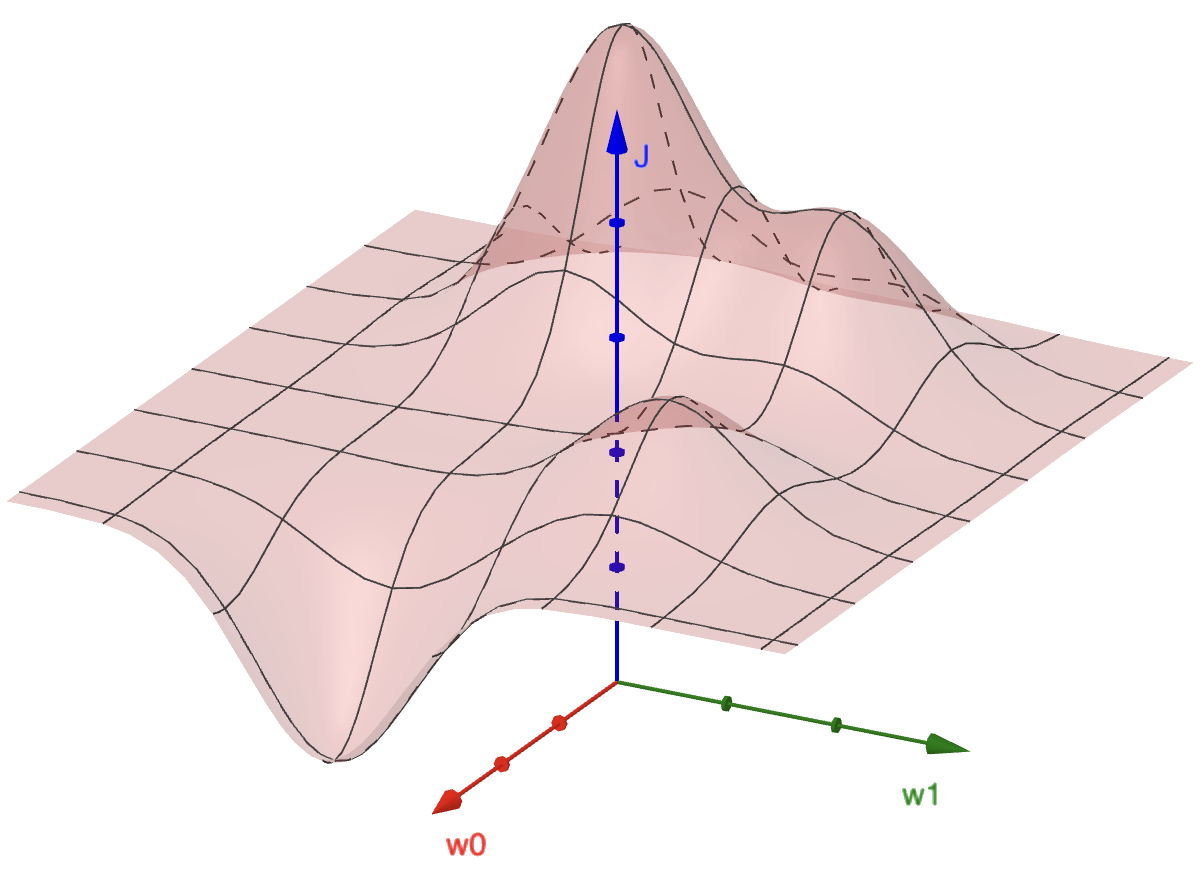
Man kann sich die Beziehung zwischen den beiden Parametern \(w_0\) und \(w_1\) und dem Fehler \(J\) als 3D-Landschaft vorstellen wie in Abbildung 2.4. Je nachdem, welche Werte wir für \(w_0\) und \(w_1\) wählen, sind wir in dieser Landschaft höher (= großer Fehler) oder tiefer (= niedriger Fehler). Da wir einen möglichst kleinen Fehler erzielen möchten, suchen wir die Parameter \(w_0\) und \(w_1\), die im tiefsten Tal dieser Landschaft liegen.
Gradient
Unser Modell zu optimieren bedeutet, die Parameter \((w_0, w_1)\) schrittweise anzupassen, so dass der Fehler \(J\) immer kleiner wird. Dazu müssen wir wissen, wie wir \((w_0, w_1)\) genau anpassen müssen. Der Gradient an einem bestimmten Punkt \((w_0, w_1)\) in dieser Fehlerlandschaft ist ein Vektor, der in Richtung der höchsten Steigung zeigt. Wir nehmen also den umgekehrten Gradienten, um schrittweise in Richtung des geringsten \(J\) zu gehen (siehe Abbildung 2.5). Das nennt man Gradientenabstieg.
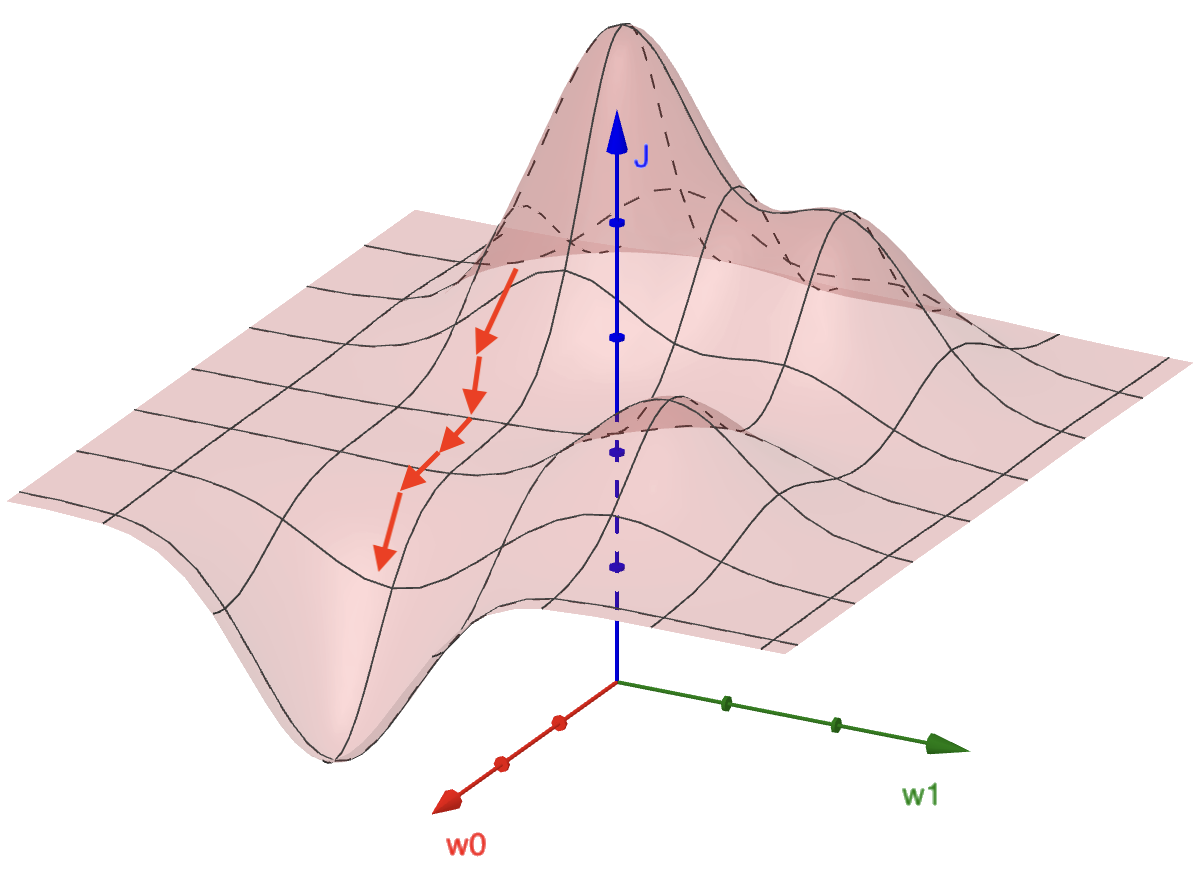
Der Gradient ist ein Vektor mit zwei Komponenten. Die Idee ist, dass wir sowohl in Richtung \(w_0\) als auch in Richtung \(w_1\) die Steigung berechnen und beides in einen Vektor packen. Konkret berechnen wir für jeden Parameter die partielle Ableitung. Bei der Berechnung kommt die Kettenregel zum Einsatz.
\[\begin{align*} \frac{\partial J}{\partial w_0} & = \frac{1}{N} \sum_{k=1}^N - 2\left( y^k - (w_0 + w_1 x^k) \right) \\[2mm] \frac{\partial J}{\partial w_1} & = \frac{1}{N} \sum_{k=1}^N - 2x^k\left( y^k - (w_0 + w_1 x^k) \right) \end{align*}\]
Jetzt setzen wir wieder \(h(x^k)\) ein:
\[\begin{align*}\tag{grad} \frac{\partial J}{\partial w_0} & = \frac{1}{N} \sum_{k=1}^N - 2\left( y^k - h(x^k) \right) \\[2mm] \frac{\partial J}{\partial w_1} & = \frac{1}{N} \sum_{k=1}^N - 2x^k\left( y^k - h(x^k) \right) \end{align*}\]
Beachten Sie, dass aufgrund der Summierung alle Trainingsbeispiele zur Berechnung dieser Ableitungen durchlaufen werden müssen. Bei der Implementation werden wir dies in einer Schleife tun.
Training
Das Training führt jetzt die Optimierung durch. Das Ziel ist, durch schrittweise Anpassung - also Updates der Parameter - die optimalen Werte für \(w_0\) und \(w_1\) zu finden. Zu Beginn initialisieren wir die Parameter wie folgt:
\[\begin{align*} w_0 & := 0\\[2mm] w_1 & := 0 \end{align*}\]
Das Training vollzieht sich in Runden, die wir Epochen nennen.
Das Update der Parameter \(w_0\) und \(w_1\) geschieht mit Hilfe der jeweiligen partiellen Ableitung:
\[\begin{align*}\tag{update} w_0 & := w_0 - \alpha \frac{\partial J}{\partial w_0}\\[2mm] w_1 & := w_1 - \alpha \frac{\partial J}{\partial w_1} \end{align*}\]
Um die obigen Ableitungen zu berechnen, müssen alle Trainingsbeispiele durchlaufen werden; das sieht man am Summenzeichen in Gleichung (grad). Daher kann erst am Ende der Epoche das Update der Parameter durchgeführt werden.
Im Bereich des maschinellen Lernens bedeutet eine Epoche im Training, dass der komplette Trainingsdatensatz (also alle Trainingsbeispiele) einmal durchlaufen wird. Wieviele Updates pro Epoche durchgeführt werden, hängt vom Lernverfahren ab. In unserem Fall wird pro Epoche ein Update der Parameter durchgeführt.
Da die Ableitungen in eine Richtung zeigen, die den Fehler \(J\) vergrößern, müssen wir die Ableitungen im Update-Schritt negieren, denn wir wollen ja den Fehler verringern. Daher das Minuszeichen.
Außerdem möchten wir kontrollieren, wie stark wir die Parameter pro Update ändern - manchmal nennt man das die Schrittweite. Das wird über die Lernrate \(\alpha\) gesteuert, ein Wert \(\in (0, 1)\), der als Faktor die Ableitung modifiziert. Je höher \(\alpha\) ist, umso schneller wird gelernt. Ein zu hoher Wert birgt aber die Gefahr, ein Minimum zu überspringen und im schlimmsten Fall um das Minimum herum zu oszillieren.
Für die Wahl der Lernrate gibt es keine allgemeingültige Empfehlung, in der Praxis zeigt sich aber, dass Werte um \(0.1\) bis \(0.3\) gute Ausgangspunkte sind. Teilweise kann die Lernrate aber auch deutlich niedriger ausfallen; wir verwenden später zum Beispiel \(\alpha = 0.001\). Die Lernrate wird im einfachsten Fall empirisch festgestellt.
Empirisch heißt “aus Erfahrung”, d.h. etwas basiert auf Beobachtungen.
Hyperparameter
Die Lernrate ist ein Beispiel für einen Hyperparameter. Ein Hyperparameter ist ein Parameter, der während des Trainings nicht verändert wird, wohingegen unsere “normalen” Parameter \(w_0\) und \(w_1\) ja während des Trainings fortlaufend angepasst werden.
Ein weiteres Bespiel für einen Hyperparameter ist die Trainingsdauer, also die Anzahl der Epochen, mit der ein Netz trainiert wird. Entgegen der ersten Intuition ist es nicht immer gut, ein Modell möglich lang zu trainieren, denn dann kann es zu Overfitting kommen (siehe Abschnitt 2.4).
Trainingsprozess
Abbildung 2.6 zeigt den Trainingsprozess schematisch. Pro Epoche wird ein Update der Parameter \(w_0\) und \(w_1\) mit Hilfe der partiellen Ableitungen durchgeführt. Diese Ableitungen nennt man auch den Gradienten. Für die Berechnung werden innerhalb einer Epoche alle \(N\) Trainingsdaten durchlaufen und der jeweilige Summand für die Ableitungen aufgesammelt. Am Ende jeder Epoche wird noch jeweils der Durchschnitt gebildet, dann hat man die Ableitungen und das Update der Parameter kann durchgeführt werden.
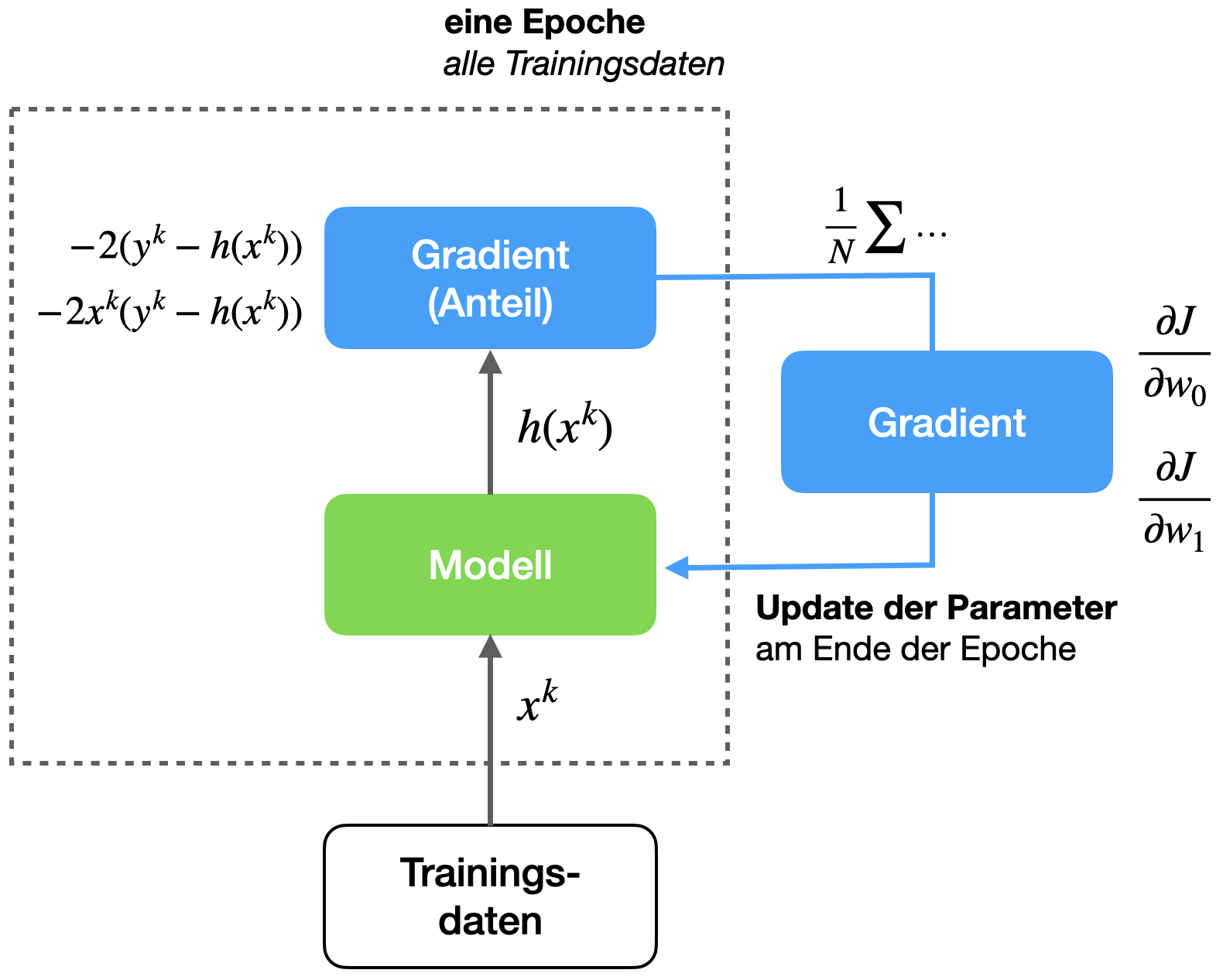
Im nächsten Abschnitt (2.3) sehen wir uns die Implementation des Verfahrens in Python an, damit Sie den Zusammenhang zwischen den Formeln und der Umsetzung sehen.
2.2.5 Erweiterte Regression
In den obigen Versuchen haben wir mit einer einfachen linearen Funktion gearbeitet, die zwei Parameter hat (\(w_0\) und \(w_1\)), die einen einfachen Inputwert \(x\) hat und einen einfachen Outputwert \(y = h(x)\).
\[ h(x) = w_0 + w_1 x \]
Polynomiale Regression
Natürlich könnte man noch höhere Potenzen von x hinzunehmen, um so eine Kurve zu erzeugen, die sich den Daten besser anschmiegt. Nehmen wir \(x^2\) dazu, spricht man von quadratischer Regression:
\[ h(x) = w_0 + w_1 x + w_2 x^2 \]
In diesem Fall erhalten wir keine Regressionsgerade, sondern eine U-förmige Kurve (Parabel). Entsprechend bekommen Sie komplexere Kurven mit steigender Zahl von Potenzen:
\[\begin{align*} h(x) & = w_0 + w_1 x + w_2 x^2 \\[1mm] h(x) & = w_0 + w_1 x + w_2 x^2 + w_3 x^3 \\[1mm] & \vdots\\[1mm] h(x) & = w_0 + w_1 x + \ldots + w_n x^n \end{align*}\]
Beachten Sie aber, dass die Parameter \(w_0, w_1, \ldots\) immer noch linear sind (also nicht z.B. zu einer Potenz erhoben werden). Das Verfahren ist tatsächlich immer noch sehr einfach.
Multiple lineare Regression
In der Regel haben Sie natürlich nicht nur ein Input-Feature wie mittleres Einkommen im Hausbeispiel. Sie haben z.B. noch Anzahl der Zimmer, Größe in qm, Alter in Jahren etc. Jedes Feature wird mit einer weiteren Input-Variablen \(x_1\), \(x_2\) usw. erfasst, so dass man insgesamt einen Vektor \(x = (x_1, x_2, \ldots, x_n)\) hat.
Unsere Formel für das Modell sieht dann z.B. so aus
\[ h(x) = w_0 + w_1 x_1 + w_2 x_2 + \ldots + w_n x_n \]
Auch hier ist es relativ leicht, das Verfahren entsprechend anzupassen.
2.3 Lineare Regression implementieren
Wir sehen uns an, wie wir die gelernten Methoden in Python umsetzen. Dazu müssen wir uns zunächst Daten beschaffen.
2.3.1 Daten: California housing dataset
Für unser Python-Beispiel schauen wir hier den Datensatz California housing dataset. In diesem Datensatz ist der Kaufpreis von Häusern in Kalifornien erfasst, zusammen mit verschiedenen Features, z.B. dem Alter des Hauses, die Anzahl der Zimmer oder auch das Durchschnittseinkommen der Gegend, in der das Haus steht. Die Idee ist, den Hauspreis für ein “neues” Haus vorherzusagen, wenn man die entsprechenden Features kennt. Wir werden uns das Feature Durchschnittseinkommen herauspicken, so dass wir einfache Datenpaare \((x^k, y^k)\), wo das \(x^k\) ein solcher Einkommenswert ist und das \(y^k\) der Kaufpreis eines Hauses.
Dieser Datensatz ist in der Bibliothek Scikit-learn enthalten, d.h. wir können ihn mit einer Anweisung in den Speicher laden. Siehe auch ein schöne Darstellung des Datensatzes vom Inria Learning Lab.
Wir packen die Daten in einen Pandas-Dataframe (daher df). Ein Pandas-Dataframe ist einfach eine Tabelle. Eine Tabelle ist eine Matrix, die zusätzlich Zeilen- und Spaltenbeschriftungen hat:
# Für dieses Beispiel wird das Paket scikit-learn benötigt
from sklearn.datasets import fetch_california_housing
housing = fetch_california_housing()
df = pd.DataFrame(data=housing.data, columns=housing.feature_names)Pandas ist eine Python-Bibliothek, die im Bereich Data Science bzw. Machine Learning sehr wichtig ist zur Verwaltung, Aufbereitung und Analyse von Daten. Der Name “Pandas” kommt von “panel data”. Das wichtigste Feature von Pandas ist die Verwaltung von Daten in Tabellen (mit entsprechenden Beschriftungen für Zeilen und Spalten), die in Pandas Dataframes heißen. Pandas baut auf NumPy auf.
Wir greifen in unserem Kontext nur ab und zu auf Pandas zu, wenn Datensätze in Pandas vorliegen. Wir nutzen ansonsten praktisch keine Features von Pandas. Zur Datenmanipulation verwenden wir hauptsächlich NumPy.
Werfen wir einen Blick in die Tabelle. Die erste Spalte MedInc gibt den Median aller Einkommen der Gegend an, wo das Haus steht. Es erscheint plausibel, dass das ein guter Wert ist, um den Wert des Hauses einzuschätzen. Die Vermutung wäre: Je höher das Einkommen, desto höher die Hauspreise. Wir überprüfen diese Hypothese im Folgenden.
df.head(5) # zeigt die ersten 5 Zeilen der Tabelle| MedInc | HouseAge | AveRooms | AveBedrms | Population | AveOccup | Latitude | Longitude | |
|---|---|---|---|---|---|---|---|---|
| 0 | 8.3252 | 41.0 | 6.984127 | 1.023810 | 322.0 | 2.555556 | 37.88 | -122.23 |
| 1 | 8.3014 | 21.0 | 6.238137 | 0.971880 | 2401.0 | 2.109842 | 37.86 | -122.22 |
| 2 | 7.2574 | 52.0 | 8.288136 | 1.073446 | 496.0 | 2.802260 | 37.85 | -122.24 |
| 3 | 5.6431 | 52.0 | 5.817352 | 1.073059 | 558.0 | 2.547945 | 37.85 | -122.25 |
| 4 | 3.8462 | 52.0 | 6.281853 | 1.081081 | 565.0 | 2.181467 | 37.85 | -122.25 |
Wir speichern uns die erste Spalte mit dem Median der Einkommen:
incomes = df['MedInc'].array
incomes<PandasArray>
[8.3252, 8.3014, 7.2574, 5.6431, 3.8462, 4.0368, 3.6591, 3.12, 2.0804,
3.6912,
...
3.5673, 3.5179, 3.125, 2.5495, 3.7125, 1.5603, 2.5568, 1.7, 1.8672,
2.3886]
Length: 20640, dtype: float64Unsere Zielwerte - die Preise der Häuser - sind nicht in der Tabelle, sondern stecken noch in der Datenstruktur housing:
prices = housing.target
pricesarray([4.526, 3.585, 3.521, ..., 0.923, 0.847, 0.894])Die Hauspreise sind in 100000 USD angegeben. Das erste Haus kostet also etwa 450000 USD.
Kurzer “Sanity check”: Wie lang sind die Arrays und sind sie gleich lang?
print(len(prices), len(incomes))20640 20640Da das doch sehr viele Werte sind, beschränken wir uns auf die ersten 200 Werte. Sonst werden die Plots unten zu unübersichtlich.
prices = prices[:200]
incomes = incomes[:200]
len(prices)200Visualisierung der Daten
Wir sehen uns die Verteilung der Datenpunkte an: Auf der y-Achse sind die Hauspreise verzeichnet, auf der x-Achse die Einkommen. Diese Plots nennt man auch Scatterplots, weil man dort die Verteilung der einzelnen Datenpunkte gut sehen kann.
Hier zeigt sich klar, dass es eine Korrelation zu geben scheint: Je höher das Einkommen, umso höher der Hauspreis.
plt.scatter(incomes, prices)
plt.ylabel('Hauspreis')
plt.xlabel('Einkommen')
plt.title('Hauspreise als Funktion des Einkommens')
plt.show()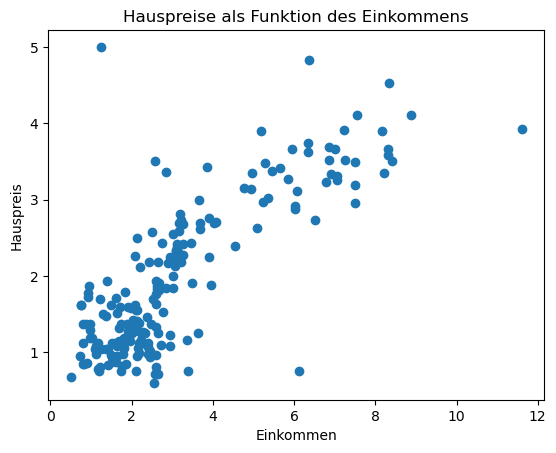
2.3.2 Umsetzung in Python
Zunächst sehen wir uns an, wie man lineare Regression von Grund auf in Python implementiert. Oft versteht man so am besten, wie die Theorie in die Praxis übertragen wird.
Ganz grob betrachtet müssen wir Folgendes tun:
Für jede Epoche:
Berechne die partiellen Ableitungen wie in (grad)
Führe ein Update der Parameter durch gemäß (update)Berechnung der Ableitung und Update
Wir schreiben eine Funktion update, die für jede Epoche aufgerufen wird. Die Funktion bekommt die aktuellen Werte der Parameter \(w_0\) und \(w_1\) und gibt die ge-updateten Werte zurück. Außerdem bekommt die Funktion noch die Traningsdaten übergeben (zwei Vektoren x und y) sowie die Lernrate alpha.
Um das Update durchzuführen müssen wir die zwei partiellen Ableitungen berechnen. Zur Erinnerung:
\[\begin{align*} \frac{\partial J}{\partial w_0} & = \frac{1}{N} \sum_{k=1}^N - 2\left( y^k - (w_0 + w_1 x^k) \right) \\[2mm] \frac{\partial J}{\partial w_1} & = \frac{1}{N} \sum_{k=1}^N - 2x^k\left( y^k - (w_0 + w_1 x^k) \right) \end{align*}\]
Sie sehen im Code unten, dass wir in einer Schleife alle Trainingsbeispiele durchlaufen, um die Summe zu berechnen. Wir speichern die (Zwischen-)Werte in den Variablen dJw0 und dJw1. Erst beim Update wird das \(1/N\) durchgeführt. Dies entspricht einer Epoche.
# Eingabe: Trainingsdaten, die beiden Parameter und Lernrate
def update(x, y, w1, w0, alpha):
# Schritt 1: Ableitungen berechnen
dJdw1 = 0
dJdw0 = 0
N = len(x)
for i in range(N):
dJdw1 += -2 * x[i] * (y[i] - (w1 * x[i] + w0))
dJdw0 += -2 * (y[i] - (w1 * x[i] + w0))
# Schritt 2: Updates durchführen
w1 = w1 - (1/float(N)) * dJdw1 * alpha
w0 = w0 - (1/float(N)) * dJdw0 * alpha
return w1, w0Trainingsfunktion
Jetzt definieren wir die Funktion train, die das Training in mehreren Epochen durchführt.
Wir speichern in jeder Epoche den Fehlerwert (Loss) und die Parameterwerte in einer Liste, der Historie. Außerdem geben wir alle 100 Epochen den Zwischenstand auf der Konsole aus. Das History-Objekt geben wir am Ende des Funktionscodes zurück.
# Eingabe: x-Werte, y-Werte, Parameter, Lernrate und Anzahl der Epochen
def train(x, y, w1, w0, alpha, epochs):
history = []
for e in range(epochs):
# Historie speichern
l = loss(x, y, w1, w0)
history.append((l, w1, w0))
if e % 100 == 0:
print(f"epoch: {e:4} loss: {l:7.3f} w1={w1:.3f} w0={w0:.3f}")
w1, w0 = update(x, y, w1, w0, alpha)
return historyFehlerfunktion
Es fehlt noch die oben verwendete Funktion loss, die den aktuellen Fehler (MSE) gemäß Formel (ziel) berechnet. Auch hier müssen alle Trainingsbeispiele in einer Schleife durchlaufen werden.
In Python bedeutet der Doppelstern “potenzieren”, d.h. für “x hoch 2” schreibt man in Python: x**2
# Eingabe: x-Werte, y-Werte und Parameter
def loss(x, y, w1, w0):
N = len(x)
error = 0
# summiere quadratischen Fehler auf
for i in range(N):
error += (y[i] - (w1 * x[i] + w0))**2
# gib Mittelwert zurück
return error / float(N)Training
Jetzt können wir trainieren. Wir initialisieren unsere Parameter mit 0 und wählen eine sehr niedrige Lernrate von 0.001. Es sollen 3000 Epochen durchlaufen werden. Wir speichern die zurückgegebene Historie.
history = train(incomes, prices, 0, 0, .001, 3000)epoch: 0 loss: 4.833 w1=0.000 w0=0.000
epoch: 100 loss: 0.481 w1=0.493 w0=0.149
epoch: 200 loss: 0.459 w1=0.510 w0=0.187
epoch: 300 loss: 0.448 w1=0.504 w0=0.219
epoch: 400 loss: 0.439 w1=0.498 w0=0.249
epoch: 500 loss: 0.431 w1=0.491 w0=0.276
epoch: 600 loss: 0.424 w1=0.485 w0=0.303
epoch: 700 loss: 0.417 w1=0.480 w0=0.328
epoch: 800 loss: 0.411 w1=0.474 w0=0.351
epoch: 900 loss: 0.406 w1=0.469 w0=0.373
epoch: 1000 loss: 0.402 w1=0.465 w0=0.394
epoch: 1100 loss: 0.397 w1=0.460 w0=0.414
epoch: 1200 loss: 0.394 w1=0.456 w0=0.433
epoch: 1300 loss: 0.391 w1=0.452 w0=0.450
epoch: 1400 loss: 0.388 w1=0.448 w0=0.467
epoch: 1500 loss: 0.385 w1=0.445 w0=0.483
epoch: 1600 loss: 0.383 w1=0.441 w0=0.497
epoch: 1700 loss: 0.381 w1=0.438 w0=0.511
epoch: 1800 loss: 0.379 w1=0.435 w0=0.525
epoch: 1900 loss: 0.377 w1=0.432 w0=0.537
epoch: 2000 loss: 0.376 w1=0.430 w0=0.549
epoch: 2100 loss: 0.375 w1=0.427 w0=0.560
epoch: 2200 loss: 0.373 w1=0.425 w0=0.570
epoch: 2300 loss: 0.372 w1=0.423 w0=0.580
epoch: 2400 loss: 0.371 w1=0.420 w0=0.590
epoch: 2500 loss: 0.371 w1=0.418 w0=0.598
epoch: 2600 loss: 0.370 w1=0.417 w0=0.607
epoch: 2700 loss: 0.369 w1=0.415 w0=0.615
epoch: 2800 loss: 0.369 w1=0.413 w0=0.622
epoch: 2900 loss: 0.368 w1=0.412 w0=0.629Sanity check: Wir schauen uns die ersten 5 Einträge der Historie an. Jeder Eintrag sollte ein 3-Tupel mit Loss, w1 und w0 enthalten.
history[:5][(4.8325005300005, 0, 0),
(4.576862434147349, 0.015626331876340004, 0.003914440100000001),
(4.3362345247875265, 0.030784316641758333, 0.00772275025382289),
(4.109734998459303, 0.0454879210288684, 0.011428088967518804),
(3.896533855539058, 0.05975069530422363, 0.015033520569153993)]Visualisierung
Wir können die Plotfunktion der Matplotlib-Bibliothek nutzen, um die Fehlerentwicklung über die Epochen zu visualisieren.
Dazu benötigen wir eine Liste der Loss-Werte. Wir wenden List Comprehension an.
losses = [x[0] for x in history]
losses[:5] # Sanity check[4.8325005300005,
4.576862434147349,
4.3362345247875265,
4.109734998459303,
3.896533855539058]Jetzt der Plot. Die Plotfunktion benötigt für die Werte zwei Listen, eine für die x-Werte, eine für die y-Werte.
Für die x-Achse erzeugen wir eine einfache Liste der Form (1, 2, …, 30).
plt.plot(range(len(losses)), losses, label='Loss-Entwiclung')
plt.ylabel("Loss")
plt.xlabel("Epochen")
plt.show()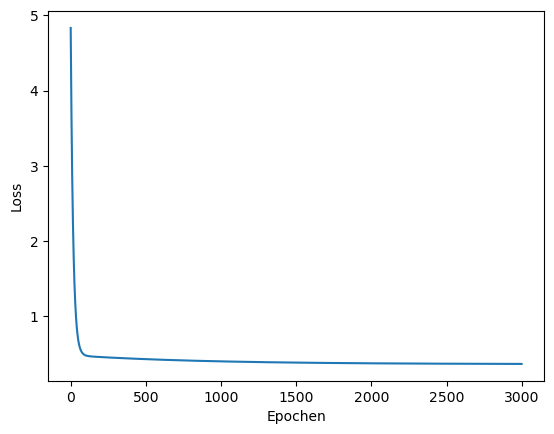
Finale (optimale) Parameterwerte
Der letzte Eintrag der Historie enthält hier die optimalen Parameterwerte, die wir zwischenspeichern.
last = history[len(history)-1]
w1opt = last[1]
w0opt = last[2]
print(f'w1 = {w1opt:.3f} w0 = {w0opt:.3f}')w1 = 0.410 w0 = 0.635Vorhersagen
Jetzt kann man die berechneten Parameter \(w_0\) und \(w_1\) verwenden, um Vorhersagen zu treffen. Wir möchten wissen, welche Verkaufszahl zu erwarten ist, wenn wir einen bestimmten Betrag für Werbung ausgeben.
Dazu definieren wir die Funktion predict, die einfach die Funktion \(h\) auf einem beliebigen \(x\) mit den angegebenen Parametern anwendet.
def predict(x, w1, w0):
return w1*x + w0Wir fragen uns, was in einer Gegend mit einem Median-Einkommen von 10 für ein Hauspreis zu erwarten ist. Oben hat unser Algorithmus die optimalen Parameter berechnet, die wir jetzt in unsere Vorhersagefunktion einsetzen:
predict(10, w1opt, w0opt)4.735790571398752Schauen Sie oben im Scatterplot bei 10 (auf der x-Achse) nach, ob die Vorsage plausibel ist.
Visualisierung der Regressionsgeraden
Jetzt schauen wir uns nochmal den Scatterplot von oben an und zeichnen die Gerade ein, die sich aus den berechneten Parametern ergibt. Dazu zeichnen wir eine Linie von x=0 bis x=50 und berechnen die y-Werte mit Hilfe unserer Funktion predict.
Das tun wir in folgender Funktion:
def plot_scatter_regress(w1, w0, title):
plt.scatter(incomes, prices)
plt.plot([0, 12], [predict(0, w1, w0), predict(12, w1, w0)], 'r-') # Regressionsgerade
plt.xlabel('Einkommen')
plt.ylabel('Hauspreis')
plt.title(title)
plt.show()Jetzt zeichnen wir Scatterplot und Regressionsgerade:
plot_scatter_regress(w1opt, w0opt, 'Hauspreis als Funktion des Einkommens')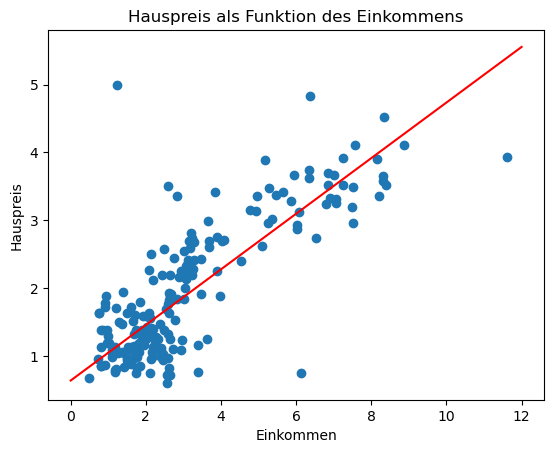
Visualisierung der Entwicklung
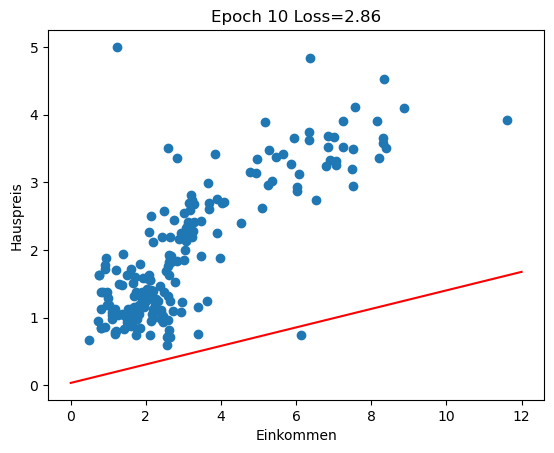
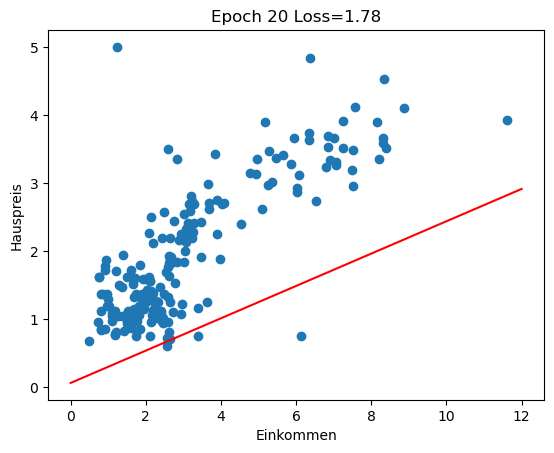
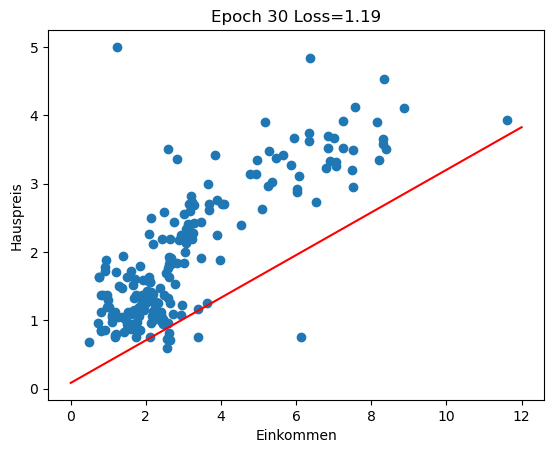
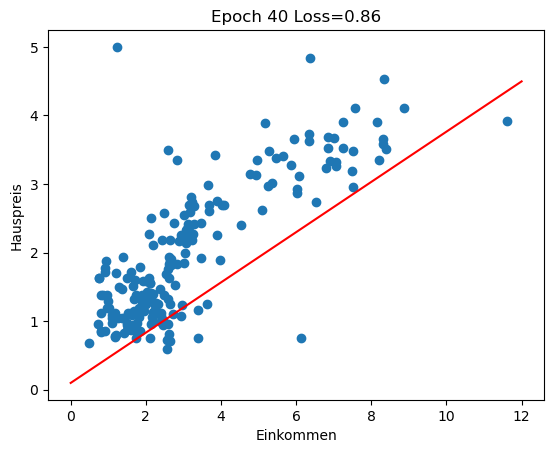
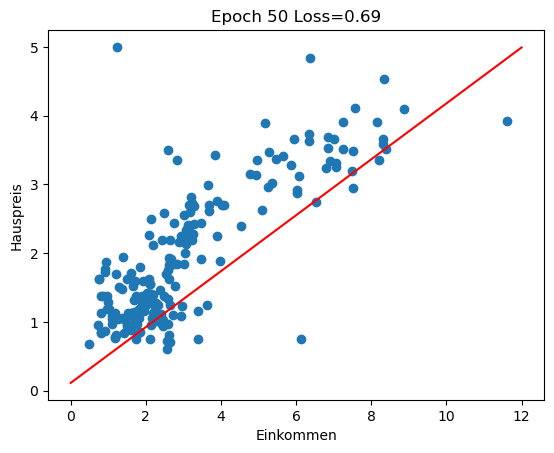
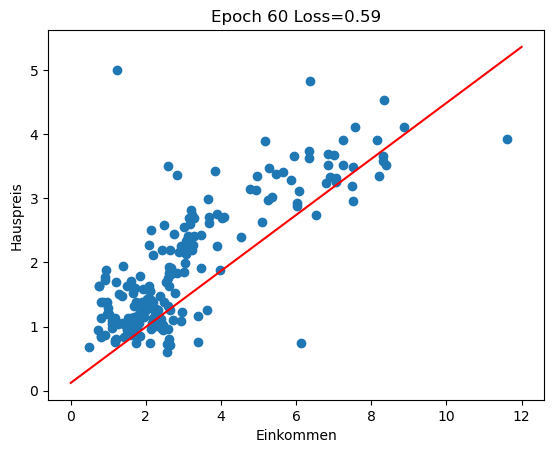
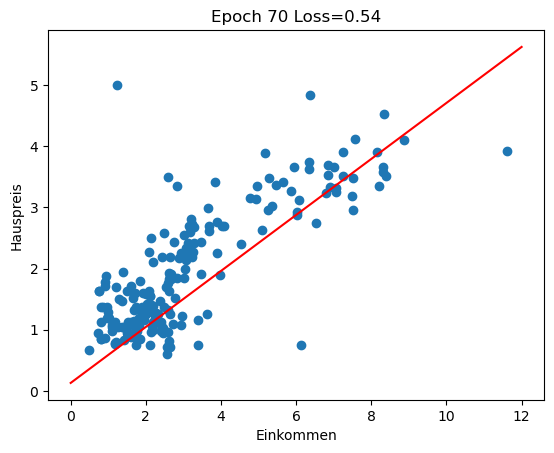
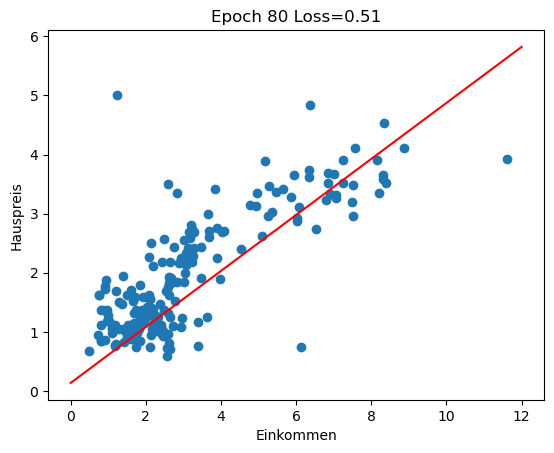
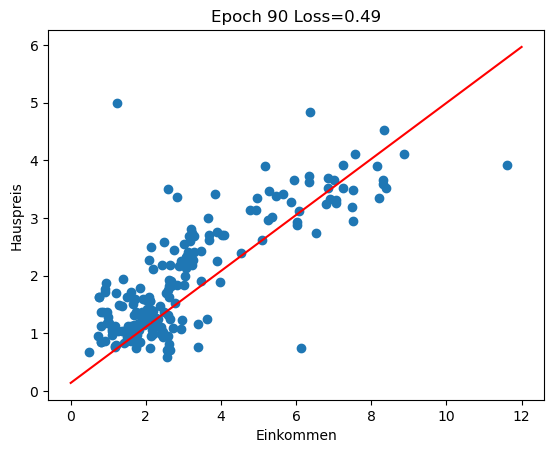
Im Rückblick schauen wir uns an, wie sich die Regressionsgerade in den ersten 100 Epochen des Trainings entwickelt (insgesamt 3000 Epochen). Man sieht gut, wie die Gerade zu Beginn große Sprünge macht und sich in späteren Epochen nur noch wenig verändert.
for i in range(0, 100, 10):
w1 = history[i][1]
w0 = history[i][2]
plot_scatter_regress(w1, w0, f'Epoch {i} Loss={history[i][0]:.2f}')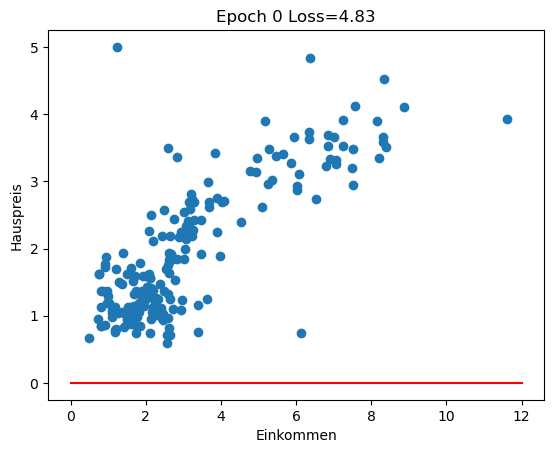
Varianten des Gradientenabstiegs
Unsere Variante des Gradientenabstiegs kann sehr langsam sein, insbesondere bei großen Datenmengen. Das liegt daran, dass wir in jeder Epoche erst durch alle Trainingsbeispiele durchlaufen, bevor wir die Parameter updaten. Ein weiterer Faktor ist die Lernrate \(\alpha\). Manchmal ist es gut, eine sehr niedrige Lernrate zu haben (in der Nähe des Minimums), manchmal ist eine höhere Lernrate besser, um schneller in die Nähe des Minimums zu kommen.
In den weiteren Kapiteln werden Sie Varianten wie stochastic gradient descent (SGD) und Minibatch kennen lernen. Außerdem werden wir bei den Neuronalen Netzen über Verfahren sprechen, die Lernrate adaptiv zu gestalten (Momentum, Adagrad, Adam …).
2.3.3 Umsetzung mit Scikit-learn
Oben haben wir lineare Regression selbst implementiert, aber natürlich gibt es das Verfahren schon in vielen Bibliotheken. Für die Praxis ist es nicht sinnvoll, eigene Implementierungen zu verwenden, da vorhandene Bibliotheken in der Regel von professionellen Entwicklern geschrieben und von vielen Experten auch im Praxiseinsatz getestet wurden, also deutlich zuverlässiger/robuster sind als Eigenentwicklungen.
Ein guter Grund, eigene Implementierungen vorzunehmen, ist allerdings der persönliche Lerneffekt. Oft versteht man ein Verfahren erst dann, wenn man es selbst implementiert hat. Ein weiterer Grund ist natürlich die Forschung, d.h. wenn man bekannte Verfahren modifizieren oder neue Verfahren entwickeln möchte.
Wir möchten jetzt statt der Eigenentwicklung oben eine erprobte Bibliothek nutzen. Wir verwenden die scikit-learn, eine Python-Bibliothek, die in den letzten Jahren zum Quasi-Standard für das Lernen und Entwickeln im Bereich Machine Learning geworden ist.
Daten
Wir nehmen uns die Einkommendaten und bilden sie zu einem 2-dimensionalen Array um, weil der Mechanismus von Scikit-learn die Eingabe in dieser Form benötigt. Grund: Es liegen in der Regel mehrere Eingabewerte pro Trainingsbeispiel vor.
Da die X-Werte 2-dimensional sind, schreibt man oft ein großes X, also X_train.
X_train = incomes.to_numpy() # Spalte zu NumPy-Array machen
X_train = X_train.reshape(-1, 1) # zu 2-dimensionalen Array umbilden (N Zeilen, 1 Spalte)
X_train[:5] # Testausgabe der ersten 5 Elementearray([[8.3252],
[8.3014],
[7.2574],
[5.6431],
[3.8462]])Die Zielwerte müssen in keine neue Form gebracht werden. Wir benennen sie lediglich um in y_train. Die Zielwerte sind ja ein 1-dimensionaler Array, daher ein kleines y.
y_train = prices
y_train[:5]array([4.526, 3.585, 3.521, 3.413, 3.422])Modell
Jetzt erstellen wir ein Modell, indem wir die Klasse LinearRegression instanziieren.
from sklearn.linear_model import LinearRegression
model = LinearRegression() # neues ModellTraining
Das Training wird in der Methode fit geleistet (“to fit” im Sinne von “anpassen”).
model.fit(X_train, y_train) # Training mit Eingabearray und ZielwertenLinearRegression()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LinearRegression()
Vorhersagen
Mit der Methode predict können wir jetzt Vorhersagen treffen. Oben hatten wir uns gefragt, welcher Hauspreis bei einem Median-Einkommen von 10 zu erwarten ist.
model.predict([[10]])array([4.59582307])Vergleichen Sie den Wert mit “unserem” Wert oben.
2.4 Overfitting und Traininigsdaten
2.4.1 Over- und Underfitting
Im Allgemeinen ist es so, dass eine hohe Anzahl von Parametern kombiniert mit langer Trainingsdauer zu einer genaueren Modellierung führt. Kann man dann sagen, dass das Modell immer besser wird? Wir sehen uns drei Modelle für dieselben Trainingsdaten an.
Underfitting
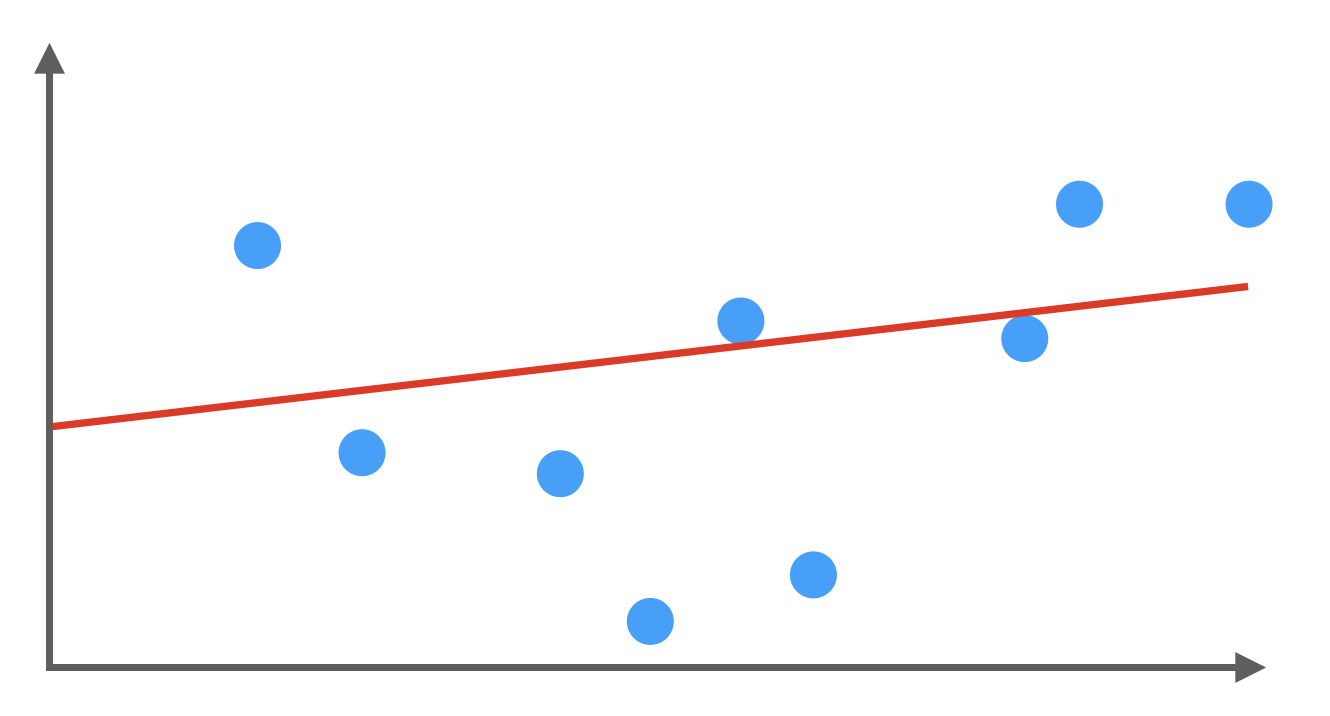
In der ersten Abbildung sehen wir das Ergebnis einer linearen Regression. Einige Datenpunkte werden sehr schlecht modelliert und wir sprechen daher von einem Underfitting. Das heißt, der Fehler, den das Modell bei Vorhersagen - selbst auf den Trainingsdaten - macht, ist relativ groß. Ganz grob kann man sagen, dass das Modell nicht komplex genug ist, was man an einer geringen Anzahl von Parametern erkennt. Zum Beispiel bei einem linearen Modell, das nur zwei Parameter \(w_0\) und \(w_1\) aufweist. Ein weiterer Grund könnte die geringe Aussagekraft der Eingabe-Features sein, dann müsste man die Auswahl der Features anpassen.
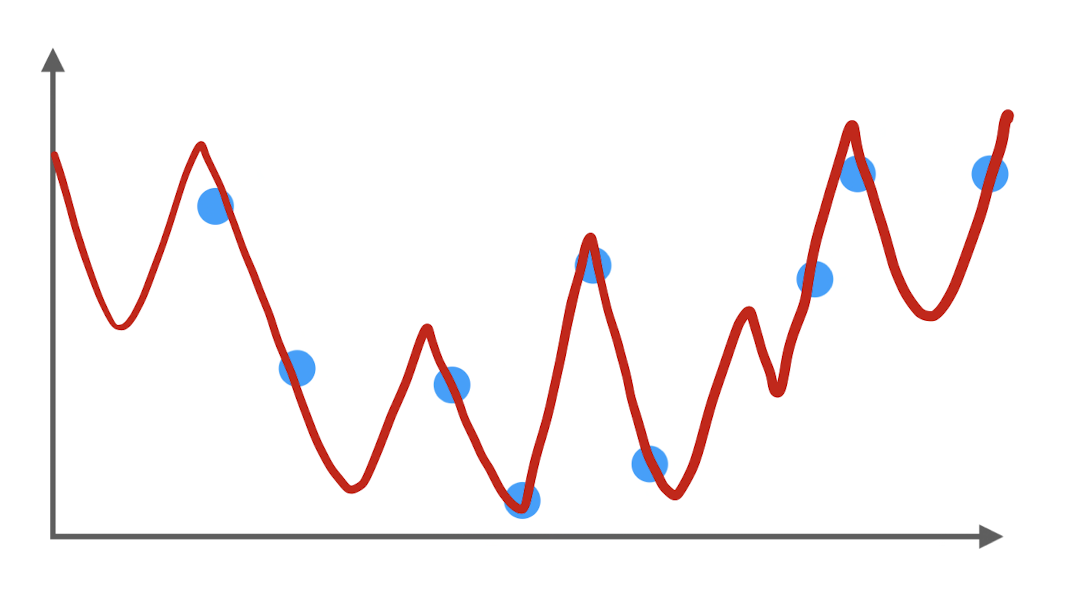
Overfitting
Wenn wir sehr viele Parameter verwenden, können wir komplexe Kurvenverläufe modellieren. Dazu müssen wir das Modell auch entsprechend lang trainieren. Dies führt aber oft zu einem Overfitting. Das Modell (vielleicht ein Polynom hoher Ordnung) deckt zwar alle Trainingsdaten sehr genau ab, man könnte aber vermuten, dass das Modell bei neuen (ungesehenen) Daten eher schlecht abschneidet, weil es die natürlichen Schwankungen der Trainingsdaten zu genau abbildet. Man spricht auch davon, dass das Modell nicht ausreichend generalisiert.
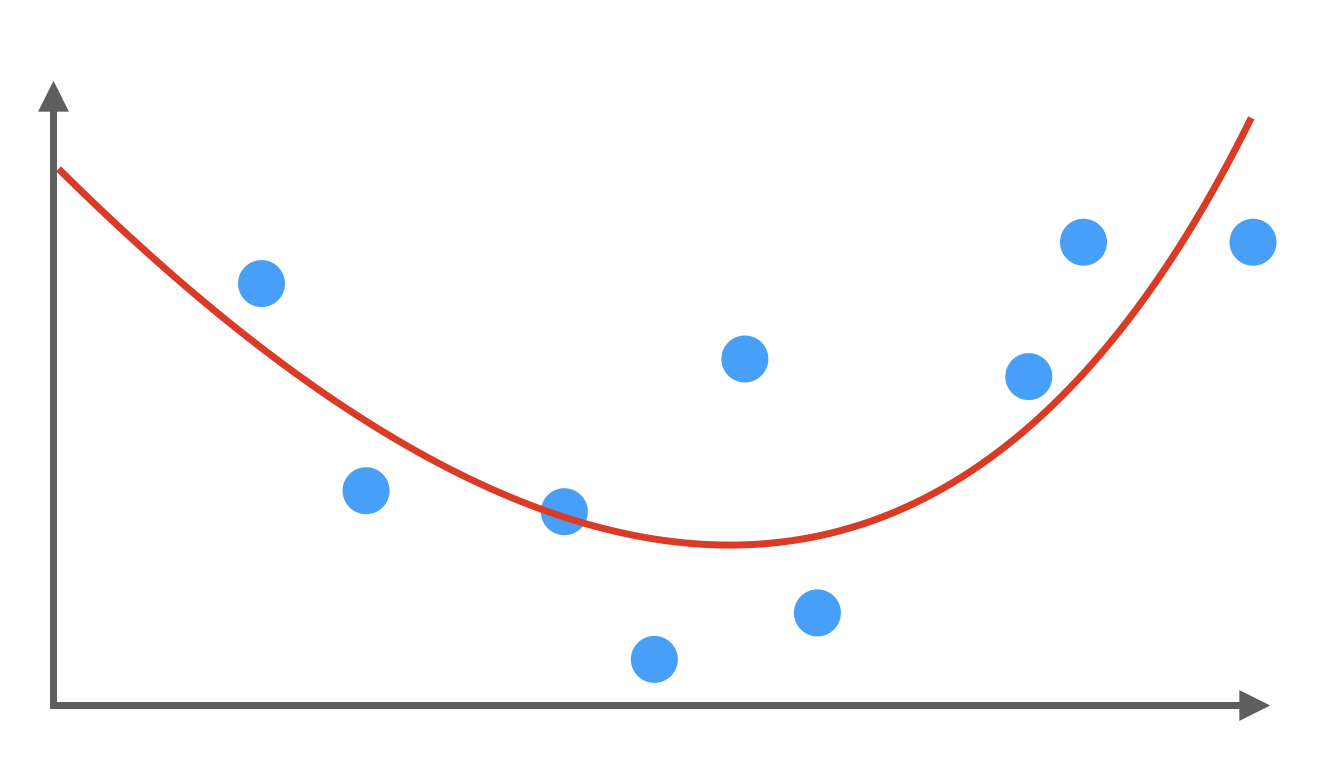
Erwünschtes Modell
Wir wollen eher so etwas wie die folgende Charakteristik. Man kann sich vorstellen, dass neue Datenpunkte in der Nähe der Regressionskurve liegen. Wir haben weder Under- noch Overfitting vorliegen.
In der Praxis ist Overfitting das häufigste Problem (Underfitting weniger). Ganz grob kann man sagen: Overfitting wird oft dadurch verursacht, dass das Modell zu viele Parameter hat, die man zu lange trainiert (also über zu viele Epochen). Ob ein Modell “zu viele” Parameter hat, hängt auch mit der Menge der Trainingsdaten zusammen. Je weniger Daten man hat, umso weniger Parameter sollte auch das Modell haben.
Wie erkennt man Overfitting? Wenn die jeweiligen Fehlerwerte auf Trainings- und Testdaten sehr unterschiedlich sind, dann liegt wahrscheinlich ein Overfitting vor. Man sagt auch, das Modell generalisiere nicht gut. In der Regel wird der Fehler bei Trainingsdaten immer geringer, aber bei Testdaten beginnt er zu steigen. Wenn Sie ein Gütemaß betrachten (Accuracy), ist es umgekehrt: Auf den Trainingsdaten wird die Accuracy stetig höher, aber auf den Testdaten beginnt die Accuracy irgendwann zu sinken.
Wichtige Maßnahmen gegen Overfitting sind
- Parameter reduzieren
- Trainingsdauer (Epochen) reduzieren
- Regularisierung
Regularisierung (und weitere Methoden) werden wir bei den Neuronalen Netzen noch kennenlernen. Es handelt sich dabei um die Einführung eines zusätzlichen Terms in der Fehlerfunktion, um Extremwerte bei den Parametern zu “bestrafen”.
2.4.2 Trainingsdaten vs. Testdaten vs. Validierungsdaten
Wir haben lineare Regression als Beispiel für Maschinelles Lernen kennengelernt. Wie bewerten wir, ob unser Modell “gut” ist? Im Fall der Regression können wir einfach die Zielfunktion \(J\) als Maß für den Fehler unseres Modells verwenden, siehe Formel (ziel) oben. Ein Modell ist also gut, wenn der Fehler möglichst niedrig ist.
Zunächst aber trennen wir unsere Daten sauber – also ohne Überlappung, man nennt das auch disjunkt – in zwei Teile:
- Trainingsdaten (z.B. 80% der Daten)
- Testdaten (z.B. 20% der Daten)
Das Modell darf nur mit Trainingsdaten trainiert werden, so dass das Modell die Testdaten nie “sieht”. Normalerweise durchmischt man die Daten vor der Aufteilung, denn der Testdatensatz soll ja im Idealfall repräsentativ für die Gesamtdaten sein. Die Testdaten nennt man auch Holdout-Daten, da man sie dem Modell im Training vorenthält.
Wir bestimmen dann die Güte des Modells, indem wir den Fehler nur auf den Testdaten berechnen. Das ist unsere Evaluation des Modells. Es soll simulieren, dass das Modell “neue” Daten bekommt.
Die Aufteilung ist z.B. 80:20, wie oben genannt. Natürlich möchte man soviele Trainingsdaten wie möglich für ein möglichst optimales Modell verwenden. Umgekehrt muss man ausreichend Daten für einen aussagekräftigen Test haben. Bei sehr großen Datensätzen mit Millionen von Datenpunkten, kann auch eine Aufteilung 90:10 oder 95:5 sinnvoll sein.
Die Testdaten sind immer die Daten, mit denen man letztendlich die Performanz des Modells misst und publiziert.
In Wettbewerben - wie z.B. auf der Plattform Kaggle - werden oft die Trainingsdaten komplett bereitgestellt. Bei den Testdaten fehlen aber die Zielwerte (also das \(y\)), sind also “geheim”. Die Teilnehmenden eines Wettbewerbs können dann die Vorhersagen des eigenen Modells in Form einer Datei einreichen und die Plattform errechnet die Performance durch den Vergleich mit den geheimen Zielwerten und zeigt das Ergebnis in einer großen Tabelle, dem Leaderboard, an. Beachten Sie, dass Sie beim Erstellen eines solchen Modells natürlich nochmal eigene Testdaten zurückhalten, um ihr Modell zu evaluieren.
Validierungsdaten
In vielen Kontexten wird oft ein dritter Datensatz hinzugenommen, die Validierungsdaten. Diese werden benutzt, wenn man Hyperparameter wie die Lernrate oder die Trainingsdauer optimieren möchte. Warum das sinnvoll ist, wird hoffentlich gleich klar.
Statt die Daten in Trainings- und Testdaten zu teilen, nehmen wir eine Dreiteilung vor:
- Trainingsdaten (70%)
- Validierungsdaten (10%)
- Testdaten (20%)
Die Prozentangaben sind natürlich nur Beispiele bzw. Anhaltspunkte.
Als konkretes Beispiel können Sie sich einen Kaggle-Wettbewerb vorstellen: Hier haben Sie nur die Trainingsdaten gegeben. Die Testdaten sind unbrauchbar, weil die Labels fehlen. Also teilen Sie die Trainingsdaten ist Validierungsdaten und “echte” Trainingsdaten.
Jetzt nehmen wir an, wir möchten die Trainingsdauer festlegen. Wir wissen, dass ein zu langes Trainings (d.h. zu viele Epochen) zu Overfitting führen kann. Wie finden wir also die optimale Trainingsdauer? Beim Training, wo wir nur die Trainingsdaten für die Updates der Parameter (Gewichte) verwenden, messen wir nach jeder Epoche die Accuracy auf den Validierungsdaten (nicht auf den Testdaten). Das könnte wie in Abbildung 2.7 aussehen.
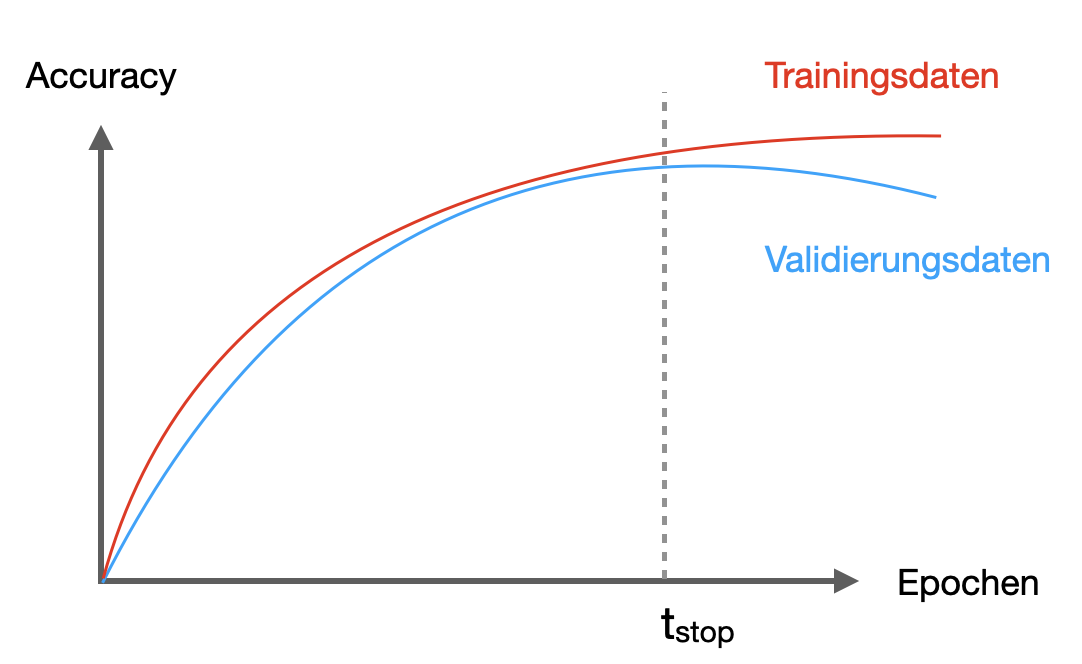
Sobald die Accuracy auf den Validierungsdaten stagniert oder sinkt, stoppen wir das Training, da wir annehmen, dass zu diesem Zeitpunkt die Generalisierungsfähigkeit des Netzes abnimmt. Man nennt diese Technik auch Early Stopping (später in Abschnitt 10.7.4 sehen wir uns an, wie man das in Keras beim Training neuronaler Netze einsetzt).
In Abbildung 2.7 ist es der Zeitpunkt, an dem die Accuracy auf den Validierungsdaten stagniert bzw. sinkt, mit \(t_{stop}\) markiert. Es kann durchaus sein, dass bei anderen Validierungsdaten dieser Zeitpunkt etwas anders ausfallen würde. Und genau das ist der Grund, warum wir \(t_{stop}\) nicht anhand der “echten” Testdaten ermitteln dürfen. Denn letztlich ist auch \(t_{stop}\) ein Parameter - genauer gesagt, ein Hyperparameter - und Daten, die man zum Tunen von Parametern und Hyperparametern verwendet, gelten als vom Modell “gesehen”.
Ist das Modell also derart trainiert mit der vermeindlich optimalen Trainingsdauer \(t_{stop}\), so kann man die Performance auf den tatsächlich “ungesehenen” Testdaten durchführen.
Der Unterschied zwischen Validierungs- und Testdaten ist also, dass die Validierungsdaten bereits während des Trainings (i.d.R. in jeder Epoche) zum Einsatz kommen, um die Performanz des Modell auf “ungesehenen” Daten zu testen, wohingegen die Testdaten erst nach Abschluss des Trainings für einen finalen Test des trainierten und ausgewählten Modells verwendet werden.
2.5 Weiterführende ML-Themen
Im nächsten Kapitel gehen wir direkt zu Neuronalen Netzen über, einem speziellen Bereich des Maschinellen Lernens. Aber natürlich sind Neuronale Netze nur ein kleiner Teil des Gesamtgebiets. Daher gebe ich Ihnen hier ein paar Pointer, wenn Sie sich weiter im Bereich Machine Learning oder Data Analytics umsehen möchten.
Ein paar Methoden, die im Bereich ML heutzutage oft verwendet werden, sind (Links führen zu den entsprechenden Wikipedia-Artikeln, die einen guten ersten Eindruck vermitteln):
Wenn Sie sich im Maschinellen Lernen weiterbilden möchten, kann ich folgende Bücher empfehlen.
Das Hundred-Page Machine Learning Book (Burkov 2019) ist sehr kompakt, aber dennoch ganz gut verstehbar.
Diese zwei Bücher sind Praxis-Bücher mit Python und Jupyter:
Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow (Géron 2022)
Python Machine Learning Cookbook (Gallatin and Albon 2023)
Das akademische Standardwerk zum Thema ist eventuell etwas anstrengend zu lesen:
Pattern Recognition and Machine Learning (Bishop 2007)
Das folgende Buch ist eine persönliche Empfehlung, weil es viel in die Praxis schaut und auch ein Gefühl dafür vermittelt, wo die Grenze zwischen Data Science und Machine Learning verläuft:
The Data Science Design Manual (Skiena 2017)