8 Backpropagation [optional]
In diesem Kapitel leiten wir das Backpropagation-Verfahren für Feedforward-Netze mathematisch her. Genauer gesagt zeigen wir, dass Backpropagation das Konzept des Gradientenabstiegs realisiert. Zunächst entwickeln wir eine Intuition für die Formeln, dann sehen wir uns die mathematische Herleitung der Backpropagation-Formeln an. Dabei wird der Zusammenhang zwischen Zielfunktion, partieller Ableitungen (Gradienten) und Gewichtsanpassung klar. Eine integrale Rolle spielt die Kettenregel und das Konzept der Fehlerwerte \(\delta\).
Nach Abschluss dieses Kapitels können Sie
- den Zusammenhang zwischen Zielfunktion, partieller Ableitung und Gewichtsanpassung erklären
- die Herleitung von Backpropagation mathematisch nachvollziehen und Teilschritte erläutern
- erklären, wie und warum Backpropagation über die Kettenregel von der letzten Schicht rückwärts arbeitet
- erklären, welche Funktion die Fehlerwerte \(\delta\) einnehmen
- den Unterschied zwischen den Bias-Gewichten und den “regulären” Gewichten erklären
Notation
In diesem Kapitel werden wir folgende Notation verwenden.
| Symbol | Bedeutung |
|---|---|
| \(n\) | Anzahl der Eingabeneuronen |
| \(m\) | Anzahl der Ausgabeneuronen |
| \(L\) | Anzahl der Schichten |
| \(n_l\) | Anzahl der Neuronen in Schicht \(l\) |
| \(N\) | Anzahl der Trainingsbeispiele |
| \((x^k, y^k)\) | \(k\)-tes Trainingsbeispiel mit Featurevektor \(x^k\) und korrektem Output \(y^k\) |
| \(W^{(l)}\) | Gewichtsmatrix von Schicht \(l-1\) zu Schicht \(l\) |
| \(b^{(l)}\) | Vektor der Bias-Gewichte von Schicht \(l-1\) zu Schicht \(l\) |
| \(z^{(l)}\) | Rohinput (Vektor) der Neuronen in Schicht \(l\) |
| \(g\) | Aktivierungsfunktion |
| \(a^{(l)}\) | Aktivierung (Vektor) der Neuronen in Schicht \(l\) |
| \(\hat{y}\) | Berechnete Ausgabe (Vorhersage) des Netzwerks bei einer Eingabe \(x\) mit den aktuellen Gewichten |
| \(J\) | Zielfunktion in Form einer Verlustfunktion (loss function), die es zu minimieren gilt |
| \(\lambda\) | Regularisierungsparameter (kommt in \(J\) zum Einsatz) |
| \(\delta^{(l)}\) | Fehlerwerte (Vektor) an den Neuronen in Schicht \(l\) |
In diesem Kapitel versuchen wir, die Formeln für Backpropagation mathematisch herzuleiten. Wir behalten (hoffentlich) dabei stets im Blick, wofür wir diese Formeln eigentlich brauchen.
Es ist tatsächlich nicht leicht, gute Herleitungen zu finden, egal ob in Fachbüchern oder im Internet. Oft werden die Gedankengänge und Herleitungen stark verkürzt dargestellt. Die Darstellung von Michael Nielsen (2015) in seinem Online-Buch Neural Networks and Deep Learning (Chapter 2) ist da eine positive Ausnahme und sei hiermit als Begleitlektüre empfohlen.
Schauen Sie unbedingt auch in Abschnitt ?sec-micrograd, um einen alternativen, allgemeineren Ansatz zu sehen.
8.1 Was haben wir, was müssen wir zeigen?
Bevor wir starten sammeln wir nochmal alle Formeln ein, die relevant sind. Inbesondere listen wir diejenigen Formeln, die wir herleiten möchten.
8.1.1 Verlustfunktion (J)
Wir definieren wir die Verlustfunktion \(J\) für zunächst nur für ein einziges Trainingsbeispiel mit der entsprechend berechnten Ausgabe. Wir summieren über alle \(m\) Ausgabeneuronen:
\[ \tag{J} J_k = - \sum_{i=1}^m y_i^k \; log(\hat{y}_i^k) \]
Diese Funktion heißt Categorical Cross Entropy (siehe Abschnit 4.2.1). Wir werden uns im Folgenden nur mit \(J\) auf diese Funktion beziehen.
Die tatsächliche Kostenfunktion muss alle Trainingsbeispiele \((x^k, y^k)\) mit \(k \in \{1, \ldots, N\}\) berücksichtigen und lautet:
\[ \tag{J2} J = - \frac{1}{N} \sum_{k=1}^N \sum_{i=1}^m y_i^k \; log(\hat{y}_i^k) \]
Das entspricht der Summe der Verluste für die einzelnen Trainingsbeispiele, d.h. der Zusammenhang zwischen (J) und (J2) ist wie folgt:
\[ J = \frac{1}{N} \sum_{k=1}^N J_k \]
Für unsere Herleitung lassen wir den L2-Regularisierungsterm weg bzw. setzen \(\lambda = 0\).
8.1.2 Forward Propagation (Z, A, SM)
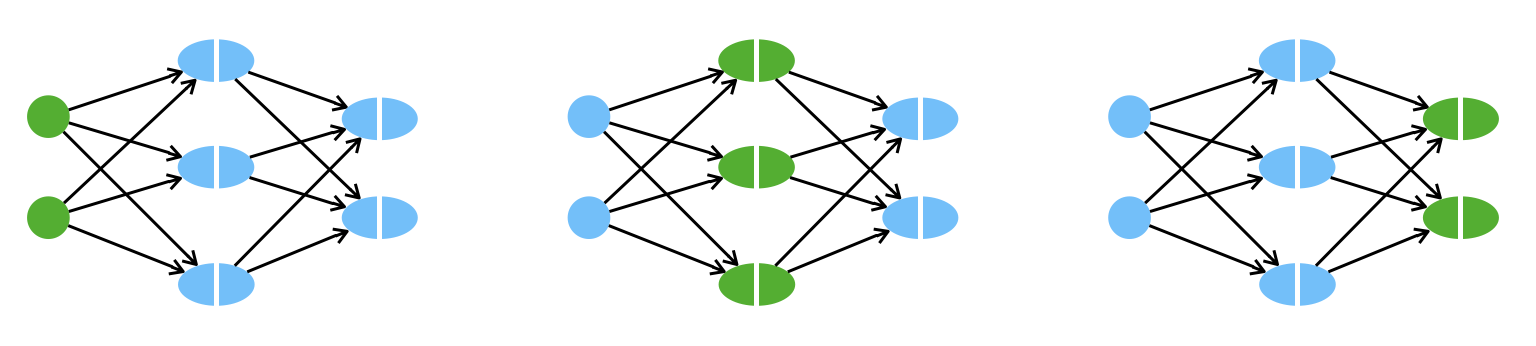
Für die Vorwärtsverarbeitung berechnen wir für jede Schicht \(l\) den Rohinput \(z^{(l)}\) und die Aktivierung \(a^{(l)}\). Diese Formeln müssen wir nicht herleiten, diese haben wir quasi als Funktionsprinzip eines Netzwerks definiert.
Zunächst in der Komponentenschreibweise:
\[ \begin{align*} \tag{Z} z^{(l)}_i &:= \sum_{j=1}^{n_{l-1}}\Big[ w_{i, j}^{(l)} \; a_j^{(l-1)}\Big] + b_i^{(l)} \\[3mm] \tag{A} a_i^{(l)} &= g(z_i^{(l)})\\[3mm] \hat{y}_i &= a^{(L)}_i \end{align*} \]
für alle \(i \in {1, \ldots, n_l}\)
Jetzt in der kompakten Vektorschreibweise:
\[ \begin{align*} z^{(l)} &= W^{(l)} \; a^{(l-1)} + b^{(l)} \\[3mm] a^{(l)} &= g(z^{(l)}) \\[3mm] \hat{y} &= a^{(L)} \end{align*} \]
Für die Ausgabeschicht \(L\) nutzen wir die Softmax-Funktion:
\[ \tag{SM} \hat{y}_i = a^{(L)}_i = g_{sm}(z_i^{(L)}) = \frac{e^{z_i^{(L)}}}{\sum_{j=1}^m e^{z_j^{(L)}}} \]
8.1.3 Backpropagation - herzuleitende Formeln (D1, D2, W, B)

Für die Rückwärtsverarbeitung berechnen wir rückwärts-schichtweise die Fehlerterme \(\delta\) und die Updates für Gewichtsmatrizen \(\Delta W\) und die Updates für die Bias-Vektoren \(\Delta b\). Dies sind die Formeln, die wir herleiten möchten.
\[ \begin{align*} \delta^{(l)} & = \begin{cases} \hat{y} - y & \mbox{wenn}\quad l = L\\[3mm] (W^{(l+1)})^T \; \delta^{l+1} \odot a^{(l)} \odot (1 - a^{(l)})& \mbox{wenn}\quad l \in \{2, \ldots, L-1\} \end{cases}\\[5mm] \tag{DelW} \Delta W^{(l)} & = - \delta^{(l)} \: (a^{(l-1)})^T \\[3mm] \tag{DelB} \Delta b^{(l)} & = - \delta^{(l)} \end{align*} \]
Im Folgenden formulieren wir die Formeln leicht um, damit wir uns in der Herleitung leichter tun.
D1: Fehler an der Ausgabeschicht
Diese Formel berechnet den Fehler (Delta) an der Ausgabeschicht \(L\):
\[ \label{D1}\tag{D1} \delta_j^{(L)} = \hat{y}_j^{(L)} - y_j \]
D2: Fehler an einer Zwischenschicht
Die nächste Formel gibt uns die Möglichkeit, den Fehler an einer Zwischenschicht \(l\) (nicht Ein- oder Ausgabeschicht) zu berechnen:
\[ \delta^{(l)} = \left[ \left( W^{(l+1)} \right)^T \delta^{(l+1)} \right] \odot g'(z^{(l)}) \]
für \(l \in \{1,\ldots, L-1\}\).
Wir leiten die Formel in Komponentenschreibweise her:
\[ \tag{D2}\delta^{(l)}_i = g'(z^{(l)}_i) \sum_{p=1}^{n_{l+1}} w^{(l+1)}_{p,i}\, \delta^{(l+1)}_p \]
W: Gradient der Gewichte
Vielleicht das Wichtigste: Wir wollen anhand der Fehlerterme \(\delta\) die eigentliche Änderungsrate der Gewichte berechnen. Dies ist schließlich der Betrag, den wir für das Update benötigen. Wir betrachten also die Änderung der Gewichte mit Hilfe der Fehlerterme \(\delta\):
\[ \frac{\partial J}{\partial w^{(l)}_{j,k}} = a^{(l-1)}_k \delta^{(l)}_j \label{W}\tag{W} \]
für \(l \in \{1,\ldots, L\}\).
Die Gesamtheit dieser Ableitungen bildet den Gradienten, der in der “Fehlerlandschaft” in Richtung eines hohen Fehlers zeigt. Da wir den Fehler natürlich minimieren wollen, werden bei den eigentlichen Änderungswerten, den \(\Delta w\)’s, die Ableitungen mit einem Minuszeichen versehen (siehe DelW).
B: Gradient der Bias-Gewichte
Ähnlich wie bei (W) betrachten wir die Änderung der Gewichte der Bias-Neuronen:
\[ \frac{\partial J}{\partial b^{(l)}_i} = \delta^{(l)}_i \label{B}\tag{B} \]
für \(l \in \{1,\ldots, L\}\).
Auch hier wird bei den entsprechenden Änderungswerten, den \(\Delta b\)’s (siehe DelB) die Ableitungen negiert.
Jetzt leiten wir die zentralen Backpropagation-Formeln (D1), (D2), (W) und (B) her.
8.2 Intuition und Vorbereitung
8.2.1 Bedeutung des Gradienten
Worum geht es genau? Wir möchten unser Netzwerk so optimieren, dass der Fehler so gering wie möglich wird. Das, was wir verändern, sind die Gewichte des Netzes.
Der Fehler wird mit \(J\) gemessen. Die Frage ist, wie wir die Gewichte \(w\) verändern, damit \(J\) stets etwas kleiner wird. Wir wissen, dass die Ableitung von \(J\) bezüglich eines speziellen \(w\) in die Richtung zeigt, in der \(J\) größer wird. Also nehmen wir den negativen Wert der Ableitung, um \(w\) anzupassen.
Im Kern der Methode steht also, die Ableitung von \(J\) in Bezug auf jedes Gewicht \(w\) zu berechnen.
Genauer gesagt suchen wir alle partiellen Ableitungen
\[ \frac{\partial J}{\partial w^{(l)}_{i,j}} \]
für alle Schichten \(l\in\{1,\ldots,L\}\), wobei \(j \in \{1, \ldots, n_{l-1}\}\) und \(i \in \{1, \ldots, n_{l}\}\). Diese Ableitungen zusammen genommen bilden den Gradienten.
Da wir die Bias-Neuronen gesondert betrachten, wollen wir außerdem die Ableitung der Fehlerfunktion nach den Bias-Gewichten \(b\) herleiten:
\[ \frac{\partial J}{\partial b^{(l)}_{i}} \]
wobei das \(i \in \{1, \ldots, n_l\}\).
Sehen wir uns das in dieser Abbildung an:
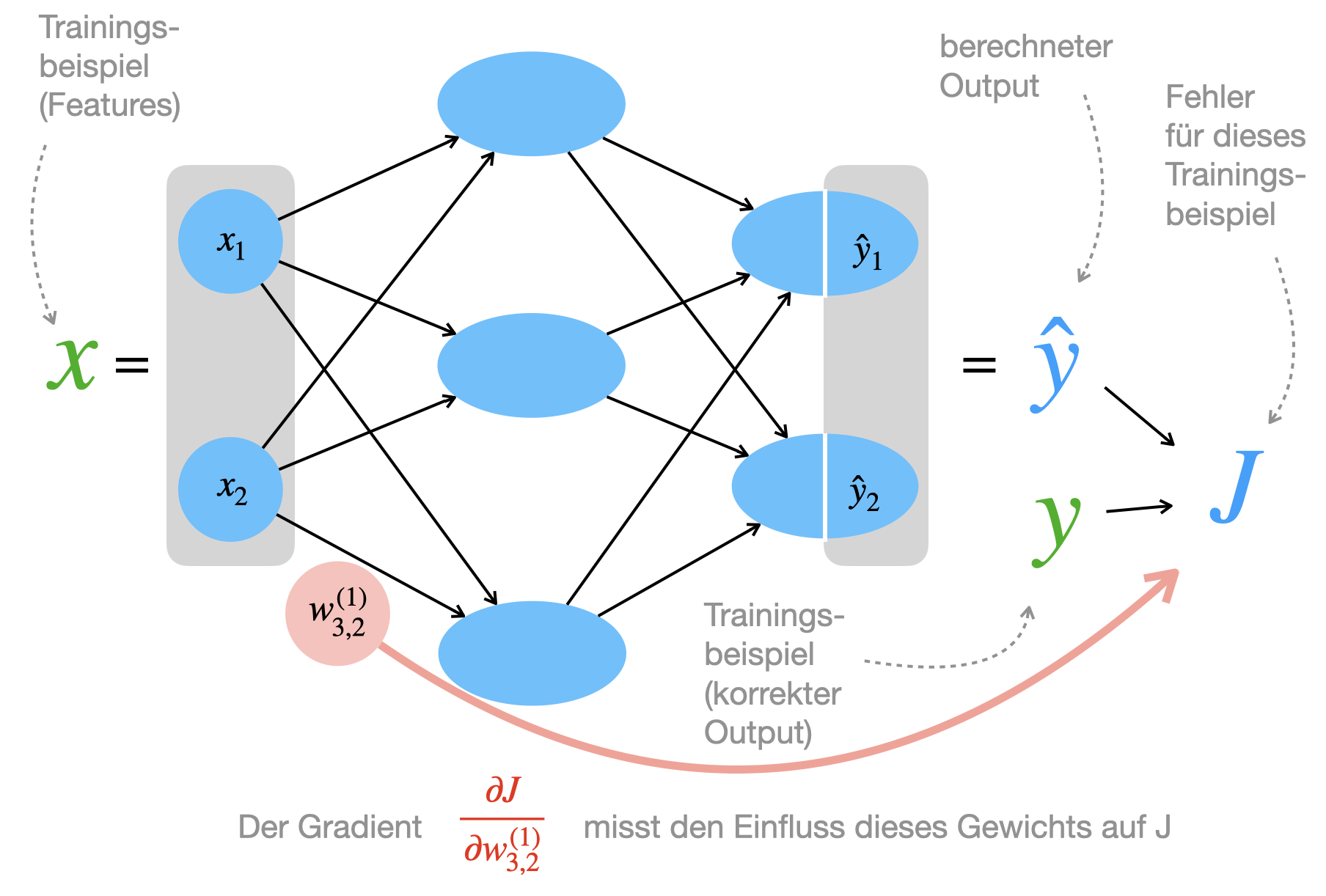
In der Abbildung sehen wir für ein Trainingsbeispiel den Input \(x\) und den berechneten Output \(\hat{y}\). Der Fehler \(J\) arbeitet mit dem korrekten Output \(y\) und dem berechneten Output \(\hat{y}\).
Der Gradient für ein ganz konkretes Gewicht (in diesem Fall \(w_{3,2}^{(1)}\)) ist genau der Zusammenhang zwischen diesem Gewicht und dem Fehler. Ist der Gradient positiv, dann nimmt der Fehler zu, wenn wir das Gewicht erhöhen. Ist der Gradient negativ, dann nimmt der Fehler ab, wenn wir das Gewicht erhöhen. Entsprechend passen wir das Gewicht im Update-Schritt an.
8.2.2 Mehrere Trainingsbeispiele
Nachdem die Bedeutung der Ableitung für ein einziges Gewicht klar geworden ist, machen wir jetzt noch den Schritt zu mehreren Trainingsbeispielen.
Der Fehler \(J\) berechnet sich ja in der Regel aus mehreren Trainingsbeispielen. Wir nehmen mal an, es gäbe nur drei Trainingsbeispiele. Dann ist der Gesamtfehler \(J\) die gemittelte Summe der drei Beispiele:
\[ J = \frac{1}{3} ( J_1 + J_2 + J_3 ) \]
Wenn wir die Ableitung eines Gewichts nehmen, spiegelt diese Ableitung den Einfluss auf diesen Gesamtfehler wieder:
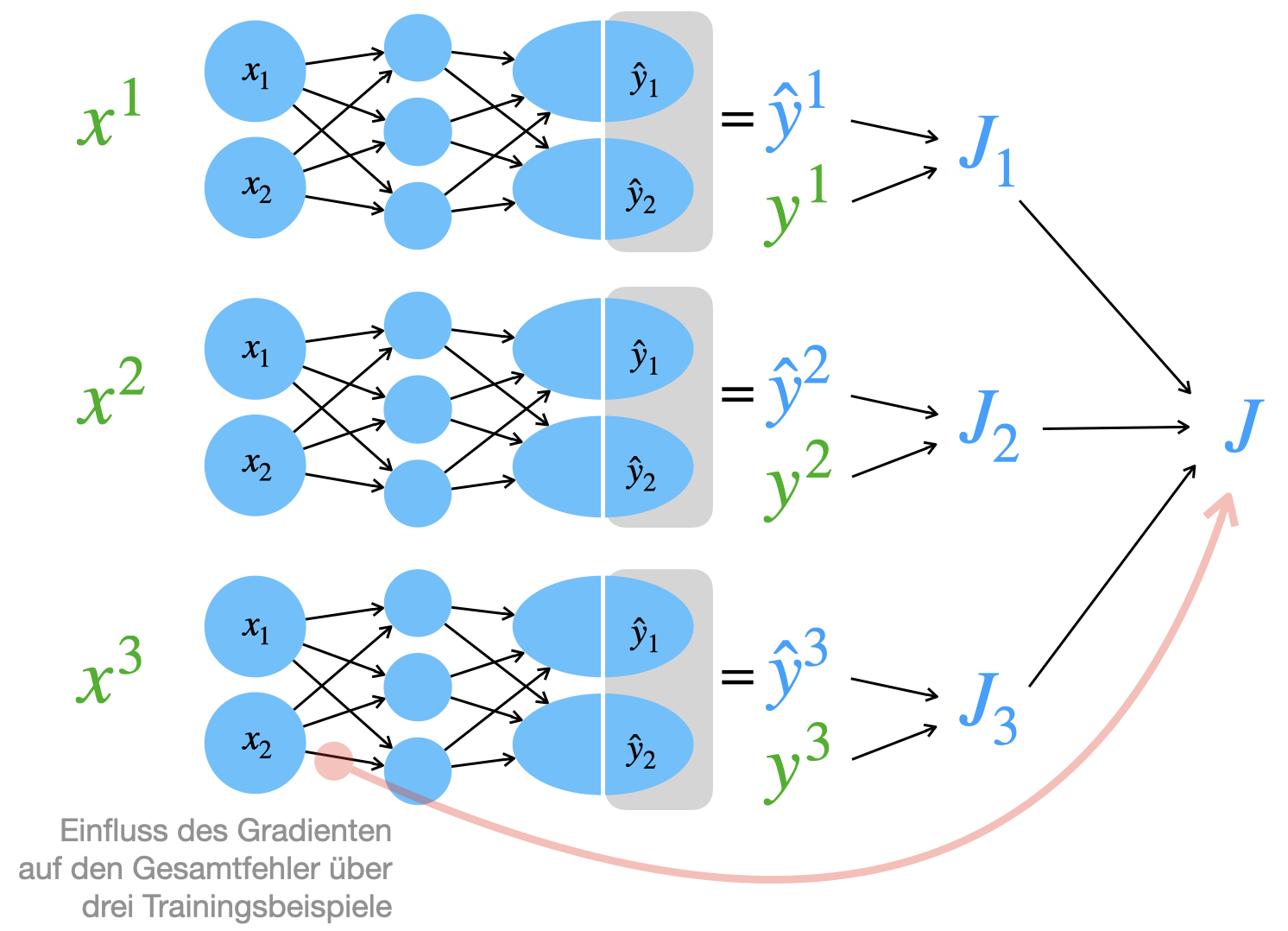
In dem Bild oben sollten Sie beachten, dass für jeden Trainingsbeispiel jeweils eigene Gradienten berechnet werden. Das heißt für das rot markierte Gewicht gibt es den Gradienten für Beispiel 1, 2 und 3.
Im Training werden diese drei Gradienten aufgesammelt und dann gemittelt zum Gewichtsupdate genutzt.
Sehen wir uns das konkreter an (wir lassen den Faktor \(\frac{1}{3}\) weg):
\[ \begin{align*} J &= J_1 + J_2 + J_3\\ &= - \sum_{i=1}^m y_i^1 \; log(\hat{y}_i^1) - \sum_{i=1}^m y_i^2 \; log(\hat{y}_i^2) - \sum_{i=1}^m y_i^3 \; log(\hat{y}_i^3) \end{align*} \]
Jetzt nehmen wir an, dass die beiden korrekten Kategorien \(i_1, i_2\) und \(i_3\) sind (da sind die entsprechenden \(y\)’s gleich 1):
\[ J = - log(\hat{y}_{i_1}^1) -log(\hat{y}_{i_2}^2) -log(\hat{y}_{i_3}^2) \]
Jetzt überlegen Sie, wie Sie hier sukzessive die Formeln einsetzen, um diese drei Summanden für drei Trainingsbeispiele aufzulösen:
\[ \begin{align*} \hat{y} &= a^{(L)} \\[1mm] a^{(L)} &= g(z^{(L)}) \\[1mm] z^{(L)} &= W^{(L)} \; a^{(L-1)} + b^{(L)} \\[1mm] a^{(L-1)} &= g(z^{(L-1)}) \\[1mm] z^{(L-1)} &= W^{(L-1)} \; a^{(L-2)} + b^{(L-1)} \\[1mm] &\dots \end{align*} \]
Und bedenken Sie, dass bei den Matrizenmultiplikationen mit den \(W\)’s und den \(a\)’s ganz normale Summen entstehen:
\[ z^{(l)}_i = \sum_{j=1}^{n_{l-1}}\Big[ w_{i, j}^{(l)} \; a_j^{(l-1)}\Big] b_i^{(l)} \]
Dann haben Sie, wenn alle Gleichungen eingesetzt sind und alle Summen aufgelöst sind, tatsächlich eine lange Summe da stehen, vielleicht durchsetzt von Exponentialfunktionen (wegen der Aktivierungsfunktion). Aber Sie können sich vorstellen, dass man diesen langen Term relativ leicht bezüglich eines ganz bestimmten Gewichts ableiten kann. Und darauf basiert Gradientenabstieg und Backpropagation.
8.2.3 Bedeutung des \(\delta\)
Da wir bereits den Backpropagation-Algorithmus gesehen haben, dürften Sie sich zu recht fragen, was das \(\delta\) eigentlich bedeutet, das bislang als “Fehler” bezeichnet wurde. Tatsächlich handelt es sich um die Ableitung von \(J\) nach den Rohinputs der einzelnen Neuronen.
Formal:
\[\delta^{(l)}_i := \frac{\partial J}{\partial z_i^{(l)}} \]
Man kann auch sagen, die Deltawert-Vektoren sind die Gradienten der Rohinput-Vektoren.
Was wir ja eigentlich suchen, ist die Ableitung von \(J\) nach den jeweiligen Gewichten, aber die Deltawerte sind ein nützliches Zwischenergebnis bei der schrittweisen Berechnung der Gewichtsgradienten. Das hängt wiederum mit der Kettenregel zusammen. Wir sehen hoffentlich im Verlauf des Kapitels, warum diese Definition der Deltawerte sinnvoll ist.
8.2.4 Netz mit zwei Schichten
Wir betrachten zunächst ein Netz mit nur zwei Schichten und verallgemeinern im Anschluss auf ein Netz mit beliebig vielen Schichten. Sie werden sehen, dass man mit drei Schichten alle Fälle abdeckt.
Die folgende Abbildung ist eine reduzierte Darstellung des Beispielnetzes. Die Anzahl der Neuronen pro Schicht ist aber allgemein gehalten über die Bezeichnung \(n_l\), wobei \(l\in\{1,2\}\) die Schicht angibt.
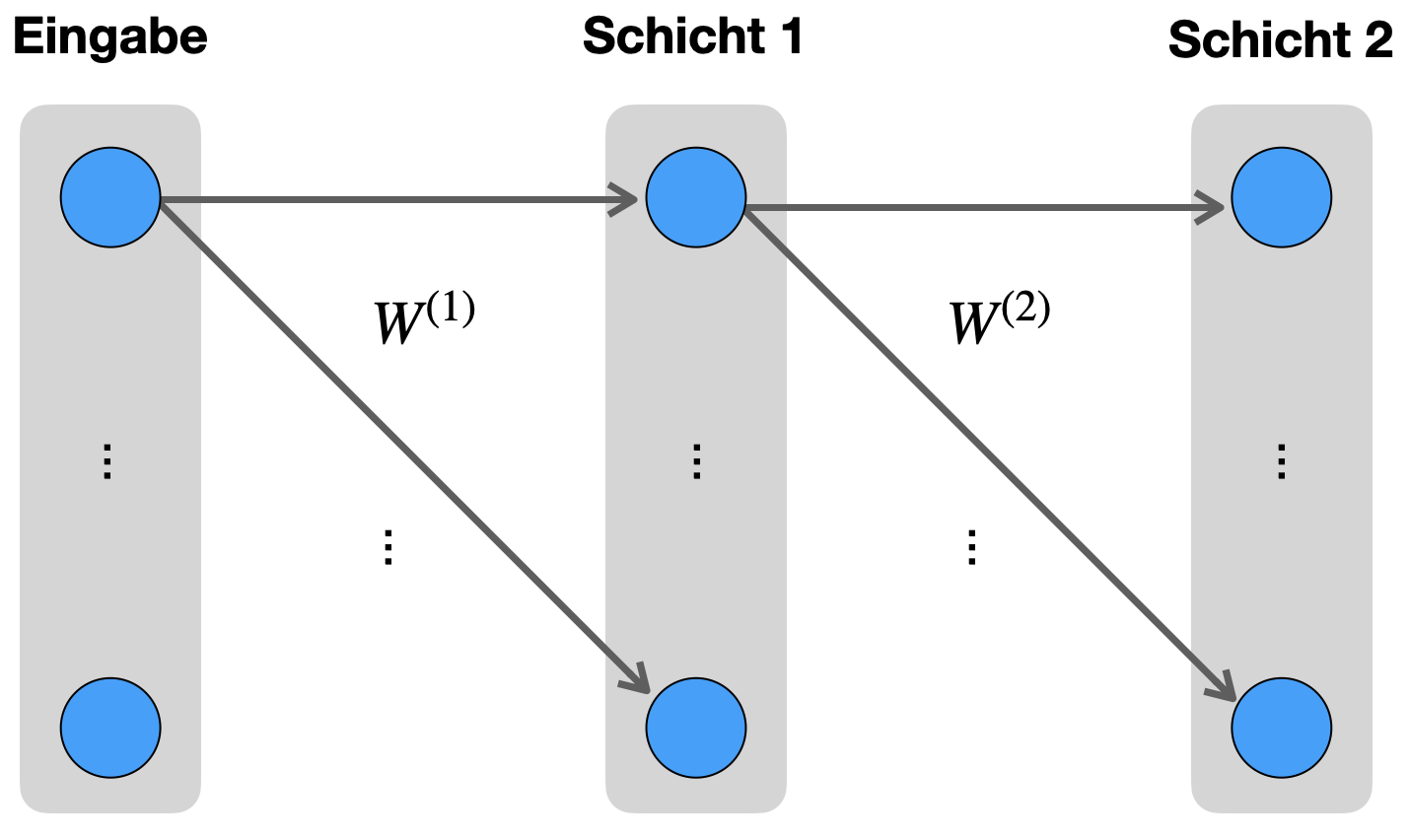
Warum betrachten wir ein 2-Schichten-Netz? In der Herleitung von Backpropagation unterscheidet man auch im allgemeinen Fall (mit beliebig vielen Schichten) nur zwischen den Gewichten zur Ausgabeschicht und allen anderen Gewichten. Dies kann man auch bei einem 2-Schichten-Netzwerk tun.
Wir gehen in zwei Schritten vor. Zunächst betrachten wir ein Gewicht zur letzten Schicht.
8.3 Schritt 1: Gewicht zur Ausgabeschicht
Da Backpropagation von Schicht 2 zu Schicht 1 arbeitet, wählen wir zunächst eines der “hinteren” Gewichte, also ein Gewicht aus \(W^{(2)}\). Wir nennen dieses einzelne Gewicht \(w^{(2)}_{i,j}\), es befindet sich irgendwo zwischen der ersten und zweiten Schicht.
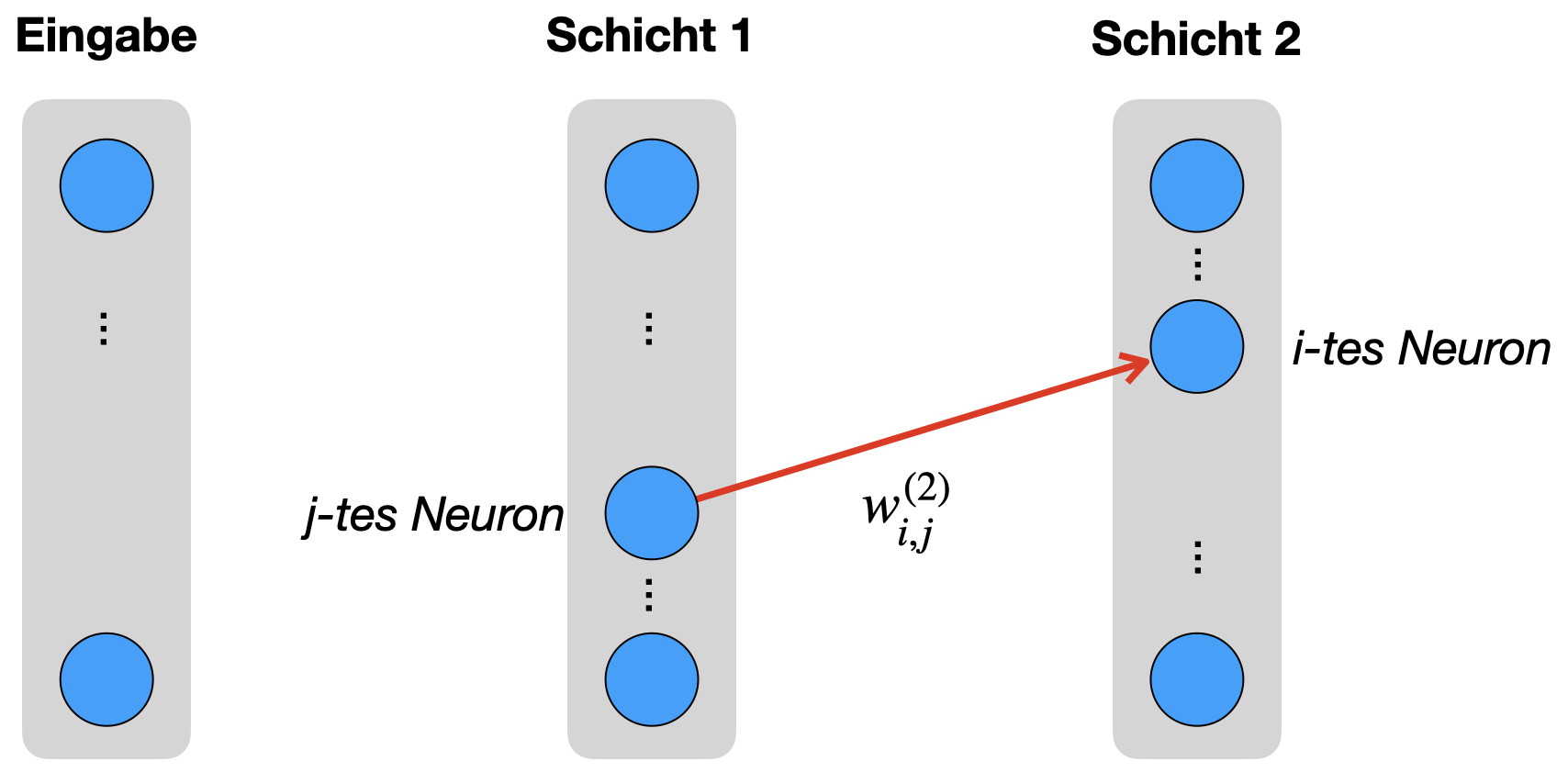
Um \(w^{(2)}_{i,j}\) zu verändern, wollen wir wissen, wie sich die Fehlerfunktion \(J\) verhält, wenn wir \(w^{(2)}_{i,j}\) ein bisschen kleiner oder größer machen. Genau das sagt uns die Ableitung von \(J\) nach \(w^{(2)}_{i,j}\), also
\[ \tag{a} \frac{\partial J}{\partial w^{(2)}_{i,j}} \]
Wir schauen uns die Fehlerfunktion \(J\) an (wir haben den Index für die Summe hier \(p\) genannt, damit es keine Verwechslungen mit dem \(i\) in \(w^{(2)}_{i,j}\) gibt; außerdem lassen wir die Summe über alle Trainingsbeispiele weg):
\[ J = - \sum_{p=1}^m y_p \; log(\hat{y}_p) \]
Wir sehen, dass \(w^{(2)}_{i,j}\) nicht direkt in \(J\) enthalten ist. Wie können wir also Ableitung (a) finden? Dazu benötigen wir die Kettenregel. Hier wiederum müssen wir zunächst klären, welche Parameter sich in welchen anderen Parametern “verstecken”. Ausgangspunkt ist die berechnete Ausgabe \(\hat{y}\). Zur Erinnerung: \(y\) ist der vom Trainingsbeispiel vorgegebene Zielwert, ist also eine Konstante.
Wenn man - wie in Abbildung 8.3 - vom Gewicht \(w^{(2)}_{i,j}\) ausgeht, dann steckt das Gewicht in der Berechnung eines Rohinputs \(z_i^{(2)}\), der wiederum zu \(\hat{y}_i\) führt. Genauer gesagt zeigt unser Gewicht auf Neuron \(i\) in Schicht 2 und geht also dort in die Berechnung des Rohinputs des i-ten Neurons ein, also in \(z^{(2)}_i\). Wir sehen das an der Berechnungsformel (Z):
\[ z_i^{(2)} = \sum_{p=1}^{n_{1}} w^{(2)}_{i,p} \; a_p^{(1)} \]
Daher können wir die Ableitung (a) mit Hilfe der Kettenregel umformulieren:
\[ \tag{b} \frac{\partial J}{\partial w^{(2)}_{i,j}} = \underbrace{ \frac{\partial J}{\partial z^{(2)}_i}}_{(**)} \, \underbrace{\frac{\partial z^{(2)}_i} {\partial w^{(2)}_{i,j}}}_{(*)}\]
Wir sehen uns zunächst mal den Faktor \((*)\) an: Hier setzen wir die Formel (Z) für \(z^{(2)}_i\) ein und lösen auf.
\[ \frac{\partial z^{(2)}_i}{\partial w^{(2)}_{i,j}} = \frac{\partial }{\partial w^{(2)}_{i,j}} \left( \sum_{p=1}^{n_1} w^{(2)}_{i,p} \; a_p^{(1)} + b_i^{(2)} \right) = a_j^{(1)} \]
Ihnen ist der Schritt zu \(a_j^{(1)}\) nicht klar? Vielleicht hilft Ihnen diese Darstellung der Summe:
\[ \sum_{p=1}^{n_1} w^{(2)}_{i,p} \; a_p^{(1)} + b_i^{(2)} = w^{(2)}_{i,1} \; a_1^{(1)} + w^{(2)}_{i,2} \; a_2^{(1)} + \ldots + w^{(2)}_{i,n_l} \; a_{n_l}^{(1)} + b_i^{(2)} \]
Bei der Ableitung “nach \(w^{(2)}_{i,j}\)” fällt das \(b_i^{(2)}\) weg (Konstante) und von den anderen Summanden bleibt nur der Faktor vor \(w^{(2)}_{i,j}\) übrig:
\[ \frac{\partial }{\partial w^{(2)}_{i,j}} \left( w^{(2)}_{i,1} \; a_1^{(1)} + w^{(2)}_{i,2} \; a_2^{(1)} + \ldots + w^{(2)}_{i,n_l} \; a_{n_l}^{(1)} + b_i^{(2)} \right) = a_j^{(1)} \]
Formel (b) wird durch die obige Formel zu:
\[ \tag{c} \frac{\partial J}{\partial w^{(2)}_{i,j}} = \underbrace{\frac{\partial J}{\partial z^{(2)}_i}}_{(**)} \, a_j^{(1)}\]
Wir lösen jetzt den Faktor \((**)\) auf: Dazu setzen wir die Formel (J) für die Verlustfunktion \(J\) ein. Wir lassen die Summe über die Trainingsbeispiele erst einmal weg.
\[ \begin{align*} \frac{\partial J}{\partial z^{(2)}_i} &= \frac{\partial }{\partial z^{(2)}_i}\Big( - \sum_{p=1}^m y_p \; log(\hat{y}_p) \Big)\\[4mm] &= - \sum_{p=1}^m y_p \; \frac{\partial }{\partial z^{(2)}_i} log(\hat{y}_p)\\[4mm] &= - \sum_{p=1}^m \frac{y_p}{\hat{y}_p} \frac{\partial \hat{y}_p}{\partial z^{(2)}_i} \end{align*} \]
An dieser Stelle verwenden wir bei \(\hat{y}_p\) die Ableitung der Softmax-Funktion (SM-Ab), die wir unten herleiten:
\[ \begin{align*} \frac{\partial J}{\partial z^{(2)}_i} &= - \sum_{p=1}^m \frac{y_p}{\hat{y}_p} \frac{\partial \hat{y}_p}{\partial z^{(2)}_i} \\[4mm] &= - \sum_{p=1}^m \frac{y_p}{\hat{y}_p} \, \hat{y}_p (1_{i=p} - \hat{y}_i) \tag{SM-Ab} \\[4mm] &= - \sum_{p=1}^m y_p \, (1_{i=p} - \hat{y}_i)\\[4mm] &= - \sum_{p=1}^m y_p \, 1_{i=p} + \sum_{p=1}^m y_p \hat{y}_i \\[4mm] &= - y_i + \hat{y}_i \tag{*} \\[4mm] &= \hat{y}_i - y_i \end{align*} \]
Ihnen ist der Übergang auf Zeile \((*)\) nicht klar?
Erste mögliche Problemstelle:
\[ \sum_{p=1}^m y_p \, 1_{i=p} = y_i \]
Der Ausdruck \(1_{i=p}\) bedeutet, dass er dann \(1\) ist, wenn der Laufindex \(p\) der Summe das \(i\) erreicht und sonst einfach \(0\) wird (das wird unten bei der Ableitung von Softmax erklärt). Sehen wir uns die Summe ausgeschrieben an:
\[ \sum_{p=1}^m y_p \, 1_{i=p} = y_1 \, 1_{i=1} + y_2 \, 1_{i=2} + \ldots + y_m \, 1_{i=m} \]
Das \(1_{i=p}\) wird fast immer Null, nur nicht an der Stelle \(i\). Also bleibt nur das \(y_i\) übrig.
Zweite mögliche Problemstelle:
\[ \sum_{p=1}^m y_p \hat{y}_i = \hat{y}_i \]
Hier müssen Sie daran denken, dass \(y\) ein One-Hot-Vektor ist, d.h. genau eine Komponente ist \(1\), alle anderen sind \(0\). Beachten Sie außerdem, dass der Index \(i\) nichts mit der Summe zu tun hat (dort ist der Laufparameter ja \(p\)). Dann können Sie das so hinschreiben:
\[ \begin{align*} \sum_{p=1}^m y_p \hat{y}_i &= \hat{y}_i \sum_{p=1}^m y_p \\ &= \hat{y}_i \end{align*} \]
Wenn wir das von oben in (c) einsetzen, bekommen wir:
\[ \tag{d}\frac{\partial J}{\partial w^{(2)}_{i,j}} = \big( \hat{y}_i - y_i \big) \, a_j^{(1)}\]
8.3.1 Ableitung der Softmax-Funktion
In der Ausgabeschicht \(L\) verwenden wir die Softmax-Funktion (SM), um den Output \(\hat{y}\) zu definieren. Die Rohinputs sind \(z_1^{(L)}, \ldots, z_m^{(L)}\), wir schreiben aber der Einfachheit halber nur \(z_1, \ldots, z_m\). Dann gilt:
\[ \hat{y}_p = \frac{e^{z_p}}{\sum_{j=1}^m e^{z_j}} \]
Wir benötigen die folgende partielle Ableitung (für alle \(i \in {1, \ldots, m}\)):
\[ \frac{\partial \hat{y}_p}{\partial z_i} \]
Wir unterscheiden zwei Fälle:
Fall \(i = p\):
Wir wenden hier hauptsächlich die Quotientenregel beim Ableiten an.
\[ \begin{align*} \frac{\partial \hat{y}_i}{\partial z_i} &= \frac{\partial }{\partial z_i} \frac{e^{z_i}}{\sum_{j=1}^m e^{z_j}}\\[4mm] &= \frac{e^{z_i} \sum_{j=1}^m e^{z_j} - e^{z_i} e^{z_i}}{(\sum_{j=1}^m e^{z_j})^2}\\[4mm] &= \frac{e^{z_i} }{\sum_{j=1}^m e^{z_j}} \Big( 1 - \frac{e^{z_i} }{\sum_{j=1}^m e^{z_j}} \Big)\\[4mm] &= \hat{y}_i ( 1- \hat{y}_i) \end{align*} \]
Fall \(i \neq p\):
\[ \begin{align*} \frac{\partial \hat{y}_p}{\partial z_i} &= \frac{\partial }{\partial z_i} \frac{e^{z_p}}{\sum_{j=1}^m e^{z_j}}\\[4mm] &= \frac{- e^{z_p} e^{z_i}}{(\sum_{j=1}^m e^{z_j})^2}\\[4mm] &= - \frac{e^{z_p}}{\sum_{j=1}^m e^{z_j}} \frac{e^{z_i}}{\sum_{j=1}^m e^{z_j}}\\[4mm] &= - \hat{y}_p \hat{y}_i \end{align*} \]
Ist dieser Übergang nicht klar?
\[ \frac{\partial }{\partial z_i} \frac{e^{z_p}}{\sum_{j=1}^m e^{z_j}} = \frac{- e^{z_p} e^{z_i}}{(\sum_{j=1}^m e^{z_j})^2} \]
Sie müssen hier ebenfalls die Quotientenregel anwenden. Ansonsten machen Sie sich folgende Identitäten klar, dann müssten Sie es verstehen.
Da \(z_p\) für diese Ableitung eine Konstante ist, gilt:
\[ \frac{\partial }{\partial z_i} e^{z_p} = 0 \]
Und bei der folgenden Summe bleibt nur der Summand an der Stelle \(i\) übrig, die anderen werden Null. Man sollte natürlich auch wissen, dass die Ableitung von \(e^x\) wieder \(e^x\) ist:
\[ \frac{\partial }{\partial z_i} {\sum_{j=1}^m e^{z_j}} = e^{z_i} \]
Um das Ergebnis kompakt zu halten, verwenden wir folgende Schreibweise:
\[ 1_{i=p} := \begin{cases} 1 &\mbox{wenn}\quad i = p\\ 0 &\mbox{wenn}\quad i \neq p \end{cases} \]
Dann können wir schreiben:
\[ \tag{SM-Ab} \frac{\partial \hat{y}_p}{\partial z_i} = \hat{y}_p (1_{i=p} - \hat{y}_i) \]
8.3.2 Fehlerterm \(\delta\)
Betrachten wir noch einmal das obige Ergebnis (c) und definieren den ersten Faktor als Fehlerterm \(\delta^{(2)}_i\).
\[ \frac{\partial J}{\partial w^{(2)}_{i,j}} = \underbrace{\frac{\partial J}{\partial z^{(2)}_i}}_{\delta_i^{(2)}} \, a_j^{(1)}\]
Das heißt wir definieren
\[\tag{D1} \delta^{(2)}_i := \frac{\partial J}{\partial z_i^{(2)}} \]
Für unsere konkrete Situation bedeutet das (siehe d):
\[ \delta^{(2)}_i = \hat{y}_i - y_i \]
Jetzt können wir die Ableitung von \(J\) so darstellen:
\[\frac{\partial J}{\partial w^{(2)}_{i,j}} = a_j^{(1)} \, \delta^{(2)}_i \]
Im nächsten Schritt wird klar, warum diese Definition eines Fehlerterms sinnvoll ist.
8.3.3 Verallgemeinerung (D1, W’)
Da wir in unserer Herleitung immer von der “letzten Schicht” gesprochen haben, können die obige Herleitung auf ein Netz mit \(L\) Schichten verallgemeinern.
Wir halten fest:
\[ \begin{align} \tag{D1}\delta^{(L)}_i &= \hat{y}_i - y_i \\[3mm] \tag{W'}\frac{\partial J}{\partial w^{(L)}_{i,j}} &= a_j^{(L-1)}\, \delta^{(L)}_i \end{align} \]
Wir haben somit (D1) hergeleitet und (W) für den Fall, dass \(l = L\) ist, hergeleitet.
8.4 Schritt 2: Gewicht zu einer Zwischenschicht
Jetzt betrachten wir in unserem Netz ein beliebiges Gewicht zwischen Eingabeschicht und Schicht 1. Wie wir später sehen, ist dieses Gewicht repräsentativ für das Gewicht einer Verbindung, die nicht in die Ausgabeschicht zeigt. Das heißt, wie benötigen nur diese zwei Schritte für die komplette Herleitung.
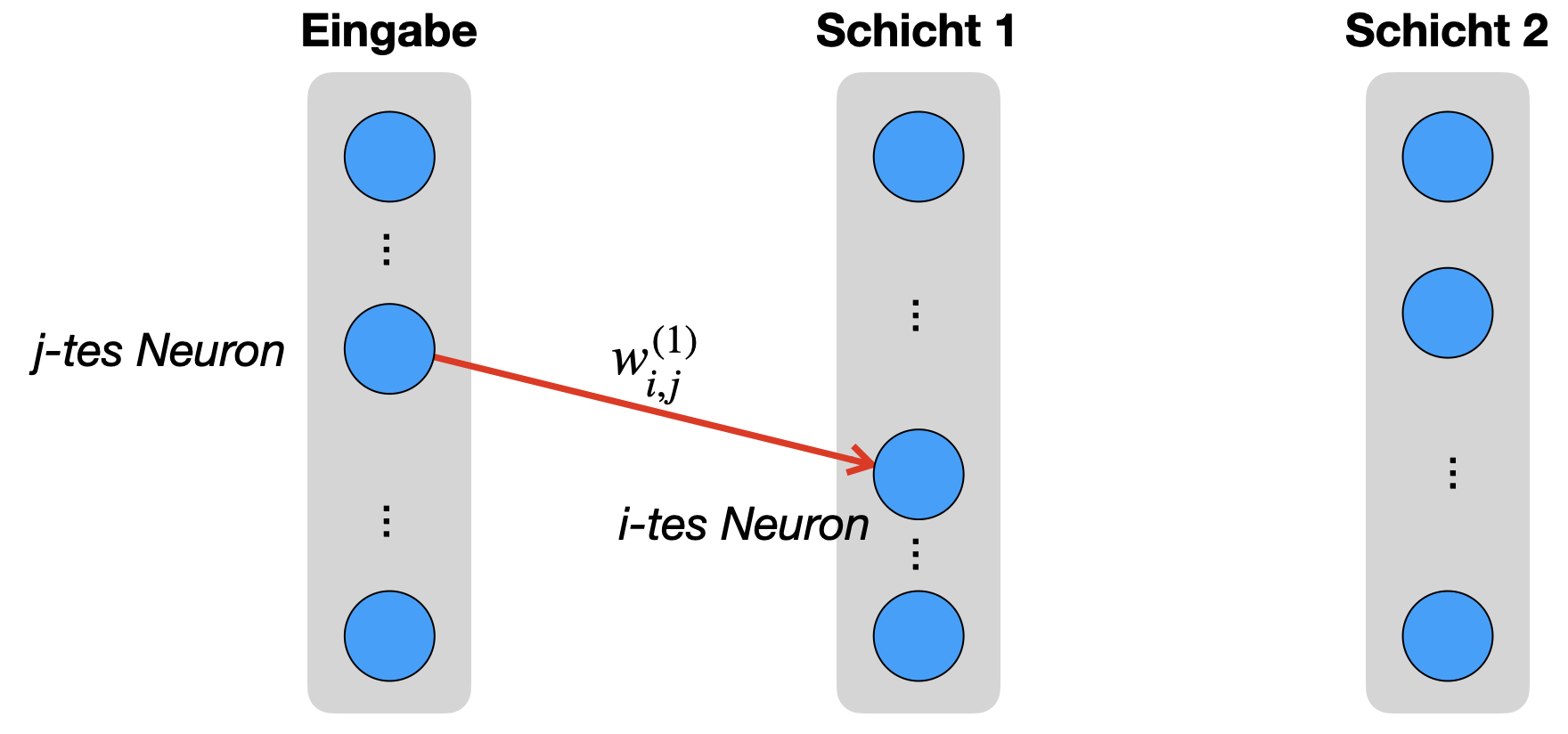
Man beachte, dass die Indizes \(i\) und \(j\) jetzt möglicherweise andere Indizes sind als beim Gewicht in Schritt 1.
8.4.1 Ziel
Wir erinnern uns wieder an unser Ziel: Die Ableitung der Fehlerfunktion \(J\) nach einem Gewicht \(w^{(1)}_{i,j}\):
\[ \tag{a} \frac{\partial J}{\partial w^{(1)}_{i,j}} \]
Auch hier fragen wir uns wieder: Welche Abhängigkeiten gibt es auf dem “Weg” von Gewicht \(w^{(1)}_{i,j}\) in Richtung Ausgabeschicht bis zu \(J\)? Anders gesagt: In welche Berechnungen (bei Forward Propagation) fließt unser \(w^{(1)}_{i,j}\) ein?
8.4.2 Abhängigkeiten
In der folgenden Abbildung sehen wir, dass der Weg von \(w^{(1)}_{i,j}\) in Richtung Ausgabe zunächst zum Rohinput \(z^{(1)}_i\) führt. Von Schicht 1 zu Schicht 2 sieht man aber, dass der Wert in alle Neuronen der nächsten Schicht eingeht (graue Pfeile). Das muss sich später in den Formeln natürlich widerspiegeln.
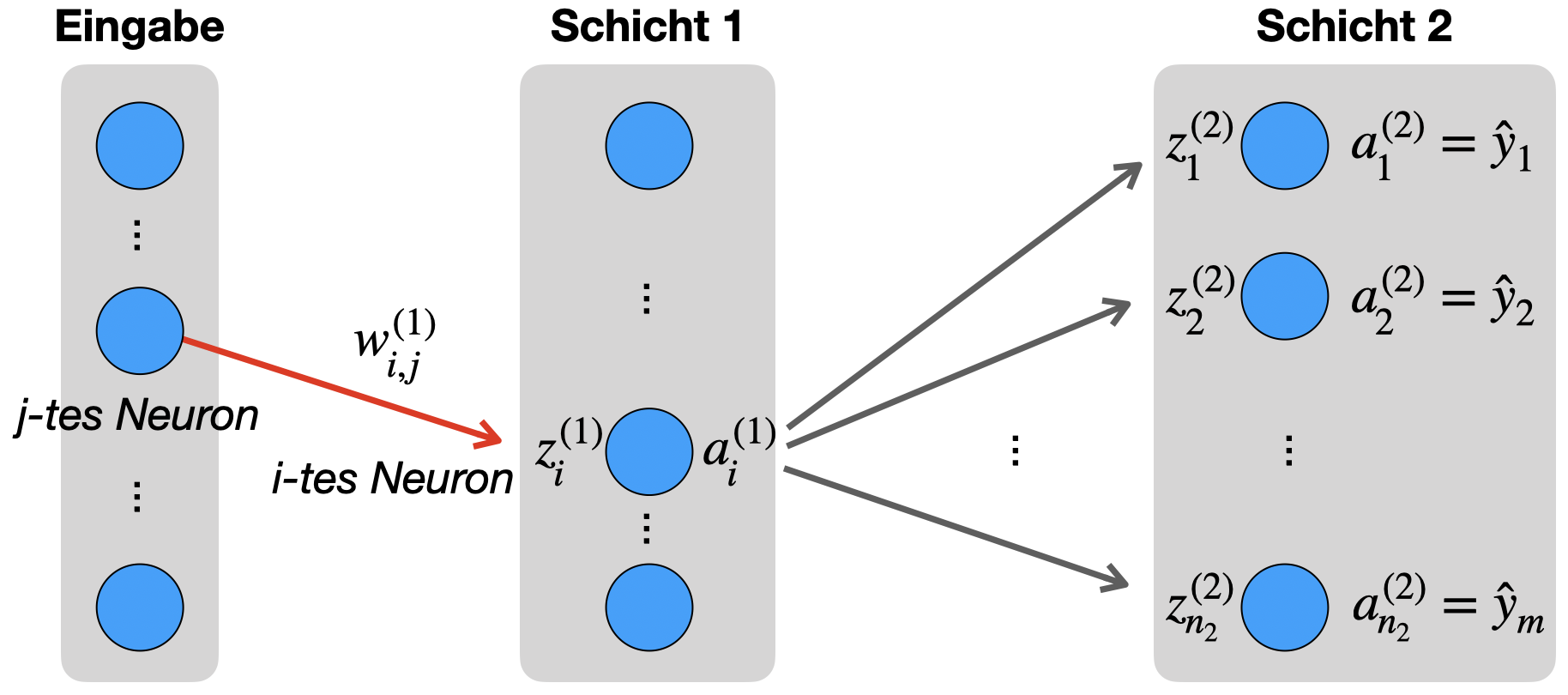
8.4.3 Kettenregel: Zwischen Eingabe und Schicht 1
Wir wenden auch hier wieder die Kettenregel schrittweise an. Wir betrachten jetzt den roten Pfeil und pflegen in Formel (a) den Einfluss auf \(z^{(1)}_i\) ein (in anderen Worten: \(w^{(1)}_{i,j}\) ist in der Formel \(z^{(1)}_i\) enthalten):
\[ \tag{b} \frac{\partial J}{\partial w^{(1)}_{i,j}} = \frac{\partial J}{\partial z^{(1)}_i} \frac{\partial z^{(1)}_i}{\partial w^{(1)}_{i,j}}\]
Wir bleiben beim roten Pfeil und bilden den Einfluss auf \(a^{(1)}_i\) ab:
\[ \tag{c} \frac{\partial J}{\partial w^{(1)}_{i,j}} = \frac{\partial J}{\partial a^{(1)}_i} \frac{\partial a^{(1)}_i}{\partial z^{(1)}_i}\frac{\partial z^{(1)}_i}{\partial w^{(1)}_{i,j}}\]
8.4.4 Kettenregel: Zwischen Schicht 1 und 2
Der nächste Schritt sind die grauen Pfeile rechts. Das ist schwieriger, denn - wie man sieht - hat das \(a^{(1)}_i\) Einfluss auf alle Rohinputs \(z^{(2)}_p\) der Schicht 2. Wir können das durch den Vektor \(z^{(2)}\) ausdrücken:
\[ \frac{\partial J}{\partial w^{(1)}_{i,j}} = \underbrace{\frac{\partial J}{\partial z^{(2)}} \frac{\partial z^{(2)}}{\partial a^{(1)}_i}}_{\text{Einfluss auf Schicht 2}} \quad \frac{\partial a^{(1)}_i}{\partial z^{(1)}_i} \quad \frac{\partial z^{(1)}_i}{\partial w^{(1)}_{i,j}} \]
Das kann man erstmal so hinschreiben, sollte aber beachten, dass die ersten zwei Faktoren Vektoren sind, d.h. es handelt sich um ein Skalarprodukt.
Wir gehen wie schon beim ersten Schritt die drei Faktoren durch:
\[ \tag{d} \frac{\partial J}{\partial w^{(1)}_{i,j}} = \underbrace{\frac{\partial J}{\partial z^{(2)}} \frac{\partial z^{(2)}}{\partial a^{(1)}_i}}_{(1)} \quad \underbrace{\frac{\partial a^{(1)}_i}{\partial z^{(1)}_i}}_{(2)} \quad \underbrace{\frac{\partial z^{(1)}_i}{\partial w^{(1)}_{i,j}}}_{(3)} \]
Zu (1):
Jetzt muss man sich erstmal vor Augen führe, wie diese zwei Vektoren aussehen. Beide haben die Länge \(n_2\) = Anzahl der Neuronen in der zweiten Schicht:
\[ \frac{\partial J}{\partial z^{(2)}} = \begin{pmatrix} \frac{\partial J}{\partial z^{(2)}_1} \\ \vdots \\ \frac{\partial J}{\partial z^{(2)}_{n_2}} \end{pmatrix} \quad \quad \frac{\partial z^{(2)}}{\partial a^{(1)}_i} = \begin{pmatrix} \frac{\partial z^{(2)}_1}{\partial a^{(1)}_i} \\ \vdots \\ \frac{\partial z^{(2)}_{n_2}}{\partial a^{(1)}_i} \end{pmatrix} \]
Jetzt kann man das Skalarprodukt aus (d) wie folgt hinschreiben:
\[ \frac{\partial J}{\partial z^{(2)}} \frac{\partial z^{(2)}}{\partial a^{(1)}_i} = \sum_{p=1}^{n_2} \underbrace{\frac{\partial J}{\partial z^{(2)}_p}}_{\delta^{(2)}_p} \, \frac{\partial z^{(2)}_p}{\partial a^{(1)}_i} \]
Sie sehen es schon oben: Der linke Faktor ist das, was wir in Schritt 1 in (D1) als \(\delta^{(2)}_p\) definiert hatten. Schauen wir uns den rechten Faktor an und setzen dort die Formel (Z) für den Rohinput \(z^{(2)}_p\) ein:
\[ \frac{\partial z^{(2)}_p}{\partial a^{(1)}_i} = \frac{\partial}{\partial a^{(1)}_i} \left( \sum_{h=1}^{n_1} w^{(2)}_{p,h} \; a_h^{(1)} + b_p^{(1)} \right) = w^{(2)}_{p,i} \]
Unser Skalarprodukt sieht also wie folgt aus:
\[\tag{1} \frac{\partial J}{\partial z^{(2)}} \frac{\partial z^{(2)}}{\partial a^{(1)}_i} = \sum_{p=1}^{n_2} w^{(2)}_{p,i}\, \delta^{(2)}_p \]
Zu (2):
Wie schon in Schritt 1 ist dieser Term einfach die Ableitung der Aktivierungsfunktion \(g\). Das kann z.B. die logistische Funktion oder ReLU sein.
\[ \tag{2} \frac{\partial a_i^{(1)}}{\partial z^{(1)}_i} = \frac{\partial}{\partial z^{(1)}_i} g(z^{(1)}_i) = g'(z^{(1)}_i) \]
In diesem Fall lassen wir das \(g'\) stehen und lösen dies nicht weiter auf, so dass die Lösung unabhängig von der konkreten Aktivierungsfunktion bleibt.
Zu (3):
Wie in Schritt 1 setzen wir die Formel für \(z^{(2)}_i\) ein und lösen auf.
\[ \tag{3} \frac{\partial z^{(1)}_i}{\partial w^{(1)}_{i,j}} = \frac{\partial }{\partial w^{(1)}_{i,j}} \left( \sum_{p=1}^{n_0} w^{(1)}_{i,p} \; a_p^{(0)} + b_p^{(1)}\right) = a_j^{(0)} \]
Wir führen jetzt die Einzelergebnisse (1), (2), und (3) zusammen, indem wir sie in (d) einsetzen:
\[ \begin{align} \frac{\partial J}{\partial w^{(1)}_{i,j}} &= \underbrace{ \underbrace{\frac{\partial J}{\partial z^{(2)}} \frac{\partial z^{(2)}}{\partial a^{(1)}_i}}_{(1)} \quad \underbrace{\frac{\partial a^{(1)}_i}{\partial z^{(1)}_i}}_{(2)} }_{\frac{\partial J}{\partial z_i^{(1)}}} \quad \underbrace{\frac{\partial z^{(1)}_i}{\partial w^{(1)}_{i,j}}}_{(3)} \\[4mm] \tag{e} &= \left[ \sum_{p=1}^{n_2} \delta^{(2)}_p \, w^{(2)}_{p,i} \right] \quad g'(z^{(1)}_i) \quad a_j^{(0)} \end{align} \]
8.4.5 Fehlerterm \(\delta\)
Wir definieren jetzt wie schon bei Schritt 1 (D1) den Fehlerterm \(\delta\) als Ableitung von \(J\) nach \(z\) (das sind die Teile (1) und (2) oben zusammengenommen):
\[\tag{D2} \delta^{(1)}_i := \frac{\partial J}{\partial z_i^{(1)}} \]
Wie wir in der Zeile über (e) sehen, besteht dieses Delta aus den Teilen (1) und (2), d.h.:
\[ \tag{f} \delta^{(1)}_i = g'(z^{(1)}_i) \sum_{p=1}^{n_2} w^{(2)}_{p,i}\, \delta^{(2)}_p \]
Jetzt können wir die Ableitung von \(J\) in (e) also mit dem Delta jetzt so darstellen:
\[\tag{g}\frac{\partial J}{\partial w^{(1)}_{i,j}} = a_j^{(0)}\, \delta^{(1)}_i \]
8.4.6 Verallgemeinerung (D2, W)
Wir verallgemeinern wieder die Gleichungen (f) und (g) für Delta und Ableitung. Wir stellen uns vor, das Gewicht tritt an einer beliebigen Schicht \(l\) auf, wobei dieses \(l\) nicht die Schicht direkt vor der Ausgabeschicht ist, d.h. \(l\in\{1,\ldots,L-2\}\).
Dann können wir allgemein formulieren:
\[ \begin{align} \tag{D2}\delta^{(l)}_i &= g'(z^{(l)}_i) \sum_{p=1}^{n_{l+1}} w^{(l+1)}_{p,i}\, \delta^{(l+1)}_p \\[3mm] \tag{W''}\frac{\partial J}{\partial w^{(l)}_{i,j}} &= a_j^{(l-1)}\, \delta^{(l)}_i \end{align} \]
Wir haben somit (D2) hergeleitet und (W) jetzt auch für alle Schichten \(l\) hergeleitet (W’ und W’’ zusammen genommen).
8.5 Bias-Neuronen
Wir wenden die obige Herleitung jetzt auf die Gewichte der Bias-Neuronen an (B). Wir müssen hier nicht unterscheiden, ob wir in der Ausgabeschicht sind. Sehen wir uns also die Situation zwischen Eingabeschicht und Schicht 1 an.
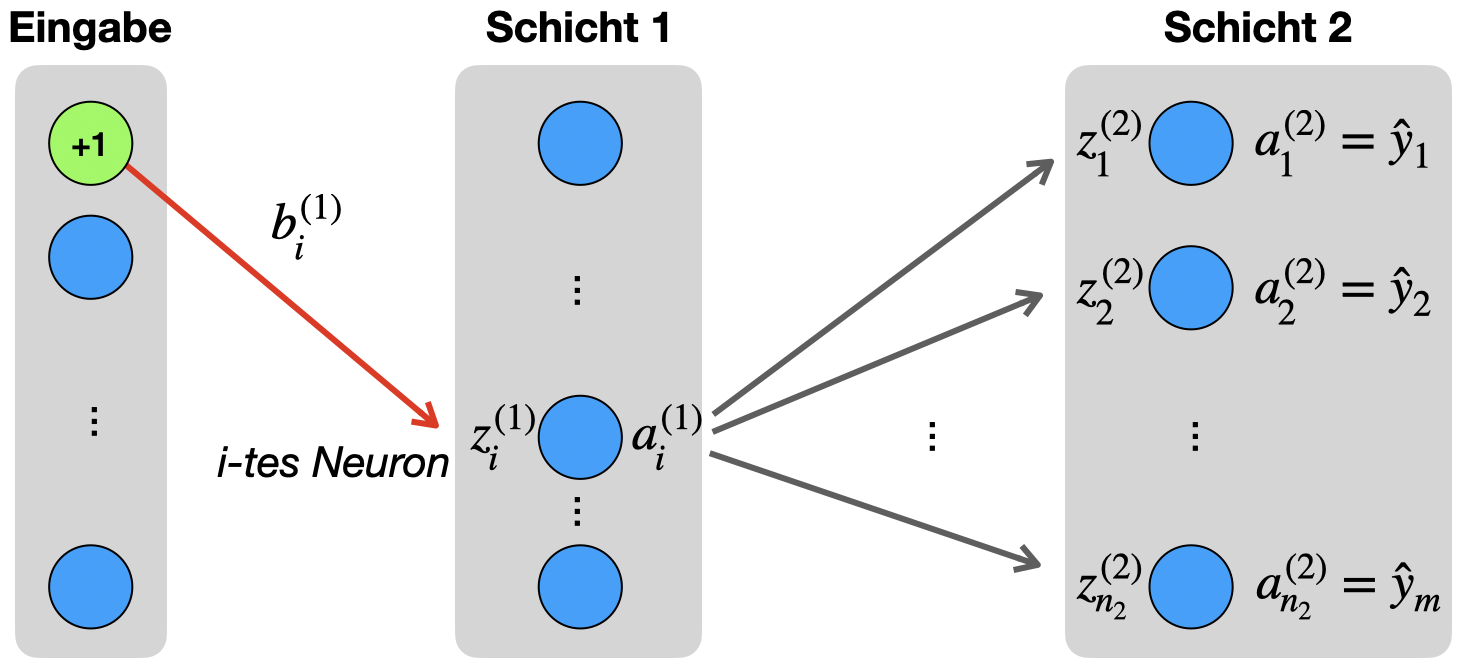
Wir wenden auch hier wieder die Kettenregel schrittweise an.
\[ \frac{\partial J}{\partial b^{(1)}_i} = \frac{\partial J}{\partial z^{(1)}_i} \frac{\partial z^{(1)}_i}{\partial b^{(1)}_i}\]
Wir bilden den Einfluss auf \(a^{(1)}_i\) ab:
\[ \frac{\partial J}{\partial b^{(1)}_i} = \frac{\partial J}{\partial a^{(1)}_i} \frac{\partial a^{(1)}_i}{\partial z^{(1)}_i}\frac{\partial z^{(1)}_i}{\partial b^{(1)}_i}\]
Der nächste Schritt sind wieder die grauen Pfeile rechts, also der Einfluss auf alle Rohinputs \(z^{(2)}_p\) der Schicht 2.
\[ \frac{\partial J}{\partial b^{(1)}_i} = \underbrace{\frac{\partial J}{\partial z^{(2)}} \frac{\partial z^{(2)}}{\partial a^{(1)}_i}}_1 \quad \underbrace{\frac{\partial a^{(1)}_i}{\partial z^{(1)}_i}}_2 \quad \underbrace{\frac{\partial z^{(1)}_i}{\partial b^{(1)}_i}}_3 \]
Tatsächlich unterscheiden sich die Rechnungen 1 und 2 nicht von der obigen Herleitung zu den Gewichten.
Einen Unterschied gibt es aber in 3: Wir setzen wir die Formel (Z) für \(z^{(1)}_i\) ein und lösen auf.
\[ \frac{\partial z^{(1)}_i}{\partial b^{(1)}_i} = \frac{\partial }{\partial b^{(1)}_i} \left( \sum_{p=1}^{n_1} w^{(1)}_{i,p} \; a_p^{(1)} + b_p^{(1)}\right) = 1 \]
Wir führen jetzt die Einzelergebnisse 1, 2, und 3 wieder zusammen:
\[ \begin{align} \frac{\partial J}{\partial b^{(1)}_i} &= \underbrace{\frac{\partial J}{\partial z^{(2)}} \frac{\partial z^{(2)}}{\partial a^{(1)}_i}}_1 \quad \underbrace{\frac{\partial a^{(1)}_i}{\partial z^{(1)}_i}}_2 \quad \underbrace{\frac{\partial z^{(1)}_i}{\partial b^{(1)}_i}}_3 \\[4mm] &= \left[ \sum_{p=1}^{n_3} \delta^{(2)}_p \, w^{(2)}_{p,i} \right] \quad g'(z^{(1)}_i) \quad 1 \end{align} \]
Unser Delta ist laut (D2) wie folgt definiert:
\[ \delta^{(1)}_i = g'(z^{(1)}_i) \sum_{p=1}^{n_2} w^{(1)}_{p,i}\, \delta^{(2)}_p \]
Wir setzen ein und bekommen:
\[ \frac{\partial J}{\partial b^{(1)}_i} = \delta^{(1)}_i \]
Wir verallgemeinern wieder und stellen uns vor, das Bias-Gewicht tritt an einer beliebigen Schicht \(l\in\{1,\ldots,L\}\) auf:
\[ \frac{\partial J}{\partial b^{(l)}_i} = \delta^{(l)}_i \]
Somit haben wir auch (B) hergeleitet.
8.6 Missing Pieces
8.6.1 Fehler über alle Trainingsbeispiele
Betrachten wir den Fehler an einer Zwischenschicht:
\[ \begin{align} \tag{D2}\delta^{(l)}_i &= g'(z^{(l)}_i) \sum_{p=1}^{n_{l+1}} w^{(l+1)}_{p,i}\, \delta^{(l+1)}_p \\[3mm] \tag{W}\frac{\partial J}{\partial w^{(l)}_{i,j}} &= a_j^{(l-1)}\, \delta^{(l)}_i \end{align} \]
Wir haben bislang immer nur den Fehler für ein Trainingsbeispiel \(k\) betrachtet, d.h. eigentlich müsste (W) so heißen:
\[ \frac{\partial J_k}{\partial w^{(l)}_{i,j}} = a_j^{(l-1)}\, \delta^{(l)}_i \]
Der Zusammenhang zwischen dem Fehler \(J_k\) für ein einziges Trainingsbeispiel und dem Gesamtfehler \(J\) ist:
\[ J = \frac{1}{N} \sum_{k=1}^N J_k \]
Wenn wir jetzt (J2) verwenden, um alle Trainingsbeispiele zu berücksichtigen, dann wird die Ableitung für ein Gewicht wie folgt:
\[ \begin{align*} \frac{\partial J}{\partial w^{(l)}_{i,j}} &= \frac{\partial }{\partial w^{(l)}_{i,j}} \frac{1}{N} \sum_{k=1}^N J_k \\[4mm] &= \frac{1}{N} \sum_{k=1}^N \frac{\partial J_k}{\partial w^{(l)}_{i,j}} \end{align*} \]
Was man hoffentlich klar sehen kann: Die Ableitung kann ohne weiteres in die Summe hineingezogen werden. Das bedeutet, dass man Backpropagation so verwenden kann, dass man alle Trainingsbeispiele durchläuft, bevor man ein Update durchführt. Dazu berechnet man die einzelnen \(\Delta w\) für jedes Tainingsbeispiel und mittelt am Ende einer Epoche.
Genauso besagt der Zusammenhang oben, dass man Mini-Batch durchführen kann (siehe Abschnitt 4.2.6). Das heißt, man nimmt eine Teilmenge der Trainingsdaten, berechnet die einzelnen \(\Delta w\) nur für diese Daten und mittelt nur über diese Menge.
8.6.2 Regularisierung
Bei unserer Fehlerfunktion \(J\) haben wir den Regularisierungsterm weggelassen (siehe Abschnitt 4.2.2). Mit Regularisierung sieht unsere Verlustfunktion \(J_\text{reg}\) so aus:
\[ J_\text{reg} = J + \frac{\lambda}{2} \sum_{l=1}^{L} \left\Vert W^{(l)} \right\Vert^2 \]
Im letzten Kapitel haben wir in Abschnitt 4.2.2 gezeigt, dass dieser Summand bei der Ableitung aber nur dahingehend eine Rolle spielt, dass er das ursprüngliche Gewicht \(w^{(l)}_{i,j}\) um einen bestimmten Betrag reduziert (weight decay). Man müsste dies bei einer Implementierung natürlich berücksichtigen und die Backpropagation-Formeln entsprechend anpassen.