5  Einführung in Keras

Im praktischen Teil werden wir hauptsächlich mit Keras - innerhalb von TensorFlow - arbeiten. Wir lernen, wie man Feedforward-Netze in Keras erstellt, trainiert und evaluiert. Wir starten mit den Iris-Daten und einem sehr einfachen Netz. Dann lernen wir die MNIST-Daten zur Erkennung von handgeschriebenen Ziffern kennen und erstellen und trainieren ein FFN mit mehreren Schichten.

Lernziele, um Ihren Lernfortschritt zu prüfen

Nach Abschluss des Kapitels können Sie

• die Begriffe und Unterschiede von TensorFlow, Keras und PyTorch erklären
• Feedforwardnetze in Python mit Hilfe der Keras-Bibliothek erstellen, mit Daten aus Keras trainieren und den Trainingsverlauf visualisieren
• den MNIST-Datensatz beschreiben und das Training in Keras verwenden
• verschiedene Hyperparameter (Lernrate, Batchgröße etc.) benennen und ihre Bedeutung in konkreten Trainingssituationen beurteilen

Updates dieser Seite

• 05.05.2025: Sparse categorical crossentropy - Erklärung hinzugefügt
• 02.05.2025: kleine Codeanpassungen (z.B. Initializer raus, binary_crossentropy)
• 10.04.2025: Kapitel umstrukturiert

Datensatz

Name	Daten	Anz. Klassen	Klassen	Trainings-/Testdaten	Ort
Iris	Blütenblatt-Maße	3	Blumenklassen	150
MNIST	s/w-Bilder (28x28)	10	handgeschriebene Ziffern 0…9	60000/10000	5.4

Importe

import tensorflow
import math
from math import exp
import matplotlib.pyplot as plt
import numpy as np
import time

5.1 Hintergrund

5.1.1 TensorFlow

TensorFlow ist eine Open-Source-Bibliothek für Python (mit Bestandteilen in C++) für den Themenbereich des Maschinellen Lernens, inklusive Neuronaler Netze. TensorFlow wurde ursprünglich vom Google Brain Team für Google-eigenen Projekte entwickelt, wurde aber 2015 unter einer Open-Source-Lizenz (Apache License 2.0) für die Allgemeinheit frei gegeben. Mittlerweile dürfte TensorFlow das mit Abstand das wichtigste Framework im Bereich Maschinelles Lernen sein.

Noch ein paar Worte zum Entwicklungsteam hinter TensorFlow: Google Brain begann 2011 als ein sogenanntes “Google X”-Projekt als Kooperation zwischen Google-Fellow Jeff Dean und Stanford-Professor Andrew Ng. Seit 2013 ist Deep-Learning-Pioneer Geoffrey Hinton als leitender Wissenschaftler im Team. Weitere bekannte Wissenschaftler bei Google Brain sind Alex Krizhevsky und Ilya Sutskever (Autoren von AlexNet), Christopher Olah (bekannt durch seinen Blog) und Chris Lattner (Erfinder von Apple’s Programmiersprache Swift).

5.1.2 Keras

Keras ist ebenfalls eine Open-Source-Bibliothek für Python von François Chollet, die erstmals 2015 als Python-API für verschiedene “Backends” (u.a. TensorFlow) veröffentlicht wurde. Es ist ein objektorientiertes Framework für das Erstellen, Trainieren und Evaluieren Neuronaler Netze. Das Buch Deep Learning with Python (Chollet 2021) ist vom Erfinder von Keras und daher von besonderer Relevanz (einschränkend muss man sagen, dass die Theorie in dem Buch ein wenig zu kurz kommt). Eine Idee von Keras ist, dass es auch als Interface für verschiedene Backends in anderen Kontexten (z.B. Robotik oder mobile) genutzt werden kann. Daher liegt ein Fokus von Keras auf einer intuitiven, modularen und erweiterbaren Systematik.

Keras wurde unabhängig von TensorFlow entwickelt, wurde dann aber 2017 in TensorFlow 1.4 als Teil der TensorFlow Core API aufgenommen, d.h. alle Konzepte und Daten von Keras stehen in TensorFlow zur Verfügung. François Chollet arbeitet seit 2015 für Google und hat dort auch die Einbindung in TensorFlow unterstützt.

5.1.3 PyTorch

PyTorch ist - wie TensorFlow - eine Open-Source-Bibliothek für Maschinelles Lernen in Python. PyTorch wurde ursprünglich von der KI-Gruppe bei Facebook, genannt FAIR - Facebook AI Research (oder oft nur “Facebook AI”) - entwickelt. PyTorch ist in letzter Zeit immer populärer geworden, weil es an manchen Stellen einen direkteren Eingriff in die Abläufe zulässt. In diesem Buch wird hauptsächlich Keras verwendet, aber PyTorch wird in den Anhängen E und F zumindest angerissen.

5.2 Einfaches Neuronales Netz

Wir beginnen mit dem einfachsten möglichen Neuronales Netz und lernen, wie wir es erzeugen und trainieren (wir verzichten auf Testdaten).

In Keras heißt die Basisklasse für Neuronale Netze Sequential. Der Name weist darauf hin, dass ein Sequential-Objekt eine geordnete Reihe (Sequenz) von Schichten enthält.

Wir erstellen zunächst ein Neuronales Netz mit einer Schicht. Also stellen wir eine Instanz von Sequential her, dies wäre unser Modell.

from tensorflow.keras.models import Sequential

model = Sequential()

5.2.1 Schichten Input und Dense

Jetzt kann man Schichten als Objekte dem Modell hinzufügen. Es gibt verschiedene Arten von Schichten.

Als erstes fügen wir die Neuronen für die Eingabe als Objekt der Klasse Input hinzu. Diese “Schicht” hat keine Parameter, die zu lernen sind, und wird daher nicht als Schicht gezählt.

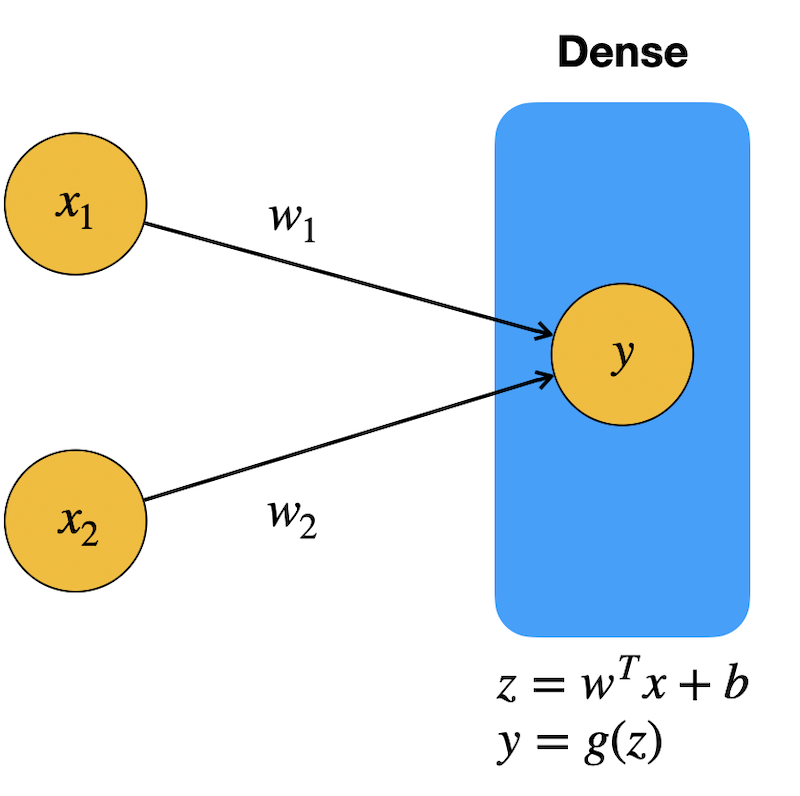
Unsere erste “richtige” Schicht ist ein Objekt vom Typ Dense. Diese Schicht verbindet sich mit allen Neuronen der Vorgängerschicht. In anderen Kontexten nennt man solche Schichten auch fully connected layer oder FC layer. Unsere Dense-Schicht ist gleichzeitig auch die Ausgabeschicht und hat daher nur ein Neuron (der erste Parameter).

Mit activation kann man die Aktivierungsfunktion spezifizieren. Wir wählen die Funktion sigmoid, also die logistische Funktion:

\[ g(z) = \frac{1}{1-e^{-z}} \]

Dies ist die typische Aktivierung für das Ausgabeneuron bei binärer Klassifikation.

from tensorflow.keras import Input
from tensorflow.keras.layers import Dense

model = Sequential()
model.add(Input(shape=(2,)))           # Zwei Eingabeneuronen
model.add(Dense(1,                     # Ein (Ausgabe-)Neuron in dieser Schicht
                activation='sigmoid')) # Aktivierungsfunktion am Ausgabeneuron

Unser Netz sieht derzeit so aus (das Bias-Neuron ist nicht grafisch repräsentiert):

Mit der Methode summary geben wir uns eine Zusammenfassung unserer Netzwerk-Architektur aus, was später bei komplexeren Netzen hilfreich ist.

model.summary()

Model: "sequential_1"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ dense (Dense)                   │ (None, 1)              │             3 │
└─────────────────────────────────┴────────────────────────┴───────────────┘

 Total params: 3 (12.00 B)

 Trainable params: 3 (12.00 B)

 Non-trainable params: 0 (0.00 B)

Wir haben drei Parameter: \(w_1\), \(w_2\) und \(b\).

5.2.2 Parameter

Man kann das Netzwerkobjekt auch programmatisch untersuchen. Die Eigenschaft layers enthält alle Schichtenobjekte in iterierbarer Form. Hier wenden wir die Methode get_config auf jede Schicht an, die uns ein Dictionary zurückgibt, das wir hier ausgeben.

for l in model.layers:
    for key in l.get_config():
        print(f'{key}: {l.get_config()[key]}')

name: dense
trainable: True
dtype: {'module': 'keras', 'class_name': 'DTypePolicy', 'config': {'name': 'float32'}, 'registered_name': None}
units: 1
activation: sigmoid
use_bias: True
kernel_initializer: {'module': 'keras.initializers', 'class_name': 'GlorotUniform', 'config': {'seed': None}, 'registered_name': None}
bias_initializer: {'module': 'keras.initializers', 'class_name': 'Zeros', 'config': {}, 'registered_name': None}
kernel_regularizer: None
bias_regularizer: None
kernel_constraint: None
bias_constraint: None

Besonders interessant sind natürlich die Gewichte, zumindest bei kleineren Netzen (später werden die Gewichte nicht mehr handhabbar).

Mit der Methode get_weights kann man sich die Gewichte und Bias-Gewichte aller Schichten ausgeben lassen.

w, b = model.get_weights()
print(f'WEIGHTS {w[0]} {w[1]} BIAS {b}')

WEIGHTS [-1.058739] [-0.54168177] BIAS [0.]

Man sieht, dass die Gewichte auf Zufallswerte in einer bestimmten Wertespanne gesetzt werden. Unter Layer weight initializers finden Sie Infos zu den unterschiedlichen Methoden zur zufälligen Initialisierung der Gewichte.

5.2.3 Iris-Datensatz

Wenn Sie nicht genau wissen, was ein “Tensor” ist oder wie man mit Vektoren, Matrizen und Tensoren in Python/NumPy umgeht, sehen Sie sich Abschnitt 1.1.4 an.

Wir möchten jetzt noch das Experiment mit den Iris-Daten aus Kapitel 3 mit einem Keras-Netz wiederholen. Wir bereiten die Daten wieder für eine binäre Klassifikation vor, dass wir nur zwei Features haben und nur zwei Klassen; wie im Abschnitt 3.4.1.

Wir arbeiten hier nur mit Trainingsdaten und verzichten auf eine Trennung ist Test- und Trainingsdaten.

from sklearn import datasets

iris = datasets.load_iris()

Wir reduzieren die Features auf zwei Features.

Wir zeigen hier einen alternativen Weg, die Spalten 0 und 2 auszuwählen (und die anderen zu ignorieren). Der Doppelpunkt bei

iris.data[:, [0, 2]]

bedeutet, dass alle Zeilen ausgewählt werden.

x_iris = iris.data[:, [0, 2]]
x_iris[:5] # Testausgabe

array([[5.1, 1.4],
       [4.9, 1.4],
       [4.7, 1.3],
       [4.6, 1.5],
       [5. , 1.4]])

Wir reduzieren die Daten auf zwei Klassen, indem wir nur die vorderen 100 von den 150 Beispielen nehmen:

x_iris = x_iris[:100] # nur die ersten 100 Elemente (also zwei Klassen)
y_iris = iris.target[:100]
y_iris

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])

Jetzt schauen wir uns die Daten nochmal an:

plt.scatter(x_iris[:50, 0], x_iris[:50, 1], color='red', marker='o', label='setosa')
plt.scatter(x_iris[50:, 0], x_iris[50:, 1], color='blue', marker='x', label='versicolor')
plt.xlabel('sepal length')
plt.ylabel('petal length')
plt.legend(loc='upper left')
plt.show()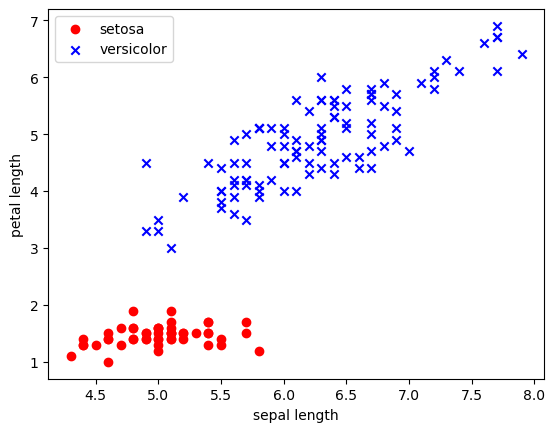

5.2.4 Training

Wir trainieren das Netzwerk mit Backpropagation in 10 Epochen. Wir haben keine Testdaten, sondern lediglich einen Trainingsdatensatz mit 100 Beispielen. Damit man ein Keras-Netzwerk trainieren kann, muss es zunächst mit der Methode compile konfiguriert werden.

Konfiguration mit Compile

Mit compile legen wir Hyperparameter wie die Lernrate und die Optimierungsmethode fest, aber auch Metriken wie die Art der Zielfunktion und die Evaluationsmaße.

Wir verwenden hier stochastic gradient descent (SGD) als Optimierungsmethode, mit einer Lernrate von 0.1. Als Zielfunktion wählen wir MSE (gemittelte Fehlerquadrate) und als Evaluationsmaß Accuracy (dazu mehr im nächsten Kapitel, Abschnitt 6.2.9).

from tensorflow.keras.optimizers import SGD

sgd = SGD(learning_rate=0.1)

model.compile(optimizer=sgd, 
              loss='binary_crossentropy', 
              metrics=['acc'])

# Alternative:
# Hier benötigt man das Objekt in sgd nicht, kann allerdings auch
# nicht die Lernrate einstellen
#
# model_and.compile(optimizer='sgd', loss='binary_crossentropy', metrics=['acc'])

Hinweis

Wie wir später noch sehen, muss man nicht unbedingt ein Objekt für den Optimizer herstellen, sondern kann auch einfach in der Methode compile optimizer=‘sgd’ angeben. Das Vorgehen hier benötigt man nur, wenn man den Optimizer konfigurieren will (wie hier mit der Lernrate).

Training mit Lernrate 0.1

Das eigentliche Training, also die Updates der Paramter mit Hilfe der Trainingsdaten, findet in der Methode fit statt. Hier geben wir die Featurevektoren an, die Zielwerte und die Anzahl der Epochen, also die Trainingsdauer.

history = model.fit(x_iris, 
                    y_iris, 
                    epochs=10)

Epoch 1/10

1/4 ━━━━━━━━━━━━━━━━━━━━ 1s 446ms/step - acc: 0.3750 - loss: 5.2872

4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - acc: 0.4625 - loss: 3.6283  

Epoch 2/10

1/4 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step - acc: 0.9688 - loss: 0.6038

4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - acc: 0.8719 - loss: 0.6046 

Epoch 3/10

1/4 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - acc: 1.0000 - loss: 0.4855

4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - acc: 0.8499 - loss: 0.4894 

Epoch 4/10

1/4 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step - acc: 0.6250 - loss: 0.5954

4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - acc: 0.7686 - loss: 0.5391 

Epoch 5/10

1/4 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - acc: 0.5000 - loss: 0.5729

4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - acc: 0.7527 - loss: 0.4784 

Epoch 6/10

1/4 ━━━━━━━━━━━━━━━━━━━━ 0s 14ms/step - acc: 0.9688 - loss: 0.3438

4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - acc: 0.9753 - loss: 0.3522 

Epoch 7/10

1/4 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step - acc: 1.0000 - loss: 0.3081

4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - acc: 1.0000 - loss: 0.3168 

Epoch 8/10

1/4 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - acc: 0.9688 - loss: 0.3646

4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - acc: 0.9845 - loss: 0.3214 

Epoch 9/10

1/4 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step - acc: 0.9688 - loss: 0.2891

4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - acc: 0.9845 - loss: 0.2769 

Epoch 10/10

1/4 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - acc: 1.0000 - loss: 0.2728

4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - acc: 1.0000 - loss: 0.2576 

Ergebnis

Wir sehen uns die Entwicklung von Loss und Accuracy an.

Dazu definieren wir eine Hilfsfunktion:

def plot_loss_acc(history):
    epochs = range(len(history.history['acc']))
    fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(10,4))
    ax[0].plot(epochs, history.history['loss'], 'r', label='Loss')
    ax[0].set_xlabel('Epochen')
    ax[0].set_ylabel('Loss')
    ax[0].set_title('Loss')
    ax[1].plot(epochs, history.history['acc'], 'b', label='Accuracy')
    ax[1].set_xlabel('Epochen')
    ax[1].set_ylabel('Accuracy')
    ax[1].set_title('Accuracy')
    plt.show()

plot_loss_acc(history)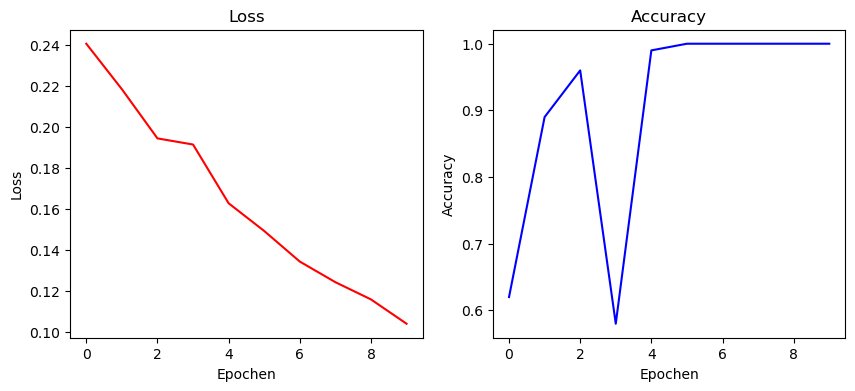

Man sieht hier, dass das Netz mit Lernrate 0.1 bereits nach 5 Epochen 100% Accuracy erreicht.

Wir können uns noch die Gewichte ausgeben:

w, b = model.get_weights()
print(f'WEIGHTS {w[0]} {w[1]} BIAS {b}')

WEIGHTS [-0.6526667] [1.1560209] BIAS [-0.0362203]

5.2.5 Vorhersage

Man kann mit predict auch Vorhersagen mit dem trainierten Netz berechnen. Hier für 10 Werte aus der ersten Hälfte der 100 Datenpunkte (Klasse 0):

pred = model.predict(x_iris[:10])
pred

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step

array([[0.14850295],
       [0.16577686],
       [0.16785213],
       [0.2134161 ],
       [0.1569466 ],
       [0.16862759],
       [0.19465251],
       [0.17285565],
       [0.21593328],
       [0.18238737]], dtype=float32)

Da wir kontinuierliche Werte bekommen, legen wir eine Schwellwertfunktion an, um die Ausgabe auf die Werte {0, 1} zu zwingen.

[(1 if x>=0.5 else 0) for x in pred]

[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

Hier für Werte aus der “Mitte” der Daten (40 bis 59), wo die eine Hälfte noch zu Klasse 0 gehört, die andere zu Klasse 1.

pred = model.predict(x_iris[40:60])
[(1 if x>=0.5 else 0) for x in pred]

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 15ms/step

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step

[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]

5.3 Feedforward-Netze

Unser erstes Netz hatte lediglich eine parametrisierte Schicht und ein Ausgabeneuron.

Jetzt sehen wir uns an, wie man FNN mit Zwischenschichten erstellt, das für die Klassifikation von 10 Klassen geeignet ist.

5.3.1 Verlustfunktion in Keras

Bevor man ein Modell in Keras mit fit trainiert, legt man mit compile die Verlustfunktion fest (siehe dazu auch Abschnitt 4.2.1), z.B. so:

model.compile(loss='categorical_crossenropy', optimizer='sgd')

Die Loss-Funktion ist in der Regel eine von diesen (die Begiffe sind mit der Keras-Dokumentation verlinkt):

• binary_crossentropy
• categorical_crossentropy
• sparse_categorical_crossentropy

Hier nochmal eine kurze Erklärung, wann Sie welche nehmen:

Sie verwenden binary_crossentropy für binäre Klassifikation, wo Ihre Labels als Liste mit Nullen und Einsen vorliegen.

Auf categorical_crossentropy greifen Sie bei der Klassifikation mit multiplen Klassen zurück (Beispiel MNIST mit Klassen 0 bis 9). Hier müssen die Labels in One-Hot-Encoding vorliegen.

Die sparse_categorical_crossentropy verwenden Sie ebenfalls bei der Klassifikation mit multiplen Klassen, aber hier liegen die Labels als Integer-Werte vor, also z.B. [1, 5, 3, 0] etc.

Wir wandeln die Labels in One-Hot-Encoding um und verwenden dann categorical_crossentropy.

Wie funktioniert sparse_categorical_crossentropy?

Nehmen wir an, dass wir 10 Klassen haben wie bei MNIST. In unseren Daten liegen die y-Werte als Zahlen zwischen 0 und 9 vor. Für categorical_crossentropy müssen wir diese y-Werte in Vektoren der Länge 10 umwandeln. Warum eigentlich? Wir brauchen die Vektorform für die Berechnung der Verlustfunktion (hier für ein Trainingsbeispiel):

\[ J = - \sum_{i=1}^m y_i\, log(\hat{y}_i) \]

Nehmen wir ein konkretes Beispiel: Wir haben ein Trainingsbeispiel, wo \(p \in {0,\ldots,9}\) der Zielwert ist (z.B. 5) und \(y\) der entsprechende One-Hot-Vektor der Länge 10 mit einer 1 an Position \(p\) (sonst 0). Dann ist der Verlust für dieses Trainingsbeispiel:

\[ J = - log(\hat{y}_p) \]

Es bleibt also nur der Summand mit dem Index \(p\) übrig. Dieser Index stand aber doch in den ursprünglichen y-Werte drin. Bei sparse_categorical_crossentropy berechnet man daher einfach den Verlust mit Hilfe des \(p\), ohne die Summe zu verwenden, wo im Grunde der One-Hot-Vektor nur als “Selektor” gebraucht wird. Ganz einfach also. Es handelt sich nicht um eine andere Berechnung, sondern um eine “Abkürzung”.

5.4 MNIST-Datensatz

MNIST kurz gefasst

Im MNIST-Datensatz geht es Erkennung von handgeschriebenen Ziffern von 0 bis 9. Es gibt zehn Klassen, die es vorherzusagen gilt: 0, 1, 2, … 9. Die Bilder haben die Auflösung 28x28 und liegen in Graustufen vor. Der Datensatz enthält 60000 Trainingsbeispiele und 10000 Testbeispiele.

Wir ziehen den Datensatz MNIST hinzu. MNIST steht für Modified National Institute of Standards and Technology (dataset). Siehe auch den Wikipedia-Artikel zu MNIST und die Keras-Doku zu MNIST.

Eine Einführung in die MNIST-Daten in Keras finden Sie im folgenden Video.

5.4.1 Daten einlesen

Die Daten kommen bereits separiert in Trainings- und Testdaten.

from tensorflow.keras.datasets import mnist

(x_train, y_train), (x_test, y_test) = mnist.load_data()

Wir sehen uns die Struktur an. Die Bilder sind als 28x28-Matrizen hinterlegt.

print('x_train: ', x_train.shape)
print('y_train: ', y_train.shape)
print('x_test: ', x_test.shape)
print('y_test: ', y_test.shape)

x_train:  (60000, 28, 28)
y_train:  (60000,)
x_test:  (10000, 28, 28)
y_test:  (10000,)

5.4.2 Daten visualisieren

Die Funktion imshow (image show) erlaubt uns das schnelle Betrachten der Bilder. Wir wählen als color map (cmap) Graustufen.

Erstes Trainingsbild:

plt.imshow(x_train[0], cmap='gray')

<matplotlib.image.AxesImage at 0x150dd31d0>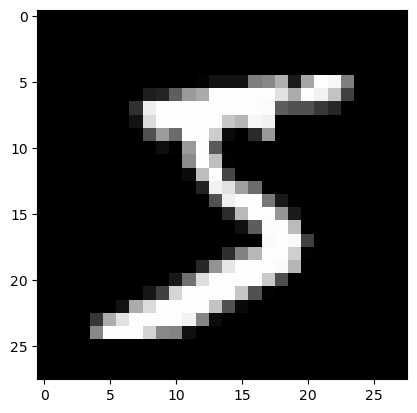

Zehntes Trainingsbild:

plt.imshow(x_train[9], cmap='gray')

<matplotlib.image.AxesImage at 0x151ba3110>

Hier geben wir von jeder Kategorie das erste Trainingsbeispiel aus:

fig, ax = plt.subplots(nrows=2, ncols=5, sharex=True, sharey=True,)
ax = ax.flatten() 
for i in range(10):
    img = x_train[y_train == i][0]
    ax[i].imshow(img, cmap='gray')

ax[0].set_xticks([]) # keine Achsenmarkierungen
ax[0].set_yticks([])
plt.tight_layout()
plt.show()

5.4.3 Daten vorverarbeiten

Für unsere Zwecke möchten wir die Bildmatrizen linearisieren zu Vektoren der Länge 784 (= 28*28). Dazu verwenden wir reshape.

Außerdem möchten wir die Pixelwerte (0..255) auf das Interval [0, 1] normalisieren. Das erreichen wir, indem wir alle Werte durch 255.0 teilen.

x_train = x_train.reshape(60000, 784)/255.0
x_test = x_test.reshape(10000, 784)/255.0

Kleiner Check, ob die Linearisierung geklappt hat:

print('x_train: ', x_train.shape)
print('x_test: ', x_test.shape)

x_train:  (60000, 784)
x_test:  (10000, 784)

5.4.4 One-Hot Encoding

Um die zehn Ziffern 0, , 9 in der Ausgabe zu kodieren, benutzen wir One-Hot Encoding, d.h. jede Ziffer wird durch einen Vektor der Länge 10 repräsentiert:

\[ \left( \begin{array}{c} 1 \\0 \\ \vdots \\ 0\end{array} \right) \quad \left( \begin{array}{c} 0 \\1 \\ \vdots \\ 0\end{array} \right) \quad \ldots\quad \left( \begin{array}{c} 0 \\0 \\ \vdots \\ 1\end{array} \right) \]

In Keras gibt es dafür die Funktion to_categorical. Wir schreiben das Ergebnis in neue Variablen.

from tensorflow.keras.utils import to_categorical

y_train_1hot = to_categorical(y_train, 10)
y_test_1hot = to_categorical(y_test, 10)

Wir prüfen, ob die Label-Daten die richtige Form haben.

print("y_train: ", y_train_1hot.shape)
print("y_test: ", y_test_1hot.shape)

y_train:  (60000, 10)
y_test:  (10000, 10)

Das passt: Es sind Vektoren der Länge 10.

5.5 Netz mit zwei Schichten

Wir bauen jetzt ein Neuronales Netz mit einer “versteckten” Schicht (hidden layer) mit 60 Neuronen.

Das Netz benötigt für die MNIST-Daten eine Eingabeschicht mit 784 Neuronen und hat zwei parametrisierte Schichten:

• Versteckte Schicht mit 60 Neuronen
• Ausgabeschicht mit 10 Neuronen

Schematisch sieht das so aus (ohne Bias-Neuronen):

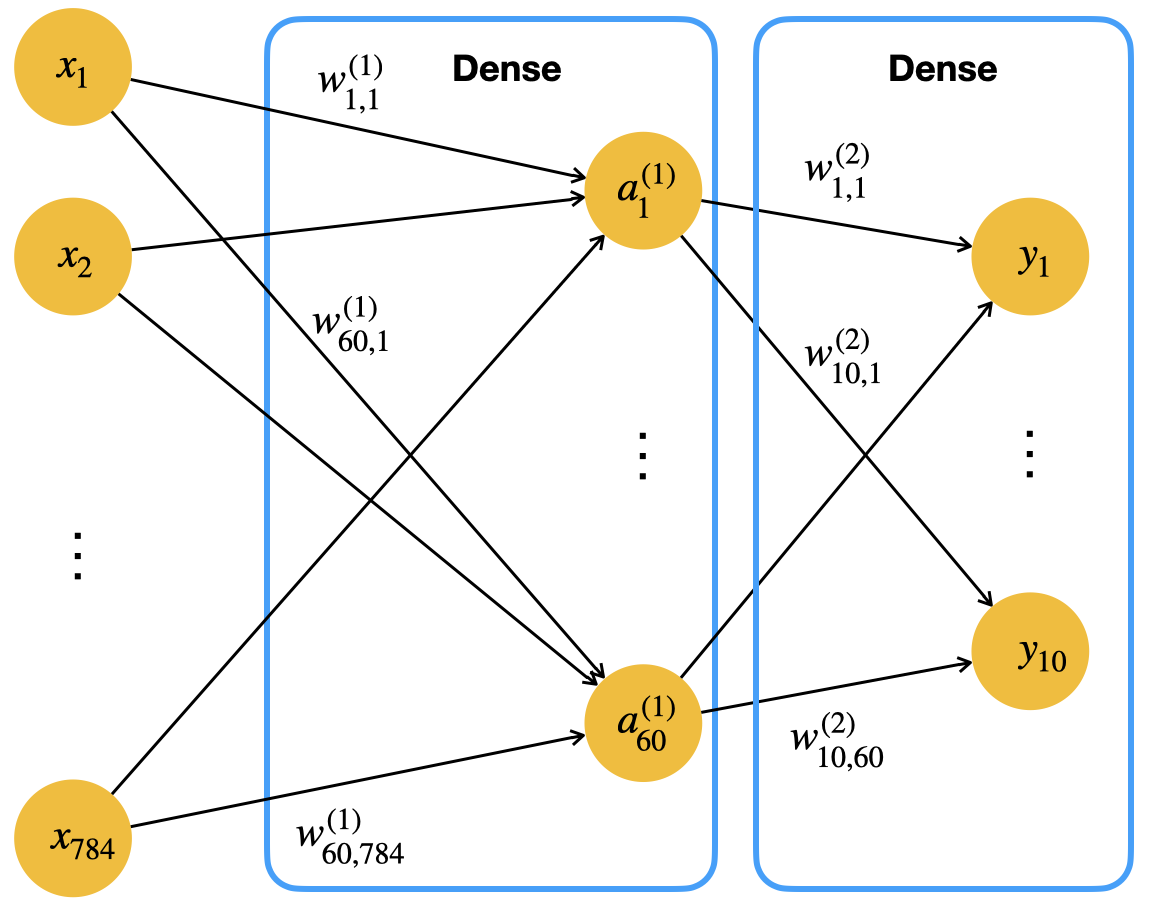
5.5.1 Modell

In Keras erstellen wir das Netz als Instanz der Klasse Sequential.

Neben der Eingabe fügen dem Objekt zwei parametrisierte Schichten vom Typ Dense (fully connected) hinzu. Wir wählen die Sigmoid-Funktion für die Aktivierung der versteckten Schicht. Bei der Ausgabeschicht geben wir an, dass wir die Softmax-Funktion anwenden möchten. Denken Sie daran, dass Sie bei Klassifikation mit drei und mehr Klassen immer Softmax an der Ausgabe verwenden müssen.

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Input, Dense

model = Sequential()
model.add(Input(shape=(784,)))
model.add(Dense(60, 
                activation='sigmoid'))
model.add(Dense(10,
                activation='softmax'))

5.5.2 Anzahl der Parameter

Wie viele Parameter hat das Netz? Die Gewichtsmatrix \(W^{(1)}\) von Input- zu versteckter Schicht hat 784x60 Einträge:

784*60

47040

Es kommen 60 Gewichte für das Bias-Neuron dazu. Insgesamt also 47100 Parameter. Die Gewichtsmatrix \(W^{(2)}\) von versteckter zu Ausgabeschicht enthält 10x60 = 600 Einträge plus den 10 Gewichten für das Bias-Neuron zur Ausgabe, macht 610 Parameter. Alles in allem also 47710 Parameter.

Wir schauen uns das Netz in der Kurzübersicht mit Hilfe der Methode summary an. Dort steht auch nochmal die Anzahl der Parameter:

model.summary()

Model: "sequential_2"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ dense_1 (Dense)                 │ (None, 60)             │        47,100 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_2 (Dense)                 │ (None, 10)             │           610 │
└─────────────────────────────────┴────────────────────────┴───────────────┘

 Total params: 47,710 (186.37 KB)

 Trainable params: 47,710 (186.37 KB)

 Non-trainable params: 0 (0.00 B)

Einen etwas technischeren Blick auf Ihr Modell mit allen Schichten erhalten Sie mit get_config. Hier sehen Sie zum Beispiel verschiedene Einstellungen in den Schichten, z.B. zur Initialisierung der Gewichte.

model.get_config()

{'name': 'sequential_2',
 'trainable': True,
 'dtype': {'module': 'keras',
  'class_name': 'DTypePolicy',
  'config': {'name': 'float32'},
  'registered_name': None},
 'layers': [{'module': 'keras.layers',
   'class_name': 'InputLayer',
   'config': {'batch_shape': (None, 784),
    'dtype': 'float32',
    'sparse': False,
    'ragged': False,
    'name': 'input_layer_1'},
   'registered_name': None},
  {'module': 'keras.layers',
   'class_name': 'Dense',
   'config': {'name': 'dense_1',
    'trainable': True,
    'dtype': {'module': 'keras',
     'class_name': 'DTypePolicy',
     'config': {'name': 'float32'},
     'registered_name': None},
    'units': 60,
    'activation': 'sigmoid',
    'use_bias': True,
    'kernel_initializer': {'module': 'keras.initializers',
     'class_name': 'GlorotUniform',
     'config': {'seed': None},
     'registered_name': None},
    'bias_initializer': {'module': 'keras.initializers',
     'class_name': 'Zeros',
     'config': {},
     'registered_name': None},
    'kernel_regularizer': None,
    'bias_regularizer': None,
    'kernel_constraint': None,
    'bias_constraint': None},
   'registered_name': None,
   'build_config': {'input_shape': (None, 784)}},
  {'module': 'keras.layers',
   'class_name': 'Dense',
   'config': {'name': 'dense_2',
    'trainable': True,
    'dtype': {'module': 'keras',
     'class_name': 'DTypePolicy',
     'config': {'name': 'float32'},
     'registered_name': None},
    'units': 10,
    'activation': 'softmax',
    'use_bias': True,
    'kernel_initializer': {'module': 'keras.initializers',
     'class_name': 'GlorotUniform',
     'config': {'seed': None},
     'registered_name': None},
    'bias_initializer': {'module': 'keras.initializers',
     'class_name': 'Zeros',
     'config': {},
     'registered_name': None},
    'kernel_regularizer': None,
    'bias_regularizer': None,
    'kernel_constraint': None,
    'bias_constraint': None},
   'registered_name': None,
   'build_config': {'input_shape': (None, 60)}}],
 'build_input_shape': (None, 784)}

5.5.3 Gewichtsmatrizen und Biasvektoren

Mit get_weights können wir auf die Parameter des Netzwerks zugreifen. Für jede Schicht gibt es jeweils

• eine Gewichtsmatrix und
• einen Bias-Vektor.

Wir lassen uns hier in einer Schleife jeweils die Dimensionen der Gewichtsmatrix und des Bias-Vektor für unsere zwei Schichten (Hidden + Output) ausgeben:

weights = model.get_weights()
for w in weights:
    print(w.shape)

(784, 60)
(60,)
(60, 10)
(10,)

Wir sehen hier, dass die Gewichtsmatrix \(W^{(1)}\) von der Eingabeschicht zur versteckten Schicht die Dimensionen 784x60 hat. In unserer theoretischen Behandlung haben wir eine 60x784-Matrix verwendet, also die transponierte Version. Beide Varianten sind möglich und üblich.

Der Bias-Vektor von Input zu Hidden hat eine Länge von 60. Auch das ist plausibel, wenn Sie sich in der Abbildung oben ein Bias-Neuron in der Inputschicht vorstellen, dass mit allen 60 versteckten Neuronen verbunden ist. Dies muss offensichtlich 60 Gewichte haben.

5.5.4 Training

Beim Training wollen wir die ursprüngliche Variante des Backpropagation verwenden, wo alle Trainingsbeispiele vor einem Update durchlaufen werden. Wir nennen diese Variante Batchtraining (nicht zu verwechseln mit “Minibatch”, siehe unten).

In Keras spezifizieren wir dazu Stochastic Gradient Descent, kurz SGD, als Optimierungsmethode und geben als Batchgröße die Anzahl der Trainingsdaten an. Als Zielfunktion wählen wir wie im Theorieteil die Cross-Entropy-Funktion.

Lernrate

Damit wir die Lernrate einstellen können, erstellen wir für die Optimierungsmethode ein eigenes SGD-Objekt (stochastic gradient descent). Wir sehen uns mit get_config die Voreinstellungen an.

from tensorflow.keras.optimizers import SGD

opt = SGD()
opt.get_config()

{'name': 'SGD',
 'learning_rate': 0.009999999776482582,
 'weight_decay': None,
 'clipnorm': None,
 'global_clipnorm': None,
 'clipvalue': None,
 'use_ema': False,
 'ema_momentum': 0.99,
 'ema_overwrite_frequency': None,
 'loss_scale_factor': None,
 'gradient_accumulation_steps': None,
 'momentum': 0.0,
 'nesterov': False}

Die Standardeinstellung für die Lernrate ist also 0.01. Wir erstellen ein neues Objekt mit unserer gewünschten Lernrate:

opt = SGD(learning_rate = 0.1)
opt.get_config()

{'name': 'SGD',
 'learning_rate': 0.10000000149011612,
 'weight_decay': None,
 'clipnorm': None,
 'global_clipnorm': None,
 'clipvalue': None,
 'use_ema': False,
 'ema_momentum': 0.99,
 'ema_overwrite_frequency': None,
 'loss_scale_factor': None,
 'gradient_accumulation_steps': None,
 'momentum': 0.0,
 'nesterov': False}

5.5.5 Compile

Mit compile konfigurieren wir das Training zunächst nur und übergeben zum Beispiel die Optimiermethode als Objekt. Alternativ kann man als Parameter für optimizer den String sgd übergeben, dann werden für Lernrate etc. die Standardeinstellungen gewählt. Als Metrik für unsere Messungen wählen wir Accuracy, kurz acc.

model.compile(optimizer=opt,
              loss='categorical_crossentropy',
              metrics=['acc'])

5.5.6 Fit

Das eigentliche Training wird mit fit durchgeführt. Wichtig ist, dass fit den Verlauf der Metriken pro Epoche in einem History-Objekt zurückgibt. Will man die Fehler- und Performance-Entwicklung später visualisieren, muss man dieses Objekt speichern.

Die Methode hat außer den Daten und Epochen noch ein paar Parameter:

• mit batch_size können Sie die Größe der Minibatches angeben (Standardmäßig 32)
• mit validation_data übergibt man Daten, auf denen nach jeder Epoche das Modell evaluiert wird; wir benutzen hier die echten Testdaten und keine speziellen Validierungsdaten
• mit verbose kann man die Ausgabe steuern (z.B. mit verbose=0 ausschalten).

Um Batchtraining zu realisieren, wählen wir eine Batchgröße von 60000, und bilden damit das originale Backpropagation nach, wo in einer Epoche alle Trainingsbeispiele verarbeitet werden, bevor ein Update der Gewichte durchgeführt wird (siehe auch Abschnitt 3.6).

Wir unterdrücken die Ausgabe (verbose=0), messen aber die Trainingsdauer mit Hilfe der Funktion time aus dem gleichnamigen Paket (gibt die Sekunden seit 1.1.1970 0:00 Uhr zurück).

start_time = time.time() # Wir merken uns die Startzeit

history1 = model.fit(x_train, y_train_1hot, 
                     epochs=20,
                     batch_size=60000,
                     verbose=1,
                     validation_data = (x_test, y_test_1hot))

duration = time.time() - start_time # Wir berechnen die Dauer in Sek.
print(f'TRAININGSDAUER: {duration:.2f} Sek.')

Epoch 1/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 488ms/step - acc: 0.0878 - loss: 2.3608

1/1 ━━━━━━━━━━━━━━━━━━━━ 1s 635ms/step - acc: 0.0878 - loss: 2.3608 - val_acc: 0.1003 - val_loss: 2.3329

Epoch 2/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 281ms/step - acc: 0.0974 - loss: 2.3354

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 330ms/step - acc: 0.0974 - loss: 2.3354 - val_acc: 0.1104 - val_loss: 2.3127

Epoch 3/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 242ms/step - acc: 0.1099 - loss: 2.3150

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 281ms/step - acc: 0.1099 - loss: 2.3150 - val_acc: 0.1356 - val_loss: 2.2956

Epoch 4/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 158ms/step - acc: 0.1323 - loss: 2.2979

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 194ms/step - acc: 0.1323 - loss: 2.2979 - val_acc: 0.1705 - val_loss: 2.2806

Epoch 5/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 139ms/step - acc: 0.1662 - loss: 2.2830

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 177ms/step - acc: 0.1662 - loss: 2.2830 - val_acc: 0.2024 - val_loss: 2.2671

Epoch 6/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 132ms/step - acc: 0.2000 - loss: 2.2695

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 168ms/step - acc: 0.2000 - loss: 2.2695 - val_acc: 0.2308 - val_loss: 2.2545

Epoch 7/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 398ms/step - acc: 0.2287 - loss: 2.2569

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 442ms/step - acc: 0.2287 - loss: 2.2569 - val_acc: 0.2559 - val_loss: 2.2426

Epoch 8/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 218ms/step - acc: 0.2529 - loss: 2.2451

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 270ms/step - acc: 0.2529 - loss: 2.2451 - val_acc: 0.2773 - val_loss: 2.2311

Epoch 9/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 149ms/step - acc: 0.2751 - loss: 2.2338

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 188ms/step - acc: 0.2751 - loss: 2.2338 - val_acc: 0.2977 - val_loss: 2.2200

Epoch 10/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 256ms/step - acc: 0.2952 - loss: 2.2228

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 293ms/step - acc: 0.2952 - loss: 2.2228 - val_acc: 0.3170 - val_loss: 2.2091

Epoch 11/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 160ms/step - acc: 0.3145 - loss: 2.2120

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 203ms/step - acc: 0.3145 - loss: 2.2120 - val_acc: 0.3346 - val_loss: 2.1983

Epoch 12/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 123ms/step - acc: 0.3320 - loss: 2.2014

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 163ms/step - acc: 0.3320 - loss: 2.2014 - val_acc: 0.3553 - val_loss: 2.1877

Epoch 13/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 157ms/step - acc: 0.3509 - loss: 2.1909

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 193ms/step - acc: 0.3509 - loss: 2.1909 - val_acc: 0.3737 - val_loss: 2.1771

Epoch 14/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 126ms/step - acc: 0.3687 - loss: 2.1806

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 164ms/step - acc: 0.3687 - loss: 2.1806 - val_acc: 0.3900 - val_loss: 2.1667

Epoch 15/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 190ms/step - acc: 0.3857 - loss: 2.1703

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 230ms/step - acc: 0.3857 - loss: 2.1703 - val_acc: 0.4073 - val_loss: 2.1563

Epoch 16/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 156ms/step - acc: 0.4027 - loss: 2.1601

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 197ms/step - acc: 0.4027 - loss: 2.1601 - val_acc: 0.4253 - val_loss: 2.1460

Epoch 17/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 121ms/step - acc: 0.4178 - loss: 2.1500

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 157ms/step - acc: 0.4178 - loss: 2.1500 - val_acc: 0.4406 - val_loss: 2.1357

Epoch 18/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 151ms/step - acc: 0.4326 - loss: 2.1399

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 188ms/step - acc: 0.4326 - loss: 2.1399 - val_acc: 0.4521 - val_loss: 2.1255

Epoch 19/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 174ms/step - acc: 0.4463 - loss: 2.1299

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 217ms/step - acc: 0.4463 - loss: 2.1299 - val_acc: 0.4646 - val_loss: 2.1154

Epoch 20/20

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 157ms/step - acc: 0.4598 - loss: 2.1200

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 197ms/step - acc: 0.4598 - loss: 2.1200 - val_acc: 0.4778 - val_loss: 2.1053

TRAININGSDAUER: 5.37 Sek.

Die Trainingsdauer im Batchtraining ist mit 3 Sekunden für 20 Epochen extrem kurz.

5.5.7 Evaluation

Wir sehen uns die Entwicklung von Zielfunktion (Loss) und Accuracy an.

Dazu definieren wir vorab eine Hilfsfunktion.

def set_subplot(ax, y_label, traindata, testdata, ylim):
    e_range = range(1, len(traindata) + 1)
    ax.plot(e_range, traindata, 'b', label='Training')
    ax.plot(e_range, testdata, 'g', label='Test')
    ax.set_xlabel('Epochen')
    ax.set_ylabel(y_label)
    ax.legend()
    ax.grid()
    ax.set_ylim(ylim)
    ax.set_title(y_label)

Achten Sie bei den Plots immer auf die Grenzen der y-Achse (im Code set_ylim). Diese werden immer so gewählt, dass man die Kurve möglichst gut sieht. Hier haben wir das Interval 0 bis 0.6 für die Accuracy. Weiter unten haben wir ein anderes Interval. Dies muss man beim Vergleich der Kurven natürlich beachten.

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(15,4))

set_subplot(ax[0], 'Loss', history1.history['loss'], 
            history1.history['val_loss'], [0, 3])
set_subplot(ax[1], 'Accuracy', history1.history['acc'], 
            history1.history['val_acc'], [0, 0.6])

plt.show()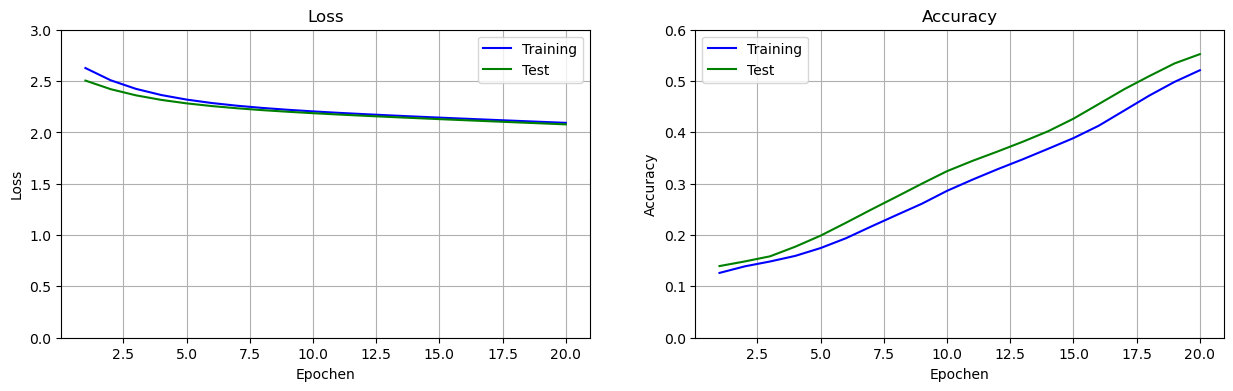

Mit evaluate können wir die Performanz unseres Modells auf den Testdaten messen. Wir bekommen ein Tupel mit Fehler und Accuracy zurück.

loss, acc = model.evaluate(x_test, y_test_1hot)
print(f"Evaluation auf den Testdaten:\n\nLoss = {loss:.3f}\nAccuracy = {acc:.3f}")

  1/313 ━━━━━━━━━━━━━━━━━━━━ 4s 16ms/step - acc: 0.6562 - loss: 2.0750

 80/313 ━━━━━━━━━━━━━━━━━━━━ 0s 637us/step - acc: 0.4362 - loss: 2.1287

158/313 ━━━━━━━━━━━━━━━━━━━━ 0s 640us/step - acc: 0.4327 - loss: 2.1291

256/313 ━━━━━━━━━━━━━━━━━━━━ 0s 592us/step - acc: 0.4412 - loss: 2.1246

313/313 ━━━━━━━━━━━━━━━━━━━━ 0s 615us/step - acc: 0.4474 - loss: 2.1213

Evaluation auf den Testdaten:

Loss = 2.105
Accuracy = 0.478

Mit Batchtraining erhalten wir nach 20 Epochen Training eine enttäuschende Accuracy von 47% auf den Testdaten.

5.6 Einfluss der Batchgröße

Mit Batchtraining (Batchgröße = 60000) haben wir ein enttäuschendes Ergebnis erzielt. Wir sehen uns jetzt das reine SGD und eine Variante von Minibatch-Training an. Beides wurde in Abschnitt 3.6 eingeführt.

5.6.1 Reines SGD (Batchgröße = 1)

Wenn wir die Batchgröße auf 1 setzen, erreichen wir “reines” Stochastic Gradient Descent, wo die Gewichte nach jedem Trainingsbeispiel angepasst werden.

Wir erzeugen eine neue Instanz des Netzwerks mit den gleichen Eigenschaften (20 versteckte Neuronen, gleiche Aktivierungsfunktionen). Anschließend trainieren wir es unter gleichen Bedingungen. Der einzige Unterschied ist die Batchgröße, die wir hier auf 1 setzen.

model = Sequential()
model.add(Input(shape=(784,)))
model.add(Dense(60, 
                activation='sigmoid'))
model.add(Dense(10, activation='softmax'))

opt = SGD(learning_rate = 0.1)

model.compile(optimizer=opt,
              loss='categorical_crossentropy',
              metrics=['acc'])

start_time = time.time() 

history2 = model.fit(x_train, y_train_1hot, 
                     epochs=20,
                     batch_size=1,
                     verbose=1,
                     validation_data = (x_test, y_test_1hot))

duration = time.time() - start_time 
print(f'TRAININGSDAUER: {duration:.2f} Sek.')

Epoch 1/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 2:32:21 152ms/step - acc: 0.0000e+00 - loss: 3.2959

   91/60000 ━━━━━━━━━━━━━━━━━━━━ 33s 556us/step - acc: 0.1307 - loss: 2.6126        

  194/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 518us/step - acc: 0.2005 - loss: 2.3502

  308/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 490us/step - acc: 0.2591 - loss: 2.1669

  408/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 493us/step - acc: 0.3020 - loss: 2.0336

  522/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 482us/step - acc: 0.3412 - loss: 1.9128

  636/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 474us/step - acc: 0.3749 - loss: 1.8123

  760/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 463us/step - acc: 0.4061 - loss: 1.7209

  872/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 461us/step - acc: 0.4301 - loss: 1.6497

  964/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 469us/step - acc: 0.4473 - loss: 1.5981

 1080/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 466us/step - acc: 0.4676 - loss: 1.5393

 1199/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 461us/step - acc: 0.4862 - loss: 1.4859

 1323/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 456us/step - acc: 0.5027 - loss: 1.4382

 1449/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 451us/step - acc: 0.5174 - loss: 1.3958

 1567/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 449us/step - acc: 0.5302 - loss: 1.3595

 1684/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 447us/step - acc: 0.5419 - loss: 1.3267

 1805/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 445us/step - acc: 0.5530 - loss: 1.2955

 1911/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 447us/step - acc: 0.5619 - loss: 1.2704

 2004/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 451us/step - acc: 0.5692 - loss: 1.2498

 2098/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 455us/step - acc: 0.5762 - loss: 1.2300

 2215/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 454us/step - acc: 0.5844 - loss: 1.2070

 2330/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 453us/step - acc: 0.5920 - loss: 1.1855

 2450/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 451us/step - acc: 0.5995 - loss: 1.1647

 2577/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 449us/step - acc: 0.6068 - loss: 1.1443

 2701/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 447us/step - acc: 0.6135 - loss: 1.1257

 2813/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 447us/step - acc: 0.6192 - loss: 1.1100

 2935/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 445us/step - acc: 0.6251 - loss: 1.0936

 3060/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 444us/step - acc: 0.6308 - loss: 1.0780

 3176/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 443us/step - acc: 0.6358 - loss: 1.0642

 3224/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 452us/step - acc: 0.6378 - loss: 1.0586

 3299/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 457us/step - acc: 0.6409 - loss: 1.0502

 3401/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 458us/step - acc: 0.6449 - loss: 1.0391

 3505/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 459us/step - acc: 0.6488 - loss: 1.0282

 3607/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 460us/step - acc: 0.6526 - loss: 1.0180

 3700/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 462us/step - acc: 0.6559 - loss: 1.0089

 3819/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 460us/step - acc: 0.6600 - loss: 0.9977

 3940/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 459us/step - acc: 0.6640 - loss: 0.9866

 4059/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 458us/step - acc: 0.6678 - loss: 0.9762

 4165/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 458us/step - acc: 0.6710 - loss: 0.9673

 4283/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 457us/step - acc: 0.6745 - loss: 0.9578

 4403/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 456us/step - acc: 0.6780 - loss: 0.9483

 4522/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 456us/step - acc: 0.6813 - loss: 0.9393

 4645/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 454us/step - acc: 0.6846 - loss: 0.9303

 4763/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 454us/step - acc: 0.6876 - loss: 0.9219

 4889/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 452us/step - acc: 0.6909 - loss: 0.9131

 5011/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 451us/step - acc: 0.6939 - loss: 0.9049

 5129/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 451us/step - acc: 0.6967 - loss: 0.8971

 5234/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 451us/step - acc: 0.6991 - loss: 0.8904

 5330/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 453us/step - acc: 0.7013 - loss: 0.8844

 5407/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 455us/step - acc: 0.7030 - loss: 0.8797

 5516/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 456us/step - acc: 0.7053 - loss: 0.8732

 5611/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 457us/step - acc: 0.7073 - loss: 0.8677

 5710/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 458us/step - acc: 0.7094 - loss: 0.8620

 5806/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 459us/step - acc: 0.7114 - loss: 0.8566

 5887/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 461us/step - acc: 0.7130 - loss: 0.8521

 5996/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 461us/step - acc: 0.7151 - loss: 0.8462

 6116/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 460us/step - acc: 0.7174 - loss: 0.8399

 6224/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 460us/step - acc: 0.7194 - loss: 0.8344

 6330/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 461us/step - acc: 0.7213 - loss: 0.8292

 6445/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 460us/step - acc: 0.7233 - loss: 0.8237

 6560/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 460us/step - acc: 0.7253 - loss: 0.8183

 6681/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 459us/step - acc: 0.7273 - loss: 0.8128

 6809/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 458us/step - acc: 0.7294 - loss: 0.8072

 6929/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 457us/step - acc: 0.7313 - loss: 0.8020

 7048/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 456us/step - acc: 0.7331 - loss: 0.7970

 7172/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 456us/step - acc: 0.7350 - loss: 0.7919

 7295/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 455us/step - acc: 0.7368 - loss: 0.7870

 7422/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 454us/step - acc: 0.7386 - loss: 0.7820

 7550/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 453us/step - acc: 0.7404 - loss: 0.7771

 7678/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 452us/step - acc: 0.7421 - loss: 0.7723

 7801/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 451us/step - acc: 0.7438 - loss: 0.7679

 7926/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 450us/step - acc: 0.7454 - loss: 0.7634

 8057/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 449us/step - acc: 0.7470 - loss: 0.7588

 8185/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 448us/step - acc: 0.7486 - loss: 0.7545

 8312/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 447us/step - acc: 0.7502 - loss: 0.7502

 8437/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 447us/step - acc: 0.7516 - loss: 0.7462

 8561/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 446us/step - acc: 0.7531 - loss: 0.7422

 8686/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 445us/step - acc: 0.7545 - loss: 0.7382

 8801/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 445us/step - acc: 0.7558 - loss: 0.7347

 8927/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 445us/step - acc: 0.7572 - loss: 0.7308

 9048/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 444us/step - acc: 0.7585 - loss: 0.7272

 9184/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 443us/step - acc: 0.7600 - loss: 0.7232

 9323/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 442us/step - acc: 0.7614 - loss: 0.7192

 9461/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 441us/step - acc: 0.7628 - loss: 0.7152

 9596/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 440us/step - acc: 0.7642 - loss: 0.7115

 9718/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 439us/step - acc: 0.7654 - loss: 0.7081

 9855/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 438us/step - acc: 0.7667 - loss: 0.7044

 9991/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 438us/step - acc: 0.7680 - loss: 0.7008

10117/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 437us/step - acc: 0.7692 - loss: 0.6976

10245/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 436us/step - acc: 0.7704 - loss: 0.6943

10379/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 436us/step - acc: 0.7716 - loss: 0.6910

10517/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 435us/step - acc: 0.7728 - loss: 0.6876

10654/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 434us/step - acc: 0.7740 - loss: 0.6843

10786/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 433us/step - acc: 0.7751 - loss: 0.6811

10910/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 433us/step - acc: 0.7761 - loss: 0.6782

11043/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 432us/step - acc: 0.7773 - loss: 0.6751

11166/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 432us/step - acc: 0.7783 - loss: 0.6724

11297/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 431us/step - acc: 0.7793 - loss: 0.6694

11433/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 431us/step - acc: 0.7804 - loss: 0.6664

11477/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 433us/step - acc: 0.7807 - loss: 0.6654

11612/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 433us/step - acc: 0.7818 - loss: 0.6625

11751/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 432us/step - acc: 0.7828 - loss: 0.6595

11884/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 431us/step - acc: 0.7838 - loss: 0.6567

12014/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 431us/step - acc: 0.7848 - loss: 0.6540

12148/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 430us/step - acc: 0.7858 - loss: 0.6512

12283/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 429us/step - acc: 0.7868 - loss: 0.6485

12414/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 429us/step - acc: 0.7877 - loss: 0.6459

12552/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 428us/step - acc: 0.7886 - loss: 0.6432

12679/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 428us/step - acc: 0.7895 - loss: 0.6407

12816/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 427us/step - acc: 0.7904 - loss: 0.6381

12952/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 427us/step - acc: 0.7913 - loss: 0.6356

13089/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 426us/step - acc: 0.7922 - loss: 0.6331

13224/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 425us/step - acc: 0.7931 - loss: 0.6306

13359/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 425us/step - acc: 0.7939 - loss: 0.6282

13493/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 424us/step - acc: 0.7948 - loss: 0.6259

13630/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 424us/step - acc: 0.7956 - loss: 0.6235

13769/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 423us/step - acc: 0.7965 - loss: 0.6211

13908/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 423us/step - acc: 0.7973 - loss: 0.6188

14044/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 422us/step - acc: 0.7981 - loss: 0.6166

14178/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 422us/step - acc: 0.7988 - loss: 0.6144

14316/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 421us/step - acc: 0.7996 - loss: 0.6122

14429/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 421us/step - acc: 0.8003 - loss: 0.6103

14517/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 422us/step - acc: 0.8008 - loss: 0.6090

14637/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 422us/step - acc: 0.8014 - loss: 0.6071

14757/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 422us/step - acc: 0.8021 - loss: 0.6052

14885/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 422us/step - acc: 0.8027 - loss: 0.6033

15018/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 421us/step - acc: 0.8034 - loss: 0.6013

15130/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 422us/step - acc: 0.8040 - loss: 0.5996

15248/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 422us/step - acc: 0.8046 - loss: 0.5979

15373/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 421us/step - acc: 0.8053 - loss: 0.5960

15509/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 421us/step - acc: 0.8060 - loss: 0.5941

15644/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 421us/step - acc: 0.8066 - loss: 0.5922

15779/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 420us/step - acc: 0.8073 - loss: 0.5903

15914/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 420us/step - acc: 0.8080 - loss: 0.5884

16054/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 419us/step - acc: 0.8086 - loss: 0.5865

16180/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 419us/step - acc: 0.8092 - loss: 0.5847

16317/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 419us/step - acc: 0.8099 - loss: 0.5829

16456/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 418us/step - acc: 0.8105 - loss: 0.5810

16584/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 418us/step - acc: 0.8111 - loss: 0.5794

16710/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 418us/step - acc: 0.8117 - loss: 0.5777

16846/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 417us/step - acc: 0.8123 - loss: 0.5759

16985/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 417us/step - acc: 0.8130 - loss: 0.5741

17122/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 416us/step - acc: 0.8136 - loss: 0.5724

17245/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 416us/step - acc: 0.8141 - loss: 0.5708

17364/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 416us/step - acc: 0.8146 - loss: 0.5693

17491/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 416us/step - acc: 0.8152 - loss: 0.5678

17619/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 416us/step - acc: 0.8157 - loss: 0.5662

17749/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 416us/step - acc: 0.8163 - loss: 0.5647

17870/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 416us/step - acc: 0.8168 - loss: 0.5632

17993/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 416us/step - acc: 0.8173 - loss: 0.5618

18122/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 416us/step - acc: 0.8178 - loss: 0.5603

18255/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 415us/step - acc: 0.8183 - loss: 0.5588

18386/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 415us/step - acc: 0.8188 - loss: 0.5573

18506/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 415us/step - acc: 0.8193 - loss: 0.5559

18639/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 415us/step - acc: 0.8198 - loss: 0.5544

18759/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 415us/step - acc: 0.8203 - loss: 0.5531

18884/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 415us/step - acc: 0.8208 - loss: 0.5517

19015/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 415us/step - acc: 0.8213 - loss: 0.5503

19148/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 414us/step - acc: 0.8218 - loss: 0.5489

19278/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 414us/step - acc: 0.8223 - loss: 0.5475

19410/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 414us/step - acc: 0.8227 - loss: 0.5461

19539/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 414us/step - acc: 0.8232 - loss: 0.5447

19674/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 413us/step - acc: 0.8237 - loss: 0.5433

19809/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 413us/step - acc: 0.8242 - loss: 0.5419

19947/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 413us/step - acc: 0.8247 - loss: 0.5405

20085/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 412us/step - acc: 0.8252 - loss: 0.5391

20223/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 412us/step - acc: 0.8256 - loss: 0.5377

20362/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 412us/step - acc: 0.8261 - loss: 0.5363

20489/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 412us/step - acc: 0.8266 - loss: 0.5350

20622/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 411us/step - acc: 0.8270 - loss: 0.5337

20752/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 411us/step - acc: 0.8275 - loss: 0.5325

20873/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 411us/step - acc: 0.8279 - loss: 0.5313

20999/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 411us/step - acc: 0.8283 - loss: 0.5301

21124/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 411us/step - acc: 0.8287 - loss: 0.5289

21257/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 411us/step - acc: 0.8291 - loss: 0.5277

21389/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 411us/step - acc: 0.8295 - loss: 0.5265

21511/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 411us/step - acc: 0.8299 - loss: 0.5254

21631/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 411us/step - acc: 0.8303 - loss: 0.5243

21761/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 411us/step - acc: 0.8307 - loss: 0.5231

21896/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 410us/step - acc: 0.8311 - loss: 0.5219

22034/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 410us/step - acc: 0.8316 - loss: 0.5206

22160/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 410us/step - acc: 0.8319 - loss: 0.5195

22292/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 410us/step - acc: 0.8323 - loss: 0.5184

22429/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 410us/step - acc: 0.8328 - loss: 0.5172

22567/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 409us/step - acc: 0.8332 - loss: 0.5160

22705/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 409us/step - acc: 0.8336 - loss: 0.5148

22838/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 409us/step - acc: 0.8340 - loss: 0.5137

22972/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 409us/step - acc: 0.8343 - loss: 0.5126

23109/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 408us/step - acc: 0.8347 - loss: 0.5114

23248/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 408us/step - acc: 0.8351 - loss: 0.5103

23386/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 408us/step - acc: 0.8355 - loss: 0.5092

23522/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 408us/step - acc: 0.8359 - loss: 0.5081

23658/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 407us/step - acc: 0.8363 - loss: 0.5070

23795/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 407us/step - acc: 0.8367 - loss: 0.5059

23914/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 407us/step - acc: 0.8370 - loss: 0.5050

24040/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 407us/step - acc: 0.8373 - loss: 0.5040

24163/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 407us/step - acc: 0.8377 - loss: 0.5031

24293/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 407us/step - acc: 0.8380 - loss: 0.5021

24419/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 407us/step - acc: 0.8383 - loss: 0.5011

24548/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 407us/step - acc: 0.8387 - loss: 0.5001

24677/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 407us/step - acc: 0.8390 - loss: 0.4992

24804/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 407us/step - acc: 0.8393 - loss: 0.4982

24929/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 407us/step - acc: 0.8396 - loss: 0.4973

25054/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 407us/step - acc: 0.8400 - loss: 0.4964

25183/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 407us/step - acc: 0.8403 - loss: 0.4955

25314/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 407us/step - acc: 0.8406 - loss: 0.4945

25442/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 407us/step - acc: 0.8409 - loss: 0.4936

25561/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 407us/step - acc: 0.8412 - loss: 0.4928

25690/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 407us/step - acc: 0.8415 - loss: 0.4919

25819/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 406us/step - acc: 0.8418 - loss: 0.4910

25953/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 406us/step - acc: 0.8422 - loss: 0.4900

26084/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 406us/step - acc: 0.8425 - loss: 0.4891

26154/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 407us/step - acc: 0.8426 - loss: 0.4887

26202/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 408us/step - acc: 0.8428 - loss: 0.4883

26219/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 410us/step - acc: 0.8428 - loss: 0.4882

26240/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 412us/step - acc: 0.8428 - loss: 0.4881

26259/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 413us/step - acc: 0.8429 - loss: 0.4879

26337/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 414us/step - acc: 0.8431 - loss: 0.4874

26438/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 414us/step - acc: 0.8433 - loss: 0.4867

26557/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 414us/step - acc: 0.8436 - loss: 0.4859

26688/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 414us/step - acc: 0.8439 - loss: 0.4851

26820/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 414us/step - acc: 0.8442 - loss: 0.4842

26950/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 414us/step - acc: 0.8445 - loss: 0.4833

27074/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 414us/step - acc: 0.8448 - loss: 0.4825

27202/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 414us/step - acc: 0.8451 - loss: 0.4817

27332/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 413us/step - acc: 0.8453 - loss: 0.4809

27463/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 413us/step - acc: 0.8456 - loss: 0.4800

27594/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 413us/step - acc: 0.8459 - loss: 0.4792

27710/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 413us/step - acc: 0.8462 - loss: 0.4785

27831/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 413us/step - acc: 0.8464 - loss: 0.4777

27966/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 413us/step - acc: 0.8467 - loss: 0.4769

28098/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 413us/step - acc: 0.8470 - loss: 0.4761

28230/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 413us/step - acc: 0.8473 - loss: 0.4752

28354/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 413us/step - acc: 0.8475 - loss: 0.4745

28484/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 413us/step - acc: 0.8478 - loss: 0.4737

28604/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 413us/step - acc: 0.8480 - loss: 0.4730

28734/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 412us/step - acc: 0.8483 - loss: 0.4722

28865/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 412us/step - acc: 0.8486 - loss: 0.4714

28998/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 412us/step - acc: 0.8489 - loss: 0.4706

29121/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 412us/step - acc: 0.8491 - loss: 0.4699

29255/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 412us/step - acc: 0.8494 - loss: 0.4691

29394/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 412us/step - acc: 0.8496 - loss: 0.4683

29517/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 412us/step - acc: 0.8499 - loss: 0.4676

29639/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 412us/step - acc: 0.8501 - loss: 0.4669

29753/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 412us/step - acc: 0.8504 - loss: 0.4663

29873/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 412us/step - acc: 0.8506 - loss: 0.4656

29990/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 412us/step - acc: 0.8508 - loss: 0.4649

30115/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 412us/step - acc: 0.8511 - loss: 0.4642

30234/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 412us/step - acc: 0.8513 - loss: 0.4636

30356/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 412us/step - acc: 0.8515 - loss: 0.4629

30485/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 412us/step - acc: 0.8518 - loss: 0.4622

30615/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 412us/step - acc: 0.8520 - loss: 0.4615

30745/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 412us/step - acc: 0.8522 - loss: 0.4607

30878/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 412us/step - acc: 0.8525 - loss: 0.4600

31010/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.8527 - loss: 0.4593

31135/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.8530 - loss: 0.4586

31253/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.8532 - loss: 0.4580

31378/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.8534 - loss: 0.4573

31505/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.8536 - loss: 0.4566

31638/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.8539 - loss: 0.4559

31766/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.8541 - loss: 0.4553

31894/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.8543 - loss: 0.4546

32024/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.8546 - loss: 0.4539

32142/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.8548 - loss: 0.4533

32265/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.8550 - loss: 0.4527

32393/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.8552 - loss: 0.4520

32519/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.8554 - loss: 0.4514

32642/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.8556 - loss: 0.4508

32772/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.8559 - loss: 0.4501

32886/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.8560 - loss: 0.4496

33014/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.8563 - loss: 0.4489

33139/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.8565 - loss: 0.4483

33267/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 411us/step - acc: 0.8567 - loss: 0.4477

33394/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 411us/step - acc: 0.8569 - loss: 0.4470

33518/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 411us/step - acc: 0.8571 - loss: 0.4464

33644/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 411us/step - acc: 0.8573 - loss: 0.4458

33771/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 410us/step - acc: 0.8575 - loss: 0.4452

33899/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 410us/step - acc: 0.8577 - loss: 0.4446

34027/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 410us/step - acc: 0.8579 - loss: 0.4440

34160/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 410us/step - acc: 0.8581 - loss: 0.4434

34295/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 410us/step - acc: 0.8584 - loss: 0.4427

34432/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 410us/step - acc: 0.8586 - loss: 0.4421

34566/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 410us/step - acc: 0.8588 - loss: 0.4415

34702/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 410us/step - acc: 0.8590 - loss: 0.4408

34839/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 409us/step - acc: 0.8592 - loss: 0.4402

34976/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 409us/step - acc: 0.8594 - loss: 0.4396

35112/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 409us/step - acc: 0.8596 - loss: 0.4389

35249/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 409us/step - acc: 0.8598 - loss: 0.4383

35370/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 409us/step - acc: 0.8600 - loss: 0.4378

35503/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 409us/step - acc: 0.8602 - loss: 0.4372

35630/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 409us/step - acc: 0.8604 - loss: 0.4366 

35761/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 409us/step - acc: 0.8606 - loss: 0.4360

35891/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 409us/step - acc: 0.8608 - loss: 0.4355

36018/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 409us/step - acc: 0.8610 - loss: 0.4349

36142/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 409us/step - acc: 0.8612 - loss: 0.4344

36273/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 408us/step - acc: 0.8614 - loss: 0.4338

36399/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 408us/step - acc: 0.8616 - loss: 0.4332

36532/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 408us/step - acc: 0.8618 - loss: 0.4327

36663/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 408us/step - acc: 0.8620 - loss: 0.4321

36800/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 408us/step - acc: 0.8622 - loss: 0.4315

36939/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 408us/step - acc: 0.8624 - loss: 0.4309

37076/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 408us/step - acc: 0.8625 - loss: 0.4303

37201/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 408us/step - acc: 0.8627 - loss: 0.4298

37336/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 408us/step - acc: 0.8629 - loss: 0.4292

37466/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 407us/step - acc: 0.8631 - loss: 0.4287

37589/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 407us/step - acc: 0.8633 - loss: 0.4282

37718/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 407us/step - acc: 0.8635 - loss: 0.4276

37850/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 407us/step - acc: 0.8636 - loss: 0.4271

37974/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 407us/step - acc: 0.8638 - loss: 0.4266

38096/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 407us/step - acc: 0.8640 - loss: 0.4261

38231/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 407us/step - acc: 0.8642 - loss: 0.4255

38366/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 407us/step - acc: 0.8644 - loss: 0.4250

38501/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 407us/step - acc: 0.8645 - loss: 0.4244

38636/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 407us/step - acc: 0.8647 - loss: 0.4239

38774/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 407us/step - acc: 0.8649 - loss: 0.4233

38900/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 407us/step - acc: 0.8651 - loss: 0.4228

39024/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 407us/step - acc: 0.8652 - loss: 0.4223

39156/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 407us/step - acc: 0.8654 - loss: 0.4218

39282/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 407us/step - acc: 0.8656 - loss: 0.4213

39414/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 406us/step - acc: 0.8658 - loss: 0.4208

39549/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 406us/step - acc: 0.8659 - loss: 0.4203

39673/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 406us/step - acc: 0.8661 - loss: 0.4198

39799/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 406us/step - acc: 0.8663 - loss: 0.4193

39934/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 406us/step - acc: 0.8664 - loss: 0.4188

40070/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 406us/step - acc: 0.8666 - loss: 0.4183

40207/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 406us/step - acc: 0.8668 - loss: 0.4177

40341/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 406us/step - acc: 0.8670 - loss: 0.4172

40473/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 406us/step - acc: 0.8671 - loss: 0.4167

40609/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 406us/step - acc: 0.8673 - loss: 0.4162

40742/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 406us/step - acc: 0.8675 - loss: 0.4157

40874/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.8676 - loss: 0.4152

41006/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.8678 - loss: 0.4147

41137/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.8680 - loss: 0.4143

41267/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.8681 - loss: 0.4138

41402/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.8683 - loss: 0.4133

41533/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.8684 - loss: 0.4128

41668/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.8686 - loss: 0.4123

41798/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.8688 - loss: 0.4118

41935/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.8689 - loss: 0.4114

42073/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.8691 - loss: 0.4109

42213/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 404us/step - acc: 0.8693 - loss: 0.4104

42350/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 404us/step - acc: 0.8694 - loss: 0.4099

42484/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 404us/step - acc: 0.8696 - loss: 0.4094

42619/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 404us/step - acc: 0.8697 - loss: 0.4089

42757/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 404us/step - acc: 0.8699 - loss: 0.4084

42886/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 404us/step - acc: 0.8701 - loss: 0.4080

43011/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 404us/step - acc: 0.8702 - loss: 0.4076

43132/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 404us/step - acc: 0.8703 - loss: 0.4071

43257/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 404us/step - acc: 0.8705 - loss: 0.4067

43379/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 404us/step - acc: 0.8706 - loss: 0.4063

43506/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 404us/step - acc: 0.8708 - loss: 0.4059

43643/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 404us/step - acc: 0.8709 - loss: 0.4054

43727/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 404us/step - acc: 0.8710 - loss: 0.4051

43774/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.8711 - loss: 0.4050

43891/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.8712 - loss: 0.4046

44010/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.8714 - loss: 0.4042

44140/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.8715 - loss: 0.4037

44267/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.8716 - loss: 0.4033

44393/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.8718 - loss: 0.4029

44522/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.8719 - loss: 0.4025

44646/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.8721 - loss: 0.4021

44777/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.8722 - loss: 0.4016

44903/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.8723 - loss: 0.4012

45032/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.8725 - loss: 0.4008

45161/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.8726 - loss: 0.4004

45288/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 405us/step - acc: 0.8728 - loss: 0.4000

45421/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 405us/step - acc: 0.8729 - loss: 0.3995

45550/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 405us/step - acc: 0.8730 - loss: 0.3991

45672/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 405us/step - acc: 0.8732 - loss: 0.3987

45804/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 405us/step - acc: 0.8733 - loss: 0.3983

45936/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.8735 - loss: 0.3979

46071/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.8736 - loss: 0.3975

46208/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.8737 - loss: 0.3971

46343/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.8739 - loss: 0.3966

46478/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.8740 - loss: 0.3962

46608/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.8742 - loss: 0.3958

46745/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.8743 - loss: 0.3954

46884/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.8744 - loss: 0.3950

47018/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.8746 - loss: 0.3946

47147/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.8747 - loss: 0.3942

47271/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.8748 - loss: 0.3938

47393/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.8750 - loss: 0.3935

47518/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.8751 - loss: 0.3931

47641/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8752 - loss: 0.3927

47767/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8753 - loss: 0.3923

47886/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8755 - loss: 0.3920

48009/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8756 - loss: 0.3916

48122/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8757 - loss: 0.3913

48231/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8758 - loss: 0.3910

48354/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8759 - loss: 0.3906

48478/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8760 - loss: 0.3902

48604/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8762 - loss: 0.3899

48721/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8763 - loss: 0.3895

48845/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8764 - loss: 0.3892

48971/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8765 - loss: 0.3888

49098/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8766 - loss: 0.3884

49225/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8768 - loss: 0.3881

49353/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8769 - loss: 0.3877

49478/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8770 - loss: 0.3874

49605/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8771 - loss: 0.3870

49735/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8772 - loss: 0.3866

49853/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8774 - loss: 0.3863

49976/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 404us/step - acc: 0.8775 - loss: 0.3860

50106/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8776 - loss: 0.3856

50237/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8777 - loss: 0.3852

50367/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8778 - loss: 0.3849

50493/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8780 - loss: 0.3845

50620/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8781 - loss: 0.3842

50744/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8782 - loss: 0.3839

50870/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8783 - loss: 0.3835

50992/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8784 - loss: 0.3832

51122/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8785 - loss: 0.3828

51250/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8787 - loss: 0.3825

51378/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8788 - loss: 0.3821

51507/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8789 - loss: 0.3818

51632/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8790 - loss: 0.3815

51757/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8791 - loss: 0.3811

51872/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8792 - loss: 0.3808

51992/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8793 - loss: 0.3805

52115/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8794 - loss: 0.3802

52242/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8795 - loss: 0.3798

52372/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8797 - loss: 0.3795

52496/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.8798 - loss: 0.3792

52620/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 404us/step - acc: 0.8799 - loss: 0.3789

52746/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 404us/step - acc: 0.8800 - loss: 0.3785

52873/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 404us/step - acc: 0.8801 - loss: 0.3782

53000/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 404us/step - acc: 0.8802 - loss: 0.3779

53127/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 404us/step - acc: 0.8803 - loss: 0.3776

53254/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 404us/step - acc: 0.8804 - loss: 0.3772

53382/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 404us/step - acc: 0.8805 - loss: 0.3769

53507/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 404us/step - acc: 0.8806 - loss: 0.3766

53637/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 404us/step - acc: 0.8807 - loss: 0.3763

53763/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 404us/step - acc: 0.8809 - loss: 0.3759

53893/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 403us/step - acc: 0.8810 - loss: 0.3756

54020/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 403us/step - acc: 0.8811 - loss: 0.3753

54146/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 403us/step - acc: 0.8812 - loss: 0.3750

54273/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 403us/step - acc: 0.8813 - loss: 0.3747

54396/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 403us/step - acc: 0.8814 - loss: 0.3744

54521/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 403us/step - acc: 0.8815 - loss: 0.3741

54648/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 403us/step - acc: 0.8816 - loss: 0.3737

54775/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 403us/step - acc: 0.8817 - loss: 0.3734

54902/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 403us/step - acc: 0.8818 - loss: 0.3731

55033/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 403us/step - acc: 0.8819 - loss: 0.3728

55158/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 403us/step - acc: 0.8820 - loss: 0.3725

55290/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 403us/step - acc: 0.8821 - loss: 0.3722

55407/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 403us/step - acc: 0.8822 - loss: 0.3719

55540/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 403us/step - acc: 0.8823 - loss: 0.3716

55663/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 403us/step - acc: 0.8824 - loss: 0.3713

55798/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 403us/step - acc: 0.8825 - loss: 0.3710

55916/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 403us/step - acc: 0.8826 - loss: 0.3707

56045/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 403us/step - acc: 0.8827 - loss: 0.3704

56165/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 403us/step - acc: 0.8828 - loss: 0.3701

56293/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 403us/step - acc: 0.8829 - loss: 0.3698

56410/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 403us/step - acc: 0.8830 - loss: 0.3695

56535/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 403us/step - acc: 0.8831 - loss: 0.3692

56653/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 403us/step - acc: 0.8832 - loss: 0.3689

56783/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 403us/step - acc: 0.8833 - loss: 0.3686

56902/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 403us/step - acc: 0.8834 - loss: 0.3684

57027/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 403us/step - acc: 0.8835 - loss: 0.3681

57149/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 403us/step - acc: 0.8836 - loss: 0.3678

57287/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 403us/step - acc: 0.8837 - loss: 0.3675

57415/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 403us/step - acc: 0.8838 - loss: 0.3672

57553/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 403us/step - acc: 0.8839 - loss: 0.3668

57676/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 403us/step - acc: 0.8840 - loss: 0.3666

57806/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 403us/step - acc: 0.8841 - loss: 0.3663

57929/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 403us/step - acc: 0.8842 - loss: 0.3660

58067/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 403us/step - acc: 0.8843 - loss: 0.3657

58195/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 403us/step - acc: 0.8844 - loss: 0.3654

58333/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 403us/step - acc: 0.8845 - loss: 0.3651

58460/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 403us/step - acc: 0.8846 - loss: 0.3648

58583/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 403us/step - acc: 0.8847 - loss: 0.3645

58708/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 403us/step - acc: 0.8848 - loss: 0.3642

58841/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 403us/step - acc: 0.8849 - loss: 0.3639

58965/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 403us/step - acc: 0.8850 - loss: 0.3636

59100/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 403us/step - acc: 0.8851 - loss: 0.3633

59226/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 403us/step - acc: 0.8852 - loss: 0.3631

59362/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 403us/step - acc: 0.8853 - loss: 0.3628

59489/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 403us/step - acc: 0.8854 - loss: 0.3625

59627/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 403us/step - acc: 0.8855 - loss: 0.3622

59755/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 403us/step - acc: 0.8856 - loss: 0.3619

59891/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 402us/step - acc: 0.8857 - loss: 0.3616

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 464us/step - acc: 0.8857 - loss: 0.3614 - val_acc: 0.9560 - val_loss: 0.1414

Epoch 2/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 10:30 11ms/step - acc: 1.0000 - loss: 2.0669e-04

  132/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 384us/step - acc: 0.9738 - loss: 0.1039     

  263/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 383us/step - acc: 0.9721 - loss: 0.1148

  397/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 380us/step - acc: 0.9692 - loss: 0.1208

  523/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 385us/step - acc: 0.9668 - loss: 0.1274

  656/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 383us/step - acc: 0.9657 - loss: 0.1297

  784/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 384us/step - acc: 0.9650 - loss: 0.1301

  912/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 386us/step - acc: 0.9650 - loss: 0.1295

 1048/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 384us/step - acc: 0.9651 - loss: 0.1286

 1185/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 382us/step - acc: 0.9645 - loss: 0.1295

 1323/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 380us/step - acc: 0.9642 - loss: 0.1297

 1460/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 378us/step - acc: 0.9642 - loss: 0.1296

 1597/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 377us/step - acc: 0.9641 - loss: 0.1294

 1732/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 377us/step - acc: 0.9642 - loss: 0.1287

 1868/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 376us/step - acc: 0.9644 - loss: 0.1279

 2006/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 375us/step - acc: 0.9646 - loss: 0.1269

 2142/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 375us/step - acc: 0.9648 - loss: 0.1258

 2276/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 375us/step - acc: 0.9649 - loss: 0.1250

 2413/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 374us/step - acc: 0.9651 - loss: 0.1241

 2550/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 374us/step - acc: 0.9652 - loss: 0.1233

 2686/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 374us/step - acc: 0.9654 - loss: 0.1225

 2823/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 373us/step - acc: 0.9655 - loss: 0.1219

 2961/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 373us/step - acc: 0.9656 - loss: 0.1214

 3101/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 372us/step - acc: 0.9656 - loss: 0.1209

 3237/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 372us/step - acc: 0.9657 - loss: 0.1205

 3378/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 372us/step - acc: 0.9657 - loss: 0.1201

 3515/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 371us/step - acc: 0.9657 - loss: 0.1197

 3642/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9657 - loss: 0.1194

 3768/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 373us/step - acc: 0.9657 - loss: 0.1190

 3897/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9657 - loss: 0.1188

 4025/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9657 - loss: 0.1185

 4157/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9657 - loss: 0.1183

 4290/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9657 - loss: 0.1181

 4418/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9657 - loss: 0.1180

 4549/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9656 - loss: 0.1180

 4687/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9656 - loss: 0.1180

 4823/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9655 - loss: 0.1180

 4959/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9655 - loss: 0.1180

 5095/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9655 - loss: 0.1179

 5233/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9655 - loss: 0.1179

 5364/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9654 - loss: 0.1179

 5497/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9654 - loss: 0.1178

 5635/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9654 - loss: 0.1178

 5770/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9654 - loss: 0.1178

 5905/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9653 - loss: 0.1179

 6040/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9653 - loss: 0.1179

 6173/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9653 - loss: 0.1179

 6306/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9653 - loss: 0.1180

 6446/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9653 - loss: 0.1180

 6584/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 373us/step - acc: 0.9652 - loss: 0.1181

 6723/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 373us/step - acc: 0.9652 - loss: 0.1182

 6850/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9652 - loss: 0.1182

 6968/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9652 - loss: 0.1183

 7103/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9651 - loss: 0.1183

 7240/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9651 - loss: 0.1184

 7377/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9651 - loss: 0.1184

 7514/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9651 - loss: 0.1185

 7653/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9651 - loss: 0.1185

 7790/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9650 - loss: 0.1185

 7929/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 373us/step - acc: 0.9650 - loss: 0.1185

 8070/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 373us/step - acc: 0.9650 - loss: 0.1185

 8210/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 373us/step - acc: 0.9650 - loss: 0.1186

 8333/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 373us/step - acc: 0.9650 - loss: 0.1186

 8470/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 373us/step - acc: 0.9650 - loss: 0.1186

 8608/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 373us/step - acc: 0.9649 - loss: 0.1186

 8745/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 373us/step - acc: 0.9649 - loss: 0.1186

 8879/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 373us/step - acc: 0.9649 - loss: 0.1187

 9015/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 373us/step - acc: 0.9649 - loss: 0.1187

 9152/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 373us/step - acc: 0.9649 - loss: 0.1187

 9290/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 373us/step - acc: 0.9649 - loss: 0.1187

 9425/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 373us/step - acc: 0.9648 - loss: 0.1188

 9559/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 373us/step - acc: 0.9648 - loss: 0.1188

 9697/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 373us/step - acc: 0.9648 - loss: 0.1189

 9828/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 373us/step - acc: 0.9648 - loss: 0.1189

 9961/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 373us/step - acc: 0.9648 - loss: 0.1190

10089/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 373us/step - acc: 0.9647 - loss: 0.1190

10196/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 374us/step - acc: 0.9647 - loss: 0.1191

10317/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 375us/step - acc: 0.9647 - loss: 0.1191

10455/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 375us/step - acc: 0.9647 - loss: 0.1192

10592/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 374us/step - acc: 0.9646 - loss: 0.1193

10730/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 374us/step - acc: 0.9646 - loss: 0.1193

10866/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 374us/step - acc: 0.9646 - loss: 0.1194

11003/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 374us/step - acc: 0.9645 - loss: 0.1195

11139/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 374us/step - acc: 0.9645 - loss: 0.1196

11277/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 374us/step - acc: 0.9645 - loss: 0.1196

11416/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 374us/step - acc: 0.9644 - loss: 0.1197

11554/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 374us/step - acc: 0.9644 - loss: 0.1198

11682/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 374us/step - acc: 0.9644 - loss: 0.1198

11806/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 374us/step - acc: 0.9643 - loss: 0.1199

11934/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 374us/step - acc: 0.9643 - loss: 0.1200

12068/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 374us/step - acc: 0.9643 - loss: 0.1200

12201/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 374us/step - acc: 0.9643 - loss: 0.1201

12337/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 374us/step - acc: 0.9642 - loss: 0.1201

12471/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 374us/step - acc: 0.9642 - loss: 0.1202

12608/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 374us/step - acc: 0.9642 - loss: 0.1203

12746/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 374us/step - acc: 0.9641 - loss: 0.1203

12879/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 374us/step - acc: 0.9641 - loss: 0.1204

13006/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 374us/step - acc: 0.9641 - loss: 0.1204

13142/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 374us/step - acc: 0.9641 - loss: 0.1205

13278/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 374us/step - acc: 0.9641 - loss: 0.1205

13413/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 374us/step - acc: 0.9640 - loss: 0.1206

13552/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 374us/step - acc: 0.9640 - loss: 0.1206

13686/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 374us/step - acc: 0.9640 - loss: 0.1207

13824/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 374us/step - acc: 0.9640 - loss: 0.1207

13963/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 374us/step - acc: 0.9639 - loss: 0.1208

14100/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 374us/step - acc: 0.9639 - loss: 0.1208

14239/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 374us/step - acc: 0.9639 - loss: 0.1209

14376/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 374us/step - acc: 0.9639 - loss: 0.1209

14514/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 373us/step - acc: 0.9638 - loss: 0.1210

14653/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 373us/step - acc: 0.9638 - loss: 0.1210

14788/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 373us/step - acc: 0.9638 - loss: 0.1210

14928/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 373us/step - acc: 0.9638 - loss: 0.1211

15066/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 373us/step - acc: 0.9638 - loss: 0.1211

15204/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 373us/step - acc: 0.9638 - loss: 0.1211

15342/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 373us/step - acc: 0.9637 - loss: 0.1212

15476/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 373us/step - acc: 0.9637 - loss: 0.1212

15610/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 373us/step - acc: 0.9637 - loss: 0.1212

15738/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 373us/step - acc: 0.9637 - loss: 0.1213

15858/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 373us/step - acc: 0.9637 - loss: 0.1213

15979/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 374us/step - acc: 0.9637 - loss: 0.1213

16052/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 375us/step - acc: 0.9636 - loss: 0.1214

16125/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 377us/step - acc: 0.9636 - loss: 0.1214

16139/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 379us/step - acc: 0.9636 - loss: 0.1214

16149/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 382us/step - acc: 0.9636 - loss: 0.1214

16162/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 385us/step - acc: 0.9636 - loss: 0.1214

16178/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 388us/step - acc: 0.9636 - loss: 0.1214

16234/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 390us/step - acc: 0.9636 - loss: 0.1214

16308/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 391us/step - acc: 0.9636 - loss: 0.1214

16419/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 392us/step - acc: 0.9636 - loss: 0.1214

16526/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 392us/step - acc: 0.9636 - loss: 0.1214

16638/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 393us/step - acc: 0.9636 - loss: 0.1214

16742/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 393us/step - acc: 0.9636 - loss: 0.1215

16858/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 393us/step - acc: 0.9636 - loss: 0.1215

16970/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 394us/step - acc: 0.9636 - loss: 0.1215

17082/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 394us/step - acc: 0.9635 - loss: 0.1215

17193/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 395us/step - acc: 0.9635 - loss: 0.1215

17305/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 395us/step - acc: 0.9635 - loss: 0.1215

17433/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 395us/step - acc: 0.9635 - loss: 0.1215

17539/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 395us/step - acc: 0.9635 - loss: 0.1215

17648/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 396us/step - acc: 0.9635 - loss: 0.1215

17754/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 396us/step - acc: 0.9635 - loss: 0.1215

17866/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 397us/step - acc: 0.9635 - loss: 0.1215

17979/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 397us/step - acc: 0.9635 - loss: 0.1215

18075/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 398us/step - acc: 0.9635 - loss: 0.1215

18178/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 398us/step - acc: 0.9635 - loss: 0.1215

18280/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 399us/step - acc: 0.9635 - loss: 0.1216

18395/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 399us/step - acc: 0.9635 - loss: 0.1216

18514/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 399us/step - acc: 0.9634 - loss: 0.1216

18639/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 399us/step - acc: 0.9634 - loss: 0.1216

18763/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 399us/step - acc: 0.9634 - loss: 0.1216

18888/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 399us/step - acc: 0.9634 - loss: 0.1216

18914/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 401us/step - acc: 0.9634 - loss: 0.1216

18963/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 403us/step - acc: 0.9634 - loss: 0.1216

19057/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 403us/step - acc: 0.9634 - loss: 0.1216

19141/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 404us/step - acc: 0.9634 - loss: 0.1216

19237/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 405us/step - acc: 0.9634 - loss: 0.1217

19317/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 406us/step - acc: 0.9634 - loss: 0.1217

19407/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 407us/step - acc: 0.9634 - loss: 0.1217

19519/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 407us/step - acc: 0.9634 - loss: 0.1217

19613/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 407us/step - acc: 0.9634 - loss: 0.1217

19709/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 408us/step - acc: 0.9633 - loss: 0.1217

19818/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 408us/step - acc: 0.9633 - loss: 0.1217

19926/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 409us/step - acc: 0.9633 - loss: 0.1218

20038/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 409us/step - acc: 0.9633 - loss: 0.1218

20128/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 409us/step - acc: 0.9633 - loss: 0.1218

20238/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 410us/step - acc: 0.9633 - loss: 0.1218

20357/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 410us/step - acc: 0.9633 - loss: 0.1218

20476/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 410us/step - acc: 0.9633 - loss: 0.1219

20589/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 410us/step - acc: 0.9633 - loss: 0.1219

20705/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 410us/step - acc: 0.9632 - loss: 0.1219

20830/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 410us/step - acc: 0.9632 - loss: 0.1219

20957/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 410us/step - acc: 0.9632 - loss: 0.1219

21079/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 410us/step - acc: 0.9632 - loss: 0.1220

21200/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 410us/step - acc: 0.9632 - loss: 0.1220

21322/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 410us/step - acc: 0.9632 - loss: 0.1220

21438/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 410us/step - acc: 0.9632 - loss: 0.1220

21547/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 410us/step - acc: 0.9632 - loss: 0.1220

21616/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 411us/step - acc: 0.9632 - loss: 0.1220

21708/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 412us/step - acc: 0.9632 - loss: 0.1220

21775/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 413us/step - acc: 0.9632 - loss: 0.1220

21885/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 413us/step - acc: 0.9631 - loss: 0.1220

22003/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 413us/step - acc: 0.9631 - loss: 0.1220

22127/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 413us/step - acc: 0.9631 - loss: 0.1220

22251/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 413us/step - acc: 0.9631 - loss: 0.1220

22366/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 413us/step - acc: 0.9631 - loss: 0.1221

22486/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 413us/step - acc: 0.9631 - loss: 0.1221

22603/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 414us/step - acc: 0.9631 - loss: 0.1221

22718/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 414us/step - acc: 0.9631 - loss: 0.1221

22803/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 414us/step - acc: 0.9631 - loss: 0.1221

22856/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 416us/step - acc: 0.9631 - loss: 0.1221

22967/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 416us/step - acc: 0.9631 - loss: 0.1221

23080/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 416us/step - acc: 0.9631 - loss: 0.1221

23201/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 416us/step - acc: 0.9631 - loss: 0.1221

23322/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 416us/step - acc: 0.9631 - loss: 0.1221

23448/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 416us/step - acc: 0.9631 - loss: 0.1222

23566/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 416us/step - acc: 0.9630 - loss: 0.1222

23686/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 416us/step - acc: 0.9630 - loss: 0.1222

23807/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 416us/step - acc: 0.9630 - loss: 0.1222

23911/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 416us/step - acc: 0.9630 - loss: 0.1222

24016/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 416us/step - acc: 0.9630 - loss: 0.1222

24105/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 417us/step - acc: 0.9630 - loss: 0.1222

24207/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 417us/step - acc: 0.9630 - loss: 0.1222

24317/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 417us/step - acc: 0.9630 - loss: 0.1222

24441/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 417us/step - acc: 0.9630 - loss: 0.1222

24525/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 418us/step - acc: 0.9630 - loss: 0.1222

24619/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 418us/step - acc: 0.9630 - loss: 0.1223

24727/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 419us/step - acc: 0.9630 - loss: 0.1223

24842/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 419us/step - acc: 0.9630 - loss: 0.1223

24929/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 419us/step - acc: 0.9630 - loss: 0.1223

25021/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 420us/step - acc: 0.9630 - loss: 0.1223

25115/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 420us/step - acc: 0.9630 - loss: 0.1223

25240/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 420us/step - acc: 0.9629 - loss: 0.1223

25355/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 420us/step - acc: 0.9629 - loss: 0.1223

25469/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 420us/step - acc: 0.9629 - loss: 0.1223

25583/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 420us/step - acc: 0.9629 - loss: 0.1223

25697/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 420us/step - acc: 0.9629 - loss: 0.1223

25793/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 421us/step - acc: 0.9629 - loss: 0.1223

25884/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 421us/step - acc: 0.9629 - loss: 0.1224

25956/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 422us/step - acc: 0.9629 - loss: 0.1224

26029/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 423us/step - acc: 0.9629 - loss: 0.1224

26132/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 423us/step - acc: 0.9629 - loss: 0.1224

26245/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 423us/step - acc: 0.9629 - loss: 0.1224

26360/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 423us/step - acc: 0.9629 - loss: 0.1224

26471/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 423us/step - acc: 0.9629 - loss: 0.1224

26562/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 424us/step - acc: 0.9629 - loss: 0.1224

26645/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 424us/step - acc: 0.9628 - loss: 0.1225

26751/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 425us/step - acc: 0.9628 - loss: 0.1225

26868/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 425us/step - acc: 0.9628 - loss: 0.1225

26959/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 425us/step - acc: 0.9628 - loss: 0.1225

27080/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 425us/step - acc: 0.9628 - loss: 0.1225

27188/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 425us/step - acc: 0.9628 - loss: 0.1225

27276/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 426us/step - acc: 0.9628 - loss: 0.1225

27381/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 426us/step - acc: 0.9628 - loss: 0.1225

27497/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 426us/step - acc: 0.9628 - loss: 0.1226

27619/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 426us/step - acc: 0.9628 - loss: 0.1226

27737/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 426us/step - acc: 0.9628 - loss: 0.1226

27841/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 426us/step - acc: 0.9628 - loss: 0.1226

27949/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 426us/step - acc: 0.9628 - loss: 0.1226

28064/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 426us/step - acc: 0.9628 - loss: 0.1226

28187/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 426us/step - acc: 0.9628 - loss: 0.1226

28304/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 426us/step - acc: 0.9628 - loss: 0.1226

28423/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 426us/step - acc: 0.9628 - loss: 0.1226

28542/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 426us/step - acc: 0.9627 - loss: 0.1227

28659/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 426us/step - acc: 0.9627 - loss: 0.1227

28773/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 426us/step - acc: 0.9627 - loss: 0.1227

28888/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 426us/step - acc: 0.9627 - loss: 0.1227

29004/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 426us/step - acc: 0.9627 - loss: 0.1227

29123/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 426us/step - acc: 0.9627 - loss: 0.1227

29238/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 426us/step - acc: 0.9627 - loss: 0.1227

29341/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 426us/step - acc: 0.9627 - loss: 0.1227

29417/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 427us/step - acc: 0.9627 - loss: 0.1227

29521/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 427us/step - acc: 0.9627 - loss: 0.1228

29629/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 427us/step - acc: 0.9627 - loss: 0.1228

29744/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 427us/step - acc: 0.9627 - loss: 0.1228

29856/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 428us/step - acc: 0.9627 - loss: 0.1228

29962/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 428us/step - acc: 0.9627 - loss: 0.1228

30068/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 428us/step - acc: 0.9627 - loss: 0.1228

30189/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 428us/step - acc: 0.9627 - loss: 0.1228

30287/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 428us/step - acc: 0.9627 - loss: 0.1228

30377/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 428us/step - acc: 0.9627 - loss: 0.1228

30491/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 429us/step - acc: 0.9627 - loss: 0.1229

30602/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 429us/step - acc: 0.9626 - loss: 0.1229

30711/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 429us/step - acc: 0.9626 - loss: 0.1229

30817/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 429us/step - acc: 0.9626 - loss: 0.1229

30926/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 429us/step - acc: 0.9626 - loss: 0.1229

31031/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 429us/step - acc: 0.9626 - loss: 0.1229

31140/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 429us/step - acc: 0.9626 - loss: 0.1229

31248/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 429us/step - acc: 0.9626 - loss: 0.1229

31362/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 429us/step - acc: 0.9626 - loss: 0.1229

31478/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 429us/step - acc: 0.9626 - loss: 0.1230

31563/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 430us/step - acc: 0.9626 - loss: 0.1230

31678/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 430us/step - acc: 0.9626 - loss: 0.1230

31796/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 430us/step - acc: 0.9626 - loss: 0.1230

31916/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 430us/step - acc: 0.9626 - loss: 0.1230

32040/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 430us/step - acc: 0.9626 - loss: 0.1230

32145/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 430us/step - acc: 0.9626 - loss: 0.1230

32261/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 430us/step - acc: 0.9626 - loss: 0.1230

32372/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 430us/step - acc: 0.9626 - loss: 0.1231

32484/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 430us/step - acc: 0.9626 - loss: 0.1231

32596/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 430us/step - acc: 0.9626 - loss: 0.1231

32705/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 430us/step - acc: 0.9625 - loss: 0.1231

32821/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 430us/step - acc: 0.9625 - loss: 0.1231

32928/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 430us/step - acc: 0.9625 - loss: 0.1231

33048/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 430us/step - acc: 0.9625 - loss: 0.1231

33175/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 430us/step - acc: 0.9625 - loss: 0.1232

33241/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 431us/step - acc: 0.9625 - loss: 0.1232

33327/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 431us/step - acc: 0.9625 - loss: 0.1232

33418/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 432us/step - acc: 0.9625 - loss: 0.1232

33515/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 432us/step - acc: 0.9625 - loss: 0.1232

33622/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 432us/step - acc: 0.9625 - loss: 0.1232

33682/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 433us/step - acc: 0.9625 - loss: 0.1232

33780/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 433us/step - acc: 0.9625 - loss: 0.1232

33898/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 433us/step - acc: 0.9625 - loss: 0.1233

33994/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 433us/step - acc: 0.9625 - loss: 0.1233

34098/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 433us/step - acc: 0.9625 - loss: 0.1233

34209/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 433us/step - acc: 0.9625 - loss: 0.1233

34330/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 433us/step - acc: 0.9625 - loss: 0.1233

34448/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 433us/step - acc: 0.9624 - loss: 0.1233

34570/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 433us/step - acc: 0.9624 - loss: 0.1233

34666/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 433us/step - acc: 0.9624 - loss: 0.1234

34786/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 433us/step - acc: 0.9624 - loss: 0.1234

34908/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 433us/step - acc: 0.9624 - loss: 0.1234

35030/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 433us/step - acc: 0.9624 - loss: 0.1234

35149/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 433us/step - acc: 0.9624 - loss: 0.1234

35266/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 433us/step - acc: 0.9624 - loss: 0.1234

35389/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 433us/step - acc: 0.9624 - loss: 0.1234

35478/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 433us/step - acc: 0.9624 - loss: 0.1234

35591/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 433us/step - acc: 0.9624 - loss: 0.1234

35707/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 433us/step - acc: 0.9624 - loss: 0.1235

35823/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 433us/step - acc: 0.9624 - loss: 0.1235

35923/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9624 - loss: 0.1235

36032/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9624 - loss: 0.1235

36146/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9624 - loss: 0.1235

36259/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9624 - loss: 0.1235

36368/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9624 - loss: 0.1235

36480/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9624 - loss: 0.1235

36596/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9624 - loss: 0.1235

36712/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9624 - loss: 0.1236

36832/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9623 - loss: 0.1236

36945/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9623 - loss: 0.1236

37062/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 434us/step - acc: 0.9623 - loss: 0.1236 

37181/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 434us/step - acc: 0.9623 - loss: 0.1236

37303/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 434us/step - acc: 0.9623 - loss: 0.1236

37424/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 434us/step - acc: 0.9623 - loss: 0.1236

37522/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 434us/step - acc: 0.9623 - loss: 0.1237

37622/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 434us/step - acc: 0.9623 - loss: 0.1237

37731/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 434us/step - acc: 0.9623 - loss: 0.1237

37845/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 434us/step - acc: 0.9623 - loss: 0.1237

37956/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 434us/step - acc: 0.9623 - loss: 0.1237

38067/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 434us/step - acc: 0.9623 - loss: 0.1237

38171/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 434us/step - acc: 0.9623 - loss: 0.1237

38275/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 435us/step - acc: 0.9623 - loss: 0.1238

38389/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 435us/step - acc: 0.9623 - loss: 0.1238

38503/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 435us/step - acc: 0.9623 - loss: 0.1238

38566/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 435us/step - acc: 0.9623 - loss: 0.1238

38670/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 435us/step - acc: 0.9623 - loss: 0.1238

38790/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 435us/step - acc: 0.9623 - loss: 0.1238

38911/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 435us/step - acc: 0.9623 - loss: 0.1238

39016/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 435us/step - acc: 0.9622 - loss: 0.1239

39124/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 435us/step - acc: 0.9622 - loss: 0.1239

39228/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 436us/step - acc: 0.9622 - loss: 0.1239

39339/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 436us/step - acc: 0.9622 - loss: 0.1239

39448/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 436us/step - acc: 0.9622 - loss: 0.1239

39556/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 436us/step - acc: 0.9622 - loss: 0.1239

39647/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 436us/step - acc: 0.9622 - loss: 0.1239

39758/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 436us/step - acc: 0.9622 - loss: 0.1240

39874/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 436us/step - acc: 0.9622 - loss: 0.1240

39995/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 436us/step - acc: 0.9622 - loss: 0.1240

40111/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 436us/step - acc: 0.9622 - loss: 0.1240

40226/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 436us/step - acc: 0.9622 - loss: 0.1240

40340/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 436us/step - acc: 0.9622 - loss: 0.1240

40463/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 436us/step - acc: 0.9622 - loss: 0.1240

40583/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 436us/step - acc: 0.9622 - loss: 0.1241

40691/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 436us/step - acc: 0.9622 - loss: 0.1241

40779/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 436us/step - acc: 0.9622 - loss: 0.1241

40844/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 437us/step - acc: 0.9622 - loss: 0.1241

40937/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 437us/step - acc: 0.9622 - loss: 0.1241

41039/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 437us/step - acc: 0.9622 - loss: 0.1241

41120/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 437us/step - acc: 0.9622 - loss: 0.1241

41227/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 438us/step - acc: 0.9621 - loss: 0.1241

41330/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 438us/step - acc: 0.9621 - loss: 0.1241

41433/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 438us/step - acc: 0.9621 - loss: 0.1242

41554/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 438us/step - acc: 0.9621 - loss: 0.1242

41671/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 438us/step - acc: 0.9621 - loss: 0.1242

41792/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 438us/step - acc: 0.9621 - loss: 0.1242

41908/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 438us/step - acc: 0.9621 - loss: 0.1242

41995/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 438us/step - acc: 0.9621 - loss: 0.1242

42103/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 438us/step - acc: 0.9621 - loss: 0.1242

42203/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 438us/step - acc: 0.9621 - loss: 0.1243

42295/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 438us/step - acc: 0.9621 - loss: 0.1243

42407/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 438us/step - acc: 0.9621 - loss: 0.1243

42508/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 439us/step - acc: 0.9621 - loss: 0.1243

42624/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 439us/step - acc: 0.9621 - loss: 0.1243

42735/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 439us/step - acc: 0.9621 - loss: 0.1243

42850/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 439us/step - acc: 0.9621 - loss: 0.1243

42970/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 439us/step - acc: 0.9621 - loss: 0.1244

43093/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 438us/step - acc: 0.9621 - loss: 0.1244

43214/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 438us/step - acc: 0.9621 - loss: 0.1244

43336/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 438us/step - acc: 0.9621 - loss: 0.1244

43425/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 439us/step - acc: 0.9621 - loss: 0.1244

43545/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 439us/step - acc: 0.9621 - loss: 0.1244

43664/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 438us/step - acc: 0.9620 - loss: 0.1244

43766/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 439us/step - acc: 0.9620 - loss: 0.1245

43899/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 438us/step - acc: 0.9620 - loss: 0.1245

44024/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 438us/step - acc: 0.9620 - loss: 0.1245

44142/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 438us/step - acc: 0.9620 - loss: 0.1245

44266/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 438us/step - acc: 0.9620 - loss: 0.1245

44392/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 438us/step - acc: 0.9620 - loss: 0.1245

44512/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 438us/step - acc: 0.9620 - loss: 0.1245

44632/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 438us/step - acc: 0.9620 - loss: 0.1246

44739/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 438us/step - acc: 0.9620 - loss: 0.1246

44844/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 438us/step - acc: 0.9620 - loss: 0.1246

44932/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 438us/step - acc: 0.9620 - loss: 0.1246

45051/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 438us/step - acc: 0.9620 - loss: 0.1246

45170/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 438us/step - acc: 0.9620 - loss: 0.1246

45266/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 438us/step - acc: 0.9620 - loss: 0.1246

45383/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 438us/step - acc: 0.9620 - loss: 0.1246

45501/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 438us/step - acc: 0.9620 - loss: 0.1246

45608/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 438us/step - acc: 0.9620 - loss: 0.1246

45712/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 439us/step - acc: 0.9620 - loss: 0.1247

45835/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 439us/step - acc: 0.9620 - loss: 0.1247

45951/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 439us/step - acc: 0.9620 - loss: 0.1247

46040/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 439us/step - acc: 0.9620 - loss: 0.1247

46152/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 439us/step - acc: 0.9620 - loss: 0.1247

46269/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 439us/step - acc: 0.9620 - loss: 0.1247

46394/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 439us/step - acc: 0.9620 - loss: 0.1247

46516/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 439us/step - acc: 0.9620 - loss: 0.1247

46641/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 438us/step - acc: 0.9620 - loss: 0.1247

46761/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 438us/step - acc: 0.9620 - loss: 0.1248

46875/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 438us/step - acc: 0.9619 - loss: 0.1248

46988/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 438us/step - acc: 0.9619 - loss: 0.1248

47114/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 438us/step - acc: 0.9619 - loss: 0.1248

47236/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 438us/step - acc: 0.9619 - loss: 0.1248

47357/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 438us/step - acc: 0.9619 - loss: 0.1248

47474/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 438us/step - acc: 0.9619 - loss: 0.1248

47589/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 438us/step - acc: 0.9619 - loss: 0.1248

47714/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 438us/step - acc: 0.9619 - loss: 0.1248

47843/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 438us/step - acc: 0.9619 - loss: 0.1249

47960/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 438us/step - acc: 0.9619 - loss: 0.1249

48074/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 438us/step - acc: 0.9619 - loss: 0.1249

48208/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 438us/step - acc: 0.9619 - loss: 0.1249

48343/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 438us/step - acc: 0.9619 - loss: 0.1249

48477/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 437us/step - acc: 0.9619 - loss: 0.1249

48613/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 437us/step - acc: 0.9619 - loss: 0.1249

48749/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 437us/step - acc: 0.9619 - loss: 0.1249

48883/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 437us/step - acc: 0.9619 - loss: 0.1249

49019/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 437us/step - acc: 0.9619 - loss: 0.1249

49155/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 436us/step - acc: 0.9619 - loss: 0.1250

49292/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 436us/step - acc: 0.9619 - loss: 0.1250

49400/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 436us/step - acc: 0.9619 - loss: 0.1250

49516/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 436us/step - acc: 0.9619 - loss: 0.1250

49638/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 436us/step - acc: 0.9619 - loss: 0.1250

49764/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 436us/step - acc: 0.9619 - loss: 0.1250

49884/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 436us/step - acc: 0.9619 - loss: 0.1250

50013/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 436us/step - acc: 0.9619 - loss: 0.1250

50137/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 436us/step - acc: 0.9619 - loss: 0.1250

50254/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 436us/step - acc: 0.9619 - loss: 0.1250

50376/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 436us/step - acc: 0.9619 - loss: 0.1250

50499/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 436us/step - acc: 0.9619 - loss: 0.1250

50578/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 436us/step - acc: 0.9619 - loss: 0.1250

50699/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 436us/step - acc: 0.9619 - loss: 0.1250

50815/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 436us/step - acc: 0.9619 - loss: 0.1251

50927/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 436us/step - acc: 0.9618 - loss: 0.1251

51030/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 436us/step - acc: 0.9618 - loss: 0.1251

51137/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 436us/step - acc: 0.9618 - loss: 0.1251

51247/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 436us/step - acc: 0.9618 - loss: 0.1251

51358/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 436us/step - acc: 0.9618 - loss: 0.1251

51459/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 436us/step - acc: 0.9618 - loss: 0.1251

51571/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 436us/step - acc: 0.9618 - loss: 0.1251

51695/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 436us/step - acc: 0.9618 - loss: 0.1251

51823/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 436us/step - acc: 0.9618 - loss: 0.1251

51941/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 436us/step - acc: 0.9618 - loss: 0.1251

52062/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 436us/step - acc: 0.9618 - loss: 0.1251

52173/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 436us/step - acc: 0.9618 - loss: 0.1251

52297/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 436us/step - acc: 0.9618 - loss: 0.1251

52400/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 436us/step - acc: 0.9618 - loss: 0.1251

52517/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 436us/step - acc: 0.9618 - loss: 0.1251

52639/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 436us/step - acc: 0.9618 - loss: 0.1252

52776/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 436us/step - acc: 0.9618 - loss: 0.1252

52906/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 436us/step - acc: 0.9618 - loss: 0.1252

53035/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 436us/step - acc: 0.9618 - loss: 0.1252

53164/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 436us/step - acc: 0.9618 - loss: 0.1252

53284/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 436us/step - acc: 0.9618 - loss: 0.1252

53415/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 436us/step - acc: 0.9618 - loss: 0.1252

53546/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 435us/step - acc: 0.9618 - loss: 0.1252

53680/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 435us/step - acc: 0.9618 - loss: 0.1252

53817/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 435us/step - acc: 0.9618 - loss: 0.1252

53954/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 435us/step - acc: 0.9618 - loss: 0.1252

54089/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 435us/step - acc: 0.9618 - loss: 0.1252

54224/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 435us/step - acc: 0.9618 - loss: 0.1252

54355/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 434us/step - acc: 0.9618 - loss: 0.1252

54487/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 434us/step - acc: 0.9618 - loss: 0.1252

54615/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 434us/step - acc: 0.9618 - loss: 0.1252

54752/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 434us/step - acc: 0.9618 - loss: 0.1252

54882/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 434us/step - acc: 0.9618 - loss: 0.1252

55015/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 434us/step - acc: 0.9618 - loss: 0.1252

55150/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 434us/step - acc: 0.9618 - loss: 0.1252

55286/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 433us/step - acc: 0.9618 - loss: 0.1253

55420/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 433us/step - acc: 0.9618 - loss: 0.1253

55554/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 433us/step - acc: 0.9618 - loss: 0.1253

55692/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 433us/step - acc: 0.9618 - loss: 0.1253

55830/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 433us/step - acc: 0.9618 - loss: 0.1253

55964/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 433us/step - acc: 0.9618 - loss: 0.1253

56101/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 433us/step - acc: 0.9618 - loss: 0.1253

56238/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 432us/step - acc: 0.9618 - loss: 0.1253

56378/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 432us/step - acc: 0.9618 - loss: 0.1253

56518/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 432us/step - acc: 0.9618 - loss: 0.1253

56653/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 432us/step - acc: 0.9618 - loss: 0.1253

56761/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 432us/step - acc: 0.9618 - loss: 0.1253

56788/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 433us/step - acc: 0.9618 - loss: 0.1253

56802/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 433us/step - acc: 0.9618 - loss: 0.1253

56812/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 434us/step - acc: 0.9618 - loss: 0.1253

56828/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 435us/step - acc: 0.9618 - loss: 0.1253

56888/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 435us/step - acc: 0.9618 - loss: 0.1253

56942/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 436us/step - acc: 0.9618 - loss: 0.1253

57068/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 436us/step - acc: 0.9618 - loss: 0.1253

57190/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 436us/step - acc: 0.9618 - loss: 0.1253

57315/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 436us/step - acc: 0.9618 - loss: 0.1253

57436/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 436us/step - acc: 0.9618 - loss: 0.1253

57562/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 436us/step - acc: 0.9618 - loss: 0.1253

57688/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 436us/step - acc: 0.9618 - loss: 0.1253

57820/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 435us/step - acc: 0.9618 - loss: 0.1253

57944/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 435us/step - acc: 0.9618 - loss: 0.1253

58068/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 435us/step - acc: 0.9618 - loss: 0.1253

58185/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 435us/step - acc: 0.9618 - loss: 0.1253

58303/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 435us/step - acc: 0.9618 - loss: 0.1253

58431/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 435us/step - acc: 0.9618 - loss: 0.1253

58553/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 435us/step - acc: 0.9618 - loss: 0.1253

58672/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 435us/step - acc: 0.9618 - loss: 0.1254

58781/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 435us/step - acc: 0.9617 - loss: 0.1254

58906/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 435us/step - acc: 0.9617 - loss: 0.1254

59025/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 435us/step - acc: 0.9617 - loss: 0.1254

59151/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 435us/step - acc: 0.9617 - loss: 0.1254

59274/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 435us/step - acc: 0.9617 - loss: 0.1254

59395/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 435us/step - acc: 0.9617 - loss: 0.1254

59511/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 435us/step - acc: 0.9617 - loss: 0.1254

59638/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 435us/step - acc: 0.9617 - loss: 0.1254

59744/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 435us/step - acc: 0.9617 - loss: 0.1254

59857/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 435us/step - acc: 0.9617 - loss: 0.1254

59972/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 435us/step - acc: 0.9617 - loss: 0.1254

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 497us/step - acc: 0.9617 - loss: 0.1254 - val_acc: 0.9556 - val_loss: 0.1414

Epoch 3/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 11:06 11ms/step - acc: 1.0000 - loss: 0.0898

  136/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 371us/step - acc: 0.9977 - loss: 0.0427 

  265/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 379us/step - acc: 0.9953 - loss: 0.0502

  400/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 377us/step - acc: 0.9939 - loss: 0.0504

  522/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 385us/step - acc: 0.9926 - loss: 0.0534

  638/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 393us/step - acc: 0.9918 - loss: 0.0546

  770/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 391us/step - acc: 0.9907 - loss: 0.0564

  901/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 390us/step - acc: 0.9901 - loss: 0.0570

 1031/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 389us/step - acc: 0.9895 - loss: 0.0574

 1155/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 391us/step - acc: 0.9889 - loss: 0.0576

 1288/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 389us/step - acc: 0.9885 - loss: 0.0576

 1423/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 388us/step - acc: 0.9878 - loss: 0.0585

 1552/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 388us/step - acc: 0.9873 - loss: 0.0596

 1681/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 388us/step - acc: 0.9867 - loss: 0.0604

 1815/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 387us/step - acc: 0.9863 - loss: 0.0611

 1942/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 387us/step - acc: 0.9859 - loss: 0.0618

 2072/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 387us/step - acc: 0.9855 - loss: 0.0623

 2198/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 388us/step - acc: 0.9851 - loss: 0.0629

 2322/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 389us/step - acc: 0.9848 - loss: 0.0634

 2453/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 388us/step - acc: 0.9844 - loss: 0.0640

 2587/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 388us/step - acc: 0.9840 - loss: 0.0647

 2723/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 387us/step - acc: 0.9835 - loss: 0.0653

 2860/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 386us/step - acc: 0.9831 - loss: 0.0660

 2996/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 385us/step - acc: 0.9827 - loss: 0.0668

 3134/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 384us/step - acc: 0.9823 - loss: 0.0676

 3270/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 383us/step - acc: 0.9819 - loss: 0.0683

 3396/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 384us/step - acc: 0.9815 - loss: 0.0690

 3526/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 384us/step - acc: 0.9812 - loss: 0.0697

 3658/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 384us/step - acc: 0.9808 - loss: 0.0704

 3789/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 384us/step - acc: 0.9805 - loss: 0.0712

 3923/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 384us/step - acc: 0.9801 - loss: 0.0720

 4055/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 383us/step - acc: 0.9798 - loss: 0.0728

 4189/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 383us/step - acc: 0.9795 - loss: 0.0736

 4328/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 382us/step - acc: 0.9792 - loss: 0.0743

 4452/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 383us/step - acc: 0.9789 - loss: 0.0750

 4588/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 383us/step - acc: 0.9787 - loss: 0.0757

 4725/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 382us/step - acc: 0.9784 - loss: 0.0763

 4859/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 382us/step - acc: 0.9782 - loss: 0.0768

 4996/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 382us/step - acc: 0.9780 - loss: 0.0774

 5132/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 381us/step - acc: 0.9778 - loss: 0.0780

 5267/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 381us/step - acc: 0.9775 - loss: 0.0785

 5404/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 381us/step - acc: 0.9773 - loss: 0.0790

 5542/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 380us/step - acc: 0.9771 - loss: 0.0795

 5681/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 380us/step - acc: 0.9770 - loss: 0.0799

 5811/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 380us/step - acc: 0.9768 - loss: 0.0803

 5941/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 380us/step - acc: 0.9766 - loss: 0.0807

 6075/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 380us/step - acc: 0.9765 - loss: 0.0810

 6211/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 380us/step - acc: 0.9763 - loss: 0.0814

 6348/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 379us/step - acc: 0.9762 - loss: 0.0817

 6484/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 379us/step - acc: 0.9761 - loss: 0.0820

 6621/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 379us/step - acc: 0.9760 - loss: 0.0823

 6756/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 379us/step - acc: 0.9759 - loss: 0.0825

 6893/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 379us/step - acc: 0.9758 - loss: 0.0828

 7029/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 378us/step - acc: 0.9757 - loss: 0.0830

 7165/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9756 - loss: 0.0832

 7302/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9755 - loss: 0.0835

 7441/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9754 - loss: 0.0837

 7571/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9753 - loss: 0.0839

 7701/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9752 - loss: 0.0841

 7829/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9751 - loss: 0.0843

 7959/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9751 - loss: 0.0845

 8092/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9750 - loss: 0.0847

 8229/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9749 - loss: 0.0850

 8363/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9748 - loss: 0.0852

 8496/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9747 - loss: 0.0854

 8626/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9747 - loss: 0.0856

 8760/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9746 - loss: 0.0858

 8899/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9745 - loss: 0.0861

 9037/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9744 - loss: 0.0863

 9176/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 377us/step - acc: 0.9743 - loss: 0.0865

 9313/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 377us/step - acc: 0.9743 - loss: 0.0866

 9451/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 377us/step - acc: 0.9742 - loss: 0.0868

 9591/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9741 - loss: 0.0870

 9730/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9741 - loss: 0.0872

 9860/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9740 - loss: 0.0873

 9992/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9740 - loss: 0.0875

10118/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9739 - loss: 0.0876

10242/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9739 - loss: 0.0877

10365/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 378us/step - acc: 0.9738 - loss: 0.0879

10487/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 378us/step - acc: 0.9738 - loss: 0.0880

10612/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 378us/step - acc: 0.9737 - loss: 0.0881

10736/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 379us/step - acc: 0.9737 - loss: 0.0882

10850/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 379us/step - acc: 0.9736 - loss: 0.0883

10967/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 380us/step - acc: 0.9736 - loss: 0.0884

11087/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 380us/step - acc: 0.9736 - loss: 0.0885

11209/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 381us/step - acc: 0.9735 - loss: 0.0886

11334/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 381us/step - acc: 0.9735 - loss: 0.0887

11459/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 381us/step - acc: 0.9734 - loss: 0.0888

11579/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 382us/step - acc: 0.9734 - loss: 0.0889

11699/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 382us/step - acc: 0.9734 - loss: 0.0890

11826/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 382us/step - acc: 0.9733 - loss: 0.0891

11950/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 382us/step - acc: 0.9733 - loss: 0.0892

12074/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 383us/step - acc: 0.9732 - loss: 0.0893

12195/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 383us/step - acc: 0.9732 - loss: 0.0894

12320/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 383us/step - acc: 0.9732 - loss: 0.0894

12443/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 383us/step - acc: 0.9731 - loss: 0.0895

12569/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 383us/step - acc: 0.9731 - loss: 0.0896

12690/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 384us/step - acc: 0.9731 - loss: 0.0897

12815/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 384us/step - acc: 0.9730 - loss: 0.0897

12937/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 384us/step - acc: 0.9730 - loss: 0.0898

13054/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 385us/step - acc: 0.9730 - loss: 0.0899

13172/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 385us/step - acc: 0.9729 - loss: 0.0899

13289/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 385us/step - acc: 0.9729 - loss: 0.0900

13406/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 386us/step - acc: 0.9729 - loss: 0.0901

13528/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 386us/step - acc: 0.9729 - loss: 0.0901

13649/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 386us/step - acc: 0.9728 - loss: 0.0902

13735/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 387us/step - acc: 0.9728 - loss: 0.0903

13845/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 388us/step - acc: 0.9728 - loss: 0.0903

13941/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 389us/step - acc: 0.9728 - loss: 0.0904

14051/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 389us/step - acc: 0.9727 - loss: 0.0904

14175/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 390us/step - acc: 0.9727 - loss: 0.0905

14297/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 390us/step - acc: 0.9727 - loss: 0.0906

14417/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 390us/step - acc: 0.9727 - loss: 0.0907

14535/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 390us/step - acc: 0.9726 - loss: 0.0907

14636/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 391us/step - acc: 0.9726 - loss: 0.0908

14749/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 391us/step - acc: 0.9726 - loss: 0.0909

14871/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 392us/step - acc: 0.9726 - loss: 0.0910

14993/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 392us/step - acc: 0.9725 - loss: 0.0910

15116/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 392us/step - acc: 0.9725 - loss: 0.0911

15234/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 392us/step - acc: 0.9725 - loss: 0.0912

15335/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 393us/step - acc: 0.9725 - loss: 0.0912

15444/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 393us/step - acc: 0.9725 - loss: 0.0913

15557/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 394us/step - acc: 0.9724 - loss: 0.0914

15671/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 394us/step - acc: 0.9724 - loss: 0.0914

15788/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 394us/step - acc: 0.9724 - loss: 0.0915

15904/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 395us/step - acc: 0.9724 - loss: 0.0916

16028/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 395us/step - acc: 0.9723 - loss: 0.0916

16152/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 395us/step - acc: 0.9723 - loss: 0.0917

16279/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 395us/step - acc: 0.9723 - loss: 0.0918

16394/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 395us/step - acc: 0.9723 - loss: 0.0918

16509/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 395us/step - acc: 0.9723 - loss: 0.0919

16637/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 395us/step - acc: 0.9723 - loss: 0.0919

16750/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 396us/step - acc: 0.9722 - loss: 0.0920

16878/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 396us/step - acc: 0.9722 - loss: 0.0920

17007/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 396us/step - acc: 0.9722 - loss: 0.0921

17120/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 396us/step - acc: 0.9722 - loss: 0.0921

17242/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 396us/step - acc: 0.9722 - loss: 0.0922

17365/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 396us/step - acc: 0.9722 - loss: 0.0922

17491/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 396us/step - acc: 0.9721 - loss: 0.0923

17606/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 396us/step - acc: 0.9721 - loss: 0.0923

17736/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 396us/step - acc: 0.9721 - loss: 0.0924

17857/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 396us/step - acc: 0.9721 - loss: 0.0924

17984/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 396us/step - acc: 0.9721 - loss: 0.0924

18115/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 396us/step - acc: 0.9721 - loss: 0.0925

18228/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 397us/step - acc: 0.9721 - loss: 0.0925

18349/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 397us/step - acc: 0.9720 - loss: 0.0926

18465/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 397us/step - acc: 0.9720 - loss: 0.0926

18578/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 397us/step - acc: 0.9720 - loss: 0.0927

18700/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 397us/step - acc: 0.9720 - loss: 0.0927

18823/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 397us/step - acc: 0.9720 - loss: 0.0927

18947/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 397us/step - acc: 0.9720 - loss: 0.0928

19073/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 398us/step - acc: 0.9720 - loss: 0.0928

19196/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 398us/step - acc: 0.9719 - loss: 0.0929

19322/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 398us/step - acc: 0.9719 - loss: 0.0929

19448/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 398us/step - acc: 0.9719 - loss: 0.0930

19578/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 398us/step - acc: 0.9719 - loss: 0.0930

19701/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 398us/step - acc: 0.9719 - loss: 0.0931

19831/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 398us/step - acc: 0.9719 - loss: 0.0931

19941/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 398us/step - acc: 0.9719 - loss: 0.0931

20058/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 398us/step - acc: 0.9719 - loss: 0.0932

20192/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 398us/step - acc: 0.9718 - loss: 0.0932

20326/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 398us/step - acc: 0.9718 - loss: 0.0933

20460/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 398us/step - acc: 0.9718 - loss: 0.0933

20597/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 397us/step - acc: 0.9718 - loss: 0.0933

20727/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 397us/step - acc: 0.9718 - loss: 0.0934

20863/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 397us/step - acc: 0.9718 - loss: 0.0934

20999/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 397us/step - acc: 0.9718 - loss: 0.0935

21136/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 397us/step - acc: 0.9718 - loss: 0.0935

21275/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 396us/step - acc: 0.9717 - loss: 0.0936

21408/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 396us/step - acc: 0.9717 - loss: 0.0936

21545/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 396us/step - acc: 0.9717 - loss: 0.0937

21680/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 396us/step - acc: 0.9717 - loss: 0.0937

21816/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 396us/step - acc: 0.9717 - loss: 0.0937

21953/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 396us/step - acc: 0.9717 - loss: 0.0938

22088/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 396us/step - acc: 0.9717 - loss: 0.0938

22219/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 395us/step - acc: 0.9716 - loss: 0.0939

22347/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 395us/step - acc: 0.9716 - loss: 0.0939

22479/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 395us/step - acc: 0.9716 - loss: 0.0940

22615/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 395us/step - acc: 0.9716 - loss: 0.0940

22745/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 395us/step - acc: 0.9716 - loss: 0.0940

22874/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 395us/step - acc: 0.9716 - loss: 0.0941

23001/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 395us/step - acc: 0.9716 - loss: 0.0941

23132/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 395us/step - acc: 0.9716 - loss: 0.0942

23267/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 395us/step - acc: 0.9715 - loss: 0.0942

23401/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 395us/step - acc: 0.9715 - loss: 0.0942

23535/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 395us/step - acc: 0.9715 - loss: 0.0943

23671/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 395us/step - acc: 0.9715 - loss: 0.0943

23809/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 394us/step - acc: 0.9715 - loss: 0.0944

23942/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 394us/step - acc: 0.9715 - loss: 0.0944

24074/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 394us/step - acc: 0.9715 - loss: 0.0944

24212/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 394us/step - acc: 0.9715 - loss: 0.0945

24349/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 394us/step - acc: 0.9714 - loss: 0.0945

24490/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 394us/step - acc: 0.9714 - loss: 0.0946

24627/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 393us/step - acc: 0.9714 - loss: 0.0946

24767/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 393us/step - acc: 0.9714 - loss: 0.0946

24903/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 393us/step - acc: 0.9714 - loss: 0.0947

25040/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 393us/step - acc: 0.9714 - loss: 0.0947

25180/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 393us/step - acc: 0.9714 - loss: 0.0947

25271/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 393us/step - acc: 0.9714 - loss: 0.0947

25366/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 394us/step - acc: 0.9714 - loss: 0.0948

25495/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 394us/step - acc: 0.9714 - loss: 0.0948

25623/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 394us/step - acc: 0.9714 - loss: 0.0948

25760/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 394us/step - acc: 0.9714 - loss: 0.0948

25898/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 394us/step - acc: 0.9713 - loss: 0.0948

26028/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 394us/step - acc: 0.9713 - loss: 0.0949

26157/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 393us/step - acc: 0.9713 - loss: 0.0949

26293/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 393us/step - acc: 0.9713 - loss: 0.0949

26430/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 393us/step - acc: 0.9713 - loss: 0.0949

26570/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 393us/step - acc: 0.9713 - loss: 0.0950

26702/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 393us/step - acc: 0.9713 - loss: 0.0950

26840/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 393us/step - acc: 0.9713 - loss: 0.0950

26971/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 393us/step - acc: 0.9713 - loss: 0.0950

27107/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 393us/step - acc: 0.9713 - loss: 0.0951

27241/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 393us/step - acc: 0.9713 - loss: 0.0951

27378/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 392us/step - acc: 0.9713 - loss: 0.0951

27517/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 392us/step - acc: 0.9713 - loss: 0.0951

27654/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 392us/step - acc: 0.9712 - loss: 0.0952

27792/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 392us/step - acc: 0.9712 - loss: 0.0952

27920/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 392us/step - acc: 0.9712 - loss: 0.0952

28051/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 392us/step - acc: 0.9712 - loss: 0.0952

28188/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 392us/step - acc: 0.9712 - loss: 0.0953

28324/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 392us/step - acc: 0.9712 - loss: 0.0953

28456/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 392us/step - acc: 0.9712 - loss: 0.0953

28576/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 392us/step - acc: 0.9712 - loss: 0.0953

28711/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 392us/step - acc: 0.9712 - loss: 0.0953

28841/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 392us/step - acc: 0.9712 - loss: 0.0954

28970/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 392us/step - acc: 0.9712 - loss: 0.0954

29105/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 392us/step - acc: 0.9712 - loss: 0.0954

29237/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 392us/step - acc: 0.9712 - loss: 0.0954

29374/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 391us/step - acc: 0.9712 - loss: 0.0955

29512/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 391us/step - acc: 0.9711 - loss: 0.0955

29650/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 391us/step - acc: 0.9711 - loss: 0.0955

29788/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 391us/step - acc: 0.9711 - loss: 0.0955

29922/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 391us/step - acc: 0.9711 - loss: 0.0956

30060/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 391us/step - acc: 0.9711 - loss: 0.0956

30198/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 391us/step - acc: 0.9711 - loss: 0.0956

30337/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 391us/step - acc: 0.9711 - loss: 0.0956

30475/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9711 - loss: 0.0956

30611/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9711 - loss: 0.0957

30750/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9711 - loss: 0.0957

30887/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9711 - loss: 0.0957

31025/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9711 - loss: 0.0957

31159/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9711 - loss: 0.0958

31295/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9711 - loss: 0.0958

31431/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9710 - loss: 0.0958

31565/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9710 - loss: 0.0958

31702/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9710 - loss: 0.0958

31834/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 390us/step - acc: 0.9710 - loss: 0.0959

31966/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 389us/step - acc: 0.9710 - loss: 0.0959

32098/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 389us/step - acc: 0.9710 - loss: 0.0959

32234/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 389us/step - acc: 0.9710 - loss: 0.0959

32371/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 389us/step - acc: 0.9710 - loss: 0.0960

32505/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 389us/step - acc: 0.9710 - loss: 0.0960

32633/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 389us/step - acc: 0.9710 - loss: 0.0960

32762/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 389us/step - acc: 0.9710 - loss: 0.0960

32897/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 389us/step - acc: 0.9710 - loss: 0.0960

33030/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 389us/step - acc: 0.9710 - loss: 0.0961

33167/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 389us/step - acc: 0.9710 - loss: 0.0961

33301/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 389us/step - acc: 0.9710 - loss: 0.0961

33436/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 389us/step - acc: 0.9709 - loss: 0.0961

33573/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 389us/step - acc: 0.9709 - loss: 0.0962

33709/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 389us/step - acc: 0.9709 - loss: 0.0962

33847/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 389us/step - acc: 0.9709 - loss: 0.0962

33984/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 389us/step - acc: 0.9709 - loss: 0.0962

34120/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 388us/step - acc: 0.9709 - loss: 0.0962

34257/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 388us/step - acc: 0.9709 - loss: 0.0963 

34395/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 388us/step - acc: 0.9709 - loss: 0.0963

34533/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 388us/step - acc: 0.9709 - loss: 0.0963

34672/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 388us/step - acc: 0.9709 - loss: 0.0963

34806/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 388us/step - acc: 0.9709 - loss: 0.0963

34943/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 388us/step - acc: 0.9709 - loss: 0.0964

35082/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 388us/step - acc: 0.9709 - loss: 0.0964

35220/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 388us/step - acc: 0.9709 - loss: 0.0964

35348/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 388us/step - acc: 0.9708 - loss: 0.0964

35472/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 388us/step - acc: 0.9708 - loss: 0.0964

35606/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 388us/step - acc: 0.9708 - loss: 0.0965

35742/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 388us/step - acc: 0.9708 - loss: 0.0965

35874/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 388us/step - acc: 0.9708 - loss: 0.0965

36004/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 388us/step - acc: 0.9708 - loss: 0.0965

36140/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 388us/step - acc: 0.9708 - loss: 0.0965

36270/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 388us/step - acc: 0.9708 - loss: 0.0966

36403/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 388us/step - acc: 0.9708 - loss: 0.0966

36529/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 388us/step - acc: 0.9708 - loss: 0.0966

36667/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 387us/step - acc: 0.9708 - loss: 0.0966

36803/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 387us/step - acc: 0.9708 - loss: 0.0966

36937/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 387us/step - acc: 0.9708 - loss: 0.0967

37071/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 387us/step - acc: 0.9708 - loss: 0.0967

37207/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 387us/step - acc: 0.9708 - loss: 0.0967

37342/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 387us/step - acc: 0.9707 - loss: 0.0967

37478/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 387us/step - acc: 0.9707 - loss: 0.0967

37607/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 387us/step - acc: 0.9707 - loss: 0.0968

37744/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 387us/step - acc: 0.9707 - loss: 0.0968

37879/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 387us/step - acc: 0.9707 - loss: 0.0968

38015/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 387us/step - acc: 0.9707 - loss: 0.0968

38151/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 387us/step - acc: 0.9707 - loss: 0.0968

38283/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 387us/step - acc: 0.9707 - loss: 0.0968

38419/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 387us/step - acc: 0.9707 - loss: 0.0969

38552/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 387us/step - acc: 0.9707 - loss: 0.0969

38685/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 387us/step - acc: 0.9707 - loss: 0.0969

38822/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 387us/step - acc: 0.9707 - loss: 0.0969

38958/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 387us/step - acc: 0.9707 - loss: 0.0969

39095/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 387us/step - acc: 0.9707 - loss: 0.0970

39231/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 386us/step - acc: 0.9707 - loss: 0.0970

39368/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 386us/step - acc: 0.9706 - loss: 0.0970

39504/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 386us/step - acc: 0.9706 - loss: 0.0970

39639/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 386us/step - acc: 0.9706 - loss: 0.0970

39776/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 386us/step - acc: 0.9706 - loss: 0.0970

39913/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 386us/step - acc: 0.9706 - loss: 0.0971

40046/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 386us/step - acc: 0.9706 - loss: 0.0971

40180/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 386us/step - acc: 0.9706 - loss: 0.0971

40314/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 386us/step - acc: 0.9706 - loss: 0.0971

40448/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 386us/step - acc: 0.9706 - loss: 0.0971

40584/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 386us/step - acc: 0.9706 - loss: 0.0971

40725/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 386us/step - acc: 0.9706 - loss: 0.0972

40860/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 386us/step - acc: 0.9706 - loss: 0.0972

40996/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 386us/step - acc: 0.9706 - loss: 0.0972

41131/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 386us/step - acc: 0.9706 - loss: 0.0972

41265/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 386us/step - acc: 0.9706 - loss: 0.0972

41395/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 386us/step - acc: 0.9705 - loss: 0.0973

41530/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 386us/step - acc: 0.9705 - loss: 0.0973

41664/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 386us/step - acc: 0.9705 - loss: 0.0973

41797/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 386us/step - acc: 0.9705 - loss: 0.0973

41928/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 386us/step - acc: 0.9705 - loss: 0.0973

42064/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 385us/step - acc: 0.9705 - loss: 0.0974

42201/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 385us/step - acc: 0.9705 - loss: 0.0974

42336/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 385us/step - acc: 0.9705 - loss: 0.0974

42472/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 385us/step - acc: 0.9705 - loss: 0.0974

42608/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 385us/step - acc: 0.9705 - loss: 0.0974

42743/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 385us/step - acc: 0.9705 - loss: 0.0975

42878/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 385us/step - acc: 0.9705 - loss: 0.0975

43012/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 385us/step - acc: 0.9705 - loss: 0.0975

43146/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 385us/step - acc: 0.9705 - loss: 0.0975

43283/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 385us/step - acc: 0.9704 - loss: 0.0975

43420/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 385us/step - acc: 0.9704 - loss: 0.0976

43557/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 385us/step - acc: 0.9704 - loss: 0.0976

43694/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 385us/step - acc: 0.9704 - loss: 0.0976

43832/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 385us/step - acc: 0.9704 - loss: 0.0976

43969/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 385us/step - acc: 0.9704 - loss: 0.0977

44095/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 385us/step - acc: 0.9704 - loss: 0.0977

44228/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 385us/step - acc: 0.9704 - loss: 0.0977

44365/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 385us/step - acc: 0.9704 - loss: 0.0977

44498/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 385us/step - acc: 0.9704 - loss: 0.0977

44632/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 385us/step - acc: 0.9704 - loss: 0.0978

44767/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 385us/step - acc: 0.9704 - loss: 0.0978

44897/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 385us/step - acc: 0.9704 - loss: 0.0978

45031/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 385us/step - acc: 0.9704 - loss: 0.0978

45166/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 385us/step - acc: 0.9703 - loss: 0.0978

45300/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 385us/step - acc: 0.9703 - loss: 0.0978

45433/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 385us/step - acc: 0.9703 - loss: 0.0979

45569/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 384us/step - acc: 0.9703 - loss: 0.0979

45703/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 384us/step - acc: 0.9703 - loss: 0.0979

45839/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 384us/step - acc: 0.9703 - loss: 0.0979

45973/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 384us/step - acc: 0.9703 - loss: 0.0979

46113/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 384us/step - acc: 0.9703 - loss: 0.0980

46248/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 384us/step - acc: 0.9703 - loss: 0.0980

46387/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 384us/step - acc: 0.9703 - loss: 0.0980

46521/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 384us/step - acc: 0.9703 - loss: 0.0980

46660/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 384us/step - acc: 0.9703 - loss: 0.0980

46796/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 384us/step - acc: 0.9703 - loss: 0.0981

46933/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 384us/step - acc: 0.9703 - loss: 0.0981

47071/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 384us/step - acc: 0.9702 - loss: 0.0981

47208/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 384us/step - acc: 0.9702 - loss: 0.0981

47345/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 384us/step - acc: 0.9702 - loss: 0.0981

47483/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 384us/step - acc: 0.9702 - loss: 0.0981

47620/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 384us/step - acc: 0.9702 - loss: 0.0982

47758/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 384us/step - acc: 0.9702 - loss: 0.0982

47896/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 384us/step - acc: 0.9702 - loss: 0.0982

48035/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 384us/step - acc: 0.9702 - loss: 0.0982

48169/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 384us/step - acc: 0.9702 - loss: 0.0982

48303/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9702 - loss: 0.0982

48440/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9702 - loss: 0.0983

48574/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9702 - loss: 0.0983

48712/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9702 - loss: 0.0983

48850/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9702 - loss: 0.0983

48986/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9702 - loss: 0.0983

49124/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9701 - loss: 0.0983

49262/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9701 - loss: 0.0984

49400/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9701 - loss: 0.0984

49531/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9701 - loss: 0.0984

49668/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9701 - loss: 0.0984

49804/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9701 - loss: 0.0984

49938/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9701 - loss: 0.0984

50073/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9701 - loss: 0.0985

50209/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9701 - loss: 0.0985

50344/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9701 - loss: 0.0985

50481/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9701 - loss: 0.0985

50619/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9701 - loss: 0.0985

50758/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9701 - loss: 0.0985

50894/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9701 - loss: 0.0985

51031/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9701 - loss: 0.0986

51160/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9701 - loss: 0.0986

51294/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9701 - loss: 0.0986

51432/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9701 - loss: 0.0986

51563/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9700 - loss: 0.0986

51697/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9700 - loss: 0.0986

51835/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9700 - loss: 0.0986

51975/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9700 - loss: 0.0986

52104/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9700 - loss: 0.0987

52130/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9700 - loss: 0.0987

52227/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 384us/step - acc: 0.9700 - loss: 0.0987

52350/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 384us/step - acc: 0.9700 - loss: 0.0987

52472/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 384us/step - acc: 0.9700 - loss: 0.0987

52600/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 384us/step - acc: 0.9700 - loss: 0.0987

52736/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 384us/step - acc: 0.9700 - loss: 0.0987

52867/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 384us/step - acc: 0.9700 - loss: 0.0987

53000/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 384us/step - acc: 0.9700 - loss: 0.0988

53136/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 384us/step - acc: 0.9700 - loss: 0.0988

53274/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 384us/step - acc: 0.9700 - loss: 0.0988

53407/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 384us/step - acc: 0.9700 - loss: 0.0988

53538/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 384us/step - acc: 0.9700 - loss: 0.0988

53663/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 384us/step - acc: 0.9700 - loss: 0.0988

53799/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 384us/step - acc: 0.9700 - loss: 0.0988

53933/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 383us/step - acc: 0.9700 - loss: 0.0989

54062/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 384us/step - acc: 0.9700 - loss: 0.0989

54200/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 383us/step - acc: 0.9699 - loss: 0.0989

54338/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 383us/step - acc: 0.9699 - loss: 0.0989

54476/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 383us/step - acc: 0.9699 - loss: 0.0989

54615/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 383us/step - acc: 0.9699 - loss: 0.0989

54748/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 383us/step - acc: 0.9699 - loss: 0.0989

54883/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 383us/step - acc: 0.9699 - loss: 0.0990

55012/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 383us/step - acc: 0.9699 - loss: 0.0990

55151/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 383us/step - acc: 0.9699 - loss: 0.0990

55277/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 383us/step - acc: 0.9699 - loss: 0.0990

55385/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 383us/step - acc: 0.9699 - loss: 0.0990

55502/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 383us/step - acc: 0.9699 - loss: 0.0990

55618/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9699 - loss: 0.0990

55736/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9699 - loss: 0.0990

55862/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9699 - loss: 0.0990

55984/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9699 - loss: 0.0991

56103/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9699 - loss: 0.0991

56228/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9699 - loss: 0.0991

56347/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9699 - loss: 0.0991

56467/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9699 - loss: 0.0991

56589/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9699 - loss: 0.0991

56716/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9699 - loss: 0.0991

56836/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9699 - loss: 0.0991

56963/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9699 - loss: 0.0991

57093/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9698 - loss: 0.0991

57219/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9698 - loss: 0.0992

57342/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9698 - loss: 0.0992

57457/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 384us/step - acc: 0.9698 - loss: 0.0992

57571/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 385us/step - acc: 0.9698 - loss: 0.0992

57692/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 385us/step - acc: 0.9698 - loss: 0.0992

57812/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 385us/step - acc: 0.9698 - loss: 0.0992

57930/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 385us/step - acc: 0.9698 - loss: 0.0992

58046/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 385us/step - acc: 0.9698 - loss: 0.0992

58160/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 385us/step - acc: 0.9698 - loss: 0.0992

58278/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 385us/step - acc: 0.9698 - loss: 0.0993

58392/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 385us/step - acc: 0.9698 - loss: 0.0993

58506/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 385us/step - acc: 0.9698 - loss: 0.0993

58619/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 385us/step - acc: 0.9698 - loss: 0.0993

58744/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 385us/step - acc: 0.9698 - loss: 0.0993

58865/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 385us/step - acc: 0.9698 - loss: 0.0993

58989/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 386us/step - acc: 0.9698 - loss: 0.0993

59109/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 386us/step - acc: 0.9698 - loss: 0.0993

59227/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 386us/step - acc: 0.9698 - loss: 0.0993

59341/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 386us/step - acc: 0.9698 - loss: 0.0993

59462/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 386us/step - acc: 0.9698 - loss: 0.0993

59583/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 386us/step - acc: 0.9698 - loss: 0.0994

59710/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 386us/step - acc: 0.9698 - loss: 0.0994

59840/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 386us/step - acc: 0.9698 - loss: 0.0994

59963/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 386us/step - acc: 0.9698 - loss: 0.0994

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 447us/step - acc: 0.9698 - loss: 0.0994 - val_acc: 0.9598 - val_loss: 0.1290

Epoch 4/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 13:50 14ms/step - acc: 1.0000 - loss: 0.3703

  110/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 460us/step - acc: 0.9737 - loss: 0.1116 

  224/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 449us/step - acc: 0.9702 - loss: 0.0943

  292/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 517us/step - acc: 0.9699 - loss: 0.0900

  407/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 495us/step - acc: 0.9710 - loss: 0.0849

  517/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 487us/step - acc: 0.9722 - loss: 0.0816

  635/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 475us/step - acc: 0.9735 - loss: 0.0784

  758/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 464us/step - acc: 0.9747 - loss: 0.0756

  880/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 457us/step - acc: 0.9755 - loss: 0.0733

  997/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 454us/step - acc: 0.9760 - loss: 0.0719

 1113/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 451us/step - acc: 0.9764 - loss: 0.0711

 1235/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 447us/step - acc: 0.9766 - loss: 0.0708

 1351/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 446us/step - acc: 0.9767 - loss: 0.0705

 1470/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 444us/step - acc: 0.9768 - loss: 0.0701

 1586/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 444us/step - acc: 0.9769 - loss: 0.0698

 1703/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 443us/step - acc: 0.9769 - loss: 0.0696

 1817/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 442us/step - acc: 0.9769 - loss: 0.0693

 1930/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 443us/step - acc: 0.9770 - loss: 0.0690

 2045/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 442us/step - acc: 0.9771 - loss: 0.0686

 2164/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 441us/step - acc: 0.9772 - loss: 0.0684

 2279/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 441us/step - acc: 0.9772 - loss: 0.0684

 2396/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 440us/step - acc: 0.9771 - loss: 0.0684

 2511/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 440us/step - acc: 0.9771 - loss: 0.0683

 2624/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 441us/step - acc: 0.9772 - loss: 0.0683

 2737/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 441us/step - acc: 0.9772 - loss: 0.0682

 2855/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 440us/step - acc: 0.9772 - loss: 0.0681

 2971/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 440us/step - acc: 0.9772 - loss: 0.0681

 3079/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 441us/step - acc: 0.9771 - loss: 0.0681

 3184/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 442us/step - acc: 0.9771 - loss: 0.0681

 3297/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 442us/step - acc: 0.9772 - loss: 0.0682

 3416/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 441us/step - acc: 0.9772 - loss: 0.0682

 3535/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 441us/step - acc: 0.9772 - loss: 0.0683

 3649/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 441us/step - acc: 0.9772 - loss: 0.0683

 3762/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 441us/step - acc: 0.9772 - loss: 0.0684

 3877/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 441us/step - acc: 0.9772 - loss: 0.0685

 3989/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 441us/step - acc: 0.9772 - loss: 0.0686

 4082/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 443us/step - acc: 0.9772 - loss: 0.0686

 4177/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 445us/step - acc: 0.9772 - loss: 0.0686

 4277/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 447us/step - acc: 0.9772 - loss: 0.0687

 4374/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 448us/step - acc: 0.9772 - loss: 0.0688

 4476/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 449us/step - acc: 0.9772 - loss: 0.0688

 4583/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 449us/step - acc: 0.9772 - loss: 0.0688

 4689/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 450us/step - acc: 0.9772 - loss: 0.0689

 4794/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 451us/step - acc: 0.9772 - loss: 0.0689

 4897/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 451us/step - acc: 0.9772 - loss: 0.0689

 5007/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 452us/step - acc: 0.9772 - loss: 0.0690

 5119/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 451us/step - acc: 0.9772 - loss: 0.0690

 5233/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 451us/step - acc: 0.9772 - loss: 0.0690

 5344/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 451us/step - acc: 0.9772 - loss: 0.0691

 5447/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 452us/step - acc: 0.9772 - loss: 0.0691

 5555/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 452us/step - acc: 0.9772 - loss: 0.0691

 5659/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 453us/step - acc: 0.9773 - loss: 0.0691

 5752/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 454us/step - acc: 0.9773 - loss: 0.0692

 5863/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 454us/step - acc: 0.9773 - loss: 0.0692

 5973/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 454us/step - acc: 0.9773 - loss: 0.0692

 6081/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 454us/step - acc: 0.9773 - loss: 0.0692

 6193/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 454us/step - acc: 0.9773 - loss: 0.0693

 6300/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 454us/step - acc: 0.9773 - loss: 0.0693

 6413/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 454us/step - acc: 0.9773 - loss: 0.0693

 6511/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 455us/step - acc: 0.9773 - loss: 0.0694

 6613/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 456us/step - acc: 0.9773 - loss: 0.0694

 6724/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 456us/step - acc: 0.9773 - loss: 0.0694

 6813/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 457us/step - acc: 0.9773 - loss: 0.0695

 6905/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 458us/step - acc: 0.9773 - loss: 0.0695

 7004/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 459us/step - acc: 0.9773 - loss: 0.0695

 7103/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 460us/step - acc: 0.9773 - loss: 0.0696

 7199/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 461us/step - acc: 0.9773 - loss: 0.0696

 7311/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 460us/step - acc: 0.9773 - loss: 0.0696

 7422/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 460us/step - acc: 0.9773 - loss: 0.0696

 7505/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 462us/step - acc: 0.9773 - loss: 0.0697

 7572/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 465us/step - acc: 0.9773 - loss: 0.0697

 7638/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 467us/step - acc: 0.9773 - loss: 0.0697

 7712/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 469us/step - acc: 0.9773 - loss: 0.0697

 7813/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 470us/step - acc: 0.9773 - loss: 0.0698

 7921/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 470us/step - acc: 0.9773 - loss: 0.0698

 8029/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 469us/step - acc: 0.9773 - loss: 0.0698

 8139/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 469us/step - acc: 0.9773 - loss: 0.0699

 8225/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 471us/step - acc: 0.9773 - loss: 0.0699

 8291/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 473us/step - acc: 0.9773 - loss: 0.0699

 8376/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 474us/step - acc: 0.9773 - loss: 0.0699

 8470/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 475us/step - acc: 0.9773 - loss: 0.0700

 8580/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 475us/step - acc: 0.9772 - loss: 0.0701

 8683/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 475us/step - acc: 0.9772 - loss: 0.0701

 8781/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 475us/step - acc: 0.9772 - loss: 0.0702

 8878/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 476us/step - acc: 0.9772 - loss: 0.0703

 8978/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 476us/step - acc: 0.9772 - loss: 0.0703

 9072/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 476us/step - acc: 0.9771 - loss: 0.0704

 9177/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 477us/step - acc: 0.9771 - loss: 0.0705

 9268/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 477us/step - acc: 0.9771 - loss: 0.0706

 9372/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 477us/step - acc: 0.9771 - loss: 0.0706

 9468/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 478us/step - acc: 0.9770 - loss: 0.0707

 9547/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 479us/step - acc: 0.9770 - loss: 0.0707

 9652/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 479us/step - acc: 0.9770 - loss: 0.0708

 9761/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 479us/step - acc: 0.9770 - loss: 0.0709

 9873/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 479us/step - acc: 0.9770 - loss: 0.0709

 9960/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 479us/step - acc: 0.9770 - loss: 0.0710

10059/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 480us/step - acc: 0.9769 - loss: 0.0711

10145/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 481us/step - acc: 0.9769 - loss: 0.0711

10238/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 481us/step - acc: 0.9769 - loss: 0.0712

10334/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 482us/step - acc: 0.9769 - loss: 0.0713

10440/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 481us/step - acc: 0.9769 - loss: 0.0713

10553/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 481us/step - acc: 0.9768 - loss: 0.0714

10646/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 482us/step - acc: 0.9768 - loss: 0.0714

10732/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 482us/step - acc: 0.9768 - loss: 0.0715

10836/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 482us/step - acc: 0.9768 - loss: 0.0715

10943/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 482us/step - acc: 0.9768 - loss: 0.0716

11059/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 482us/step - acc: 0.9768 - loss: 0.0716

11167/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 482us/step - acc: 0.9767 - loss: 0.0717

11279/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 481us/step - acc: 0.9767 - loss: 0.0718

11388/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 481us/step - acc: 0.9767 - loss: 0.0718

11494/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 481us/step - acc: 0.9767 - loss: 0.0719

11608/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 481us/step - acc: 0.9767 - loss: 0.0720

11718/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 480us/step - acc: 0.9766 - loss: 0.0720

11823/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 480us/step - acc: 0.9766 - loss: 0.0721

11934/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 480us/step - acc: 0.9766 - loss: 0.0721

12025/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 481us/step - acc: 0.9766 - loss: 0.0722

12130/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 481us/step - acc: 0.9766 - loss: 0.0722

12226/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 481us/step - acc: 0.9766 - loss: 0.0723

12314/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 482us/step - acc: 0.9765 - loss: 0.0723

12405/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 482us/step - acc: 0.9765 - loss: 0.0724

12507/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 482us/step - acc: 0.9765 - loss: 0.0724

12623/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 482us/step - acc: 0.9765 - loss: 0.0725

12729/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 482us/step - acc: 0.9765 - loss: 0.0726

12843/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 481us/step - acc: 0.9765 - loss: 0.0726

12959/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 481us/step - acc: 0.9764 - loss: 0.0727

13076/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 480us/step - acc: 0.9764 - loss: 0.0727

13191/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 480us/step - acc: 0.9764 - loss: 0.0728

13298/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 480us/step - acc: 0.9764 - loss: 0.0729

13413/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 480us/step - acc: 0.9763 - loss: 0.0729

13510/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 480us/step - acc: 0.9763 - loss: 0.0730

13620/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 480us/step - acc: 0.9763 - loss: 0.0730

13734/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 479us/step - acc: 0.9763 - loss: 0.0731

13845/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 479us/step - acc: 0.9763 - loss: 0.0731

13956/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 479us/step - acc: 0.9763 - loss: 0.0732

14014/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 481us/step - acc: 0.9762 - loss: 0.0732

14084/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 482us/step - acc: 0.9762 - loss: 0.0732

14175/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 482us/step - acc: 0.9762 - loss: 0.0733

14217/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 484us/step - acc: 0.9762 - loss: 0.0733

14308/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 485us/step - acc: 0.9762 - loss: 0.0733

14419/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 485us/step - acc: 0.9762 - loss: 0.0734

14526/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 484us/step - acc: 0.9762 - loss: 0.0734

14641/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 484us/step - acc: 0.9761 - loss: 0.0735

14744/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 484us/step - acc: 0.9761 - loss: 0.0735

14858/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 484us/step - acc: 0.9761 - loss: 0.0736

14970/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 483us/step - acc: 0.9761 - loss: 0.0736

15086/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 483us/step - acc: 0.9761 - loss: 0.0737

15201/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 483us/step - acc: 0.9761 - loss: 0.0738

15321/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 482us/step - acc: 0.9760 - loss: 0.0738

15435/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 482us/step - acc: 0.9760 - loss: 0.0739

15546/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 482us/step - acc: 0.9760 - loss: 0.0739

15658/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 481us/step - acc: 0.9760 - loss: 0.0740

15784/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 481us/step - acc: 0.9760 - loss: 0.0740

15906/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 480us/step - acc: 0.9760 - loss: 0.0741

16032/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 480us/step - acc: 0.9759 - loss: 0.0741

16158/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 479us/step - acc: 0.9759 - loss: 0.0742

16263/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 479us/step - acc: 0.9759 - loss: 0.0742

16371/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 479us/step - acc: 0.9759 - loss: 0.0742

16461/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 479us/step - acc: 0.9759 - loss: 0.0743

16532/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 480us/step - acc: 0.9759 - loss: 0.0743

16613/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 481us/step - acc: 0.9759 - loss: 0.0743

16703/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 481us/step - acc: 0.9759 - loss: 0.0744

16789/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 482us/step - acc: 0.9759 - loss: 0.0744

16899/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 482us/step - acc: 0.9758 - loss: 0.0744

17001/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 482us/step - acc: 0.9758 - loss: 0.0744

17111/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 482us/step - acc: 0.9758 - loss: 0.0745

17232/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 481us/step - acc: 0.9758 - loss: 0.0745

17339/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 481us/step - acc: 0.9758 - loss: 0.0745

17421/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 482us/step - acc: 0.9758 - loss: 0.0746

17515/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 482us/step - acc: 0.9758 - loss: 0.0746

17619/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 482us/step - acc: 0.9758 - loss: 0.0746

17714/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 482us/step - acc: 0.9758 - loss: 0.0746

17803/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 483us/step - acc: 0.9758 - loss: 0.0747

17882/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 483us/step - acc: 0.9758 - loss: 0.0747

17985/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 483us/step - acc: 0.9758 - loss: 0.0747

18100/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 483us/step - acc: 0.9757 - loss: 0.0747

18215/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 483us/step - acc: 0.9757 - loss: 0.0748

18335/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 482us/step - acc: 0.9757 - loss: 0.0748

18455/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 482us/step - acc: 0.9757 - loss: 0.0748

18570/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 482us/step - acc: 0.9757 - loss: 0.0749

18690/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 481us/step - acc: 0.9757 - loss: 0.0749

18809/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 481us/step - acc: 0.9757 - loss: 0.0749

18923/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 481us/step - acc: 0.9757 - loss: 0.0750

19033/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 481us/step - acc: 0.9757 - loss: 0.0750

19134/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 481us/step - acc: 0.9757 - loss: 0.0750

19250/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 480us/step - acc: 0.9757 - loss: 0.0750

19357/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 480us/step - acc: 0.9757 - loss: 0.0751

19476/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 480us/step - acc: 0.9756 - loss: 0.0751

19591/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 480us/step - acc: 0.9756 - loss: 0.0751

19697/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 480us/step - acc: 0.9756 - loss: 0.0751

19799/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 480us/step - acc: 0.9756 - loss: 0.0752

19910/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 480us/step - acc: 0.9756 - loss: 0.0752

20029/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 479us/step - acc: 0.9756 - loss: 0.0752

20146/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 479us/step - acc: 0.9756 - loss: 0.0753

20261/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 479us/step - acc: 0.9756 - loss: 0.0753

20373/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 479us/step - acc: 0.9756 - loss: 0.0753

20490/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 478us/step - acc: 0.9756 - loss: 0.0753

20610/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 478us/step - acc: 0.9756 - loss: 0.0754

20724/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 478us/step - acc: 0.9756 - loss: 0.0754

20835/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 478us/step - acc: 0.9756 - loss: 0.0754

20949/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 477us/step - acc: 0.9756 - loss: 0.0754

21062/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 477us/step - acc: 0.9756 - loss: 0.0755

21169/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 477us/step - acc: 0.9755 - loss: 0.0755

21280/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 477us/step - acc: 0.9755 - loss: 0.0755

21379/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 477us/step - acc: 0.9755 - loss: 0.0755

21496/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 477us/step - acc: 0.9755 - loss: 0.0756

21618/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 477us/step - acc: 0.9755 - loss: 0.0756

21737/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 476us/step - acc: 0.9755 - loss: 0.0756

21844/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 476us/step - acc: 0.9755 - loss: 0.0756

21933/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 477us/step - acc: 0.9755 - loss: 0.0756

22030/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 477us/step - acc: 0.9755 - loss: 0.0757

22116/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 477us/step - acc: 0.9755 - loss: 0.0757

22208/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 477us/step - acc: 0.9755 - loss: 0.0757

22308/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 478us/step - acc: 0.9755 - loss: 0.0757

22400/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 478us/step - acc: 0.9755 - loss: 0.0757

22496/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 478us/step - acc: 0.9755 - loss: 0.0758

22560/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 479us/step - acc: 0.9755 - loss: 0.0758

22622/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 480us/step - acc: 0.9755 - loss: 0.0758

22673/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 481us/step - acc: 0.9755 - loss: 0.0758

22725/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 482us/step - acc: 0.9755 - loss: 0.0758

22761/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 484us/step - acc: 0.9755 - loss: 0.0758

22796/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 485us/step - acc: 0.9755 - loss: 0.0758

22840/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 486us/step - acc: 0.9755 - loss: 0.0758

22919/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 487us/step - acc: 0.9755 - loss: 0.0759

22972/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 488us/step - acc: 0.9755 - loss: 0.0759

23068/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 488us/step - acc: 0.9755 - loss: 0.0759

23155/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 488us/step - acc: 0.9755 - loss: 0.0759

23252/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 489us/step - acc: 0.9755 - loss: 0.0759

23351/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 489us/step - acc: 0.9755 - loss: 0.0759

23448/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 489us/step - acc: 0.9755 - loss: 0.0760

23556/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 489us/step - acc: 0.9755 - loss: 0.0760

23669/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 488us/step - acc: 0.9754 - loss: 0.0760

23776/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 488us/step - acc: 0.9754 - loss: 0.0760

23880/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 488us/step - acc: 0.9754 - loss: 0.0760

23991/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 488us/step - acc: 0.9754 - loss: 0.0761

24098/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 488us/step - acc: 0.9754 - loss: 0.0761

24206/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 488us/step - acc: 0.9754 - loss: 0.0761

24324/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 488us/step - acc: 0.9754 - loss: 0.0761

24447/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 487us/step - acc: 0.9754 - loss: 0.0762

24569/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 487us/step - acc: 0.9754 - loss: 0.0762

24683/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 487us/step - acc: 0.9754 - loss: 0.0762

24804/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 486us/step - acc: 0.9754 - loss: 0.0762

24923/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 486us/step - acc: 0.9754 - loss: 0.0763

25038/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 486us/step - acc: 0.9754 - loss: 0.0763

25157/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 486us/step - acc: 0.9754 - loss: 0.0763

25283/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 485us/step - acc: 0.9754 - loss: 0.0763

25413/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 485us/step - acc: 0.9754 - loss: 0.0764

25543/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 484us/step - acc: 0.9754 - loss: 0.0764

25653/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 484us/step - acc: 0.9754 - loss: 0.0764

25703/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 485us/step - acc: 0.9754 - loss: 0.0764

25820/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 485us/step - acc: 0.9754 - loss: 0.0764

25933/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 485us/step - acc: 0.9754 - loss: 0.0765

26059/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 484us/step - acc: 0.9753 - loss: 0.0765

26181/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 484us/step - acc: 0.9753 - loss: 0.0765

26302/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 484us/step - acc: 0.9753 - loss: 0.0765

26423/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 483us/step - acc: 0.9753 - loss: 0.0766

26542/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 483us/step - acc: 0.9753 - loss: 0.0766

26673/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 482us/step - acc: 0.9753 - loss: 0.0766

26807/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 482us/step - acc: 0.9753 - loss: 0.0766

26946/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 481us/step - acc: 0.9753 - loss: 0.0767

27089/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 481us/step - acc: 0.9753 - loss: 0.0767

27225/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 480us/step - acc: 0.9753 - loss: 0.0767

27357/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 480us/step - acc: 0.9753 - loss: 0.0767

27499/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 479us/step - acc: 0.9753 - loss: 0.0768

27636/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 478us/step - acc: 0.9753 - loss: 0.0768

27776/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 478us/step - acc: 0.9753 - loss: 0.0768

27917/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 477us/step - acc: 0.9753 - loss: 0.0768

28056/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 477us/step - acc: 0.9753 - loss: 0.0769

28196/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 476us/step - acc: 0.9753 - loss: 0.0769

28334/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 475us/step - acc: 0.9753 - loss: 0.0769

28477/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 475us/step - acc: 0.9753 - loss: 0.0769

28606/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 474us/step - acc: 0.9753 - loss: 0.0770

28737/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 474us/step - acc: 0.9753 - loss: 0.0770

28875/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 474us/step - acc: 0.9753 - loss: 0.0770

29004/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 473us/step - acc: 0.9753 - loss: 0.0770

29133/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 473us/step - acc: 0.9752 - loss: 0.0771

29271/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 472us/step - acc: 0.9752 - loss: 0.0771

29407/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 472us/step - acc: 0.9752 - loss: 0.0771

29542/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 471us/step - acc: 0.9752 - loss: 0.0771

29673/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 471us/step - acc: 0.9752 - loss: 0.0772

29793/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 471us/step - acc: 0.9752 - loss: 0.0772

29913/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 470us/step - acc: 0.9752 - loss: 0.0772

30048/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 470us/step - acc: 0.9752 - loss: 0.0772

30176/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 470us/step - acc: 0.9752 - loss: 0.0772

30312/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 469us/step - acc: 0.9752 - loss: 0.0773

30449/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 469us/step - acc: 0.9752 - loss: 0.0773

30584/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 468us/step - acc: 0.9752 - loss: 0.0773

30718/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 468us/step - acc: 0.9752 - loss: 0.0773

30846/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 468us/step - acc: 0.9752 - loss: 0.0774

30979/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 467us/step - acc: 0.9752 - loss: 0.0774

31109/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 467us/step - acc: 0.9752 - loss: 0.0774

31244/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 466us/step - acc: 0.9752 - loss: 0.0774

31379/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 466us/step - acc: 0.9752 - loss: 0.0774

31509/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 466us/step - acc: 0.9752 - loss: 0.0775

31646/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 465us/step - acc: 0.9752 - loss: 0.0775

31787/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 465us/step - acc: 0.9752 - loss: 0.0775

31923/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 464us/step - acc: 0.9752 - loss: 0.0775

32048/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 464us/step - acc: 0.9752 - loss: 0.0775

32180/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 464us/step - acc: 0.9752 - loss: 0.0776

32316/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 463us/step - acc: 0.9751 - loss: 0.0776

32454/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 463us/step - acc: 0.9751 - loss: 0.0776

32590/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 463us/step - acc: 0.9751 - loss: 0.0776

32728/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 462us/step - acc: 0.9751 - loss: 0.0777

32866/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 462us/step - acc: 0.9751 - loss: 0.0777

33001/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 461us/step - acc: 0.9751 - loss: 0.0777

33138/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 461us/step - acc: 0.9751 - loss: 0.0777

33277/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 461us/step - acc: 0.9751 - loss: 0.0778

33419/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 460us/step - acc: 0.9751 - loss: 0.0778

33556/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 460us/step - acc: 0.9751 - loss: 0.0778

33696/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 459us/step - acc: 0.9751 - loss: 0.0778

33834/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 459us/step - acc: 0.9751 - loss: 0.0779

33961/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 459us/step - acc: 0.9751 - loss: 0.0779

34097/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 458us/step - acc: 0.9751 - loss: 0.0779

34234/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 458us/step - acc: 0.9751 - loss: 0.0779

34374/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 458us/step - acc: 0.9751 - loss: 0.0780

34513/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 457us/step - acc: 0.9751 - loss: 0.0780

34648/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 457us/step - acc: 0.9751 - loss: 0.0780

34777/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 457us/step - acc: 0.9751 - loss: 0.0780

34911/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 456us/step - acc: 0.9750 - loss: 0.0781

35045/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 456us/step - acc: 0.9750 - loss: 0.0781

35183/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 456us/step - acc: 0.9750 - loss: 0.0781

35318/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 455us/step - acc: 0.9750 - loss: 0.0781

35451/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 455us/step - acc: 0.9750 - loss: 0.0782

35588/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 455us/step - acc: 0.9750 - loss: 0.0782

35725/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 454us/step - acc: 0.9750 - loss: 0.0782

35862/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 454us/step - acc: 0.9750 - loss: 0.0782

35999/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 454us/step - acc: 0.9750 - loss: 0.0783

36138/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 453us/step - acc: 0.9750 - loss: 0.0783

36275/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 453us/step - acc: 0.9750 - loss: 0.0783

36413/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 453us/step - acc: 0.9750 - loss: 0.0783

36550/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 452us/step - acc: 0.9750 - loss: 0.0784

36689/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 452us/step - acc: 0.9750 - loss: 0.0784

36828/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 452us/step - acc: 0.9750 - loss: 0.0784

36968/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 451us/step - acc: 0.9750 - loss: 0.0784

37099/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 451us/step - acc: 0.9750 - loss: 0.0785

37234/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 451us/step - acc: 0.9750 - loss: 0.0785

37367/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 450us/step - acc: 0.9750 - loss: 0.0785

37495/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 450us/step - acc: 0.9749 - loss: 0.0785

37628/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 450us/step - acc: 0.9749 - loss: 0.0786

37767/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 450us/step - acc: 0.9749 - loss: 0.0786 

37899/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 449us/step - acc: 0.9749 - loss: 0.0786

38039/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 449us/step - acc: 0.9749 - loss: 0.0786

38171/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 449us/step - acc: 0.9749 - loss: 0.0786

38306/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 449us/step - acc: 0.9749 - loss: 0.0787

38445/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 448us/step - acc: 0.9749 - loss: 0.0787

38581/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 448us/step - acc: 0.9749 - loss: 0.0787

38719/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 448us/step - acc: 0.9749 - loss: 0.0787

38858/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 447us/step - acc: 0.9749 - loss: 0.0788

38994/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 447us/step - acc: 0.9749 - loss: 0.0788

39124/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 447us/step - acc: 0.9749 - loss: 0.0788

39262/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 447us/step - acc: 0.9749 - loss: 0.0788

39402/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 446us/step - acc: 0.9749 - loss: 0.0789

39538/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 446us/step - acc: 0.9749 - loss: 0.0789

39677/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 446us/step - acc: 0.9749 - loss: 0.0789

39816/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 445us/step - acc: 0.9749 - loss: 0.0789

39953/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 445us/step - acc: 0.9749 - loss: 0.0790

40090/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 445us/step - acc: 0.9749 - loss: 0.0790

40219/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 445us/step - acc: 0.9749 - loss: 0.0790

40358/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 444us/step - acc: 0.9748 - loss: 0.0790

40495/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 444us/step - acc: 0.9748 - loss: 0.0790

40627/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 444us/step - acc: 0.9748 - loss: 0.0791

40759/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 444us/step - acc: 0.9748 - loss: 0.0791

40891/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 444us/step - acc: 0.9748 - loss: 0.0791

41028/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 443us/step - acc: 0.9748 - loss: 0.0791

41160/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 443us/step - acc: 0.9748 - loss: 0.0792

41297/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 443us/step - acc: 0.9748 - loss: 0.0792

41434/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 443us/step - acc: 0.9748 - loss: 0.0792

41571/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 442us/step - acc: 0.9748 - loss: 0.0792

41707/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 442us/step - acc: 0.9748 - loss: 0.0792

41844/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 442us/step - acc: 0.9748 - loss: 0.0793

41983/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 442us/step - acc: 0.9748 - loss: 0.0793

42120/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 441us/step - acc: 0.9748 - loss: 0.0793

42247/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 441us/step - acc: 0.9748 - loss: 0.0793

42387/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 441us/step - acc: 0.9748 - loss: 0.0793

42526/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 441us/step - acc: 0.9748 - loss: 0.0794

42666/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 440us/step - acc: 0.9748 - loss: 0.0794

42803/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 440us/step - acc: 0.9748 - loss: 0.0794

42942/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 440us/step - acc: 0.9748 - loss: 0.0794

43080/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 440us/step - acc: 0.9748 - loss: 0.0794

43216/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 439us/step - acc: 0.9748 - loss: 0.0795

43354/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 439us/step - acc: 0.9748 - loss: 0.0795

43492/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 439us/step - acc: 0.9747 - loss: 0.0795

43625/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 439us/step - acc: 0.9747 - loss: 0.0795

43764/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 439us/step - acc: 0.9747 - loss: 0.0795

43903/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 438us/step - acc: 0.9747 - loss: 0.0796

44041/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 438us/step - acc: 0.9747 - loss: 0.0796

44178/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 438us/step - acc: 0.9747 - loss: 0.0796

44314/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 438us/step - acc: 0.9747 - loss: 0.0796

44453/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 437us/step - acc: 0.9747 - loss: 0.0796

44590/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 437us/step - acc: 0.9747 - loss: 0.0797

44717/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 437us/step - acc: 0.9747 - loss: 0.0797

44855/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 437us/step - acc: 0.9747 - loss: 0.0797

44993/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 437us/step - acc: 0.9747 - loss: 0.0797

45131/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 436us/step - acc: 0.9747 - loss: 0.0797

45270/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 436us/step - acc: 0.9747 - loss: 0.0798

45407/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 436us/step - acc: 0.9747 - loss: 0.0798

45544/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 436us/step - acc: 0.9747 - loss: 0.0798

45682/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 436us/step - acc: 0.9747 - loss: 0.0798

45820/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 435us/step - acc: 0.9747 - loss: 0.0798

45958/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 435us/step - acc: 0.9747 - loss: 0.0798

46096/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 435us/step - acc: 0.9747 - loss: 0.0799

46234/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 435us/step - acc: 0.9747 - loss: 0.0799

46367/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 434us/step - acc: 0.9747 - loss: 0.0799

46501/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 434us/step - acc: 0.9747 - loss: 0.0799

46639/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 434us/step - acc: 0.9747 - loss: 0.0799

46778/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 434us/step - acc: 0.9747 - loss: 0.0799

46915/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 434us/step - acc: 0.9747 - loss: 0.0800

47049/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 434us/step - acc: 0.9747 - loss: 0.0800

47186/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 433us/step - acc: 0.9747 - loss: 0.0800

47322/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 433us/step - acc: 0.9747 - loss: 0.0800

47459/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 433us/step - acc: 0.9746 - loss: 0.0800

47597/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 433us/step - acc: 0.9746 - loss: 0.0800

47731/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 433us/step - acc: 0.9746 - loss: 0.0801

47856/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 433us/step - acc: 0.9746 - loss: 0.0801

47990/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 432us/step - acc: 0.9746 - loss: 0.0801

48126/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 432us/step - acc: 0.9746 - loss: 0.0801

48264/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 432us/step - acc: 0.9746 - loss: 0.0801

48399/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 432us/step - acc: 0.9746 - loss: 0.0801

48533/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 432us/step - acc: 0.9746 - loss: 0.0801

48672/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 431us/step - acc: 0.9746 - loss: 0.0802

48809/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 431us/step - acc: 0.9746 - loss: 0.0802

48948/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 431us/step - acc: 0.9746 - loss: 0.0802

49085/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 431us/step - acc: 0.9746 - loss: 0.0802

49226/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 431us/step - acc: 0.9746 - loss: 0.0802

49366/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 430us/step - acc: 0.9746 - loss: 0.0802

49499/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 430us/step - acc: 0.9746 - loss: 0.0803

49622/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 430us/step - acc: 0.9746 - loss: 0.0803

49742/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 430us/step - acc: 0.9746 - loss: 0.0803

49870/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 430us/step - acc: 0.9746 - loss: 0.0803

49995/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 430us/step - acc: 0.9746 - loss: 0.0803

50120/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 430us/step - acc: 0.9746 - loss: 0.0803

50242/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 430us/step - acc: 0.9746 - loss: 0.0803

50373/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 430us/step - acc: 0.9746 - loss: 0.0804

50507/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 430us/step - acc: 0.9746 - loss: 0.0804

50641/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 430us/step - acc: 0.9746 - loss: 0.0804

50778/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 429us/step - acc: 0.9746 - loss: 0.0804

50918/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 429us/step - acc: 0.9746 - loss: 0.0804

51057/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 429us/step - acc: 0.9746 - loss: 0.0804

51195/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 429us/step - acc: 0.9746 - loss: 0.0804

51332/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 429us/step - acc: 0.9746 - loss: 0.0805

51466/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 428us/step - acc: 0.9746 - loss: 0.0805

51604/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 428us/step - acc: 0.9746 - loss: 0.0805

51743/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 428us/step - acc: 0.9746 - loss: 0.0805

51875/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 428us/step - acc: 0.9746 - loss: 0.0805

52001/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 428us/step - acc: 0.9746 - loss: 0.0805

52135/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 428us/step - acc: 0.9745 - loss: 0.0806

52270/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 428us/step - acc: 0.9745 - loss: 0.0806

52407/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 428us/step - acc: 0.9745 - loss: 0.0806

52545/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 427us/step - acc: 0.9745 - loss: 0.0806

52687/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 427us/step - acc: 0.9745 - loss: 0.0806

52828/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 427us/step - acc: 0.9745 - loss: 0.0806

52966/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 427us/step - acc: 0.9745 - loss: 0.0806

53105/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 427us/step - acc: 0.9745 - loss: 0.0807

53244/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 426us/step - acc: 0.9745 - loss: 0.0807

53381/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 426us/step - acc: 0.9745 - loss: 0.0807

53518/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 426us/step - acc: 0.9745 - loss: 0.0807

53657/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 426us/step - acc: 0.9745 - loss: 0.0807

53793/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 426us/step - acc: 0.9745 - loss: 0.0807

53933/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 426us/step - acc: 0.9745 - loss: 0.0808

54058/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 426us/step - acc: 0.9745 - loss: 0.0808

54183/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 426us/step - acc: 0.9745 - loss: 0.0808

54310/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 425us/step - acc: 0.9745 - loss: 0.0808

54435/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 425us/step - acc: 0.9745 - loss: 0.0808

54534/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 426us/step - acc: 0.9745 - loss: 0.0808

54653/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 426us/step - acc: 0.9745 - loss: 0.0808

54765/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 426us/step - acc: 0.9745 - loss: 0.0809

54870/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 426us/step - acc: 0.9745 - loss: 0.0809

54964/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 426us/step - acc: 0.9745 - loss: 0.0809

55076/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 426us/step - acc: 0.9745 - loss: 0.0809

55179/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 426us/step - acc: 0.9745 - loss: 0.0809

55300/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 426us/step - acc: 0.9745 - loss: 0.0809

55412/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 426us/step - acc: 0.9745 - loss: 0.0809

55533/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 426us/step - acc: 0.9745 - loss: 0.0809

55660/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 426us/step - acc: 0.9745 - loss: 0.0809

55786/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 426us/step - acc: 0.9745 - loss: 0.0810

55917/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 426us/step - acc: 0.9745 - loss: 0.0810

56053/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 426us/step - acc: 0.9745 - loss: 0.0810

56191/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 426us/step - acc: 0.9745 - loss: 0.0810

56330/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9744 - loss: 0.0810

56470/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9744 - loss: 0.0810

56608/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9744 - loss: 0.0811

56740/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9744 - loss: 0.0811

56875/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9744 - loss: 0.0811

57009/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9744 - loss: 0.0811

57136/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9744 - loss: 0.0811

57274/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 424us/step - acc: 0.9744 - loss: 0.0811

57413/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 424us/step - acc: 0.9744 - loss: 0.0811

57551/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 424us/step - acc: 0.9744 - loss: 0.0812

57689/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 424us/step - acc: 0.9744 - loss: 0.0812

57827/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 424us/step - acc: 0.9744 - loss: 0.0812

57966/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 424us/step - acc: 0.9744 - loss: 0.0812

58106/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 424us/step - acc: 0.9744 - loss: 0.0812

58244/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 423us/step - acc: 0.9744 - loss: 0.0812

58384/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 423us/step - acc: 0.9744 - loss: 0.0812

58521/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 423us/step - acc: 0.9744 - loss: 0.0813

58659/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 423us/step - acc: 0.9744 - loss: 0.0813

58801/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 423us/step - acc: 0.9744 - loss: 0.0813

58939/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 423us/step - acc: 0.9744 - loss: 0.0813

59077/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 423us/step - acc: 0.9744 - loss: 0.0813

59216/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 422us/step - acc: 0.9744 - loss: 0.0813

59357/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 422us/step - acc: 0.9744 - loss: 0.0814

59494/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 422us/step - acc: 0.9744 - loss: 0.0814

59632/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 422us/step - acc: 0.9744 - loss: 0.0814

59772/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 422us/step - acc: 0.9744 - loss: 0.0814

59911/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 422us/step - acc: 0.9744 - loss: 0.0814

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 483us/step - acc: 0.9744 - loss: 0.0814 - val_acc: 0.9580 - val_loss: 0.1335

Epoch 5/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 18:10 18ms/step - acc: 1.0000 - loss: 6.1749e-05

  115/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 442us/step - acc: 0.9671 - loss: 0.1208     

  228/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 443us/step - acc: 0.9714 - loss: 0.1019

  326/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 464us/step - acc: 0.9747 - loss: 0.0908

  442/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 456us/step - acc: 0.9769 - loss: 0.0836

  545/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 462us/step - acc: 0.9785 - loss: 0.0791

  634/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 477us/step - acc: 0.9794 - loss: 0.0768

  682/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 518us/step - acc: 0.9797 - loss: 0.0760

  730/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 552us/step - acc: 0.9800 - loss: 0.0752

  797/60000 ━━━━━━━━━━━━━━━━━━━━ 33s 569us/step - acc: 0.9802 - loss: 0.0746

  871/60000 ━━━━━━━━━━━━━━━━━━━━ 34s 578us/step - acc: 0.9802 - loss: 0.0741

  953/60000 ━━━━━━━━━━━━━━━━━━━━ 34s 581us/step - acc: 0.9800 - loss: 0.0742

 1059/60000 ━━━━━━━━━━━━━━━━━━━━ 33s 570us/step - acc: 0.9797 - loss: 0.0744

 1166/60000 ━━━━━━━━━━━━━━━━━━━━ 33s 561us/step - acc: 0.9796 - loss: 0.0745

 1281/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 550us/step - acc: 0.9796 - loss: 0.0745

 1393/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 542us/step - acc: 0.9797 - loss: 0.0742

 1504/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 535us/step - acc: 0.9798 - loss: 0.0740

 1624/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 527us/step - acc: 0.9798 - loss: 0.0738

 1737/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 521us/step - acc: 0.9797 - loss: 0.0737

 1856/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 515us/step - acc: 0.9796 - loss: 0.0738

 1952/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 515us/step - acc: 0.9796 - loss: 0.0739

 2016/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 524us/step - acc: 0.9795 - loss: 0.0741

 2081/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 532us/step - acc: 0.9795 - loss: 0.0742

 2106/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 549us/step - acc: 0.9795 - loss: 0.0743

 2166/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 557us/step - acc: 0.9794 - loss: 0.0744

 2222/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 566us/step - acc: 0.9794 - loss: 0.0746

 2300/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 569us/step - acc: 0.9793 - loss: 0.0749

 2382/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 570us/step - acc: 0.9793 - loss: 0.0751

 2467/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 571us/step - acc: 0.9792 - loss: 0.0752

 2563/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 569us/step - acc: 0.9792 - loss: 0.0753

 2652/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 569us/step - acc: 0.9792 - loss: 0.0754

 2750/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 567us/step - acc: 0.9791 - loss: 0.0755

 2852/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 564us/step - acc: 0.9791 - loss: 0.0756

 2966/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 559us/step - acc: 0.9790 - loss: 0.0757

 3037/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 563us/step - acc: 0.9790 - loss: 0.0757

 3097/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 568us/step - acc: 0.9790 - loss: 0.0757

 3175/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 570us/step - acc: 0.9790 - loss: 0.0757

 3267/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 570us/step - acc: 0.9790 - loss: 0.0757

 3348/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 571us/step - acc: 0.9789 - loss: 0.0757

 3466/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 566us/step - acc: 0.9789 - loss: 0.0757

 3583/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 561us/step - acc: 0.9789 - loss: 0.0757

 3700/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 557us/step - acc: 0.9788 - loss: 0.0757

 3819/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 553us/step - acc: 0.9787 - loss: 0.0757

 3942/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 548us/step - acc: 0.9787 - loss: 0.0757

 4065/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 544us/step - acc: 0.9786 - loss: 0.0758

 4193/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 540us/step - acc: 0.9785 - loss: 0.0758

 4325/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 535us/step - acc: 0.9785 - loss: 0.0758

 4433/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 533us/step - acc: 0.9785 - loss: 0.0758

 4521/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 534us/step - acc: 0.9784 - loss: 0.0758

 4606/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 535us/step - acc: 0.9784 - loss: 0.0757

 4713/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 534us/step - acc: 0.9784 - loss: 0.0757

 4831/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 531us/step - acc: 0.9784 - loss: 0.0756

 4950/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 528us/step - acc: 0.9784 - loss: 0.0755

 5070/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 526us/step - acc: 0.9784 - loss: 0.0755

 5172/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 525us/step - acc: 0.9784 - loss: 0.0754

 5298/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 522us/step - acc: 0.9784 - loss: 0.0753

 5425/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 519us/step - acc: 0.9784 - loss: 0.0753

 5546/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 517us/step - acc: 0.9784 - loss: 0.0752

 5668/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 515us/step - acc: 0.9784 - loss: 0.0752

 5794/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 512us/step - acc: 0.9783 - loss: 0.0751

 5904/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 511us/step - acc: 0.9783 - loss: 0.0751

 6003/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 511us/step - acc: 0.9783 - loss: 0.0752

 6106/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 511us/step - acc: 0.9782 - loss: 0.0752

 6217/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 510us/step - acc: 0.9782 - loss: 0.0752

 6326/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 509us/step - acc: 0.9782 - loss: 0.0753

 6433/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 508us/step - acc: 0.9782 - loss: 0.0753

 6549/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 507us/step - acc: 0.9781 - loss: 0.0754

 6674/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 505us/step - acc: 0.9781 - loss: 0.0754

 6810/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 502us/step - acc: 0.9781 - loss: 0.0754

 6935/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 500us/step - acc: 0.9780 - loss: 0.0755

 7058/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 499us/step - acc: 0.9780 - loss: 0.0755

 7161/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 498us/step - acc: 0.9780 - loss: 0.0755

 7283/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 497us/step - acc: 0.9780 - loss: 0.0755

 7417/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 495us/step - acc: 0.9779 - loss: 0.0756

 7555/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 492us/step - acc: 0.9779 - loss: 0.0756

 7685/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 491us/step - acc: 0.9779 - loss: 0.0756

 7817/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 489us/step - acc: 0.9779 - loss: 0.0756

 7950/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 487us/step - acc: 0.9779 - loss: 0.0756

 8084/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 485us/step - acc: 0.9778 - loss: 0.0756

 8207/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 484us/step - acc: 0.9778 - loss: 0.0756

 8314/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 484us/step - acc: 0.9778 - loss: 0.0756

 8432/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 483us/step - acc: 0.9778 - loss: 0.0756

 8550/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 482us/step - acc: 0.9778 - loss: 0.0755

 8678/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 481us/step - acc: 0.9778 - loss: 0.0755

 8791/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 480us/step - acc: 0.9778 - loss: 0.0755

 8916/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 479us/step - acc: 0.9777 - loss: 0.0755

 9023/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 479us/step - acc: 0.9777 - loss: 0.0755

 9124/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 479us/step - acc: 0.9777 - loss: 0.0754

 9239/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 479us/step - acc: 0.9777 - loss: 0.0754

 9362/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 478us/step - acc: 0.9777 - loss: 0.0754

 9480/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 477us/step - acc: 0.9777 - loss: 0.0753

 9581/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 477us/step - acc: 0.9777 - loss: 0.0753

 9686/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 477us/step - acc: 0.9777 - loss: 0.0753

 9743/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 480us/step - acc: 0.9777 - loss: 0.0752

 9817/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 481us/step - acc: 0.9777 - loss: 0.0752

 9913/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 482us/step - acc: 0.9777 - loss: 0.0752

10017/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 482us/step - acc: 0.9777 - loss: 0.0751

10125/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 482us/step - acc: 0.9777 - loss: 0.0751

10220/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 482us/step - acc: 0.9777 - loss: 0.0750

10315/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 482us/step - acc: 0.9777 - loss: 0.0750

10427/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 482us/step - acc: 0.9778 - loss: 0.0749

10544/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 481us/step - acc: 0.9778 - loss: 0.0749

10641/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 482us/step - acc: 0.9778 - loss: 0.0748

10756/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 481us/step - acc: 0.9778 - loss: 0.0748

10877/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 481us/step - acc: 0.9778 - loss: 0.0747

10988/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 480us/step - acc: 0.9778 - loss: 0.0747

11103/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 480us/step - acc: 0.9778 - loss: 0.0746

11219/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 479us/step - acc: 0.9778 - loss: 0.0745

11337/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 479us/step - acc: 0.9778 - loss: 0.0745

11451/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 478us/step - acc: 0.9778 - loss: 0.0744

11536/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 479us/step - acc: 0.9778 - loss: 0.0744

11616/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 480us/step - acc: 0.9778 - loss: 0.0744

11722/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 480us/step - acc: 0.9778 - loss: 0.0743

11832/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 480us/step - acc: 0.9778 - loss: 0.0743

11945/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 480us/step - acc: 0.9778 - loss: 0.0742

12039/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 480us/step - acc: 0.9778 - loss: 0.0742

12135/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 480us/step - acc: 0.9778 - loss: 0.0741

12215/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 481us/step - acc: 0.9778 - loss: 0.0741

12308/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 482us/step - acc: 0.9778 - loss: 0.0741

12407/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 482us/step - acc: 0.9778 - loss: 0.0740

12523/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 482us/step - acc: 0.9778 - loss: 0.0740

12624/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 482us/step - acc: 0.9778 - loss: 0.0740

12724/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 482us/step - acc: 0.9778 - loss: 0.0739

12828/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 482us/step - acc: 0.9778 - loss: 0.0739

12943/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 481us/step - acc: 0.9778 - loss: 0.0739

13058/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 481us/step - acc: 0.9778 - loss: 0.0738

13169/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 481us/step - acc: 0.9778 - loss: 0.0738

13265/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 481us/step - acc: 0.9778 - loss: 0.0738

13325/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 483us/step - acc: 0.9778 - loss: 0.0737

13411/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 484us/step - acc: 0.9778 - loss: 0.0737

13517/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 483us/step - acc: 0.9778 - loss: 0.0737

13620/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 484us/step - acc: 0.9778 - loss: 0.0736

13685/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 485us/step - acc: 0.9778 - loss: 0.0736

13784/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 485us/step - acc: 0.9778 - loss: 0.0736

13881/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 485us/step - acc: 0.9778 - loss: 0.0736

13995/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 485us/step - acc: 0.9779 - loss: 0.0735

14107/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 485us/step - acc: 0.9779 - loss: 0.0735

14204/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 485us/step - acc: 0.9779 - loss: 0.0735

14319/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 484us/step - acc: 0.9779 - loss: 0.0734

14420/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 485us/step - acc: 0.9779 - loss: 0.0734

14551/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 484us/step - acc: 0.9779 - loss: 0.0733

14687/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 483us/step - acc: 0.9779 - loss: 0.0733

14820/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 482us/step - acc: 0.9779 - loss: 0.0733

14941/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 481us/step - acc: 0.9779 - loss: 0.0732

15051/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 481us/step - acc: 0.9779 - loss: 0.0732

15149/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 481us/step - acc: 0.9779 - loss: 0.0732

15270/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 481us/step - acc: 0.9779 - loss: 0.0732

15383/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 480us/step - acc: 0.9779 - loss: 0.0731

15495/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 480us/step - acc: 0.9779 - loss: 0.0731

15611/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 480us/step - acc: 0.9779 - loss: 0.0731

15730/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 479us/step - acc: 0.9779 - loss: 0.0731

15845/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 479us/step - acc: 0.9779 - loss: 0.0731

15965/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 479us/step - acc: 0.9779 - loss: 0.0730

16089/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 478us/step - acc: 0.9779 - loss: 0.0730

16210/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 478us/step - acc: 0.9779 - loss: 0.0730

16325/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 477us/step - acc: 0.9779 - loss: 0.0730

16423/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 477us/step - acc: 0.9779 - loss: 0.0730

16496/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 478us/step - acc: 0.9779 - loss: 0.0730

16578/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 479us/step - acc: 0.9779 - loss: 0.0730

16696/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 479us/step - acc: 0.9779 - loss: 0.0730

16815/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 478us/step - acc: 0.9779 - loss: 0.0730

16936/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 478us/step - acc: 0.9778 - loss: 0.0729

17044/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 478us/step - acc: 0.9778 - loss: 0.0729

17160/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 477us/step - acc: 0.9778 - loss: 0.0729

17281/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 477us/step - acc: 0.9778 - loss: 0.0729

17401/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 477us/step - acc: 0.9778 - loss: 0.0729

17518/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 476us/step - acc: 0.9778 - loss: 0.0729

17639/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 476us/step - acc: 0.9778 - loss: 0.0729

17763/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 475us/step - acc: 0.9778 - loss: 0.0729

17879/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 475us/step - acc: 0.9778 - loss: 0.0729

17996/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 475us/step - acc: 0.9778 - loss: 0.0729

18120/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 474us/step - acc: 0.9778 - loss: 0.0729

18244/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 474us/step - acc: 0.9778 - loss: 0.0729

18366/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 473us/step - acc: 0.9778 - loss: 0.0729

18498/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 473us/step - acc: 0.9778 - loss: 0.0728

18622/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 472us/step - acc: 0.9778 - loss: 0.0728

18748/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 472us/step - acc: 0.9778 - loss: 0.0728

18857/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 472us/step - acc: 0.9778 - loss: 0.0728

18979/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 471us/step - acc: 0.9778 - loss: 0.0728

19105/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 471us/step - acc: 0.9778 - loss: 0.0728

19231/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 470us/step - acc: 0.9778 - loss: 0.0728

19359/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 470us/step - acc: 0.9778 - loss: 0.0728

19491/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 469us/step - acc: 0.9778 - loss: 0.0728

19621/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 469us/step - acc: 0.9778 - loss: 0.0728

19750/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 468us/step - acc: 0.9778 - loss: 0.0728

19879/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 468us/step - acc: 0.9778 - loss: 0.0728

20006/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 467us/step - acc: 0.9778 - loss: 0.0728

20127/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 467us/step - acc: 0.9778 - loss: 0.0728

20260/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 466us/step - acc: 0.9778 - loss: 0.0727

20396/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 466us/step - acc: 0.9777 - loss: 0.0727

20529/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 465us/step - acc: 0.9777 - loss: 0.0727

20665/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 464us/step - acc: 0.9777 - loss: 0.0727

20796/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 464us/step - acc: 0.9777 - loss: 0.0727

20932/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 463us/step - acc: 0.9777 - loss: 0.0727

21067/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 463us/step - acc: 0.9777 - loss: 0.0727

21203/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 462us/step - acc: 0.9777 - loss: 0.0727

21342/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 461us/step - acc: 0.9777 - loss: 0.0727

21479/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 461us/step - acc: 0.9777 - loss: 0.0727

21612/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 460us/step - acc: 0.9777 - loss: 0.0727

21748/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 460us/step - acc: 0.9777 - loss: 0.0727

21882/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 459us/step - acc: 0.9777 - loss: 0.0727

22020/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 459us/step - acc: 0.9777 - loss: 0.0727

22151/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 458us/step - acc: 0.9777 - loss: 0.0727

22287/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 458us/step - acc: 0.9777 - loss: 0.0727

22426/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 457us/step - acc: 0.9777 - loss: 0.0727

22564/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 456us/step - acc: 0.9777 - loss: 0.0727

22699/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 456us/step - acc: 0.9777 - loss: 0.0727

22834/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 455us/step - acc: 0.9777 - loss: 0.0727

22971/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 455us/step - acc: 0.9777 - loss: 0.0727

23108/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 454us/step - acc: 0.9777 - loss: 0.0727

23246/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 454us/step - acc: 0.9777 - loss: 0.0727

23384/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 453us/step - acc: 0.9777 - loss: 0.0727

23518/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 453us/step - acc: 0.9776 - loss: 0.0727

23650/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 452us/step - acc: 0.9776 - loss: 0.0727

23785/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 452us/step - acc: 0.9776 - loss: 0.0727

23922/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 452us/step - acc: 0.9776 - loss: 0.0728

24059/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 451us/step - acc: 0.9776 - loss: 0.0728

24187/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 451us/step - acc: 0.9776 - loss: 0.0728

24316/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 450us/step - acc: 0.9776 - loss: 0.0728

24449/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 450us/step - acc: 0.9776 - loss: 0.0728

24583/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 450us/step - acc: 0.9776 - loss: 0.0728

24718/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 449us/step - acc: 0.9776 - loss: 0.0728

24850/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 449us/step - acc: 0.9776 - loss: 0.0728

24988/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 448us/step - acc: 0.9776 - loss: 0.0728

25122/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 448us/step - acc: 0.9776 - loss: 0.0728

25256/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 448us/step - acc: 0.9776 - loss: 0.0728

25393/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 447us/step - acc: 0.9776 - loss: 0.0728

25530/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 447us/step - acc: 0.9776 - loss: 0.0728

25667/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 446us/step - acc: 0.9776 - loss: 0.0728

25806/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 446us/step - acc: 0.9776 - loss: 0.0728

25945/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 445us/step - acc: 0.9776 - loss: 0.0728

26045/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 446us/step - acc: 0.9776 - loss: 0.0728

26166/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 445us/step - acc: 0.9776 - loss: 0.0728

26301/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 445us/step - acc: 0.9776 - loss: 0.0728

26438/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 445us/step - acc: 0.9776 - loss: 0.0728

26561/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 444us/step - acc: 0.9776 - loss: 0.0729

26697/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 444us/step - acc: 0.9775 - loss: 0.0729

26828/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 444us/step - acc: 0.9775 - loss: 0.0729

26951/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 444us/step - acc: 0.9775 - loss: 0.0729

27074/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 443us/step - acc: 0.9775 - loss: 0.0729

27202/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 443us/step - acc: 0.9775 - loss: 0.0729

27337/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 443us/step - acc: 0.9775 - loss: 0.0729

27471/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 443us/step - acc: 0.9775 - loss: 0.0729

27596/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 442us/step - acc: 0.9775 - loss: 0.0729

27671/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 443us/step - acc: 0.9775 - loss: 0.0729

27794/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 443us/step - acc: 0.9775 - loss: 0.0729

27924/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 443us/step - acc: 0.9775 - loss: 0.0729

27965/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 444us/step - acc: 0.9775 - loss: 0.0729

28017/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 445us/step - acc: 0.9775 - loss: 0.0729

28030/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 446us/step - acc: 0.9775 - loss: 0.0729

28059/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 448us/step - acc: 0.9775 - loss: 0.0729

28120/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 449us/step - acc: 0.9775 - loss: 0.0729

28197/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 449us/step - acc: 0.9775 - loss: 0.0729

28329/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 449us/step - acc: 0.9775 - loss: 0.0730

28460/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 448us/step - acc: 0.9775 - loss: 0.0730

28592/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 448us/step - acc: 0.9775 - loss: 0.0730

28720/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 448us/step - acc: 0.9775 - loss: 0.0730

28841/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 448us/step - acc: 0.9775 - loss: 0.0730

28963/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 448us/step - acc: 0.9775 - loss: 0.0730

29080/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 448us/step - acc: 0.9775 - loss: 0.0730

29204/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 447us/step - acc: 0.9775 - loss: 0.0730

29328/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 447us/step - acc: 0.9775 - loss: 0.0730

29452/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 447us/step - acc: 0.9775 - loss: 0.0730

29573/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 447us/step - acc: 0.9775 - loss: 0.0730

29693/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 447us/step - acc: 0.9775 - loss: 0.0730

29817/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 447us/step - acc: 0.9775 - loss: 0.0730

29946/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 446us/step - acc: 0.9775 - loss: 0.0730

30077/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 446us/step - acc: 0.9774 - loss: 0.0730

30202/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 446us/step - acc: 0.9774 - loss: 0.0730

30337/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 446us/step - acc: 0.9774 - loss: 0.0730

30463/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 445us/step - acc: 0.9774 - loss: 0.0730

30595/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 445us/step - acc: 0.9774 - loss: 0.0730

30725/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 445us/step - acc: 0.9774 - loss: 0.0730

30858/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 445us/step - acc: 0.9774 - loss: 0.0730

30986/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 444us/step - acc: 0.9774 - loss: 0.0730

31105/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 444us/step - acc: 0.9774 - loss: 0.0730

31220/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 444us/step - acc: 0.9774 - loss: 0.0730

31337/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 444us/step - acc: 0.9774 - loss: 0.0730

31461/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 444us/step - acc: 0.9774 - loss: 0.0730

31585/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 444us/step - acc: 0.9774 - loss: 0.0730

31714/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 444us/step - acc: 0.9774 - loss: 0.0730

31837/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 444us/step - acc: 0.9774 - loss: 0.0730

31969/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 443us/step - acc: 0.9774 - loss: 0.0730

32088/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 443us/step - acc: 0.9774 - loss: 0.0731

32214/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 443us/step - acc: 0.9774 - loss: 0.0731

32332/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 443us/step - acc: 0.9774 - loss: 0.0731

32452/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 443us/step - acc: 0.9774 - loss: 0.0731

32575/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 443us/step - acc: 0.9774 - loss: 0.0731

32701/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 443us/step - acc: 0.9774 - loss: 0.0731

32822/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 442us/step - acc: 0.9774 - loss: 0.0731

32949/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 442us/step - acc: 0.9774 - loss: 0.0731

33071/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 442us/step - acc: 0.9774 - loss: 0.0731

33200/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 442us/step - acc: 0.9774 - loss: 0.0731

33330/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 442us/step - acc: 0.9774 - loss: 0.0731

33429/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 442us/step - acc: 0.9774 - loss: 0.0731

33552/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 442us/step - acc: 0.9774 - loss: 0.0731

33663/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 442us/step - acc: 0.9774 - loss: 0.0731

33781/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 442us/step - acc: 0.9774 - loss: 0.0731

33903/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 442us/step - acc: 0.9774 - loss: 0.0731

34018/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 442us/step - acc: 0.9774 - loss: 0.0731

34146/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 441us/step - acc: 0.9774 - loss: 0.0731

34265/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 441us/step - acc: 0.9774 - loss: 0.0731

34392/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 441us/step - acc: 0.9773 - loss: 0.0731

34522/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 441us/step - acc: 0.9773 - loss: 0.0731

34654/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 441us/step - acc: 0.9773 - loss: 0.0731

34784/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 441us/step - acc: 0.9773 - loss: 0.0731

34914/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 440us/step - acc: 0.9773 - loss: 0.0731

35051/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 440us/step - acc: 0.9773 - loss: 0.0731

35190/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 440us/step - acc: 0.9773 - loss: 0.0731

35326/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 439us/step - acc: 0.9773 - loss: 0.0732

35464/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 439us/step - acc: 0.9773 - loss: 0.0732

35588/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 439us/step - acc: 0.9773 - loss: 0.0732

35717/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 439us/step - acc: 0.9773 - loss: 0.0732

35843/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 439us/step - acc: 0.9773 - loss: 0.0732

35969/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 439us/step - acc: 0.9773 - loss: 0.0732

36089/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 439us/step - acc: 0.9773 - loss: 0.0732

36203/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 439us/step - acc: 0.9773 - loss: 0.0732

36308/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 439us/step - acc: 0.9773 - loss: 0.0732

36425/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 439us/step - acc: 0.9773 - loss: 0.0732

36540/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 439us/step - acc: 0.9773 - loss: 0.0732

36665/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 438us/step - acc: 0.9773 - loss: 0.0732

36786/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 438us/step - acc: 0.9773 - loss: 0.0732

36908/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 438us/step - acc: 0.9773 - loss: 0.0732

37015/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 438us/step - acc: 0.9773 - loss: 0.0732

37148/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 438us/step - acc: 0.9773 - loss: 0.0732

37274/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 438us/step - acc: 0.9773 - loss: 0.0732 

37402/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 438us/step - acc: 0.9773 - loss: 0.0732

37522/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 438us/step - acc: 0.9773 - loss: 0.0732

37654/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 438us/step - acc: 0.9773 - loss: 0.0732

37792/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 437us/step - acc: 0.9773 - loss: 0.0732

37930/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 437us/step - acc: 0.9773 - loss: 0.0732

38063/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 437us/step - acc: 0.9773 - loss: 0.0732

38194/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 437us/step - acc: 0.9772 - loss: 0.0732

38319/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 437us/step - acc: 0.9772 - loss: 0.0733

38447/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 436us/step - acc: 0.9772 - loss: 0.0733

38578/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 436us/step - acc: 0.9772 - loss: 0.0733

38702/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 436us/step - acc: 0.9772 - loss: 0.0733

38828/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 436us/step - acc: 0.9772 - loss: 0.0733

38965/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 436us/step - acc: 0.9772 - loss: 0.0733

39097/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 436us/step - acc: 0.9772 - loss: 0.0733

39234/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 435us/step - acc: 0.9772 - loss: 0.0733

39369/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 435us/step - acc: 0.9772 - loss: 0.0733

39507/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 435us/step - acc: 0.9772 - loss: 0.0733

39644/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 435us/step - acc: 0.9772 - loss: 0.0733

39782/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 434us/step - acc: 0.9772 - loss: 0.0733

39920/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 434us/step - acc: 0.9772 - loss: 0.0734

40052/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 434us/step - acc: 0.9772 - loss: 0.0734

40174/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 434us/step - acc: 0.9772 - loss: 0.0734

40301/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 434us/step - acc: 0.9772 - loss: 0.0734

40429/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 434us/step - acc: 0.9772 - loss: 0.0734

40559/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 433us/step - acc: 0.9772 - loss: 0.0734

40686/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 433us/step - acc: 0.9772 - loss: 0.0734

40816/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 433us/step - acc: 0.9772 - loss: 0.0734

40951/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 433us/step - acc: 0.9772 - loss: 0.0734

41087/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 433us/step - acc: 0.9772 - loss: 0.0734

41226/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 433us/step - acc: 0.9772 - loss: 0.0734

41348/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 433us/step - acc: 0.9772 - loss: 0.0734

41481/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 432us/step - acc: 0.9772 - loss: 0.0735

41618/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 432us/step - acc: 0.9771 - loss: 0.0735

41754/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 432us/step - acc: 0.9771 - loss: 0.0735

41889/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 432us/step - acc: 0.9771 - loss: 0.0735

42021/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 432us/step - acc: 0.9771 - loss: 0.0735

42158/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 431us/step - acc: 0.9771 - loss: 0.0735

42291/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 431us/step - acc: 0.9771 - loss: 0.0735

42418/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 431us/step - acc: 0.9771 - loss: 0.0735

42552/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 431us/step - acc: 0.9771 - loss: 0.0735

42682/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 431us/step - acc: 0.9771 - loss: 0.0736

42814/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 431us/step - acc: 0.9771 - loss: 0.0736

42948/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 430us/step - acc: 0.9771 - loss: 0.0736

43080/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 430us/step - acc: 0.9771 - loss: 0.0736

43212/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 430us/step - acc: 0.9771 - loss: 0.0736

43337/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 430us/step - acc: 0.9771 - loss: 0.0736

43467/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 430us/step - acc: 0.9771 - loss: 0.0736

43597/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 430us/step - acc: 0.9771 - loss: 0.0736

43728/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 430us/step - acc: 0.9771 - loss: 0.0736

43853/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 430us/step - acc: 0.9771 - loss: 0.0737

43978/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 429us/step - acc: 0.9771 - loss: 0.0737

44098/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 429us/step - acc: 0.9771 - loss: 0.0737

44217/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 429us/step - acc: 0.9771 - loss: 0.0737

44342/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 429us/step - acc: 0.9771 - loss: 0.0737

44472/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 429us/step - acc: 0.9771 - loss: 0.0737

44608/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 429us/step - acc: 0.9771 - loss: 0.0737

44747/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 429us/step - acc: 0.9771 - loss: 0.0737

44880/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 429us/step - acc: 0.9771 - loss: 0.0737

45016/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 428us/step - acc: 0.9771 - loss: 0.0737

45146/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 428us/step - acc: 0.9770 - loss: 0.0737

45278/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 428us/step - acc: 0.9770 - loss: 0.0738

45415/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 428us/step - acc: 0.9770 - loss: 0.0738

45537/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 428us/step - acc: 0.9770 - loss: 0.0738

45662/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 428us/step - acc: 0.9770 - loss: 0.0738

45796/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 428us/step - acc: 0.9770 - loss: 0.0738

45927/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 428us/step - acc: 0.9770 - loss: 0.0738

46064/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 427us/step - acc: 0.9770 - loss: 0.0738

46202/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 427us/step - acc: 0.9770 - loss: 0.0738

46333/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 427us/step - acc: 0.9770 - loss: 0.0738

46469/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 427us/step - acc: 0.9770 - loss: 0.0739

46592/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 427us/step - acc: 0.9770 - loss: 0.0739

46726/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 427us/step - acc: 0.9770 - loss: 0.0739

46863/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 427us/step - acc: 0.9770 - loss: 0.0739

47001/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 426us/step - acc: 0.9770 - loss: 0.0739

47138/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 426us/step - acc: 0.9770 - loss: 0.0739

47267/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 426us/step - acc: 0.9770 - loss: 0.0739

47405/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 426us/step - acc: 0.9770 - loss: 0.0739

47543/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 426us/step - acc: 0.9770 - loss: 0.0739

47677/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 426us/step - acc: 0.9770 - loss: 0.0740

47782/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 426us/step - acc: 0.9770 - loss: 0.0740

47912/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 426us/step - acc: 0.9770 - loss: 0.0740

48047/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 425us/step - acc: 0.9770 - loss: 0.0740

48185/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 425us/step - acc: 0.9770 - loss: 0.0740

48320/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 425us/step - acc: 0.9769 - loss: 0.0740

48458/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 425us/step - acc: 0.9769 - loss: 0.0740

48591/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 425us/step - acc: 0.9769 - loss: 0.0740

48730/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 425us/step - acc: 0.9769 - loss: 0.0741

48864/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 425us/step - acc: 0.9769 - loss: 0.0741

48983/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 425us/step - acc: 0.9769 - loss: 0.0741

49111/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 424us/step - acc: 0.9769 - loss: 0.0741

49238/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 424us/step - acc: 0.9769 - loss: 0.0741

49374/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 424us/step - acc: 0.9769 - loss: 0.0741

49511/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 424us/step - acc: 0.9769 - loss: 0.0741

49651/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 424us/step - acc: 0.9769 - loss: 0.0741

49781/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 424us/step - acc: 0.9769 - loss: 0.0741

49916/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 424us/step - acc: 0.9769 - loss: 0.0742

50051/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 423us/step - acc: 0.9769 - loss: 0.0742

50181/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 423us/step - acc: 0.9769 - loss: 0.0742

50318/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 423us/step - acc: 0.9769 - loss: 0.0742

50454/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 423us/step - acc: 0.9769 - loss: 0.0742

50591/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 423us/step - acc: 0.9769 - loss: 0.0742

50716/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 423us/step - acc: 0.9769 - loss: 0.0742

50846/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 423us/step - acc: 0.9769 - loss: 0.0742

50984/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 423us/step - acc: 0.9769 - loss: 0.0742

51121/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 422us/step - acc: 0.9769 - loss: 0.0743

51254/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 422us/step - acc: 0.9769 - loss: 0.0743

51387/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 422us/step - acc: 0.9768 - loss: 0.0743

51523/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 422us/step - acc: 0.9768 - loss: 0.0743

51656/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 422us/step - acc: 0.9768 - loss: 0.0743

51777/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 422us/step - acc: 0.9768 - loss: 0.0743

51908/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 422us/step - acc: 0.9768 - loss: 0.0743

52037/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 422us/step - acc: 0.9768 - loss: 0.0743

52172/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 422us/step - acc: 0.9768 - loss: 0.0744

52305/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 422us/step - acc: 0.9768 - loss: 0.0744

52436/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 421us/step - acc: 0.9768 - loss: 0.0744

52560/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 421us/step - acc: 0.9768 - loss: 0.0744

52686/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 421us/step - acc: 0.9768 - loss: 0.0744

52816/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 421us/step - acc: 0.9768 - loss: 0.0744

52948/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 421us/step - acc: 0.9768 - loss: 0.0744

53074/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 421us/step - acc: 0.9768 - loss: 0.0744

53199/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 421us/step - acc: 0.9768 - loss: 0.0744

53334/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 421us/step - acc: 0.9768 - loss: 0.0745

53460/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 421us/step - acc: 0.9768 - loss: 0.0745

53591/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 421us/step - acc: 0.9768 - loss: 0.0745

53727/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 421us/step - acc: 0.9768 - loss: 0.0745

53863/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 421us/step - acc: 0.9768 - loss: 0.0745

54001/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 420us/step - acc: 0.9768 - loss: 0.0745

54138/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 420us/step - acc: 0.9768 - loss: 0.0745

54270/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 420us/step - acc: 0.9767 - loss: 0.0745

54407/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 420us/step - acc: 0.9767 - loss: 0.0745

54534/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 420us/step - acc: 0.9767 - loss: 0.0746

54656/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 420us/step - acc: 0.9767 - loss: 0.0746

54770/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 420us/step - acc: 0.9767 - loss: 0.0746

54891/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 420us/step - acc: 0.9767 - loss: 0.0746

55015/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 420us/step - acc: 0.9767 - loss: 0.0746

55141/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 420us/step - acc: 0.9767 - loss: 0.0746

55277/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 420us/step - acc: 0.9767 - loss: 0.0746

55415/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 420us/step - acc: 0.9767 - loss: 0.0746

55552/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 419us/step - acc: 0.9767 - loss: 0.0746

55689/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 419us/step - acc: 0.9767 - loss: 0.0746

55825/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 419us/step - acc: 0.9767 - loss: 0.0747

55963/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 419us/step - acc: 0.9767 - loss: 0.0747

56099/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 419us/step - acc: 0.9767 - loss: 0.0747

56237/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 419us/step - acc: 0.9767 - loss: 0.0747

56380/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 419us/step - acc: 0.9767 - loss: 0.0747

56510/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 419us/step - acc: 0.9767 - loss: 0.0747

56644/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 418us/step - acc: 0.9767 - loss: 0.0747

56778/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 418us/step - acc: 0.9767 - loss: 0.0747

56909/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 418us/step - acc: 0.9767 - loss: 0.0747

57045/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 418us/step - acc: 0.9767 - loss: 0.0747

57181/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 418us/step - acc: 0.9767 - loss: 0.0747

57318/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 418us/step - acc: 0.9767 - loss: 0.0748

57450/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 418us/step - acc: 0.9767 - loss: 0.0748

57579/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 418us/step - acc: 0.9767 - loss: 0.0748

57700/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 418us/step - acc: 0.9767 - loss: 0.0748

57730/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 418us/step - acc: 0.9767 - loss: 0.0748

57822/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 419us/step - acc: 0.9767 - loss: 0.0748

57945/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 419us/step - acc: 0.9767 - loss: 0.0748

58081/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 419us/step - acc: 0.9767 - loss: 0.0748

58203/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 419us/step - acc: 0.9766 - loss: 0.0748

58339/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 418us/step - acc: 0.9766 - loss: 0.0748

58476/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 418us/step - acc: 0.9766 - loss: 0.0748

58613/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 418us/step - acc: 0.9766 - loss: 0.0748

58751/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 418us/step - acc: 0.9766 - loss: 0.0748

58887/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 418us/step - acc: 0.9766 - loss: 0.0749

59022/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 418us/step - acc: 0.9766 - loss: 0.0749

59155/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 418us/step - acc: 0.9766 - loss: 0.0749

59288/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 418us/step - acc: 0.9766 - loss: 0.0749

59412/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 418us/step - acc: 0.9766 - loss: 0.0749

59548/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 417us/step - acc: 0.9766 - loss: 0.0749

59684/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 417us/step - acc: 0.9766 - loss: 0.0749

59821/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 417us/step - acc: 0.9766 - loss: 0.0749

59958/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 417us/step - acc: 0.9766 - loss: 0.0749

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 477us/step - acc: 0.9766 - loss: 0.0749 - val_acc: 0.9679 - val_loss: 0.1087

Epoch 6/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 12:38 13ms/step - acc: 1.0000 - loss: 6.6757e-06

  118/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 428us/step - acc: 0.9673 - loss: 0.0435     

  240/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 419us/step - acc: 0.9732 - loss: 0.0373

  350/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 431us/step - acc: 0.9756 - loss: 0.0353

  439/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 457us/step - acc: 0.9770 - loss: 0.0345

  547/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 459us/step - acc: 0.9777 - loss: 0.0362

  648/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 465us/step - acc: 0.9781 - loss: 0.0373

  771/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 456us/step - acc: 0.9781 - loss: 0.0395

  894/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 449us/step - acc: 0.9782 - loss: 0.0414

 1011/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 447us/step - acc: 0.9783 - loss: 0.0425

 1071/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 469us/step - acc: 0.9784 - loss: 0.0430

 1138/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 485us/step - acc: 0.9785 - loss: 0.0433

 1168/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 516us/step - acc: 0.9786 - loss: 0.0435

 1216/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 538us/step - acc: 0.9787 - loss: 0.0438

 1266/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 556us/step - acc: 0.9788 - loss: 0.0439

 1297/60000 ━━━━━━━━━━━━━━━━━━━━ 34s 581us/step - acc: 0.9788 - loss: 0.0440

 1363/60000 ━━━━━━━━━━━━━━━━━━━━ 34s 590us/step - acc: 0.9789 - loss: 0.0442

 1443/60000 ━━━━━━━━━━━━━━━━━━━━ 34s 592us/step - acc: 0.9791 - loss: 0.0443

 1496/60000 ━━━━━━━━━━━━━━━━━━━━ 35s 605us/step - acc: 0.9791 - loss: 0.0444

 1588/60000 ━━━━━━━━━━━━━━━━━━━━ 35s 601us/step - acc: 0.9793 - loss: 0.0445

 1649/60000 ━━━━━━━━━━━━━━━━━━━━ 35s 610us/step - acc: 0.9794 - loss: 0.0444

 1715/60000 ━━━━━━━━━━━━━━━━━━━━ 35s 615us/step - acc: 0.9795 - loss: 0.0444

 1810/60000 ━━━━━━━━━━━━━━━━━━━━ 35s 611us/step - acc: 0.9796 - loss: 0.0443

 1909/60000 ━━━━━━━━━━━━━━━━━━━━ 35s 605us/step - acc: 0.9798 - loss: 0.0443

 2010/60000 ━━━━━━━━━━━━━━━━━━━━ 34s 600us/step - acc: 0.9799 - loss: 0.0444

 2085/60000 ━━━━━━━━━━━━━━━━━━━━ 34s 602us/step - acc: 0.9799 - loss: 0.0445

 2159/60000 ━━━━━━━━━━━━━━━━━━━━ 34s 605us/step - acc: 0.9800 - loss: 0.0446

 2258/60000 ━━━━━━━━━━━━━━━━━━━━ 34s 601us/step - acc: 0.9801 - loss: 0.0446

 2342/60000 ━━━━━━━━━━━━━━━━━━━━ 34s 601us/step - acc: 0.9802 - loss: 0.0447

 2456/60000 ━━━━━━━━━━━━━━━━━━━━ 34s 593us/step - acc: 0.9803 - loss: 0.0447

 2572/60000 ━━━━━━━━━━━━━━━━━━━━ 33s 586us/step - acc: 0.9804 - loss: 0.0448

 2687/60000 ━━━━━━━━━━━━━━━━━━━━ 33s 579us/step - acc: 0.9805 - loss: 0.0451

 2809/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 572us/step - acc: 0.9805 - loss: 0.0453

 2876/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 576us/step - acc: 0.9805 - loss: 0.0455

 2989/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 571us/step - acc: 0.9805 - loss: 0.0458

 3102/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 567us/step - acc: 0.9805 - loss: 0.0461

 3219/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 562us/step - acc: 0.9805 - loss: 0.0465

 3337/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 557us/step - acc: 0.9806 - loss: 0.0468

 3459/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 552us/step - acc: 0.9805 - loss: 0.0472

 3574/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 548us/step - acc: 0.9805 - loss: 0.0476

 3693/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 544us/step - acc: 0.9805 - loss: 0.0479

 3811/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 540us/step - acc: 0.9805 - loss: 0.0481

 3925/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 537us/step - acc: 0.9806 - loss: 0.0484

 4053/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 533us/step - acc: 0.9806 - loss: 0.0486

 4178/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 529us/step - acc: 0.9806 - loss: 0.0488

 4311/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 524us/step - acc: 0.9807 - loss: 0.0490

 4445/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 520us/step - acc: 0.9807 - loss: 0.0492

 4579/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 515us/step - acc: 0.9807 - loss: 0.0494

 4707/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 512us/step - acc: 0.9807 - loss: 0.0496

 4819/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 511us/step - acc: 0.9807 - loss: 0.0497

 4932/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 509us/step - acc: 0.9807 - loss: 0.0499

 5052/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 507us/step - acc: 0.9807 - loss: 0.0500

 5163/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 506us/step - acc: 0.9808 - loss: 0.0501

 5270/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 505us/step - acc: 0.9808 - loss: 0.0502

 5389/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 503us/step - acc: 0.9808 - loss: 0.0503

 5499/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 502us/step - acc: 0.9808 - loss: 0.0504

 5620/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 500us/step - acc: 0.9808 - loss: 0.0505

 5736/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 499us/step - acc: 0.9809 - loss: 0.0506

 5854/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 498us/step - acc: 0.9809 - loss: 0.0507

 5968/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 496us/step - acc: 0.9809 - loss: 0.0507

 6072/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 496us/step - acc: 0.9809 - loss: 0.0508

 6184/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 495us/step - acc: 0.9809 - loss: 0.0508

 6304/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 494us/step - acc: 0.9810 - loss: 0.0509

 6424/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 493us/step - acc: 0.9810 - loss: 0.0509

 6539/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 492us/step - acc: 0.9810 - loss: 0.0510

 6646/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 491us/step - acc: 0.9810 - loss: 0.0510

 6764/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 490us/step - acc: 0.9810 - loss: 0.0511

 6886/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 489us/step - acc: 0.9810 - loss: 0.0511

 7005/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 488us/step - acc: 0.9811 - loss: 0.0512

 7127/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 486us/step - acc: 0.9811 - loss: 0.0512

 7250/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 485us/step - acc: 0.9811 - loss: 0.0512

 7371/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 484us/step - acc: 0.9811 - loss: 0.0513

 7420/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 487us/step - acc: 0.9811 - loss: 0.0513

 7468/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 491us/step - acc: 0.9811 - loss: 0.0513

 7556/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 492us/step - acc: 0.9811 - loss: 0.0513

 7653/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 492us/step - acc: 0.9811 - loss: 0.0514

 7752/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 492us/step - acc: 0.9811 - loss: 0.0514

 7863/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 492us/step - acc: 0.9811 - loss: 0.0515

 7981/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 491us/step - acc: 0.9811 - loss: 0.0515

 8096/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 490us/step - acc: 0.9811 - loss: 0.0515

 8212/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 489us/step - acc: 0.9811 - loss: 0.0516

 8322/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 489us/step - acc: 0.9811 - loss: 0.0516

 8438/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 488us/step - acc: 0.9811 - loss: 0.0517

 8554/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 487us/step - acc: 0.9811 - loss: 0.0517

 8670/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 487us/step - acc: 0.9811 - loss: 0.0518

 8772/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 487us/step - acc: 0.9811 - loss: 0.0518

 8884/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 486us/step - acc: 0.9812 - loss: 0.0518

 9005/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 485us/step - acc: 0.9812 - loss: 0.0519

 9125/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 484us/step - acc: 0.9812 - loss: 0.0519

 9245/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 483us/step - acc: 0.9812 - loss: 0.0520

 9354/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 483us/step - acc: 0.9812 - loss: 0.0520

 9468/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 483us/step - acc: 0.9812 - loss: 0.0520

 9591/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 482us/step - acc: 0.9812 - loss: 0.0521

 9708/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 481us/step - acc: 0.9812 - loss: 0.0521

 9836/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 480us/step - acc: 0.9812 - loss: 0.0521

 9948/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 480us/step - acc: 0.9813 - loss: 0.0522

10056/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 479us/step - acc: 0.9813 - loss: 0.0522

10180/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 478us/step - acc: 0.9813 - loss: 0.0522

10298/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 478us/step - acc: 0.9813 - loss: 0.0522

10415/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 477us/step - acc: 0.9813 - loss: 0.0523

10513/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 478us/step - acc: 0.9813 - loss: 0.0523

10623/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 477us/step - acc: 0.9813 - loss: 0.0523

10739/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 477us/step - acc: 0.9813 - loss: 0.0523

10857/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 476us/step - acc: 0.9813 - loss: 0.0524

10978/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 476us/step - acc: 0.9813 - loss: 0.0524

11090/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 475us/step - acc: 0.9814 - loss: 0.0524

11198/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 475us/step - acc: 0.9814 - loss: 0.0525

11323/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 475us/step - acc: 0.9814 - loss: 0.0525

11430/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 475us/step - acc: 0.9814 - loss: 0.0525

11537/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 474us/step - acc: 0.9814 - loss: 0.0525

11650/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 474us/step - acc: 0.9814 - loss: 0.0526

11764/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 474us/step - acc: 0.9814 - loss: 0.0526

11891/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 473us/step - acc: 0.9814 - loss: 0.0526

12022/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 472us/step - acc: 0.9814 - loss: 0.0527

12149/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 471us/step - acc: 0.9814 - loss: 0.0527

12283/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 470us/step - acc: 0.9814 - loss: 0.0528

12410/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 469us/step - acc: 0.9814 - loss: 0.0528

12530/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 469us/step - acc: 0.9814 - loss: 0.0528

12651/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 468us/step - acc: 0.9814 - loss: 0.0529

12780/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 468us/step - acc: 0.9814 - loss: 0.0529

12912/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 467us/step - acc: 0.9814 - loss: 0.0530

13047/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 466us/step - acc: 0.9814 - loss: 0.0530

13167/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 465us/step - acc: 0.9814 - loss: 0.0530

13301/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 464us/step - acc: 0.9814 - loss: 0.0531

13412/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 464us/step - acc: 0.9814 - loss: 0.0531

13519/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 464us/step - acc: 0.9814 - loss: 0.0532

13631/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 464us/step - acc: 0.9814 - loss: 0.0532

13749/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 464us/step - acc: 0.9814 - loss: 0.0533

13847/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 464us/step - acc: 0.9814 - loss: 0.0533

13960/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 464us/step - acc: 0.9814 - loss: 0.0533

14081/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 464us/step - acc: 0.9814 - loss: 0.0534

14196/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 464us/step - acc: 0.9814 - loss: 0.0534

14300/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 464us/step - acc: 0.9814 - loss: 0.0534

14404/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 464us/step - acc: 0.9814 - loss: 0.0535

14499/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 464us/step - acc: 0.9814 - loss: 0.0535

14616/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 464us/step - acc: 0.9814 - loss: 0.0536

14733/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 464us/step - acc: 0.9813 - loss: 0.0536

14851/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 463us/step - acc: 0.9813 - loss: 0.0536

14967/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 463us/step - acc: 0.9813 - loss: 0.0537

15027/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 465us/step - acc: 0.9813 - loss: 0.0537

15091/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 466us/step - acc: 0.9813 - loss: 0.0537

15192/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 466us/step - acc: 0.9813 - loss: 0.0537

15304/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 466us/step - acc: 0.9813 - loss: 0.0538

15414/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 466us/step - acc: 0.9813 - loss: 0.0538

15520/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 466us/step - acc: 0.9813 - loss: 0.0538

15627/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 466us/step - acc: 0.9813 - loss: 0.0539

15734/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 466us/step - acc: 0.9813 - loss: 0.0539

15846/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 466us/step - acc: 0.9813 - loss: 0.0539

15966/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 466us/step - acc: 0.9813 - loss: 0.0539

16083/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 466us/step - acc: 0.9813 - loss: 0.0540

16201/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 465us/step - acc: 0.9813 - loss: 0.0540

16310/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 465us/step - acc: 0.9813 - loss: 0.0540

16414/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 465us/step - acc: 0.9813 - loss: 0.0540

16524/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 465us/step - acc: 0.9813 - loss: 0.0540

16631/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 465us/step - acc: 0.9813 - loss: 0.0541

16750/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 465us/step - acc: 0.9813 - loss: 0.0541

16868/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 465us/step - acc: 0.9813 - loss: 0.0541

16978/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 465us/step - acc: 0.9813 - loss: 0.0541

17095/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 464us/step - acc: 0.9813 - loss: 0.0541

17214/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 464us/step - acc: 0.9813 - loss: 0.0541

17337/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 464us/step - acc: 0.9813 - loss: 0.0542

17455/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 463us/step - acc: 0.9813 - loss: 0.0542

17573/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 463us/step - acc: 0.9813 - loss: 0.0542

17693/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 463us/step - acc: 0.9813 - loss: 0.0542

17814/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 463us/step - acc: 0.9813 - loss: 0.0542

17919/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 463us/step - acc: 0.9814 - loss: 0.0543

18049/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 462us/step - acc: 0.9814 - loss: 0.0543

18177/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 462us/step - acc: 0.9814 - loss: 0.0543

18306/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 461us/step - acc: 0.9814 - loss: 0.0543

18435/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 461us/step - acc: 0.9814 - loss: 0.0543

18565/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 460us/step - acc: 0.9814 - loss: 0.0543

18691/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 460us/step - acc: 0.9814 - loss: 0.0543

18814/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 459us/step - acc: 0.9814 - loss: 0.0544

18936/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 459us/step - acc: 0.9814 - loss: 0.0544

19051/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 459us/step - acc: 0.9813 - loss: 0.0544

19172/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 459us/step - acc: 0.9813 - loss: 0.0544

19280/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 459us/step - acc: 0.9813 - loss: 0.0544

19404/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 458us/step - acc: 0.9813 - loss: 0.0545

19532/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 458us/step - acc: 0.9813 - loss: 0.0545

19660/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 457us/step - acc: 0.9813 - loss: 0.0545

19783/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 457us/step - acc: 0.9813 - loss: 0.0545

19902/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 457us/step - acc: 0.9813 - loss: 0.0545

20027/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 457us/step - acc: 0.9813 - loss: 0.0546

20140/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 456us/step - acc: 0.9813 - loss: 0.0546

20224/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 457us/step - acc: 0.9813 - loss: 0.0546

20267/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 459us/step - acc: 0.9813 - loss: 0.0546

20355/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 459us/step - acc: 0.9813 - loss: 0.0546

20458/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 459us/step - acc: 0.9813 - loss: 0.0546

20588/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 459us/step - acc: 0.9813 - loss: 0.0547

20673/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 459us/step - acc: 0.9813 - loss: 0.0547

20725/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 461us/step - acc: 0.9813 - loss: 0.0547

20851/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 460us/step - acc: 0.9813 - loss: 0.0547

20980/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 460us/step - acc: 0.9813 - loss: 0.0547

21112/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 459us/step - acc: 0.9813 - loss: 0.0548

21247/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 459us/step - acc: 0.9813 - loss: 0.0548

21380/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 458us/step - acc: 0.9813 - loss: 0.0548

21502/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 458us/step - acc: 0.9813 - loss: 0.0548

21636/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 457us/step - acc: 0.9813 - loss: 0.0549

21769/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 457us/step - acc: 0.9813 - loss: 0.0549

21890/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 457us/step - acc: 0.9813 - loss: 0.0549

21998/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 457us/step - acc: 0.9812 - loss: 0.0549

22131/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 456us/step - acc: 0.9812 - loss: 0.0549

22263/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 456us/step - acc: 0.9812 - loss: 0.0550

22394/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 455us/step - acc: 0.9812 - loss: 0.0550

22530/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 455us/step - acc: 0.9812 - loss: 0.0550

22662/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 454us/step - acc: 0.9812 - loss: 0.0551

22796/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 454us/step - acc: 0.9812 - loss: 0.0551

22934/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 453us/step - acc: 0.9812 - loss: 0.0551

23069/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 453us/step - acc: 0.9812 - loss: 0.0551

23198/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 453us/step - acc: 0.9812 - loss: 0.0552

23330/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 452us/step - acc: 0.9812 - loss: 0.0552

23466/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 452us/step - acc: 0.9812 - loss: 0.0552

23600/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 451us/step - acc: 0.9812 - loss: 0.0552

23730/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 451us/step - acc: 0.9812 - loss: 0.0553

23865/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 450us/step - acc: 0.9812 - loss: 0.0553

24002/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 450us/step - acc: 0.9812 - loss: 0.0553

24133/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 450us/step - acc: 0.9812 - loss: 0.0554

24269/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 449us/step - acc: 0.9812 - loss: 0.0554

24406/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 449us/step - acc: 0.9812 - loss: 0.0554

24541/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 448us/step - acc: 0.9811 - loss: 0.0555

24674/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 448us/step - acc: 0.9811 - loss: 0.0555

24809/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 447us/step - acc: 0.9811 - loss: 0.0555

24936/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 447us/step - acc: 0.9811 - loss: 0.0555

25056/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 447us/step - acc: 0.9811 - loss: 0.0556

25176/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 447us/step - acc: 0.9811 - loss: 0.0556

25292/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 447us/step - acc: 0.9811 - loss: 0.0556

25416/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 447us/step - acc: 0.9811 - loss: 0.0557

25535/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 447us/step - acc: 0.9811 - loss: 0.0557

25668/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 446us/step - acc: 0.9811 - loss: 0.0557

25789/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 446us/step - acc: 0.9811 - loss: 0.0557

25905/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 446us/step - acc: 0.9811 - loss: 0.0557

26025/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 446us/step - acc: 0.9811 - loss: 0.0558

26146/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 446us/step - acc: 0.9811 - loss: 0.0558

26276/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 445us/step - acc: 0.9811 - loss: 0.0558

26405/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 445us/step - acc: 0.9811 - loss: 0.0558

26538/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 445us/step - acc: 0.9810 - loss: 0.0559

26671/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 444us/step - acc: 0.9810 - loss: 0.0559

26805/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 444us/step - acc: 0.9810 - loss: 0.0559

26940/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 444us/step - acc: 0.9810 - loss: 0.0560

27071/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 443us/step - acc: 0.9810 - loss: 0.0560

27205/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 443us/step - acc: 0.9810 - loss: 0.0560

27334/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 443us/step - acc: 0.9810 - loss: 0.0560

27470/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 443us/step - acc: 0.9810 - loss: 0.0561

27607/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 442us/step - acc: 0.9810 - loss: 0.0561

27739/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 442us/step - acc: 0.9810 - loss: 0.0561

27871/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 442us/step - acc: 0.9810 - loss: 0.0562

27983/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 442us/step - acc: 0.9810 - loss: 0.0562

28084/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 442us/step - acc: 0.9810 - loss: 0.0562

28208/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 442us/step - acc: 0.9810 - loss: 0.0562

28341/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 441us/step - acc: 0.9810 - loss: 0.0562

28475/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 441us/step - acc: 0.9809 - loss: 0.0563

28606/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 441us/step - acc: 0.9809 - loss: 0.0563

28735/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 441us/step - acc: 0.9809 - loss: 0.0563

28848/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 441us/step - acc: 0.9809 - loss: 0.0564

28963/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 441us/step - acc: 0.9809 - loss: 0.0564

29077/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 441us/step - acc: 0.9809 - loss: 0.0564

29199/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 440us/step - acc: 0.9809 - loss: 0.0564

29330/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 440us/step - acc: 0.9809 - loss: 0.0564

29458/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 440us/step - acc: 0.9809 - loss: 0.0565

29587/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 440us/step - acc: 0.9809 - loss: 0.0565

29718/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 439us/step - acc: 0.9809 - loss: 0.0565

29847/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 439us/step - acc: 0.9809 - loss: 0.0566

29977/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 439us/step - acc: 0.9809 - loss: 0.0566

30111/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 439us/step - acc: 0.9809 - loss: 0.0566

30179/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 440us/step - acc: 0.9809 - loss: 0.0566

30247/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 440us/step - acc: 0.9809 - loss: 0.0566

30334/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 441us/step - acc: 0.9809 - loss: 0.0567

30425/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 441us/step - acc: 0.9808 - loss: 0.0567

30522/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 441us/step - acc: 0.9808 - loss: 0.0567

30632/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 441us/step - acc: 0.9808 - loss: 0.0567

30740/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 441us/step - acc: 0.9808 - loss: 0.0567

30834/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 442us/step - acc: 0.9808 - loss: 0.0568

30913/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 442us/step - acc: 0.9808 - loss: 0.0568

31025/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 442us/step - acc: 0.9808 - loss: 0.0568

31138/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 442us/step - acc: 0.9808 - loss: 0.0568

31257/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 442us/step - acc: 0.9808 - loss: 0.0568

31384/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 442us/step - acc: 0.9808 - loss: 0.0569

31508/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 442us/step - acc: 0.9808 - loss: 0.0569

31633/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 442us/step - acc: 0.9808 - loss: 0.0569

31760/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 441us/step - acc: 0.9808 - loss: 0.0569

31895/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 441us/step - acc: 0.9808 - loss: 0.0570

32009/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 441us/step - acc: 0.9808 - loss: 0.0570

32133/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 441us/step - acc: 0.9808 - loss: 0.0570

32264/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 441us/step - acc: 0.9808 - loss: 0.0570

32376/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 441us/step - acc: 0.9808 - loss: 0.0571

32508/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 441us/step - acc: 0.9808 - loss: 0.0571

32643/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 440us/step - acc: 0.9808 - loss: 0.0571

32779/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 440us/step - acc: 0.9807 - loss: 0.0571

32914/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 440us/step - acc: 0.9807 - loss: 0.0572

33043/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 439us/step - acc: 0.9807 - loss: 0.0572

33177/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 439us/step - acc: 0.9807 - loss: 0.0572

33311/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 439us/step - acc: 0.9807 - loss: 0.0572

33445/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 439us/step - acc: 0.9807 - loss: 0.0573

33581/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 438us/step - acc: 0.9807 - loss: 0.0573

33719/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 438us/step - acc: 0.9807 - loss: 0.0573

33854/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 438us/step - acc: 0.9807 - loss: 0.0573

33990/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 438us/step - acc: 0.9807 - loss: 0.0574

34127/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 437us/step - acc: 0.9807 - loss: 0.0574

34265/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 437us/step - acc: 0.9807 - loss: 0.0574

34403/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 437us/step - acc: 0.9807 - loss: 0.0574

34538/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 436us/step - acc: 0.9807 - loss: 0.0575

34674/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 436us/step - acc: 0.9807 - loss: 0.0575

34805/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 436us/step - acc: 0.9807 - loss: 0.0575

34940/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 436us/step - acc: 0.9806 - loss: 0.0576

35066/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 436us/step - acc: 0.9806 - loss: 0.0576

35198/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 435us/step - acc: 0.9806 - loss: 0.0576

35327/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 435us/step - acc: 0.9806 - loss: 0.0576

35463/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 435us/step - acc: 0.9806 - loss: 0.0577

35599/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 435us/step - acc: 0.9806 - loss: 0.0577

35731/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9806 - loss: 0.0577

35865/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9806 - loss: 0.0577

36001/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9806 - loss: 0.0578

36136/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9806 - loss: 0.0578

36272/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9806 - loss: 0.0578

36409/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 433us/step - acc: 0.9806 - loss: 0.0579

36543/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 433us/step - acc: 0.9806 - loss: 0.0579

36679/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 433us/step - acc: 0.9806 - loss: 0.0579

36813/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 433us/step - acc: 0.9806 - loss: 0.0580

36948/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 432us/step - acc: 0.9805 - loss: 0.0580 

37080/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 432us/step - acc: 0.9805 - loss: 0.0580

37214/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 432us/step - acc: 0.9805 - loss: 0.0580

37347/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 432us/step - acc: 0.9805 - loss: 0.0581

37481/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 432us/step - acc: 0.9805 - loss: 0.0581

37618/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 431us/step - acc: 0.9805 - loss: 0.0581

37741/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 431us/step - acc: 0.9805 - loss: 0.0582

37877/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 431us/step - acc: 0.9805 - loss: 0.0582

38011/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 431us/step - acc: 0.9805 - loss: 0.0582

38142/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 431us/step - acc: 0.9805 - loss: 0.0582

38275/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 431us/step - acc: 0.9805 - loss: 0.0583

38402/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 430us/step - acc: 0.9805 - loss: 0.0583

38539/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 430us/step - acc: 0.9805 - loss: 0.0583

38675/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 430us/step - acc: 0.9804 - loss: 0.0584

38808/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 430us/step - acc: 0.9804 - loss: 0.0584

38941/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 430us/step - acc: 0.9804 - loss: 0.0584

39076/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 429us/step - acc: 0.9804 - loss: 0.0584

39179/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 430us/step - acc: 0.9804 - loss: 0.0585

39288/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 430us/step - acc: 0.9804 - loss: 0.0585

39405/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 430us/step - acc: 0.9804 - loss: 0.0585

39534/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 429us/step - acc: 0.9804 - loss: 0.0585

39667/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 429us/step - acc: 0.9804 - loss: 0.0586

39803/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 429us/step - acc: 0.9804 - loss: 0.0586

39937/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 429us/step - acc: 0.9804 - loss: 0.0586

40073/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 429us/step - acc: 0.9804 - loss: 0.0587

40209/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 429us/step - acc: 0.9804 - loss: 0.0587

40342/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 428us/step - acc: 0.9804 - loss: 0.0587

40470/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 428us/step - acc: 0.9803 - loss: 0.0587

40601/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 428us/step - acc: 0.9803 - loss: 0.0588

40723/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 428us/step - acc: 0.9803 - loss: 0.0588

40844/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 428us/step - acc: 0.9803 - loss: 0.0588

40970/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 428us/step - acc: 0.9803 - loss: 0.0588

41102/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 428us/step - acc: 0.9803 - loss: 0.0589

41231/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 428us/step - acc: 0.9803 - loss: 0.0589

41364/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 427us/step - acc: 0.9803 - loss: 0.0589

41498/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 427us/step - acc: 0.9803 - loss: 0.0589

41634/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 427us/step - acc: 0.9803 - loss: 0.0590

41769/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 427us/step - acc: 0.9803 - loss: 0.0590

41902/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 427us/step - acc: 0.9803 - loss: 0.0590

42038/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 427us/step - acc: 0.9803 - loss: 0.0590

42177/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 426us/step - acc: 0.9803 - loss: 0.0591

42308/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 426us/step - acc: 0.9803 - loss: 0.0591

42442/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 426us/step - acc: 0.9802 - loss: 0.0591

42578/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 426us/step - acc: 0.9802 - loss: 0.0591

42716/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 426us/step - acc: 0.9802 - loss: 0.0592

42851/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 426us/step - acc: 0.9802 - loss: 0.0592

42980/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 425us/step - acc: 0.9802 - loss: 0.0592

43116/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 425us/step - acc: 0.9802 - loss: 0.0593

43252/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 425us/step - acc: 0.9802 - loss: 0.0593

43387/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 425us/step - acc: 0.9802 - loss: 0.0593

43524/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 425us/step - acc: 0.9802 - loss: 0.0593

43660/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 425us/step - acc: 0.9802 - loss: 0.0594

43791/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 424us/step - acc: 0.9802 - loss: 0.0594

43921/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 424us/step - acc: 0.9802 - loss: 0.0594

44057/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 424us/step - acc: 0.9802 - loss: 0.0594

44192/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 424us/step - acc: 0.9802 - loss: 0.0594

44326/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 424us/step - acc: 0.9801 - loss: 0.0595

44461/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 424us/step - acc: 0.9801 - loss: 0.0595

44598/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 424us/step - acc: 0.9801 - loss: 0.0595

44733/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 423us/step - acc: 0.9801 - loss: 0.0595

44867/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 423us/step - acc: 0.9801 - loss: 0.0596

44985/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 423us/step - acc: 0.9801 - loss: 0.0596

45104/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 423us/step - acc: 0.9801 - loss: 0.0596

45238/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 423us/step - acc: 0.9801 - loss: 0.0596

45356/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 423us/step - acc: 0.9801 - loss: 0.0596

45462/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 423us/step - acc: 0.9801 - loss: 0.0597

45572/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 423us/step - acc: 0.9801 - loss: 0.0597

45692/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 423us/step - acc: 0.9801 - loss: 0.0597

45818/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 423us/step - acc: 0.9801 - loss: 0.0597

45945/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 423us/step - acc: 0.9801 - loss: 0.0597

46076/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 423us/step - acc: 0.9801 - loss: 0.0598

46204/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 423us/step - acc: 0.9801 - loss: 0.0598

46337/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 423us/step - acc: 0.9801 - loss: 0.0598

46471/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 423us/step - acc: 0.9800 - loss: 0.0598

46603/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 423us/step - acc: 0.9800 - loss: 0.0599

46737/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 422us/step - acc: 0.9800 - loss: 0.0599

46873/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 422us/step - acc: 0.9800 - loss: 0.0599

47010/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 422us/step - acc: 0.9800 - loss: 0.0599

47145/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 422us/step - acc: 0.9800 - loss: 0.0599

47279/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 422us/step - acc: 0.9800 - loss: 0.0600

47411/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 422us/step - acc: 0.9800 - loss: 0.0600

47541/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 422us/step - acc: 0.9800 - loss: 0.0600

47666/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 422us/step - acc: 0.9800 - loss: 0.0600

47795/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 421us/step - acc: 0.9800 - loss: 0.0600

47929/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 421us/step - acc: 0.9800 - loss: 0.0601

48062/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 421us/step - acc: 0.9800 - loss: 0.0601

48183/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 421us/step - acc: 0.9800 - loss: 0.0601

48318/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 421us/step - acc: 0.9800 - loss: 0.0601

48450/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 421us/step - acc: 0.9800 - loss: 0.0601

48586/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 421us/step - acc: 0.9800 - loss: 0.0602

48716/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 421us/step - acc: 0.9799 - loss: 0.0602

48835/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 421us/step - acc: 0.9799 - loss: 0.0602

48954/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 421us/step - acc: 0.9799 - loss: 0.0602

49072/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 421us/step - acc: 0.9799 - loss: 0.0602

49194/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 421us/step - acc: 0.9799 - loss: 0.0603

49317/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 421us/step - acc: 0.9799 - loss: 0.0603

49445/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 421us/step - acc: 0.9799 - loss: 0.0603

49580/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 420us/step - acc: 0.9799 - loss: 0.0603

49715/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 420us/step - acc: 0.9799 - loss: 0.0604

49847/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 420us/step - acc: 0.9799 - loss: 0.0604

49979/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 420us/step - acc: 0.9799 - loss: 0.0604

50109/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 420us/step - acc: 0.9799 - loss: 0.0604

50239/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 420us/step - acc: 0.9799 - loss: 0.0604

50374/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 420us/step - acc: 0.9799 - loss: 0.0605

50510/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 420us/step - acc: 0.9799 - loss: 0.0605

50639/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 420us/step - acc: 0.9799 - loss: 0.0605

50766/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9799 - loss: 0.0605

50895/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9799 - loss: 0.0606

51029/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9798 - loss: 0.0606

51155/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9798 - loss: 0.0606

51271/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9798 - loss: 0.0606

51395/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9798 - loss: 0.0606

51522/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9798 - loss: 0.0607

51651/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9798 - loss: 0.0607

51774/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9798 - loss: 0.0607

51896/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9798 - loss: 0.0607

52019/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9798 - loss: 0.0607

52152/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9798 - loss: 0.0608

52281/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9798 - loss: 0.0608

52415/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9798 - loss: 0.0608

52546/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9798 - loss: 0.0608

52682/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9798 - loss: 0.0609

52811/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 418us/step - acc: 0.9798 - loss: 0.0609

52945/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 418us/step - acc: 0.9798 - loss: 0.0609

53081/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 418us/step - acc: 0.9798 - loss: 0.0609

53205/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 418us/step - acc: 0.9797 - loss: 0.0609

53322/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 418us/step - acc: 0.9797 - loss: 0.0610

53451/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 418us/step - acc: 0.9797 - loss: 0.0610

53573/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 418us/step - acc: 0.9797 - loss: 0.0610

53692/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 418us/step - acc: 0.9797 - loss: 0.0610

53804/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 418us/step - acc: 0.9797 - loss: 0.0610

53933/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 418us/step - acc: 0.9797 - loss: 0.0611

54064/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 418us/step - acc: 0.9797 - loss: 0.0611

54194/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 418us/step - acc: 0.9797 - loss: 0.0611

54326/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 418us/step - acc: 0.9797 - loss: 0.0611

54459/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 418us/step - acc: 0.9797 - loss: 0.0611

54595/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 418us/step - acc: 0.9797 - loss: 0.0612

54731/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 418us/step - acc: 0.9797 - loss: 0.0612

54864/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 417us/step - acc: 0.9797 - loss: 0.0612

54992/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 417us/step - acc: 0.9797 - loss: 0.0612

55124/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 417us/step - acc: 0.9797 - loss: 0.0612

55260/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 417us/step - acc: 0.9797 - loss: 0.0613

55396/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 417us/step - acc: 0.9797 - loss: 0.0613

55527/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 417us/step - acc: 0.9797 - loss: 0.0613

55660/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 417us/step - acc: 0.9796 - loss: 0.0613

55795/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 417us/step - acc: 0.9796 - loss: 0.0613

55932/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 417us/step - acc: 0.9796 - loss: 0.0614

56069/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 417us/step - acc: 0.9796 - loss: 0.0614

56204/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 416us/step - acc: 0.9796 - loss: 0.0614

56338/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 416us/step - acc: 0.9796 - loss: 0.0614

56471/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 416us/step - acc: 0.9796 - loss: 0.0614

56604/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 416us/step - acc: 0.9796 - loss: 0.0615

56739/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 416us/step - acc: 0.9796 - loss: 0.0615

56875/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 416us/step - acc: 0.9796 - loss: 0.0615

57011/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 416us/step - acc: 0.9796 - loss: 0.0615

57145/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 416us/step - acc: 0.9796 - loss: 0.0615

57280/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 416us/step - acc: 0.9796 - loss: 0.0616

57416/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 416us/step - acc: 0.9796 - loss: 0.0616

57553/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 415us/step - acc: 0.9796 - loss: 0.0616

57687/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 415us/step - acc: 0.9796 - loss: 0.0616

57822/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 415us/step - acc: 0.9796 - loss: 0.0617

57957/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 415us/step - acc: 0.9796 - loss: 0.0617

58093/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 415us/step - acc: 0.9796 - loss: 0.0617

58228/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 415us/step - acc: 0.9795 - loss: 0.0617

58362/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 415us/step - acc: 0.9795 - loss: 0.0617

58499/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 415us/step - acc: 0.9795 - loss: 0.0618

58630/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 415us/step - acc: 0.9795 - loss: 0.0618

58763/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 415us/step - acc: 0.9795 - loss: 0.0618

58898/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 414us/step - acc: 0.9795 - loss: 0.0618

59035/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 414us/step - acc: 0.9795 - loss: 0.0618

59168/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 414us/step - acc: 0.9795 - loss: 0.0619

59295/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 414us/step - acc: 0.9795 - loss: 0.0619

59426/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 414us/step - acc: 0.9795 - loss: 0.0619

59557/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 414us/step - acc: 0.9795 - loss: 0.0619

59690/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 414us/step - acc: 0.9795 - loss: 0.0619

59825/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 414us/step - acc: 0.9795 - loss: 0.0620

59958/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 414us/step - acc: 0.9795 - loss: 0.0620

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 474us/step - acc: 0.9795 - loss: 0.0620 - val_acc: 0.9648 - val_loss: 0.1224

Epoch 7/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 9:03 9ms/step - acc: 1.0000 - loss: 7.7483e-05

  133/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 381us/step - acc: 0.9889 - loss: 0.0230   

  266/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 379us/step - acc: 0.9914 - loss: 0.0220

  404/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 374us/step - acc: 0.9906 - loss: 0.0248

  541/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 372us/step - acc: 0.9902 - loss: 0.0254

  679/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 370us/step - acc: 0.9898 - loss: 0.0259

  817/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 369us/step - acc: 0.9892 - loss: 0.0279

  952/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 369us/step - acc: 0.9886 - loss: 0.0296

 1090/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 368us/step - acc: 0.9880 - loss: 0.0311

 1229/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 368us/step - acc: 0.9874 - loss: 0.0326

 1366/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 368us/step - acc: 0.9869 - loss: 0.0337

 1500/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 368us/step - acc: 0.9867 - loss: 0.0346

 1637/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 368us/step - acc: 0.9865 - loss: 0.0352

 1773/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 368us/step - acc: 0.9865 - loss: 0.0355

 1909/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 368us/step - acc: 0.9864 - loss: 0.0359

 2046/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 368us/step - acc: 0.9864 - loss: 0.0362

 2186/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 368us/step - acc: 0.9864 - loss: 0.0364

 2321/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 368us/step - acc: 0.9864 - loss: 0.0365

 2459/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 368us/step - acc: 0.9864 - loss: 0.0367

 2596/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 368us/step - acc: 0.9864 - loss: 0.0368

 2731/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 368us/step - acc: 0.9864 - loss: 0.0369

 2869/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 368us/step - acc: 0.9865 - loss: 0.0369

 3009/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 367us/step - acc: 0.9865 - loss: 0.0369

 3140/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 368us/step - acc: 0.9865 - loss: 0.0370

 3264/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 369us/step - acc: 0.9865 - loss: 0.0370

 3388/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 371us/step - acc: 0.9865 - loss: 0.0371

 3514/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9865 - loss: 0.0372

 3648/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9865 - loss: 0.0373

 3784/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9865 - loss: 0.0374

 3920/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9865 - loss: 0.0375

 4054/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9865 - loss: 0.0376

 4188/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9865 - loss: 0.0377

 4324/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9864 - loss: 0.0379

 4457/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9864 - loss: 0.0381

 4594/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9863 - loss: 0.0384

 4735/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 371us/step - acc: 0.9863 - loss: 0.0386

 4876/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 371us/step - acc: 0.9862 - loss: 0.0387

 5012/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 371us/step - acc: 0.9862 - loss: 0.0389

 5150/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 371us/step - acc: 0.9861 - loss: 0.0391

 5283/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 371us/step - acc: 0.9861 - loss: 0.0393

 5420/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 371us/step - acc: 0.9860 - loss: 0.0394

 5555/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 371us/step - acc: 0.9860 - loss: 0.0396

 5691/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 371us/step - acc: 0.9860 - loss: 0.0398

 5787/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 373us/step - acc: 0.9859 - loss: 0.0399

 5922/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 373us/step - acc: 0.9859 - loss: 0.0401

 6049/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 373us/step - acc: 0.9858 - loss: 0.0403

 6170/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9858 - loss: 0.0404

 6278/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 376us/step - acc: 0.9857 - loss: 0.0406

 6358/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 379us/step - acc: 0.9857 - loss: 0.0406

 6424/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 383us/step - acc: 0.9857 - loss: 0.0407

 6508/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 386us/step - acc: 0.9857 - loss: 0.0408

 6619/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 387us/step - acc: 0.9856 - loss: 0.0409

 6737/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 388us/step - acc: 0.9856 - loss: 0.0410

 6854/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 388us/step - acc: 0.9856 - loss: 0.0412

 6941/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 391us/step - acc: 0.9855 - loss: 0.0413

 7055/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 391us/step - acc: 0.9855 - loss: 0.0414

 7172/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 392us/step - acc: 0.9854 - loss: 0.0415

 7293/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 392us/step - acc: 0.9854 - loss: 0.0416

 7411/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 393us/step - acc: 0.9854 - loss: 0.0418

 7532/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 393us/step - acc: 0.9853 - loss: 0.0419

 7610/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 396us/step - acc: 0.9853 - loss: 0.0419

 7667/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 399us/step - acc: 0.9853 - loss: 0.0420

 7722/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 403us/step - acc: 0.9853 - loss: 0.0421

 7777/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 407us/step - acc: 0.9853 - loss: 0.0421

 7837/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 410us/step - acc: 0.9852 - loss: 0.0422

 7903/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 413us/step - acc: 0.9852 - loss: 0.0422

 7973/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 416us/step - acc: 0.9852 - loss: 0.0423

 8037/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 419us/step - acc: 0.9852 - loss: 0.0423

 8111/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 421us/step - acc: 0.9852 - loss: 0.0424

 8191/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 423us/step - acc: 0.9851 - loss: 0.0425

 8285/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 424us/step - acc: 0.9851 - loss: 0.0426

 8348/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 427us/step - acc: 0.9851 - loss: 0.0427

 8438/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 428us/step - acc: 0.9851 - loss: 0.0428

 8500/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 431us/step - acc: 0.9850 - loss: 0.0428

 8575/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 434us/step - acc: 0.9850 - loss: 0.0429

 8674/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 434us/step - acc: 0.9850 - loss: 0.0430

 8754/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 436us/step - acc: 0.9850 - loss: 0.0431

 8824/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 438us/step - acc: 0.9849 - loss: 0.0431

 8874/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 443us/step - acc: 0.9849 - loss: 0.0432

 8876/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 450us/step - acc: 0.9849 - loss: 0.0432

 8878/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 456us/step - acc: 0.9849 - loss: 0.0432

 8912/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 459us/step - acc: 0.9849 - loss: 0.0432

 8953/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 463us/step - acc: 0.9849 - loss: 0.0433

 9007/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 466us/step - acc: 0.9849 - loss: 0.0433

 9076/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 468us/step - acc: 0.9849 - loss: 0.0434

 9163/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 469us/step - acc: 0.9848 - loss: 0.0435

 9243/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 470us/step - acc: 0.9848 - loss: 0.0435

 9296/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 473us/step - acc: 0.9848 - loss: 0.0436

 9353/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 475us/step - acc: 0.9848 - loss: 0.0436

 9444/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 476us/step - acc: 0.9848 - loss: 0.0437

 9514/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 478us/step - acc: 0.9848 - loss: 0.0438

 9604/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 479us/step - acc: 0.9847 - loss: 0.0438

 9669/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 481us/step - acc: 0.9847 - loss: 0.0439

 9769/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 481us/step - acc: 0.9847 - loss: 0.0440

 9866/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 481us/step - acc: 0.9847 - loss: 0.0441

 9929/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 483us/step - acc: 0.9846 - loss: 0.0441

10027/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 484us/step - acc: 0.9846 - loss: 0.0442

10132/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 483us/step - acc: 0.9846 - loss: 0.0443

10230/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 484us/step - acc: 0.9846 - loss: 0.0444

10327/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 484us/step - acc: 0.9845 - loss: 0.0444

10446/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 483us/step - acc: 0.9845 - loss: 0.0445

10571/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 482us/step - acc: 0.9845 - loss: 0.0446

10693/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 482us/step - acc: 0.9845 - loss: 0.0448

10818/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 481us/step - acc: 0.9844 - loss: 0.0449

10942/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 480us/step - acc: 0.9844 - loss: 0.0450

11054/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 479us/step - acc: 0.9844 - loss: 0.0450

11170/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 479us/step - acc: 0.9844 - loss: 0.0451

11296/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 478us/step - acc: 0.9843 - loss: 0.0452

11413/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 478us/step - acc: 0.9843 - loss: 0.0453

11542/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 477us/step - acc: 0.9843 - loss: 0.0454

11660/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 476us/step - acc: 0.9842 - loss: 0.0455

11780/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 475us/step - acc: 0.9842 - loss: 0.0456

11901/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 475us/step - acc: 0.9842 - loss: 0.0457

12017/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 474us/step - acc: 0.9842 - loss: 0.0458

12141/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 474us/step - acc: 0.9841 - loss: 0.0459

12225/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 475us/step - acc: 0.9841 - loss: 0.0459

12314/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 475us/step - acc: 0.9841 - loss: 0.0460

12423/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 475us/step - acc: 0.9841 - loss: 0.0461

12537/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 475us/step - acc: 0.9841 - loss: 0.0461

12644/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 475us/step - acc: 0.9840 - loss: 0.0462

12744/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 475us/step - acc: 0.9840 - loss: 0.0463

12849/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 475us/step - acc: 0.9840 - loss: 0.0464

12966/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 475us/step - acc: 0.9840 - loss: 0.0464

13093/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 474us/step - acc: 0.9839 - loss: 0.0465

13211/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 473us/step - acc: 0.9839 - loss: 0.0466

13322/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 473us/step - acc: 0.9839 - loss: 0.0467

13440/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 473us/step - acc: 0.9839 - loss: 0.0467

13556/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 472us/step - acc: 0.9838 - loss: 0.0468

13671/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 472us/step - acc: 0.9838 - loss: 0.0469

13791/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 472us/step - acc: 0.9838 - loss: 0.0470

13909/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 471us/step - acc: 0.9838 - loss: 0.0470

13995/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 472us/step - acc: 0.9838 - loss: 0.0471

14052/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 474us/step - acc: 0.9838 - loss: 0.0471

14126/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 475us/step - acc: 0.9837 - loss: 0.0472

14198/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 476us/step - acc: 0.9837 - loss: 0.0472

14262/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 477us/step - acc: 0.9837 - loss: 0.0473

14327/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 479us/step - acc: 0.9837 - loss: 0.0473

14404/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 479us/step - acc: 0.9837 - loss: 0.0473

14481/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 480us/step - acc: 0.9837 - loss: 0.0474

14509/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 483us/step - acc: 0.9837 - loss: 0.0474

14519/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 487us/step - acc: 0.9837 - loss: 0.0474

14573/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 488us/step - acc: 0.9837 - loss: 0.0474

14650/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 489us/step - acc: 0.9837 - loss: 0.0475

14725/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 490us/step - acc: 0.9837 - loss: 0.0475

14807/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 491us/step - acc: 0.9837 - loss: 0.0476

14894/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 491us/step - acc: 0.9836 - loss: 0.0476

14979/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 492us/step - acc: 0.9836 - loss: 0.0477

15076/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 492us/step - acc: 0.9836 - loss: 0.0477

15160/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 493us/step - acc: 0.9836 - loss: 0.0477

15247/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 493us/step - acc: 0.9836 - loss: 0.0478

15314/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 494us/step - acc: 0.9836 - loss: 0.0478

15416/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 494us/step - acc: 0.9836 - loss: 0.0479

15522/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 494us/step - acc: 0.9836 - loss: 0.0479

15609/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 495us/step - acc: 0.9835 - loss: 0.0479

15683/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 495us/step - acc: 0.9835 - loss: 0.0480

15733/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 497us/step - acc: 0.9835 - loss: 0.0480

15838/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 497us/step - acc: 0.9835 - loss: 0.0481

15912/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 498us/step - acc: 0.9835 - loss: 0.0481

15978/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 499us/step - acc: 0.9835 - loss: 0.0481

16063/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 499us/step - acc: 0.9835 - loss: 0.0482

16159/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 500us/step - acc: 0.9835 - loss: 0.0482

16263/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 499us/step - acc: 0.9835 - loss: 0.0483

16373/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 499us/step - acc: 0.9835 - loss: 0.0483

16476/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 499us/step - acc: 0.9834 - loss: 0.0484

16583/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 499us/step - acc: 0.9834 - loss: 0.0484

16674/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 499us/step - acc: 0.9834 - loss: 0.0485

16767/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 499us/step - acc: 0.9834 - loss: 0.0485

16852/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 500us/step - acc: 0.9834 - loss: 0.0485

16894/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 502us/step - acc: 0.9834 - loss: 0.0486

16916/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 504us/step - acc: 0.9834 - loss: 0.0486

16978/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 505us/step - acc: 0.9834 - loss: 0.0486

17069/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 505us/step - acc: 0.9834 - loss: 0.0486

17140/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 506us/step - acc: 0.9834 - loss: 0.0487

17215/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 507us/step - acc: 0.9833 - loss: 0.0487

17269/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 508us/step - acc: 0.9833 - loss: 0.0487

17342/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 509us/step - acc: 0.9833 - loss: 0.0488

17436/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 509us/step - acc: 0.9833 - loss: 0.0488

17497/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 510us/step - acc: 0.9833 - loss: 0.0488

17545/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 512us/step - acc: 0.9833 - loss: 0.0489

17620/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 513us/step - acc: 0.9833 - loss: 0.0489

17722/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 512us/step - acc: 0.9833 - loss: 0.0489

17811/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 513us/step - acc: 0.9833 - loss: 0.0490

17895/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 513us/step - acc: 0.9833 - loss: 0.0490

17987/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 513us/step - acc: 0.9833 - loss: 0.0491

18074/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 514us/step - acc: 0.9832 - loss: 0.0491

18166/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 514us/step - acc: 0.9832 - loss: 0.0491

18266/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 514us/step - acc: 0.9832 - loss: 0.0492

18366/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 514us/step - acc: 0.9832 - loss: 0.0492

18464/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 514us/step - acc: 0.9832 - loss: 0.0493

18575/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 513us/step - acc: 0.9832 - loss: 0.0493

18689/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 513us/step - acc: 0.9832 - loss: 0.0494

18799/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 513us/step - acc: 0.9832 - loss: 0.0494

18915/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 512us/step - acc: 0.9831 - loss: 0.0495

18984/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 513us/step - acc: 0.9831 - loss: 0.0495

19038/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 514us/step - acc: 0.9831 - loss: 0.0495

19079/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 516us/step - acc: 0.9831 - loss: 0.0495

19116/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 517us/step - acc: 0.9831 - loss: 0.0495

19169/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 519us/step - acc: 0.9831 - loss: 0.0496

19238/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 519us/step - acc: 0.9831 - loss: 0.0496

19328/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 519us/step - acc: 0.9831 - loss: 0.0496

19429/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 519us/step - acc: 0.9831 - loss: 0.0497

19539/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 519us/step - acc: 0.9831 - loss: 0.0497

19655/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 518us/step - acc: 0.9831 - loss: 0.0497

19745/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 519us/step - acc: 0.9831 - loss: 0.0498

19848/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 519us/step - acc: 0.9830 - loss: 0.0498

19957/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 518us/step - acc: 0.9830 - loss: 0.0498

20084/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 517us/step - acc: 0.9830 - loss: 0.0499

20206/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 517us/step - acc: 0.9830 - loss: 0.0499

20313/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 517us/step - acc: 0.9830 - loss: 0.0500

20405/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 517us/step - acc: 0.9830 - loss: 0.0500

20507/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 517us/step - acc: 0.9830 - loss: 0.0500

20616/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 516us/step - acc: 0.9830 - loss: 0.0501

20733/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 516us/step - acc: 0.9830 - loss: 0.0501

20853/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 515us/step - acc: 0.9830 - loss: 0.0501

20937/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 516us/step - acc: 0.9830 - loss: 0.0502

21021/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 516us/step - acc: 0.9829 - loss: 0.0502

21133/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 516us/step - acc: 0.9829 - loss: 0.0502

21262/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 515us/step - acc: 0.9829 - loss: 0.0503

21360/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 515us/step - acc: 0.9829 - loss: 0.0503

21462/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 515us/step - acc: 0.9829 - loss: 0.0503

21570/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 515us/step - acc: 0.9829 - loss: 0.0504

21681/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 514us/step - acc: 0.9829 - loss: 0.0504

21794/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 514us/step - acc: 0.9829 - loss: 0.0504

21900/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 514us/step - acc: 0.9829 - loss: 0.0505

22011/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 513us/step - acc: 0.9829 - loss: 0.0505

22110/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 513us/step - acc: 0.9829 - loss: 0.0505

22208/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 513us/step - acc: 0.9829 - loss: 0.0506

22323/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 513us/step - acc: 0.9828 - loss: 0.0506

22416/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 513us/step - acc: 0.9828 - loss: 0.0506

22533/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 513us/step - acc: 0.9828 - loss: 0.0507

22631/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 513us/step - acc: 0.9828 - loss: 0.0507

22744/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 512us/step - acc: 0.9828 - loss: 0.0507

22861/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 512us/step - acc: 0.9828 - loss: 0.0508

22973/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 512us/step - acc: 0.9828 - loss: 0.0508

23087/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 511us/step - acc: 0.9828 - loss: 0.0508

23205/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 511us/step - acc: 0.9828 - loss: 0.0509

23329/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 510us/step - acc: 0.9828 - loss: 0.0509

23448/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 510us/step - acc: 0.9828 - loss: 0.0509

23566/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 509us/step - acc: 0.9827 - loss: 0.0510

23669/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 509us/step - acc: 0.9827 - loss: 0.0510

23790/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 509us/step - acc: 0.9827 - loss: 0.0510

23923/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 508us/step - acc: 0.9827 - loss: 0.0510

24058/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 507us/step - acc: 0.9827 - loss: 0.0511

24195/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 506us/step - acc: 0.9827 - loss: 0.0511

24313/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 506us/step - acc: 0.9827 - loss: 0.0511

24421/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 506us/step - acc: 0.9827 - loss: 0.0512

24527/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 506us/step - acc: 0.9827 - loss: 0.0512

24630/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 506us/step - acc: 0.9827 - loss: 0.0512

24734/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 506us/step - acc: 0.9827 - loss: 0.0512

24837/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 505us/step - acc: 0.9827 - loss: 0.0512

24947/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 505us/step - acc: 0.9827 - loss: 0.0513

25060/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 505us/step - acc: 0.9827 - loss: 0.0513

25159/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 505us/step - acc: 0.9826 - loss: 0.0513

25239/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 505us/step - acc: 0.9826 - loss: 0.0513

25317/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 506us/step - acc: 0.9826 - loss: 0.0514

25396/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 506us/step - acc: 0.9826 - loss: 0.0514

25505/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 506us/step - acc: 0.9826 - loss: 0.0514

25607/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 506us/step - acc: 0.9826 - loss: 0.0514

25703/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 506us/step - acc: 0.9826 - loss: 0.0514

25796/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 506us/step - acc: 0.9826 - loss: 0.0515

25905/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 506us/step - acc: 0.9826 - loss: 0.0515

26008/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 506us/step - acc: 0.9826 - loss: 0.0515

26114/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 506us/step - acc: 0.9826 - loss: 0.0515

26213/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 506us/step - acc: 0.9826 - loss: 0.0516

26311/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 506us/step - acc: 0.9826 - loss: 0.0516

26413/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 506us/step - acc: 0.9826 - loss: 0.0516

26521/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 506us/step - acc: 0.9826 - loss: 0.0516

26624/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 506us/step - acc: 0.9826 - loss: 0.0516

26734/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 505us/step - acc: 0.9826 - loss: 0.0517

26826/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 506us/step - acc: 0.9826 - loss: 0.0517

26902/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 506us/step - acc: 0.9826 - loss: 0.0517

27009/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 506us/step - acc: 0.9825 - loss: 0.0517

27103/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 506us/step - acc: 0.9825 - loss: 0.0518

27188/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 506us/step - acc: 0.9825 - loss: 0.0518

27270/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 507us/step - acc: 0.9825 - loss: 0.0518

27360/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 507us/step - acc: 0.9825 - loss: 0.0518

27459/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 507us/step - acc: 0.9825 - loss: 0.0518

27546/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 507us/step - acc: 0.9825 - loss: 0.0518

27632/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 507us/step - acc: 0.9825 - loss: 0.0519

27713/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 508us/step - acc: 0.9825 - loss: 0.0519

27807/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 508us/step - acc: 0.9825 - loss: 0.0519

27909/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 508us/step - acc: 0.9825 - loss: 0.0519

28007/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 508us/step - acc: 0.9825 - loss: 0.0519

28108/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 508us/step - acc: 0.9825 - loss: 0.0520

28222/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 507us/step - acc: 0.9825 - loss: 0.0520

28339/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 507us/step - acc: 0.9825 - loss: 0.0520

28453/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 507us/step - acc: 0.9825 - loss: 0.0520

28545/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 507us/step - acc: 0.9825 - loss: 0.0521

28640/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 507us/step - acc: 0.9825 - loss: 0.0521

28739/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 507us/step - acc: 0.9825 - loss: 0.0521

28852/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 507us/step - acc: 0.9825 - loss: 0.0521

28963/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 506us/step - acc: 0.9825 - loss: 0.0521

29083/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 506us/step - acc: 0.9824 - loss: 0.0522

29201/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 506us/step - acc: 0.9824 - loss: 0.0522

29297/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 506us/step - acc: 0.9824 - loss: 0.0522

29413/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 506us/step - acc: 0.9824 - loss: 0.0522

29510/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 506us/step - acc: 0.9824 - loss: 0.0522

29605/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 506us/step - acc: 0.9824 - loss: 0.0523

29714/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 505us/step - acc: 0.9824 - loss: 0.0523

29836/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 505us/step - acc: 0.9824 - loss: 0.0523

29947/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 505us/step - acc: 0.9824 - loss: 0.0523

30066/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 505us/step - acc: 0.9824 - loss: 0.0523

30165/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 505us/step - acc: 0.9824 - loss: 0.0523

30284/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 504us/step - acc: 0.9824 - loss: 0.0524

30392/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 504us/step - acc: 0.9824 - loss: 0.0524

30510/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 504us/step - acc: 0.9824 - loss: 0.0524

30622/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 504us/step - acc: 0.9824 - loss: 0.0524

30723/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 504us/step - acc: 0.9824 - loss: 0.0524

30842/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 503us/step - acc: 0.9824 - loss: 0.0524

30941/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 503us/step - acc: 0.9824 - loss: 0.0525

31030/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 503us/step - acc: 0.9824 - loss: 0.0525

31135/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 503us/step - acc: 0.9824 - loss: 0.0525

31251/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 503us/step - acc: 0.9824 - loss: 0.0525

31362/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 503us/step - acc: 0.9824 - loss: 0.0525

31482/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 503us/step - acc: 0.9824 - loss: 0.0525

31591/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 502us/step - acc: 0.9824 - loss: 0.0526

31692/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 502us/step - acc: 0.9824 - loss: 0.0526

31805/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 502us/step - acc: 0.9824 - loss: 0.0526

31917/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 502us/step - acc: 0.9824 - loss: 0.0526

32048/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 502us/step - acc: 0.9824 - loss: 0.0526

32171/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 501us/step - acc: 0.9824 - loss: 0.0526

32291/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 501us/step - acc: 0.9824 - loss: 0.0527

32417/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 501us/step - acc: 0.9824 - loss: 0.0527

32535/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 500us/step - acc: 0.9823 - loss: 0.0527

32662/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 500us/step - acc: 0.9823 - loss: 0.0527

32784/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 499us/step - acc: 0.9823 - loss: 0.0527

32913/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 499us/step - acc: 0.9823 - loss: 0.0528

33042/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 499us/step - acc: 0.9823 - loss: 0.0528

33160/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 498us/step - acc: 0.9823 - loss: 0.0528

33272/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 498us/step - acc: 0.9823 - loss: 0.0528

33386/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 498us/step - acc: 0.9823 - loss: 0.0528

33444/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 499us/step - acc: 0.9823 - loss: 0.0528

33511/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 499us/step - acc: 0.9823 - loss: 0.0529

33596/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 499us/step - acc: 0.9823 - loss: 0.0529

33687/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 500us/step - acc: 0.9823 - loss: 0.0529

33793/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 499us/step - acc: 0.9823 - loss: 0.0529

33903/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 499us/step - acc: 0.9823 - loss: 0.0529

34020/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 499us/step - acc: 0.9823 - loss: 0.0529

34136/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 499us/step - acc: 0.9823 - loss: 0.0530

34234/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 499us/step - acc: 0.9823 - loss: 0.0530

34321/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 499us/step - acc: 0.9823 - loss: 0.0530

34441/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 499us/step - acc: 0.9823 - loss: 0.0530

34562/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 499us/step - acc: 0.9823 - loss: 0.0530

34686/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 498us/step - acc: 0.9823 - loss: 0.0530

34808/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 498us/step - acc: 0.9823 - loss: 0.0530

34932/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 498us/step - acc: 0.9823 - loss: 0.0531

35044/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 497us/step - acc: 0.9823 - loss: 0.0531

35163/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 497us/step - acc: 0.9823 - loss: 0.0531

35262/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 497us/step - acc: 0.9823 - loss: 0.0531

35345/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 497us/step - acc: 0.9823 - loss: 0.0531

35443/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 497us/step - acc: 0.9823 - loss: 0.0531

35540/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 498us/step - acc: 0.9822 - loss: 0.0531

35644/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 498us/step - acc: 0.9822 - loss: 0.0532

35744/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 498us/step - acc: 0.9822 - loss: 0.0532

35858/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 497us/step - acc: 0.9822 - loss: 0.0532

35975/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 497us/step - acc: 0.9822 - loss: 0.0532

36099/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 497us/step - acc: 0.9822 - loss: 0.0532

36221/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 497us/step - acc: 0.9822 - loss: 0.0532

36345/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 496us/step - acc: 0.9822 - loss: 0.0533

36467/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 496us/step - acc: 0.9822 - loss: 0.0533

36579/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 496us/step - acc: 0.9822 - loss: 0.0533

36699/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 496us/step - acc: 0.9822 - loss: 0.0533

36820/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 495us/step - acc: 0.9822 - loss: 0.0533

36941/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 495us/step - acc: 0.9822 - loss: 0.0534

37056/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 495us/step - acc: 0.9822 - loss: 0.0534

37180/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 494us/step - acc: 0.9822 - loss: 0.0534

37305/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 494us/step - acc: 0.9822 - loss: 0.0534

37424/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 494us/step - acc: 0.9822 - loss: 0.0534

37546/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 494us/step - acc: 0.9822 - loss: 0.0535

37674/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 493us/step - acc: 0.9822 - loss: 0.0535

37804/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 493us/step - acc: 0.9822 - loss: 0.0535

37936/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 493us/step - acc: 0.9822 - loss: 0.0535

38061/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 492us/step - acc: 0.9822 - loss: 0.0535

38187/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 492us/step - acc: 0.9822 - loss: 0.0536

38318/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 492us/step - acc: 0.9821 - loss: 0.0536

38454/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 491us/step - acc: 0.9821 - loss: 0.0536

38590/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 491us/step - acc: 0.9821 - loss: 0.0536

38723/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 490us/step - acc: 0.9821 - loss: 0.0536

38861/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 490us/step - acc: 0.9821 - loss: 0.0537

39000/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 489us/step - acc: 0.9821 - loss: 0.0537

39133/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 489us/step - acc: 0.9821 - loss: 0.0537

39270/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 489us/step - acc: 0.9821 - loss: 0.0537

39406/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 488us/step - acc: 0.9821 - loss: 0.0537

39543/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 488us/step - acc: 0.9821 - loss: 0.0538 

39681/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 487us/step - acc: 0.9821 - loss: 0.0538

39817/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 487us/step - acc: 0.9821 - loss: 0.0538

39956/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 487us/step - acc: 0.9821 - loss: 0.0538

40087/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 486us/step - acc: 0.9821 - loss: 0.0538

40218/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 486us/step - acc: 0.9821 - loss: 0.0538

40344/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 486us/step - acc: 0.9821 - loss: 0.0539

40475/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 485us/step - acc: 0.9821 - loss: 0.0539

40608/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 485us/step - acc: 0.9821 - loss: 0.0539

40745/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 484us/step - acc: 0.9821 - loss: 0.0539

40874/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 484us/step - acc: 0.9821 - loss: 0.0539

40991/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 484us/step - acc: 0.9821 - loss: 0.0539

41110/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 484us/step - acc: 0.9821 - loss: 0.0540

41232/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 484us/step - acc: 0.9820 - loss: 0.0540

41368/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 483us/step - acc: 0.9820 - loss: 0.0540

41490/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 483us/step - acc: 0.9820 - loss: 0.0540

41630/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 483us/step - acc: 0.9820 - loss: 0.0540

41770/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 482us/step - acc: 0.9820 - loss: 0.0541

41910/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 482us/step - acc: 0.9820 - loss: 0.0541

42048/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 481us/step - acc: 0.9820 - loss: 0.0541

42186/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 481us/step - acc: 0.9820 - loss: 0.0541

42320/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 481us/step - acc: 0.9820 - loss: 0.0541

42458/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 480us/step - acc: 0.9820 - loss: 0.0541

42595/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 480us/step - acc: 0.9820 - loss: 0.0542

42718/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 480us/step - acc: 0.9820 - loss: 0.0542

42851/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 479us/step - acc: 0.9820 - loss: 0.0542

42986/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 479us/step - acc: 0.9820 - loss: 0.0542

43122/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 479us/step - acc: 0.9820 - loss: 0.0542

43256/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 478us/step - acc: 0.9820 - loss: 0.0542

43394/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 478us/step - acc: 0.9820 - loss: 0.0543

43516/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 478us/step - acc: 0.9820 - loss: 0.0543

43640/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 478us/step - acc: 0.9820 - loss: 0.0543

43776/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 477us/step - acc: 0.9820 - loss: 0.0543

43908/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 477us/step - acc: 0.9820 - loss: 0.0543

44043/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 477us/step - acc: 0.9820 - loss: 0.0543

44176/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 476us/step - acc: 0.9820 - loss: 0.0543

44312/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 476us/step - acc: 0.9820 - loss: 0.0544

44449/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 476us/step - acc: 0.9820 - loss: 0.0544

44584/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 475us/step - acc: 0.9820 - loss: 0.0544

44721/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 475us/step - acc: 0.9820 - loss: 0.0544

44860/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 475us/step - acc: 0.9819 - loss: 0.0544

44996/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 474us/step - acc: 0.9819 - loss: 0.0544

45133/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 474us/step - acc: 0.9819 - loss: 0.0545

45271/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 474us/step - acc: 0.9819 - loss: 0.0545

45411/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 473us/step - acc: 0.9819 - loss: 0.0545

45547/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 473us/step - acc: 0.9819 - loss: 0.0545

45671/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 473us/step - acc: 0.9819 - loss: 0.0545

45801/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 473us/step - acc: 0.9819 - loss: 0.0546

45937/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 472us/step - acc: 0.9819 - loss: 0.0546

46077/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 472us/step - acc: 0.9819 - loss: 0.0546

46208/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 472us/step - acc: 0.9819 - loss: 0.0546

46346/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 471us/step - acc: 0.9819 - loss: 0.0546

46480/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 471us/step - acc: 0.9819 - loss: 0.0546

46616/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 471us/step - acc: 0.9819 - loss: 0.0546

46749/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 471us/step - acc: 0.9819 - loss: 0.0547

46885/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 470us/step - acc: 0.9819 - loss: 0.0547

47014/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 470us/step - acc: 0.9819 - loss: 0.0547

47151/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 470us/step - acc: 0.9819 - loss: 0.0547

47288/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 469us/step - acc: 0.9819 - loss: 0.0547

47427/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 469us/step - acc: 0.9819 - loss: 0.0547

47567/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 469us/step - acc: 0.9819 - loss: 0.0548

47694/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 469us/step - acc: 0.9819 - loss: 0.0548

47827/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 468us/step - acc: 0.9819 - loss: 0.0548

47964/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 468us/step - acc: 0.9819 - loss: 0.0548

48097/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 468us/step - acc: 0.9818 - loss: 0.0548

48234/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 468us/step - acc: 0.9818 - loss: 0.0548

48371/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 467us/step - acc: 0.9818 - loss: 0.0549

48506/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 467us/step - acc: 0.9818 - loss: 0.0549

48641/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 467us/step - acc: 0.9818 - loss: 0.0549

48779/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 466us/step - acc: 0.9818 - loss: 0.0549

48905/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 466us/step - acc: 0.9818 - loss: 0.0549

49043/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 466us/step - acc: 0.9818 - loss: 0.0549

49180/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 466us/step - acc: 0.9818 - loss: 0.0550

49317/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 465us/step - acc: 0.9818 - loss: 0.0550

49454/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 465us/step - acc: 0.9818 - loss: 0.0550

49589/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 465us/step - acc: 0.9818 - loss: 0.0550

49726/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 465us/step - acc: 0.9818 - loss: 0.0550

49858/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 464us/step - acc: 0.9818 - loss: 0.0550

49993/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 464us/step - acc: 0.9818 - loss: 0.0551

50131/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 464us/step - acc: 0.9818 - loss: 0.0551

50261/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 464us/step - acc: 0.9818 - loss: 0.0551

50398/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 463us/step - acc: 0.9818 - loss: 0.0551

50530/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 463us/step - acc: 0.9818 - loss: 0.0551

50667/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 463us/step - acc: 0.9818 - loss: 0.0551

50805/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 463us/step - acc: 0.9818 - loss: 0.0551

50941/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 462us/step - acc: 0.9818 - loss: 0.0552

51079/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 462us/step - acc: 0.9818 - loss: 0.0552

51202/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 462us/step - acc: 0.9818 - loss: 0.0552

51337/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 462us/step - acc: 0.9818 - loss: 0.0552

51473/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 462us/step - acc: 0.9817 - loss: 0.0552

51609/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 461us/step - acc: 0.9817 - loss: 0.0552

51743/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 461us/step - acc: 0.9817 - loss: 0.0553

51875/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 461us/step - acc: 0.9817 - loss: 0.0553

52010/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 461us/step - acc: 0.9817 - loss: 0.0553

52145/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 460us/step - acc: 0.9817 - loss: 0.0553

52275/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 460us/step - acc: 0.9817 - loss: 0.0553

52411/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 460us/step - acc: 0.9817 - loss: 0.0553

52551/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 460us/step - acc: 0.9817 - loss: 0.0554

52689/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 459us/step - acc: 0.9817 - loss: 0.0554

52828/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 459us/step - acc: 0.9817 - loss: 0.0554

52966/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 459us/step - acc: 0.9817 - loss: 0.0554

53105/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 459us/step - acc: 0.9817 - loss: 0.0554

53244/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 458us/step - acc: 0.9817 - loss: 0.0554

53383/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 458us/step - acc: 0.9817 - loss: 0.0554

53522/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 458us/step - acc: 0.9817 - loss: 0.0555

53658/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 458us/step - acc: 0.9817 - loss: 0.0555

53782/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 458us/step - acc: 0.9817 - loss: 0.0555

53900/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 458us/step - acc: 0.9817 - loss: 0.0555

54028/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 457us/step - acc: 0.9817 - loss: 0.0555

54156/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 457us/step - acc: 0.9817 - loss: 0.0555

54285/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 457us/step - acc: 0.9817 - loss: 0.0555

54413/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 457us/step - acc: 0.9817 - loss: 0.0555

54536/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 457us/step - acc: 0.9817 - loss: 0.0556

54664/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 457us/step - acc: 0.9817 - loss: 0.0556

54795/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 456us/step - acc: 0.9817 - loss: 0.0556

54928/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 456us/step - acc: 0.9816 - loss: 0.0556

55065/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 456us/step - acc: 0.9816 - loss: 0.0556

55205/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 456us/step - acc: 0.9816 - loss: 0.0556

55341/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 456us/step - acc: 0.9816 - loss: 0.0556

55474/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 455us/step - acc: 0.9816 - loss: 0.0557

55607/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 455us/step - acc: 0.9816 - loss: 0.0557

55743/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 455us/step - acc: 0.9816 - loss: 0.0557

55869/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 455us/step - acc: 0.9816 - loss: 0.0557

55971/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 455us/step - acc: 0.9816 - loss: 0.0557

56091/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 455us/step - acc: 0.9816 - loss: 0.0557

56222/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 455us/step - acc: 0.9816 - loss: 0.0558

56359/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 454us/step - acc: 0.9816 - loss: 0.0558

56493/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 454us/step - acc: 0.9816 - loss: 0.0558

56612/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 454us/step - acc: 0.9816 - loss: 0.0558

56732/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 454us/step - acc: 0.9816 - loss: 0.0558

56849/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 454us/step - acc: 0.9816 - loss: 0.0558

56966/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 454us/step - acc: 0.9816 - loss: 0.0558

57090/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 454us/step - acc: 0.9816 - loss: 0.0559

57212/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 454us/step - acc: 0.9816 - loss: 0.0559

57336/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 454us/step - acc: 0.9816 - loss: 0.0559

57448/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 454us/step - acc: 0.9816 - loss: 0.0559

57568/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 454us/step - acc: 0.9816 - loss: 0.0559

57693/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 454us/step - acc: 0.9816 - loss: 0.0559

57822/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 453us/step - acc: 0.9816 - loss: 0.0559

57943/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 453us/step - acc: 0.9816 - loss: 0.0560

58076/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 453us/step - acc: 0.9816 - loss: 0.0560

58211/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 453us/step - acc: 0.9815 - loss: 0.0560

58345/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 453us/step - acc: 0.9815 - loss: 0.0560

58483/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 453us/step - acc: 0.9815 - loss: 0.0560

58622/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 452us/step - acc: 0.9815 - loss: 0.0560

58756/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 452us/step - acc: 0.9815 - loss: 0.0561

58894/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 452us/step - acc: 0.9815 - loss: 0.0561

59032/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 452us/step - acc: 0.9815 - loss: 0.0561

59170/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 452us/step - acc: 0.9815 - loss: 0.0561

59298/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 451us/step - acc: 0.9815 - loss: 0.0561

59419/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 451us/step - acc: 0.9815 - loss: 0.0561

59538/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 451us/step - acc: 0.9815 - loss: 0.0561

59655/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 451us/step - acc: 0.9815 - loss: 0.0562

59771/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 451us/step - acc: 0.9815 - loss: 0.0562

59880/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 451us/step - acc: 0.9815 - loss: 0.0562

59907/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 452us/step - acc: 0.9815 - loss: 0.0562

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 517us/step - acc: 0.9815 - loss: 0.0562 - val_acc: 0.9710 - val_loss: 0.1043

Epoch 8/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 11:08 11ms/step - acc: 1.0000 - loss: 0.4715

  132/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 383us/step - acc: 0.9940 - loss: 0.0320 

  267/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 377us/step - acc: 0.9896 - loss: 0.0299

  404/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 373us/step - acc: 0.9890 - loss: 0.0291

  531/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 378us/step - acc: 0.9893 - loss: 0.0281

  663/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 379us/step - acc: 0.9894 - loss: 0.0281

  801/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 376us/step - acc: 0.9892 - loss: 0.0291

  939/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 374us/step - acc: 0.9887 - loss: 0.0306

 1077/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 373us/step - acc: 0.9884 - loss: 0.0317

 1206/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 374us/step - acc: 0.9881 - loss: 0.0325

 1335/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 376us/step - acc: 0.9878 - loss: 0.0334

 1462/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 378us/step - acc: 0.9875 - loss: 0.0344

 1598/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 377us/step - acc: 0.9873 - loss: 0.0352

 1734/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 376us/step - acc: 0.9870 - loss: 0.0360

 1862/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 377us/step - acc: 0.9868 - loss: 0.0368

 2000/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 376us/step - acc: 0.9865 - loss: 0.0376

 2136/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 376us/step - acc: 0.9863 - loss: 0.0383

 2260/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 377us/step - acc: 0.9861 - loss: 0.0389

 2391/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 378us/step - acc: 0.9859 - loss: 0.0394

 2527/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 377us/step - acc: 0.9857 - loss: 0.0398

 2663/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 377us/step - acc: 0.9856 - loss: 0.0401

 2793/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 377us/step - acc: 0.9855 - loss: 0.0403

 2931/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 377us/step - acc: 0.9854 - loss: 0.0406

 3068/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 376us/step - acc: 0.9853 - loss: 0.0409

 3207/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 376us/step - acc: 0.9852 - loss: 0.0412

 3334/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 376us/step - acc: 0.9852 - loss: 0.0414

 3468/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 376us/step - acc: 0.9852 - loss: 0.0417

 3606/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 376us/step - acc: 0.9851 - loss: 0.0419

 3743/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 375us/step - acc: 0.9851 - loss: 0.0422

 3881/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 375us/step - acc: 0.9850 - loss: 0.0424

 4017/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9850 - loss: 0.0426

 4154/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9850 - loss: 0.0428

 4292/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9850 - loss: 0.0429

 4419/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9850 - loss: 0.0430

 4552/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9850 - loss: 0.0431

 4677/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 376us/step - acc: 0.9850 - loss: 0.0432

 4811/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9850 - loss: 0.0434

 4947/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9850 - loss: 0.0435

 5083/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9850 - loss: 0.0436

 5217/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9850 - loss: 0.0437

 5352/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9849 - loss: 0.0439

 5488/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9849 - loss: 0.0441

 5625/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9848 - loss: 0.0443

 5760/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9848 - loss: 0.0445

 5897/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9848 - loss: 0.0448

 6035/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9847 - loss: 0.0450

 6172/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9847 - loss: 0.0452

 6309/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9846 - loss: 0.0454

 6445/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9846 - loss: 0.0455

 6571/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9846 - loss: 0.0457

 6709/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9845 - loss: 0.0459

 6847/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9845 - loss: 0.0460

 6980/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9845 - loss: 0.0462

 7101/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 375us/step - acc: 0.9845 - loss: 0.0463

 7227/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 375us/step - acc: 0.9845 - loss: 0.0464

 7350/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 376us/step - acc: 0.9844 - loss: 0.0465

 7473/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 376us/step - acc: 0.9844 - loss: 0.0466

 7600/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 376us/step - acc: 0.9844 - loss: 0.0468

 7721/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 377us/step - acc: 0.9844 - loss: 0.0469

 7835/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9844 - loss: 0.0470

 7945/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 379us/step - acc: 0.9844 - loss: 0.0471

 8078/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 379us/step - acc: 0.9843 - loss: 0.0472

 8213/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 379us/step - acc: 0.9843 - loss: 0.0474

 8350/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 379us/step - acc: 0.9843 - loss: 0.0475

 8487/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 379us/step - acc: 0.9843 - loss: 0.0476

 8608/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 379us/step - acc: 0.9842 - loss: 0.0477

 8741/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 379us/step - acc: 0.9842 - loss: 0.0478

 8878/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 379us/step - acc: 0.9842 - loss: 0.0479

 9015/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 379us/step - acc: 0.9842 - loss: 0.0480

 9151/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9841 - loss: 0.0482

 9268/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 379us/step - acc: 0.9841 - loss: 0.0482

 9403/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 379us/step - acc: 0.9841 - loss: 0.0483

 9541/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 379us/step - acc: 0.9841 - loss: 0.0484

 9678/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 379us/step - acc: 0.9841 - loss: 0.0485

 9808/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 379us/step - acc: 0.9841 - loss: 0.0486

 9945/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 379us/step - acc: 0.9841 - loss: 0.0487

10076/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 379us/step - acc: 0.9840 - loss: 0.0487

10196/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 379us/step - acc: 0.9840 - loss: 0.0488

10323/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 379us/step - acc: 0.9840 - loss: 0.0488

10446/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 380us/step - acc: 0.9840 - loss: 0.0489

10570/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 380us/step - acc: 0.9840 - loss: 0.0489

10672/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 381us/step - acc: 0.9840 - loss: 0.0490

10782/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 382us/step - acc: 0.9840 - loss: 0.0490

10900/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 382us/step - acc: 0.9840 - loss: 0.0491

11009/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 383us/step - acc: 0.9840 - loss: 0.0491

11132/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 383us/step - acc: 0.9840 - loss: 0.0492

11258/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 383us/step - acc: 0.9840 - loss: 0.0492

11380/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 384us/step - acc: 0.9840 - loss: 0.0492

11495/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 384us/step - acc: 0.9839 - loss: 0.0493

11604/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 385us/step - acc: 0.9839 - loss: 0.0493

11722/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 385us/step - acc: 0.9839 - loss: 0.0494

11841/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 386us/step - acc: 0.9839 - loss: 0.0494

11957/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 386us/step - acc: 0.9839 - loss: 0.0495

12024/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 388us/step - acc: 0.9839 - loss: 0.0495

12132/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 389us/step - acc: 0.9839 - loss: 0.0495

12244/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 389us/step - acc: 0.9839 - loss: 0.0496

12357/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 390us/step - acc: 0.9839 - loss: 0.0496

12474/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 390us/step - acc: 0.9839 - loss: 0.0496

12592/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 391us/step - acc: 0.9839 - loss: 0.0497

12707/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 391us/step - acc: 0.9839 - loss: 0.0497

12811/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 392us/step - acc: 0.9839 - loss: 0.0497

12920/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 392us/step - acc: 0.9839 - loss: 0.0497

13031/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 393us/step - acc: 0.9839 - loss: 0.0498

13143/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 393us/step - acc: 0.9839 - loss: 0.0498

13240/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 394us/step - acc: 0.9839 - loss: 0.0498

13347/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 395us/step - acc: 0.9839 - loss: 0.0499

13448/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 396us/step - acc: 0.9839 - loss: 0.0499

13547/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 397us/step - acc: 0.9839 - loss: 0.0499

13625/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 398us/step - acc: 0.9839 - loss: 0.0499

13681/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 400us/step - acc: 0.9839 - loss: 0.0499

13738/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 402us/step - acc: 0.9839 - loss: 0.0499

13840/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 403us/step - acc: 0.9839 - loss: 0.0500

13937/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 404us/step - acc: 0.9839 - loss: 0.0500

14049/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 404us/step - acc: 0.9839 - loss: 0.0500

14173/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 404us/step - acc: 0.9839 - loss: 0.0500

14296/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 404us/step - acc: 0.9839 - loss: 0.0500

14421/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 404us/step - acc: 0.9839 - loss: 0.0500

14541/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 404us/step - acc: 0.9839 - loss: 0.0501

14660/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 404us/step - acc: 0.9839 - loss: 0.0501

14775/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 404us/step - acc: 0.9839 - loss: 0.0501

14866/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 405us/step - acc: 0.9839 - loss: 0.0501

14954/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 406us/step - acc: 0.9839 - loss: 0.0501

15051/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 407us/step - acc: 0.9839 - loss: 0.0501

15165/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 407us/step - acc: 0.9839 - loss: 0.0501

15272/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 408us/step - acc: 0.9839 - loss: 0.0501

15382/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 408us/step - acc: 0.9839 - loss: 0.0501

15478/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 409us/step - acc: 0.9839 - loss: 0.0501

15576/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 409us/step - acc: 0.9839 - loss: 0.0501

15661/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 410us/step - acc: 0.9839 - loss: 0.0501

15749/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 411us/step - acc: 0.9839 - loss: 0.0502

15857/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 412us/step - acc: 0.9839 - loss: 0.0502

15962/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 412us/step - acc: 0.9839 - loss: 0.0502

16041/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 413us/step - acc: 0.9839 - loss: 0.0502

16152/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 413us/step - acc: 0.9839 - loss: 0.0502

16260/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 414us/step - acc: 0.9839 - loss: 0.0502

16365/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 414us/step - acc: 0.9839 - loss: 0.0502

16489/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 414us/step - acc: 0.9839 - loss: 0.0502

16609/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 414us/step - acc: 0.9839 - loss: 0.0503

16730/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 414us/step - acc: 0.9839 - loss: 0.0503

16853/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 414us/step - acc: 0.9839 - loss: 0.0503

16965/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 414us/step - acc: 0.9839 - loss: 0.0503

17085/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 414us/step - acc: 0.9839 - loss: 0.0503

17209/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 414us/step - acc: 0.9838 - loss: 0.0503

17329/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 414us/step - acc: 0.9838 - loss: 0.0504

17455/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 414us/step - acc: 0.9838 - loss: 0.0504

17568/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 414us/step - acc: 0.9838 - loss: 0.0504

17691/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 414us/step - acc: 0.9838 - loss: 0.0504

17795/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 415us/step - acc: 0.9838 - loss: 0.0504

17842/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 417us/step - acc: 0.9838 - loss: 0.0504

17927/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 417us/step - acc: 0.9838 - loss: 0.0504

17979/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 419us/step - acc: 0.9838 - loss: 0.0504

18014/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 421us/step - acc: 0.9838 - loss: 0.0504

18029/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 424us/step - acc: 0.9838 - loss: 0.0504

18045/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 426us/step - acc: 0.9838 - loss: 0.0504

18057/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 430us/step - acc: 0.9838 - loss: 0.0504

18087/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 432us/step - acc: 0.9838 - loss: 0.0504

18116/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 434us/step - acc: 0.9838 - loss: 0.0505

18245/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 433us/step - acc: 0.9838 - loss: 0.0505

18358/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 433us/step - acc: 0.9838 - loss: 0.0505

18446/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 434us/step - acc: 0.9838 - loss: 0.0505

18549/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 434us/step - acc: 0.9838 - loss: 0.0505

18663/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 434us/step - acc: 0.9838 - loss: 0.0505

18791/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 434us/step - acc: 0.9838 - loss: 0.0505

18908/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 434us/step - acc: 0.9838 - loss: 0.0505

19030/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 434us/step - acc: 0.9838 - loss: 0.0505

19147/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 434us/step - acc: 0.9838 - loss: 0.0506

19229/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 435us/step - acc: 0.9838 - loss: 0.0506

19303/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 436us/step - acc: 0.9838 - loss: 0.0506

19403/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 436us/step - acc: 0.9838 - loss: 0.0506

19523/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 436us/step - acc: 0.9838 - loss: 0.0506

19656/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 435us/step - acc: 0.9838 - loss: 0.0506

19786/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 435us/step - acc: 0.9838 - loss: 0.0506

19912/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 435us/step - acc: 0.9838 - loss: 0.0506

20032/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 435us/step - acc: 0.9838 - loss: 0.0506

20118/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 435us/step - acc: 0.9838 - loss: 0.0507

20239/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 435us/step - acc: 0.9838 - loss: 0.0507

20345/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 436us/step - acc: 0.9838 - loss: 0.0507

20462/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 435us/step - acc: 0.9838 - loss: 0.0507

20578/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 435us/step - acc: 0.9838 - loss: 0.0507

20681/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 436us/step - acc: 0.9838 - loss: 0.0507

20796/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 436us/step - acc: 0.9838 - loss: 0.0507

20921/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 436us/step - acc: 0.9838 - loss: 0.0507

21048/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 435us/step - acc: 0.9838 - loss: 0.0507

21170/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 435us/step - acc: 0.9838 - loss: 0.0508

21292/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 435us/step - acc: 0.9838 - loss: 0.0508

21414/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 435us/step - acc: 0.9838 - loss: 0.0508

21511/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 435us/step - acc: 0.9838 - loss: 0.0508

21575/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 436us/step - acc: 0.9838 - loss: 0.0508

21688/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 436us/step - acc: 0.9838 - loss: 0.0508

21805/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 436us/step - acc: 0.9838 - loss: 0.0508

21927/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 436us/step - acc: 0.9838 - loss: 0.0508

22050/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 436us/step - acc: 0.9838 - loss: 0.0508

22173/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 436us/step - acc: 0.9838 - loss: 0.0508

22299/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 436us/step - acc: 0.9838 - loss: 0.0509

22389/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 436us/step - acc: 0.9838 - loss: 0.0509

22505/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 436us/step - acc: 0.9838 - loss: 0.0509

22621/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 436us/step - acc: 0.9838 - loss: 0.0509

22732/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 436us/step - acc: 0.9838 - loss: 0.0509

22844/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 436us/step - acc: 0.9838 - loss: 0.0509

22952/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 436us/step - acc: 0.9838 - loss: 0.0509

23068/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 436us/step - acc: 0.9838 - loss: 0.0509

23177/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 436us/step - acc: 0.9838 - loss: 0.0509

23267/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 437us/step - acc: 0.9838 - loss: 0.0509

23388/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 437us/step - acc: 0.9838 - loss: 0.0509

23503/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 437us/step - acc: 0.9838 - loss: 0.0509

23625/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 437us/step - acc: 0.9837 - loss: 0.0509

23739/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 437us/step - acc: 0.9837 - loss: 0.0509

23859/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 437us/step - acc: 0.9837 - loss: 0.0509

23979/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 437us/step - acc: 0.9837 - loss: 0.0510

24084/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 437us/step - acc: 0.9837 - loss: 0.0510

24203/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 437us/step - acc: 0.9837 - loss: 0.0510

24324/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 437us/step - acc: 0.9837 - loss: 0.0510

24448/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 436us/step - acc: 0.9837 - loss: 0.0510

24541/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 437us/step - acc: 0.9837 - loss: 0.0510

24606/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 438us/step - acc: 0.9837 - loss: 0.0510

24710/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 438us/step - acc: 0.9837 - loss: 0.0510

24824/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 438us/step - acc: 0.9837 - loss: 0.0510

24928/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 438us/step - acc: 0.9837 - loss: 0.0510

25039/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 438us/step - acc: 0.9837 - loss: 0.0510

25141/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 438us/step - acc: 0.9837 - loss: 0.0510

25253/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 438us/step - acc: 0.9837 - loss: 0.0510

25366/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 438us/step - acc: 0.9837 - loss: 0.0510

25452/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 439us/step - acc: 0.9837 - loss: 0.0510

25535/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 439us/step - acc: 0.9837 - loss: 0.0510

25651/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 439us/step - acc: 0.9837 - loss: 0.0510

25755/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 440us/step - acc: 0.9837 - loss: 0.0510

25862/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 440us/step - acc: 0.9837 - loss: 0.0510

25968/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 440us/step - acc: 0.9837 - loss: 0.0510

26094/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 440us/step - acc: 0.9837 - loss: 0.0510

26199/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 440us/step - acc: 0.9837 - loss: 0.0510

26290/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 440us/step - acc: 0.9837 - loss: 0.0510

26332/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 442us/step - acc: 0.9837 - loss: 0.0510

26408/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 442us/step - acc: 0.9837 - loss: 0.0510

26486/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 443us/step - acc: 0.9837 - loss: 0.0510

26532/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 444us/step - acc: 0.9837 - loss: 0.0510

26603/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 445us/step - acc: 0.9837 - loss: 0.0510

26697/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 445us/step - acc: 0.9837 - loss: 0.0510

26754/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 446us/step - acc: 0.9837 - loss: 0.0510

26859/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 446us/step - acc: 0.9837 - loss: 0.0510

26940/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 447us/step - acc: 0.9837 - loss: 0.0510

27021/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 447us/step - acc: 0.9837 - loss: 0.0510

27128/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 447us/step - acc: 0.9837 - loss: 0.0510

27242/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 447us/step - acc: 0.9837 - loss: 0.0510

27357/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 447us/step - acc: 0.9837 - loss: 0.0510

27458/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 447us/step - acc: 0.9837 - loss: 0.0510

27563/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 447us/step - acc: 0.9837 - loss: 0.0510

27671/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 447us/step - acc: 0.9837 - loss: 0.0510

27755/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 448us/step - acc: 0.9837 - loss: 0.0510

27813/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 449us/step - acc: 0.9837 - loss: 0.0510

27890/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 449us/step - acc: 0.9837 - loss: 0.0510

27990/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 450us/step - acc: 0.9837 - loss: 0.0510

28072/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 450us/step - acc: 0.9837 - loss: 0.0510

28138/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 451us/step - acc: 0.9837 - loss: 0.0510

28189/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 452us/step - acc: 0.9837 - loss: 0.0510

28265/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 452us/step - acc: 0.9837 - loss: 0.0510

28360/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 453us/step - acc: 0.9837 - loss: 0.0511

28470/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 453us/step - acc: 0.9837 - loss: 0.0511

28594/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 452us/step - acc: 0.9837 - loss: 0.0511

28701/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 452us/step - acc: 0.9837 - loss: 0.0511

28809/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 453us/step - acc: 0.9837 - loss: 0.0511

28933/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 452us/step - acc: 0.9837 - loss: 0.0511

29059/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 452us/step - acc: 0.9837 - loss: 0.0511

29172/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 452us/step - acc: 0.9837 - loss: 0.0511

29288/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 452us/step - acc: 0.9837 - loss: 0.0511

29412/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 452us/step - acc: 0.9837 - loss: 0.0511

29484/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 452us/step - acc: 0.9837 - loss: 0.0511

29571/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 453us/step - acc: 0.9837 - loss: 0.0511

29690/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 453us/step - acc: 0.9837 - loss: 0.0511

29791/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 453us/step - acc: 0.9837 - loss: 0.0511

29892/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 453us/step - acc: 0.9837 - loss: 0.0511

30015/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 453us/step - acc: 0.9837 - loss: 0.0511

30139/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 453us/step - acc: 0.9837 - loss: 0.0511

30244/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 453us/step - acc: 0.9837 - loss: 0.0511

30301/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 453us/step - acc: 0.9837 - loss: 0.0511

30329/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 455us/step - acc: 0.9837 - loss: 0.0511

30366/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 456us/step - acc: 0.9837 - loss: 0.0511

30418/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 457us/step - acc: 0.9837 - loss: 0.0511

30478/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 457us/step - acc: 0.9837 - loss: 0.0511

30538/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 458us/step - acc: 0.9837 - loss: 0.0511

30577/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 459us/step - acc: 0.9837 - loss: 0.0511

30631/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 460us/step - acc: 0.9837 - loss: 0.0511

30678/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 461us/step - acc: 0.9837 - loss: 0.0511

30771/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 461us/step - acc: 0.9837 - loss: 0.0511

30883/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 461us/step - acc: 0.9837 - loss: 0.0511

30991/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 461us/step - acc: 0.9837 - loss: 0.0511

31093/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 461us/step - acc: 0.9837 - loss: 0.0511

31168/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 462us/step - acc: 0.9837 - loss: 0.0511

31264/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 462us/step - acc: 0.9837 - loss: 0.0511

31340/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 463us/step - acc: 0.9837 - loss: 0.0511

31425/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 463us/step - acc: 0.9837 - loss: 0.0511

31489/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 464us/step - acc: 0.9837 - loss: 0.0511

31573/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 464us/step - acc: 0.9837 - loss: 0.0511

31629/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 465us/step - acc: 0.9837 - loss: 0.0511

31653/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 466us/step - acc: 0.9837 - loss: 0.0511

31719/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 467us/step - acc: 0.9837 - loss: 0.0511

31796/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 467us/step - acc: 0.9837 - loss: 0.0511

31863/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 468us/step - acc: 0.9837 - loss: 0.0511

31939/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 468us/step - acc: 0.9837 - loss: 0.0511

32015/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 469us/step - acc: 0.9837 - loss: 0.0511

32096/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 469us/step - acc: 0.9837 - loss: 0.0511

32209/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 469us/step - acc: 0.9837 - loss: 0.0511

32322/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 469us/step - acc: 0.9837 - loss: 0.0511

32420/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 469us/step - acc: 0.9837 - loss: 0.0511

32533/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 469us/step - acc: 0.9837 - loss: 0.0511

32639/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 469us/step - acc: 0.9837 - loss: 0.0511

32670/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 470us/step - acc: 0.9837 - loss: 0.0511

32709/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 471us/step - acc: 0.9837 - loss: 0.0511

32740/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 472us/step - acc: 0.9837 - loss: 0.0511

32802/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 473us/step - acc: 0.9837 - loss: 0.0511

32893/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 473us/step - acc: 0.9837 - loss: 0.0511

33001/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 473us/step - acc: 0.9837 - loss: 0.0511

33111/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 473us/step - acc: 0.9837 - loss: 0.0511

33222/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 473us/step - acc: 0.9837 - loss: 0.0511

33316/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 473us/step - acc: 0.9837 - loss: 0.0511

33401/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 474us/step - acc: 0.9837 - loss: 0.0511

33515/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 473us/step - acc: 0.9837 - loss: 0.0511

33597/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 474us/step - acc: 0.9837 - loss: 0.0511

33678/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 474us/step - acc: 0.9837 - loss: 0.0511

33770/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 474us/step - acc: 0.9837 - loss: 0.0511

33886/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 474us/step - acc: 0.9837 - loss: 0.0511

33981/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 474us/step - acc: 0.9837 - loss: 0.0511

34092/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 474us/step - acc: 0.9836 - loss: 0.0511

34219/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 474us/step - acc: 0.9836 - loss: 0.0511

34327/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 474us/step - acc: 0.9836 - loss: 0.0511

34399/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 474us/step - acc: 0.9836 - loss: 0.0511

34493/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 475us/step - acc: 0.9836 - loss: 0.0511

34601/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 475us/step - acc: 0.9836 - loss: 0.0511

34712/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 474us/step - acc: 0.9836 - loss: 0.0511

34844/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 474us/step - acc: 0.9836 - loss: 0.0511

34946/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 474us/step - acc: 0.9836 - loss: 0.0511

35059/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 474us/step - acc: 0.9836 - loss: 0.0511

35168/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 474us/step - acc: 0.9836 - loss: 0.0511

35281/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 474us/step - acc: 0.9836 - loss: 0.0511

35374/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 474us/step - acc: 0.9836 - loss: 0.0511

35456/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 474us/step - acc: 0.9836 - loss: 0.0511

35526/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 475us/step - acc: 0.9836 - loss: 0.0511

35603/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 475us/step - acc: 0.9836 - loss: 0.0511

35720/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 475us/step - acc: 0.9836 - loss: 0.0511

35825/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 475us/step - acc: 0.9836 - loss: 0.0511

35952/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 475us/step - acc: 0.9836 - loss: 0.0511

36071/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 475us/step - acc: 0.9836 - loss: 0.0511

36178/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 475us/step - acc: 0.9836 - loss: 0.0511

36285/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 475us/step - acc: 0.9836 - loss: 0.0511

36371/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 475us/step - acc: 0.9836 - loss: 0.0511

36467/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 475us/step - acc: 0.9836 - loss: 0.0511

36583/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 475us/step - acc: 0.9836 - loss: 0.0511

36695/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 475us/step - acc: 0.9836 - loss: 0.0511

36812/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 475us/step - acc: 0.9836 - loss: 0.0511

36923/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 475us/step - acc: 0.9836 - loss: 0.0511

37008/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 475us/step - acc: 0.9836 - loss: 0.0511

37072/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 475us/step - acc: 0.9836 - loss: 0.0511

37174/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 475us/step - acc: 0.9836 - loss: 0.0511

37281/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 475us/step - acc: 0.9836 - loss: 0.0511

37378/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 476us/step - acc: 0.9836 - loss: 0.0511

37494/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 475us/step - acc: 0.9836 - loss: 0.0511

37614/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 475us/step - acc: 0.9836 - loss: 0.0511

37705/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 475us/step - acc: 0.9836 - loss: 0.0511

37808/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 475us/step - acc: 0.9836 - loss: 0.0511

37905/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 476us/step - acc: 0.9836 - loss: 0.0511

37996/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 476us/step - acc: 0.9836 - loss: 0.0511

38102/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 476us/step - acc: 0.9836 - loss: 0.0511

38215/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 476us/step - acc: 0.9836 - loss: 0.0512

38327/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 476us/step - acc: 0.9836 - loss: 0.0512

38447/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 475us/step - acc: 0.9836 - loss: 0.0512

38566/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 475us/step - acc: 0.9836 - loss: 0.0512

38670/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 475us/step - acc: 0.9836 - loss: 0.0512

38776/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 475us/step - acc: 0.9836 - loss: 0.0512

38875/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 475us/step - acc: 0.9836 - loss: 0.0512

38984/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 475us/step - acc: 0.9836 - loss: 0.0512 

39097/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 475us/step - acc: 0.9836 - loss: 0.0512

39211/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 475us/step - acc: 0.9836 - loss: 0.0512

39313/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 475us/step - acc: 0.9836 - loss: 0.0512

39415/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 475us/step - acc: 0.9836 - loss: 0.0512

39522/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 475us/step - acc: 0.9836 - loss: 0.0512

39623/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 475us/step - acc: 0.9836 - loss: 0.0512

39685/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 476us/step - acc: 0.9836 - loss: 0.0512

39774/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 476us/step - acc: 0.9836 - loss: 0.0512

39887/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 476us/step - acc: 0.9836 - loss: 0.0512

39933/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 477us/step - acc: 0.9836 - loss: 0.0512

40015/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 477us/step - acc: 0.9836 - loss: 0.0512

40112/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 477us/step - acc: 0.9836 - loss: 0.0512

40242/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 477us/step - acc: 0.9836 - loss: 0.0512

40378/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 477us/step - acc: 0.9836 - loss: 0.0512

40490/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 476us/step - acc: 0.9836 - loss: 0.0512

40596/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 476us/step - acc: 0.9836 - loss: 0.0512

40704/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 476us/step - acc: 0.9836 - loss: 0.0512

40816/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 476us/step - acc: 0.9836 - loss: 0.0512

40934/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 476us/step - acc: 0.9836 - loss: 0.0512

41056/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 476us/step - acc: 0.9836 - loss: 0.0512

41178/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 476us/step - acc: 0.9836 - loss: 0.0512

41262/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 476us/step - acc: 0.9836 - loss: 0.0512

41338/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 476us/step - acc: 0.9836 - loss: 0.0512

41422/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 477us/step - acc: 0.9836 - loss: 0.0512

41528/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 477us/step - acc: 0.9836 - loss: 0.0512

41608/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 477us/step - acc: 0.9836 - loss: 0.0512

41693/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 477us/step - acc: 0.9836 - loss: 0.0512

41808/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 477us/step - acc: 0.9836 - loss: 0.0512

41925/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 477us/step - acc: 0.9836 - loss: 0.0512

42008/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 477us/step - acc: 0.9836 - loss: 0.0512

42105/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 477us/step - acc: 0.9836 - loss: 0.0512

42210/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 477us/step - acc: 0.9836 - loss: 0.0512

42325/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 477us/step - acc: 0.9836 - loss: 0.0512

42439/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 477us/step - acc: 0.9836 - loss: 0.0512

42562/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 477us/step - acc: 0.9836 - loss: 0.0513

42669/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 477us/step - acc: 0.9836 - loss: 0.0513

42775/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 477us/step - acc: 0.9836 - loss: 0.0513

42888/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 477us/step - acc: 0.9836 - loss: 0.0513

43005/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 477us/step - acc: 0.9836 - loss: 0.0513

43124/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 476us/step - acc: 0.9836 - loss: 0.0513

43247/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 476us/step - acc: 0.9836 - loss: 0.0513

43376/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 476us/step - acc: 0.9836 - loss: 0.0513

43499/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 476us/step - acc: 0.9836 - loss: 0.0513

43572/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 476us/step - acc: 0.9836 - loss: 0.0513

43689/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 476us/step - acc: 0.9836 - loss: 0.0513

43814/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 476us/step - acc: 0.9836 - loss: 0.0513

43931/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 476us/step - acc: 0.9836 - loss: 0.0513

44030/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 476us/step - acc: 0.9836 - loss: 0.0513

44140/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 476us/step - acc: 0.9836 - loss: 0.0513

44258/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 476us/step - acc: 0.9836 - loss: 0.0513

44377/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 476us/step - acc: 0.9835 - loss: 0.0513

44498/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 475us/step - acc: 0.9835 - loss: 0.0513

44608/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 475us/step - acc: 0.9835 - loss: 0.0513

44733/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 475us/step - acc: 0.9835 - loss: 0.0513

44849/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 475us/step - acc: 0.9835 - loss: 0.0513

44969/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 475us/step - acc: 0.9835 - loss: 0.0513

45092/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 475us/step - acc: 0.9835 - loss: 0.0513

45204/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 475us/step - acc: 0.9835 - loss: 0.0513

45327/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 474us/step - acc: 0.9835 - loss: 0.0513

45423/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 475us/step - acc: 0.9835 - loss: 0.0513

45547/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 474us/step - acc: 0.9835 - loss: 0.0513

45651/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 474us/step - acc: 0.9835 - loss: 0.0513

45759/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 474us/step - acc: 0.9835 - loss: 0.0513

45860/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 474us/step - acc: 0.9835 - loss: 0.0514

45974/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 474us/step - acc: 0.9835 - loss: 0.0514

46091/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 474us/step - acc: 0.9835 - loss: 0.0514

46211/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 474us/step - acc: 0.9835 - loss: 0.0514

46335/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 474us/step - acc: 0.9835 - loss: 0.0514

46442/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 474us/step - acc: 0.9835 - loss: 0.0514

46551/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 474us/step - acc: 0.9835 - loss: 0.0514

46666/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 474us/step - acc: 0.9835 - loss: 0.0514

46786/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 474us/step - acc: 0.9835 - loss: 0.0514

46900/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 474us/step - acc: 0.9835 - loss: 0.0514

47016/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 473us/step - acc: 0.9835 - loss: 0.0514

47132/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 473us/step - acc: 0.9835 - loss: 0.0514

47251/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 473us/step - acc: 0.9835 - loss: 0.0514

47374/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 473us/step - acc: 0.9835 - loss: 0.0514

47498/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 473us/step - acc: 0.9835 - loss: 0.0514

47621/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 473us/step - acc: 0.9835 - loss: 0.0514

47752/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 472us/step - acc: 0.9835 - loss: 0.0515

47877/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 472us/step - acc: 0.9835 - loss: 0.0515

47995/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 472us/step - acc: 0.9835 - loss: 0.0515

48125/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 472us/step - acc: 0.9835 - loss: 0.0515

48215/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 472us/step - acc: 0.9835 - loss: 0.0515

48310/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 472us/step - acc: 0.9835 - loss: 0.0515

48423/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 472us/step - acc: 0.9835 - loss: 0.0515

48548/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 472us/step - acc: 0.9835 - loss: 0.0515

48676/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 472us/step - acc: 0.9835 - loss: 0.0515

48814/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 471us/step - acc: 0.9835 - loss: 0.0515

48955/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 471us/step - acc: 0.9835 - loss: 0.0515

49100/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 471us/step - acc: 0.9835 - loss: 0.0515

49240/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 470us/step - acc: 0.9835 - loss: 0.0516

49383/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 470us/step - acc: 0.9835 - loss: 0.0516

49521/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 470us/step - acc: 0.9835 - loss: 0.0516

49652/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 470us/step - acc: 0.9835 - loss: 0.0516

49778/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 469us/step - acc: 0.9835 - loss: 0.0516

49904/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 469us/step - acc: 0.9835 - loss: 0.0516

50026/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 469us/step - acc: 0.9835 - loss: 0.0516

50156/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 469us/step - acc: 0.9834 - loss: 0.0516

50277/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 469us/step - acc: 0.9834 - loss: 0.0516

50400/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 469us/step - acc: 0.9834 - loss: 0.0516

50527/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 468us/step - acc: 0.9834 - loss: 0.0516

50650/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 468us/step - acc: 0.9834 - loss: 0.0516

50765/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 468us/step - acc: 0.9834 - loss: 0.0517

50859/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 468us/step - acc: 0.9834 - loss: 0.0517

50987/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 468us/step - acc: 0.9834 - loss: 0.0517

51103/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 468us/step - acc: 0.9834 - loss: 0.0517

51217/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 468us/step - acc: 0.9834 - loss: 0.0517

51337/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 468us/step - acc: 0.9834 - loss: 0.0517

51457/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 468us/step - acc: 0.9834 - loss: 0.0517

51584/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 468us/step - acc: 0.9834 - loss: 0.0517

51706/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 467us/step - acc: 0.9834 - loss: 0.0517

51825/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 467us/step - acc: 0.9834 - loss: 0.0517

51947/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 467us/step - acc: 0.9834 - loss: 0.0517

52060/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 467us/step - acc: 0.9834 - loss: 0.0517

52186/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 467us/step - acc: 0.9834 - loss: 0.0517

52310/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 467us/step - acc: 0.9834 - loss: 0.0517

52434/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 467us/step - acc: 0.9834 - loss: 0.0518

52547/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 467us/step - acc: 0.9834 - loss: 0.0518

52648/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 467us/step - acc: 0.9834 - loss: 0.0518

52772/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 467us/step - acc: 0.9834 - loss: 0.0518

52893/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9834 - loss: 0.0518

53023/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9834 - loss: 0.0518

53075/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 467us/step - acc: 0.9834 - loss: 0.0518

53162/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 467us/step - acc: 0.9834 - loss: 0.0518

53267/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 467us/step - acc: 0.9834 - loss: 0.0518

53370/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 467us/step - acc: 0.9834 - loss: 0.0518

53489/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 467us/step - acc: 0.9834 - loss: 0.0518

53607/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 467us/step - acc: 0.9834 - loss: 0.0518

53733/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 467us/step - acc: 0.9834 - loss: 0.0518

53853/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 466us/step - acc: 0.9834 - loss: 0.0519

53980/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 466us/step - acc: 0.9834 - loss: 0.0519

54105/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 466us/step - acc: 0.9834 - loss: 0.0519

54222/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 466us/step - acc: 0.9833 - loss: 0.0519

54341/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 466us/step - acc: 0.9833 - loss: 0.0519

54464/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 466us/step - acc: 0.9833 - loss: 0.0519

54588/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 466us/step - acc: 0.9833 - loss: 0.0519

54711/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 466us/step - acc: 0.9833 - loss: 0.0519

54830/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 466us/step - acc: 0.9833 - loss: 0.0519

54930/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 466us/step - acc: 0.9833 - loss: 0.0519

55049/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 465us/step - acc: 0.9833 - loss: 0.0519

55164/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 465us/step - acc: 0.9833 - loss: 0.0519

55264/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 466us/step - acc: 0.9833 - loss: 0.0520

55306/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 466us/step - acc: 0.9833 - loss: 0.0520

55366/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 467us/step - acc: 0.9833 - loss: 0.0520

55425/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 467us/step - acc: 0.9833 - loss: 0.0520

55499/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 467us/step - acc: 0.9833 - loss: 0.0520

55600/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 467us/step - acc: 0.9833 - loss: 0.0520

55680/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 467us/step - acc: 0.9833 - loss: 0.0520

55765/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 468us/step - acc: 0.9833 - loss: 0.0520

55850/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 468us/step - acc: 0.9833 - loss: 0.0520

55963/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 468us/step - acc: 0.9833 - loss: 0.0520

56073/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 468us/step - acc: 0.9833 - loss: 0.0520

56194/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 468us/step - acc: 0.9833 - loss: 0.0520

56283/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 468us/step - acc: 0.9833 - loss: 0.0520

56392/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 468us/step - acc: 0.9833 - loss: 0.0520

56506/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 468us/step - acc: 0.9833 - loss: 0.0521

56626/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 468us/step - acc: 0.9833 - loss: 0.0521

56741/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 468us/step - acc: 0.9833 - loss: 0.0521

56849/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 468us/step - acc: 0.9833 - loss: 0.0521

56966/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 468us/step - acc: 0.9833 - loss: 0.0521

57085/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 467us/step - acc: 0.9833 - loss: 0.0521

57203/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 467us/step - acc: 0.9833 - loss: 0.0521

57319/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 467us/step - acc: 0.9833 - loss: 0.0521

57429/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 467us/step - acc: 0.9833 - loss: 0.0521

57525/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 467us/step - acc: 0.9833 - loss: 0.0521

57629/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 467us/step - acc: 0.9833 - loss: 0.0521

57734/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 467us/step - acc: 0.9832 - loss: 0.0522

57798/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 468us/step - acc: 0.9832 - loss: 0.0522

57873/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0522

57968/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0522

58076/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0522

58188/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0522

58298/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0522

58389/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0522

58507/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0522

58597/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0522

58697/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0522

58803/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0522

58921/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0523

59041/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0523

59156/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0523

59264/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0523

59370/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0523

59480/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0523

59590/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0523

59689/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0523

59803/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0523

59910/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 468us/step - acc: 0.9832 - loss: 0.0523

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 532us/step - acc: 0.9832 - loss: 0.0523 - val_acc: 0.9682 - val_loss: 0.1117

Epoch 9/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 18:21 18ms/step - acc: 1.0000 - loss: 0.0011

  128/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 394us/step - acc: 0.9972 - loss: 0.0303 

  265/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 380us/step - acc: 0.9935 - loss: 0.0339

  401/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 377us/step - acc: 0.9911 - loss: 0.0414

  535/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 376us/step - acc: 0.9903 - loss: 0.0435

  670/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 376us/step - acc: 0.9898 - loss: 0.0435

  797/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 379us/step - acc: 0.9894 - loss: 0.0436

  930/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 379us/step - acc: 0.9892 - loss: 0.0432

 1069/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 376us/step - acc: 0.9890 - loss: 0.0427

 1206/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 375us/step - acc: 0.9887 - loss: 0.0426

 1343/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 375us/step - acc: 0.9882 - loss: 0.0428

 1481/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 374us/step - acc: 0.9878 - loss: 0.0432

 1620/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 373us/step - acc: 0.9875 - loss: 0.0436

 1757/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 372us/step - acc: 0.9872 - loss: 0.0438

 1894/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 372us/step - acc: 0.9870 - loss: 0.0439

 2019/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 373us/step - acc: 0.9869 - loss: 0.0441

 2151/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 374us/step - acc: 0.9866 - loss: 0.0445

 2286/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 374us/step - acc: 0.9864 - loss: 0.0449

 2409/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 375us/step - acc: 0.9862 - loss: 0.0452

 2544/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 375us/step - acc: 0.9861 - loss: 0.0454

 2686/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 374us/step - acc: 0.9860 - loss: 0.0456

 2816/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 375us/step - acc: 0.9858 - loss: 0.0458

 2950/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 375us/step - acc: 0.9857 - loss: 0.0460

 3077/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 376us/step - acc: 0.9855 - loss: 0.0461

 3208/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 376us/step - acc: 0.9854 - loss: 0.0462

 3334/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 377us/step - acc: 0.9853 - loss: 0.0463

 3462/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 377us/step - acc: 0.9852 - loss: 0.0464

 3592/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 378us/step - acc: 0.9850 - loss: 0.0465

 3720/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 378us/step - acc: 0.9849 - loss: 0.0467

 3850/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 378us/step - acc: 0.9847 - loss: 0.0468

 3985/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 378us/step - acc: 0.9846 - loss: 0.0470

 4117/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 378us/step - acc: 0.9845 - loss: 0.0471

 4261/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 377us/step - acc: 0.9844 - loss: 0.0472

 4400/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 377us/step - acc: 0.9842 - loss: 0.0474

 4537/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 377us/step - acc: 0.9841 - loss: 0.0475

 4668/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 377us/step - acc: 0.9840 - loss: 0.0476

 4801/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 377us/step - acc: 0.9839 - loss: 0.0477

 4936/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 377us/step - acc: 0.9839 - loss: 0.0478

 5070/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 377us/step - acc: 0.9838 - loss: 0.0479

 5202/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 377us/step - acc: 0.9837 - loss: 0.0480

 5326/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 377us/step - acc: 0.9836 - loss: 0.0480

 5458/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 377us/step - acc: 0.9836 - loss: 0.0481

 5600/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 377us/step - acc: 0.9835 - loss: 0.0481

 5738/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 376us/step - acc: 0.9835 - loss: 0.0482

 5878/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 376us/step - acc: 0.9834 - loss: 0.0483

 6018/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 376us/step - acc: 0.9834 - loss: 0.0483

 6161/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9833 - loss: 0.0484

 6291/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9833 - loss: 0.0485

 6410/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 376us/step - acc: 0.9832 - loss: 0.0485

 6528/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 377us/step - acc: 0.9832 - loss: 0.0486

 6669/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 377us/step - acc: 0.9832 - loss: 0.0486

 6804/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 376us/step - acc: 0.9831 - loss: 0.0487

 6940/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 376us/step - acc: 0.9831 - loss: 0.0487

 7075/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 376us/step - acc: 0.9831 - loss: 0.0488

 7209/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 376us/step - acc: 0.9831 - loss: 0.0488

 7348/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 376us/step - acc: 0.9830 - loss: 0.0489

 7479/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 376us/step - acc: 0.9830 - loss: 0.0489

 7617/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 376us/step - acc: 0.9830 - loss: 0.0489

 7758/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 375us/step - acc: 0.9830 - loss: 0.0490

 7891/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 375us/step - acc: 0.9830 - loss: 0.0490

 8026/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 375us/step - acc: 0.9829 - loss: 0.0490

 8151/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 376us/step - acc: 0.9829 - loss: 0.0490

 8281/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 376us/step - acc: 0.9829 - loss: 0.0490

 8411/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 376us/step - acc: 0.9829 - loss: 0.0491

 8546/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 376us/step - acc: 0.9829 - loss: 0.0491

 8683/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 376us/step - acc: 0.9829 - loss: 0.0491

 8820/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 376us/step - acc: 0.9829 - loss: 0.0491

 8959/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 375us/step - acc: 0.9828 - loss: 0.0491

 9094/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 375us/step - acc: 0.9828 - loss: 0.0491

 9230/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 375us/step - acc: 0.9828 - loss: 0.0491

 9367/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 375us/step - acc: 0.9828 - loss: 0.0491

 9503/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 375us/step - acc: 0.9828 - loss: 0.0491

 9641/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 375us/step - acc: 0.9828 - loss: 0.0491

 9779/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 375us/step - acc: 0.9828 - loss: 0.0492

 9913/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 375us/step - acc: 0.9828 - loss: 0.0492

10040/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 375us/step - acc: 0.9828 - loss: 0.0492

10143/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 376us/step - acc: 0.9828 - loss: 0.0492

10250/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9828 - loss: 0.0492

10376/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9828 - loss: 0.0492

10503/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 378us/step - acc: 0.9828 - loss: 0.0492

10616/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 378us/step - acc: 0.9828 - loss: 0.0492

10729/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 379us/step - acc: 0.9828 - loss: 0.0492

10850/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 379us/step - acc: 0.9828 - loss: 0.0492

10976/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 380us/step - acc: 0.9828 - loss: 0.0492

11102/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 380us/step - acc: 0.9828 - loss: 0.0492

11216/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 381us/step - acc: 0.9828 - loss: 0.0491

11340/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 381us/step - acc: 0.9828 - loss: 0.0491

11458/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 381us/step - acc: 0.9828 - loss: 0.0491

11579/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 382us/step - acc: 0.9828 - loss: 0.0491

11669/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 383us/step - acc: 0.9828 - loss: 0.0491

11791/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 383us/step - acc: 0.9828 - loss: 0.0491

11898/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 384us/step - acc: 0.9828 - loss: 0.0491

12012/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 385us/step - acc: 0.9828 - loss: 0.0491

12138/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 385us/step - acc: 0.9828 - loss: 0.0491

12264/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 385us/step - acc: 0.9828 - loss: 0.0491

12393/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 385us/step - acc: 0.9828 - loss: 0.0491

12521/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 385us/step - acc: 0.9828 - loss: 0.0491

12650/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 385us/step - acc: 0.9828 - loss: 0.0491

12776/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 385us/step - acc: 0.9829 - loss: 0.0491

12898/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 385us/step - acc: 0.9829 - loss: 0.0490

13019/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 386us/step - acc: 0.9829 - loss: 0.0490

13146/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 386us/step - acc: 0.9829 - loss: 0.0490

13273/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 386us/step - acc: 0.9829 - loss: 0.0490

13397/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 386us/step - acc: 0.9829 - loss: 0.0490

13524/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 386us/step - acc: 0.9829 - loss: 0.0490

13653/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 386us/step - acc: 0.9829 - loss: 0.0489

13787/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 386us/step - acc: 0.9829 - loss: 0.0489

13915/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 386us/step - acc: 0.9829 - loss: 0.0489

14050/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 386us/step - acc: 0.9829 - loss: 0.0489

14186/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 386us/step - acc: 0.9829 - loss: 0.0489

14323/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 386us/step - acc: 0.9829 - loss: 0.0489

14452/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 386us/step - acc: 0.9829 - loss: 0.0490

14585/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 386us/step - acc: 0.9829 - loss: 0.0490

14716/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 385us/step - acc: 0.9830 - loss: 0.0490

14850/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 385us/step - acc: 0.9830 - loss: 0.0490

14976/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 385us/step - acc: 0.9830 - loss: 0.0490

15100/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 386us/step - acc: 0.9830 - loss: 0.0490

15237/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 385us/step - acc: 0.9830 - loss: 0.0490

15370/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 385us/step - acc: 0.9830 - loss: 0.0490

15504/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 385us/step - acc: 0.9830 - loss: 0.0490

15638/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 385us/step - acc: 0.9830 - loss: 0.0490

15768/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 385us/step - acc: 0.9830 - loss: 0.0490

15904/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 385us/step - acc: 0.9830 - loss: 0.0490

16031/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 385us/step - acc: 0.9830 - loss: 0.0490

16152/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 385us/step - acc: 0.9830 - loss: 0.0490

16274/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 386us/step - acc: 0.9830 - loss: 0.0490

16392/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 386us/step - acc: 0.9830 - loss: 0.0490

16522/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 386us/step - acc: 0.9830 - loss: 0.0490

16660/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 386us/step - acc: 0.9830 - loss: 0.0491

16792/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 386us/step - acc: 0.9830 - loss: 0.0491

16928/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 386us/step - acc: 0.9830 - loss: 0.0491

17062/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 385us/step - acc: 0.9830 - loss: 0.0491

17209/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 385us/step - acc: 0.9830 - loss: 0.0491

17345/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 385us/step - acc: 0.9830 - loss: 0.0492

17483/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 385us/step - acc: 0.9830 - loss: 0.0492

17620/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 385us/step - acc: 0.9830 - loss: 0.0492

17749/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 385us/step - acc: 0.9830 - loss: 0.0492

17873/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 385us/step - acc: 0.9830 - loss: 0.0492

17998/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 385us/step - acc: 0.9830 - loss: 0.0493

18134/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 385us/step - acc: 0.9830 - loss: 0.0493

18270/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 385us/step - acc: 0.9830 - loss: 0.0493

18397/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 385us/step - acc: 0.9830 - loss: 0.0493

18532/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 385us/step - acc: 0.9830 - loss: 0.0494

18667/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 385us/step - acc: 0.9830 - loss: 0.0494

18801/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 385us/step - acc: 0.9830 - loss: 0.0494

18940/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 384us/step - acc: 0.9830 - loss: 0.0494

19070/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 384us/step - acc: 0.9830 - loss: 0.0495

19207/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 384us/step - acc: 0.9830 - loss: 0.0495

19344/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 384us/step - acc: 0.9830 - loss: 0.0495

19481/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 384us/step - acc: 0.9830 - loss: 0.0495

19618/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 384us/step - acc: 0.9830 - loss: 0.0496

19750/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 384us/step - acc: 0.9830 - loss: 0.0496

19883/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 384us/step - acc: 0.9830 - loss: 0.0496

20018/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 384us/step - acc: 0.9830 - loss: 0.0496

20152/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 384us/step - acc: 0.9830 - loss: 0.0497

20287/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 384us/step - acc: 0.9830 - loss: 0.0497

20418/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 384us/step - acc: 0.9830 - loss: 0.0497

20555/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 383us/step - acc: 0.9830 - loss: 0.0497

20692/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 383us/step - acc: 0.9830 - loss: 0.0498

20831/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 383us/step - acc: 0.9829 - loss: 0.0498

20965/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 383us/step - acc: 0.9829 - loss: 0.0498

21098/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 383us/step - acc: 0.9829 - loss: 0.0498

21234/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 383us/step - acc: 0.9829 - loss: 0.0498

21368/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 383us/step - acc: 0.9829 - loss: 0.0499

21502/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 383us/step - acc: 0.9829 - loss: 0.0499

21638/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 383us/step - acc: 0.9829 - loss: 0.0499

21773/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 383us/step - acc: 0.9829 - loss: 0.0499

21909/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 383us/step - acc: 0.9829 - loss: 0.0500

22047/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 383us/step - acc: 0.9829 - loss: 0.0500

22181/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 382us/step - acc: 0.9829 - loss: 0.0500

22317/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 382us/step - acc: 0.9829 - loss: 0.0500

22455/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 382us/step - acc: 0.9829 - loss: 0.0501

22591/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 382us/step - acc: 0.9829 - loss: 0.0501

22729/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 382us/step - acc: 0.9829 - loss: 0.0501

22867/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 382us/step - acc: 0.9829 - loss: 0.0501

23002/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 382us/step - acc: 0.9829 - loss: 0.0502

23137/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 382us/step - acc: 0.9829 - loss: 0.0502

23274/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 382us/step - acc: 0.9829 - loss: 0.0502

23411/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 382us/step - acc: 0.9829 - loss: 0.0502

23545/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 382us/step - acc: 0.9829 - loss: 0.0503

23668/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 382us/step - acc: 0.9828 - loss: 0.0503

23799/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 382us/step - acc: 0.9828 - loss: 0.0503

23935/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 382us/step - acc: 0.9828 - loss: 0.0503

24067/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 382us/step - acc: 0.9828 - loss: 0.0503

24195/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 382us/step - acc: 0.9828 - loss: 0.0504

24322/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 382us/step - acc: 0.9828 - loss: 0.0504

24445/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 382us/step - acc: 0.9828 - loss: 0.0504

24573/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 382us/step - acc: 0.9828 - loss: 0.0504

24697/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 382us/step - acc: 0.9828 - loss: 0.0504

24816/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 382us/step - acc: 0.9828 - loss: 0.0505

24920/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 383us/step - acc: 0.9828 - loss: 0.0505

25040/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 383us/step - acc: 0.9828 - loss: 0.0505

25161/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 383us/step - acc: 0.9828 - loss: 0.0505

25281/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 383us/step - acc: 0.9828 - loss: 0.0505

25403/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 383us/step - acc: 0.9828 - loss: 0.0506

25528/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 383us/step - acc: 0.9828 - loss: 0.0506

25653/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 384us/step - acc: 0.9828 - loss: 0.0506

25771/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 384us/step - acc: 0.9828 - loss: 0.0506

25894/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 384us/step - acc: 0.9828 - loss: 0.0506

26019/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 384us/step - acc: 0.9828 - loss: 0.0506

26142/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 384us/step - acc: 0.9828 - loss: 0.0507

26260/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 384us/step - acc: 0.9828 - loss: 0.0507

26387/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 384us/step - acc: 0.9828 - loss: 0.0507

26512/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 384us/step - acc: 0.9828 - loss: 0.0507

26629/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 385us/step - acc: 0.9828 - loss: 0.0507

26759/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 385us/step - acc: 0.9828 - loss: 0.0507

26881/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 385us/step - acc: 0.9828 - loss: 0.0507

27003/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 385us/step - acc: 0.9828 - loss: 0.0508

27117/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 385us/step - acc: 0.9828 - loss: 0.0508

27227/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 385us/step - acc: 0.9828 - loss: 0.0508

27341/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 386us/step - acc: 0.9828 - loss: 0.0508

27459/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 386us/step - acc: 0.9828 - loss: 0.0508

27575/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 386us/step - acc: 0.9828 - loss: 0.0508

27692/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 386us/step - acc: 0.9828 - loss: 0.0508

27810/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 386us/step - acc: 0.9828 - loss: 0.0508

27935/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 386us/step - acc: 0.9828 - loss: 0.0508

28052/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 387us/step - acc: 0.9828 - loss: 0.0509

28162/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 387us/step - acc: 0.9828 - loss: 0.0509

28266/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 387us/step - acc: 0.9828 - loss: 0.0509

28380/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 387us/step - acc: 0.9827 - loss: 0.0509

28503/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 387us/step - acc: 0.9827 - loss: 0.0509

28631/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 387us/step - acc: 0.9827 - loss: 0.0509

28751/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 388us/step - acc: 0.9827 - loss: 0.0509

28875/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 388us/step - acc: 0.9827 - loss: 0.0509

28995/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 388us/step - acc: 0.9827 - loss: 0.0509

29109/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 388us/step - acc: 0.9827 - loss: 0.0510

29225/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 388us/step - acc: 0.9827 - loss: 0.0510

29333/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 388us/step - acc: 0.9827 - loss: 0.0510

29448/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 389us/step - acc: 0.9827 - loss: 0.0510

29556/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 389us/step - acc: 0.9827 - loss: 0.0510

29643/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 389us/step - acc: 0.9827 - loss: 0.0510

29721/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9827 - loss: 0.0510

29828/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9827 - loss: 0.0510

29943/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 391us/step - acc: 0.9827 - loss: 0.0510

30059/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 391us/step - acc: 0.9827 - loss: 0.0510

30157/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 391us/step - acc: 0.9827 - loss: 0.0510

30241/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 392us/step - acc: 0.9827 - loss: 0.0510

30324/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 392us/step - acc: 0.9827 - loss: 0.0510

30409/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 393us/step - acc: 0.9827 - loss: 0.0510

30519/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 393us/step - acc: 0.9827 - loss: 0.0510

30624/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 394us/step - acc: 0.9827 - loss: 0.0510

30741/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 394us/step - acc: 0.9827 - loss: 0.0511

30851/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 394us/step - acc: 0.9827 - loss: 0.0511

30953/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 394us/step - acc: 0.9827 - loss: 0.0511

31075/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 394us/step - acc: 0.9827 - loss: 0.0511

31189/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 394us/step - acc: 0.9827 - loss: 0.0511

31295/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 395us/step - acc: 0.9827 - loss: 0.0511

31410/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 395us/step - acc: 0.9827 - loss: 0.0511

31521/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 395us/step - acc: 0.9827 - loss: 0.0511

31625/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 395us/step - acc: 0.9827 - loss: 0.0511

31740/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 396us/step - acc: 0.9827 - loss: 0.0511

31869/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 396us/step - acc: 0.9827 - loss: 0.0511

31984/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 396us/step - acc: 0.9827 - loss: 0.0511

32101/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 396us/step - acc: 0.9827 - loss: 0.0511

32217/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 396us/step - acc: 0.9827 - loss: 0.0511

32326/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 396us/step - acc: 0.9827 - loss: 0.0511

32437/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 396us/step - acc: 0.9827 - loss: 0.0511

32555/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 396us/step - acc: 0.9827 - loss: 0.0511

32663/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 397us/step - acc: 0.9827 - loss: 0.0511

32774/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 397us/step - acc: 0.9827 - loss: 0.0512

32882/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 397us/step - acc: 0.9827 - loss: 0.0512

33006/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 397us/step - acc: 0.9827 - loss: 0.0512

33119/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 397us/step - acc: 0.9827 - loss: 0.0512

33206/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 398us/step - acc: 0.9827 - loss: 0.0512

33289/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 398us/step - acc: 0.9827 - loss: 0.0512

33399/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 398us/step - acc: 0.9827 - loss: 0.0512

33520/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 399us/step - acc: 0.9827 - loss: 0.0512

33640/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 399us/step - acc: 0.9827 - loss: 0.0512

33750/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 399us/step - acc: 0.9827 - loss: 0.0512

33843/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 399us/step - acc: 0.9827 - loss: 0.0512

33923/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 400us/step - acc: 0.9827 - loss: 0.0512

34024/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 400us/step - acc: 0.9827 - loss: 0.0512

34116/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 400us/step - acc: 0.9827 - loss: 0.0512

34233/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 400us/step - acc: 0.9827 - loss: 0.0512

34351/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 401us/step - acc: 0.9827 - loss: 0.0512

34461/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 401us/step - acc: 0.9827 - loss: 0.0512

34577/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 401us/step - acc: 0.9827 - loss: 0.0512

34691/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 401us/step - acc: 0.9827 - loss: 0.0512

34809/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 401us/step - acc: 0.9827 - loss: 0.0512

34935/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 401us/step - acc: 0.9827 - loss: 0.0512

35049/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 401us/step - acc: 0.9827 - loss: 0.0512

35172/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 401us/step - acc: 0.9827 - loss: 0.0512 

35298/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 401us/step - acc: 0.9827 - loss: 0.0513

35416/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 401us/step - acc: 0.9827 - loss: 0.0513

35501/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 402us/step - acc: 0.9827 - loss: 0.0513

35601/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 402us/step - acc: 0.9827 - loss: 0.0513

35706/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 402us/step - acc: 0.9827 - loss: 0.0513

35815/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 402us/step - acc: 0.9827 - loss: 0.0513

35917/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 403us/step - acc: 0.9827 - loss: 0.0513

36039/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 403us/step - acc: 0.9827 - loss: 0.0513

36168/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 403us/step - acc: 0.9827 - loss: 0.0513

36287/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 403us/step - acc: 0.9827 - loss: 0.0513

36406/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 403us/step - acc: 0.9827 - loss: 0.0513

36526/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 403us/step - acc: 0.9827 - loss: 0.0513

36649/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 403us/step - acc: 0.9827 - loss: 0.0513

36760/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 403us/step - acc: 0.9827 - loss: 0.0513

36880/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 403us/step - acc: 0.9827 - loss: 0.0513

36999/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 403us/step - acc: 0.9827 - loss: 0.0513

37121/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 403us/step - acc: 0.9827 - loss: 0.0513

37240/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 403us/step - acc: 0.9827 - loss: 0.0513

37358/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 403us/step - acc: 0.9827 - loss: 0.0513

37484/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 403us/step - acc: 0.9827 - loss: 0.0513

37606/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 403us/step - acc: 0.9827 - loss: 0.0513

37730/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 403us/step - acc: 0.9827 - loss: 0.0514

37842/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 403us/step - acc: 0.9827 - loss: 0.0514

37976/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 403us/step - acc: 0.9827 - loss: 0.0514

38113/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 403us/step - acc: 0.9827 - loss: 0.0514

38241/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 403us/step - acc: 0.9827 - loss: 0.0514

38352/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 403us/step - acc: 0.9827 - loss: 0.0514

38471/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 403us/step - acc: 0.9827 - loss: 0.0514

38588/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 403us/step - acc: 0.9827 - loss: 0.0514

38713/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 403us/step - acc: 0.9827 - loss: 0.0514

38836/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 403us/step - acc: 0.9827 - loss: 0.0514

38962/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 403us/step - acc: 0.9827 - loss: 0.0514

39083/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 403us/step - acc: 0.9827 - loss: 0.0514

39204/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 403us/step - acc: 0.9827 - loss: 0.0514

39321/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 404us/step - acc: 0.9827 - loss: 0.0514

39448/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 404us/step - acc: 0.9827 - loss: 0.0514

39569/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 404us/step - acc: 0.9827 - loss: 0.0514

39689/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 404us/step - acc: 0.9827 - loss: 0.0515

39808/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 404us/step - acc: 0.9827 - loss: 0.0515

39935/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 404us/step - acc: 0.9827 - loss: 0.0515

40066/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 404us/step - acc: 0.9827 - loss: 0.0515

40189/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 404us/step - acc: 0.9827 - loss: 0.0515

40303/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 404us/step - acc: 0.9827 - loss: 0.0515

40433/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 404us/step - acc: 0.9827 - loss: 0.0515

40552/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 404us/step - acc: 0.9827 - loss: 0.0515

40649/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 404us/step - acc: 0.9826 - loss: 0.0515

40754/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 404us/step - acc: 0.9826 - loss: 0.0515

40863/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 404us/step - acc: 0.9826 - loss: 0.0515

40975/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 404us/step - acc: 0.9826 - loss: 0.0515

41095/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 404us/step - acc: 0.9826 - loss: 0.0515

41213/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.9826 - loss: 0.0515

41330/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.9826 - loss: 0.0515

41443/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.9826 - loss: 0.0515

41555/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.9826 - loss: 0.0515

41653/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.9826 - loss: 0.0515

41769/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.9826 - loss: 0.0515

41888/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.9826 - loss: 0.0515

42005/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.9826 - loss: 0.0516

42121/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.9826 - loss: 0.0516

42243/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.9826 - loss: 0.0516

42358/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 405us/step - acc: 0.9826 - loss: 0.0516

42475/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 406us/step - acc: 0.9826 - loss: 0.0516

42580/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 406us/step - acc: 0.9826 - loss: 0.0516

42648/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 406us/step - acc: 0.9826 - loss: 0.0516

42759/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 406us/step - acc: 0.9826 - loss: 0.0516

42842/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 407us/step - acc: 0.9826 - loss: 0.0516

42911/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 407us/step - acc: 0.9826 - loss: 0.0516

42983/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 408us/step - acc: 0.9826 - loss: 0.0516

43032/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 408us/step - acc: 0.9826 - loss: 0.0516

43135/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 409us/step - acc: 0.9826 - loss: 0.0516

43241/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 409us/step - acc: 0.9826 - loss: 0.0516

43344/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 409us/step - acc: 0.9826 - loss: 0.0516

43446/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 409us/step - acc: 0.9826 - loss: 0.0516

43546/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 409us/step - acc: 0.9826 - loss: 0.0516

43642/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 410us/step - acc: 0.9826 - loss: 0.0516

43743/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 410us/step - acc: 0.9826 - loss: 0.0516

43858/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 410us/step - acc: 0.9826 - loss: 0.0517

43971/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 410us/step - acc: 0.9826 - loss: 0.0517

44066/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 410us/step - acc: 0.9826 - loss: 0.0517

44185/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 410us/step - acc: 0.9826 - loss: 0.0517

44300/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 410us/step - acc: 0.9826 - loss: 0.0517

44416/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 411us/step - acc: 0.9826 - loss: 0.0517

44527/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 411us/step - acc: 0.9826 - loss: 0.0517

44618/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 411us/step - acc: 0.9826 - loss: 0.0517

44726/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 411us/step - acc: 0.9826 - loss: 0.0517

44842/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 411us/step - acc: 0.9826 - loss: 0.0517

44956/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 411us/step - acc: 0.9826 - loss: 0.0517

45067/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 411us/step - acc: 0.9826 - loss: 0.0517

45168/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 411us/step - acc: 0.9826 - loss: 0.0517

45277/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 412us/step - acc: 0.9826 - loss: 0.0517

45386/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 412us/step - acc: 0.9826 - loss: 0.0518

45494/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 412us/step - acc: 0.9826 - loss: 0.0518

45612/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 412us/step - acc: 0.9826 - loss: 0.0518

45726/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 412us/step - acc: 0.9826 - loss: 0.0518

45824/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 412us/step - acc: 0.9826 - loss: 0.0518

45926/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 412us/step - acc: 0.9826 - loss: 0.0518

46037/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 412us/step - acc: 0.9826 - loss: 0.0518

46142/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 413us/step - acc: 0.9826 - loss: 0.0518

46242/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 413us/step - acc: 0.9826 - loss: 0.0518

46359/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 413us/step - acc: 0.9826 - loss: 0.0518

46473/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 413us/step - acc: 0.9825 - loss: 0.0518

46584/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 413us/step - acc: 0.9825 - loss: 0.0518

46691/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 413us/step - acc: 0.9825 - loss: 0.0518

46805/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 413us/step - acc: 0.9825 - loss: 0.0518

46893/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 413us/step - acc: 0.9825 - loss: 0.0518

46999/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 414us/step - acc: 0.9825 - loss: 0.0519

47110/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 414us/step - acc: 0.9825 - loss: 0.0519

47231/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 414us/step - acc: 0.9825 - loss: 0.0519

47342/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 414us/step - acc: 0.9825 - loss: 0.0519

47436/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 414us/step - acc: 0.9825 - loss: 0.0519

47552/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 414us/step - acc: 0.9825 - loss: 0.0519

47669/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 414us/step - acc: 0.9825 - loss: 0.0519

47777/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 414us/step - acc: 0.9825 - loss: 0.0519

47887/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 414us/step - acc: 0.9825 - loss: 0.0519

48010/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 414us/step - acc: 0.9825 - loss: 0.0519

48130/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 414us/step - acc: 0.9825 - loss: 0.0519

48226/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9825 - loss: 0.0519

48345/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9825 - loss: 0.0519

48445/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9825 - loss: 0.0519

48554/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9825 - loss: 0.0519

48675/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9825 - loss: 0.0519

48799/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9825 - loss: 0.0519

48919/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9825 - loss: 0.0520

49043/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9825 - loss: 0.0520

49164/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9825 - loss: 0.0520

49278/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9825 - loss: 0.0520

49400/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9825 - loss: 0.0520

49526/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9825 - loss: 0.0520

49652/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9825 - loss: 0.0520

49774/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9825 - loss: 0.0520

49894/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9825 - loss: 0.0520

50017/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9825 - loss: 0.0520

50126/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9825 - loss: 0.0520

50242/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9825 - loss: 0.0520

50360/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9825 - loss: 0.0520

50482/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9825 - loss: 0.0520

50582/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9825 - loss: 0.0520

50693/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9825 - loss: 0.0520

50816/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9825 - loss: 0.0520

50933/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9825 - loss: 0.0521

51049/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9825 - loss: 0.0521

51171/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9825 - loss: 0.0521

51305/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9825 - loss: 0.0521

51440/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9825 - loss: 0.0521

51575/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9825 - loss: 0.0521

51711/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9825 - loss: 0.0521

51848/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9825 - loss: 0.0521

51973/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9825 - loss: 0.0521

52112/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 414us/step - acc: 0.9825 - loss: 0.0521

52252/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 414us/step - acc: 0.9824 - loss: 0.0521

52374/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 414us/step - acc: 0.9824 - loss: 0.0521

52506/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 414us/step - acc: 0.9824 - loss: 0.0521

52637/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 414us/step - acc: 0.9824 - loss: 0.0521

52772/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 414us/step - acc: 0.9824 - loss: 0.0522

52909/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 414us/step - acc: 0.9824 - loss: 0.0522

53048/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 414us/step - acc: 0.9824 - loss: 0.0522

53182/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 414us/step - acc: 0.9824 - loss: 0.0522

53311/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 414us/step - acc: 0.9824 - loss: 0.0522

53448/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 413us/step - acc: 0.9824 - loss: 0.0522

53588/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 413us/step - acc: 0.9824 - loss: 0.0522

53730/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 413us/step - acc: 0.9824 - loss: 0.0522

53874/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 413us/step - acc: 0.9824 - loss: 0.0522

54010/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 413us/step - acc: 0.9824 - loss: 0.0522

54149/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 413us/step - acc: 0.9824 - loss: 0.0522

54287/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 413us/step - acc: 0.9824 - loss: 0.0522

54426/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 412us/step - acc: 0.9824 - loss: 0.0522

54561/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 412us/step - acc: 0.9824 - loss: 0.0523

54698/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 412us/step - acc: 0.9824 - loss: 0.0523

54822/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 412us/step - acc: 0.9824 - loss: 0.0523

54950/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 412us/step - acc: 0.9824 - loss: 0.0523

55094/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 412us/step - acc: 0.9824 - loss: 0.0523

55217/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 412us/step - acc: 0.9824 - loss: 0.0523

55359/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 412us/step - acc: 0.9824 - loss: 0.0523

55484/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 412us/step - acc: 0.9824 - loss: 0.0523

55617/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 412us/step - acc: 0.9824 - loss: 0.0523

55745/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 412us/step - acc: 0.9824 - loss: 0.0523

55888/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 412us/step - acc: 0.9824 - loss: 0.0523

56017/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 412us/step - acc: 0.9824 - loss: 0.0523

56153/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 411us/step - acc: 0.9824 - loss: 0.0523

56285/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 411us/step - acc: 0.9824 - loss: 0.0523

56409/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 411us/step - acc: 0.9824 - loss: 0.0523

56542/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 411us/step - acc: 0.9824 - loss: 0.0524

56678/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 411us/step - acc: 0.9824 - loss: 0.0524

56809/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 411us/step - acc: 0.9824 - loss: 0.0524

56933/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 411us/step - acc: 0.9824 - loss: 0.0524

57069/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 411us/step - acc: 0.9824 - loss: 0.0524

57207/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 411us/step - acc: 0.9824 - loss: 0.0524

57343/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 411us/step - acc: 0.9824 - loss: 0.0524

57481/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 411us/step - acc: 0.9824 - loss: 0.0524

57616/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 411us/step - acc: 0.9824 - loss: 0.0524

57754/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 410us/step - acc: 0.9824 - loss: 0.0524

57890/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 410us/step - acc: 0.9824 - loss: 0.0524

58025/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 410us/step - acc: 0.9824 - loss: 0.0524

58161/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 410us/step - acc: 0.9824 - loss: 0.0524

58299/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 410us/step - acc: 0.9824 - loss: 0.0524

58435/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 410us/step - acc: 0.9824 - loss: 0.0524

58547/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 410us/step - acc: 0.9824 - loss: 0.0524

58644/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 410us/step - acc: 0.9824 - loss: 0.0525

58712/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 411us/step - acc: 0.9824 - loss: 0.0525

58789/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 411us/step - acc: 0.9824 - loss: 0.0525

58909/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 411us/step - acc: 0.9824 - loss: 0.0525

59027/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 411us/step - acc: 0.9824 - loss: 0.0525

59161/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 411us/step - acc: 0.9824 - loss: 0.0525

59297/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 411us/step - acc: 0.9824 - loss: 0.0525

59433/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 411us/step - acc: 0.9823 - loss: 0.0525

59568/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 411us/step - acc: 0.9823 - loss: 0.0525

59705/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 410us/step - acc: 0.9823 - loss: 0.0525

59841/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 410us/step - acc: 0.9823 - loss: 0.0525

59975/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 410us/step - acc: 0.9823 - loss: 0.0525

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 470us/step - acc: 0.9823 - loss: 0.0525 - val_acc: 0.9714 - val_loss: 0.1028

Epoch 10/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 9:20 9ms/step - acc: 1.0000 - loss: 1.7881e-06

  135/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 373us/step - acc: 0.9830 - loss: 0.0461   

  272/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 369us/step - acc: 0.9849 - loss: 0.0435

  411/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 366us/step - acc: 0.9845 - loss: 0.0452

  547/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 367us/step - acc: 0.9847 - loss: 0.0489

  681/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 369us/step - acc: 0.9847 - loss: 0.0513

  812/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 371us/step - acc: 0.9846 - loss: 0.0528

  947/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 371us/step - acc: 0.9847 - loss: 0.0534

 1085/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 370us/step - acc: 0.9847 - loss: 0.0538

 1221/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 370us/step - acc: 0.9846 - loss: 0.0539

 1360/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 369us/step - acc: 0.9846 - loss: 0.0539

 1495/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 369us/step - acc: 0.9845 - loss: 0.0539

 1628/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 370us/step - acc: 0.9845 - loss: 0.0537

 1753/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 372us/step - acc: 0.9845 - loss: 0.0534

 1890/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 372us/step - acc: 0.9845 - loss: 0.0531

 2028/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 371us/step - acc: 0.9846 - loss: 0.0526

 2163/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 371us/step - acc: 0.9847 - loss: 0.0522

 2296/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 372us/step - acc: 0.9848 - loss: 0.0518

 2427/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 372us/step - acc: 0.9848 - loss: 0.0515

 2562/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 372us/step - acc: 0.9849 - loss: 0.0511

 2698/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 372us/step - acc: 0.9849 - loss: 0.0507

 2834/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 372us/step - acc: 0.9850 - loss: 0.0505

 2967/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 372us/step - acc: 0.9850 - loss: 0.0504

 3089/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 374us/step - acc: 0.9850 - loss: 0.0504

 3217/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 374us/step - acc: 0.9850 - loss: 0.0503

 3352/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 374us/step - acc: 0.9850 - loss: 0.0503

 3488/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 374us/step - acc: 0.9849 - loss: 0.0502

 3621/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 374us/step - acc: 0.9849 - loss: 0.0500

 3758/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 374us/step - acc: 0.9849 - loss: 0.0499

 3894/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 374us/step - acc: 0.9849 - loss: 0.0498

 4030/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 373us/step - acc: 0.9849 - loss: 0.0497

 4167/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 373us/step - acc: 0.9849 - loss: 0.0496

 4302/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 373us/step - acc: 0.9849 - loss: 0.0496

 4441/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 373us/step - acc: 0.9848 - loss: 0.0496

 4578/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 373us/step - acc: 0.9848 - loss: 0.0497

 4714/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9848 - loss: 0.0497

 4850/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9847 - loss: 0.0497

 4985/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9847 - loss: 0.0498

 5123/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9847 - loss: 0.0498

 5258/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9846 - loss: 0.0498

 5391/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9846 - loss: 0.0499

 5527/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9846 - loss: 0.0500

 5664/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9845 - loss: 0.0501

 5802/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9845 - loss: 0.0501

 5939/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9845 - loss: 0.0501

 6079/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 371us/step - acc: 0.9845 - loss: 0.0502

 6212/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 371us/step - acc: 0.9845 - loss: 0.0502

 6332/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 372us/step - acc: 0.9844 - loss: 0.0502

 6464/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 372us/step - acc: 0.9844 - loss: 0.0502

 6601/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 372us/step - acc: 0.9844 - loss: 0.0502

 6738/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 372us/step - acc: 0.9844 - loss: 0.0502

 6875/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 372us/step - acc: 0.9844 - loss: 0.0502

 7011/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 372us/step - acc: 0.9844 - loss: 0.0502

 7151/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 372us/step - acc: 0.9844 - loss: 0.0501

 7287/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 372us/step - acc: 0.9844 - loss: 0.0501

 7423/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 372us/step - acc: 0.9844 - loss: 0.0501

 7560/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 372us/step - acc: 0.9844 - loss: 0.0501

 7683/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 372us/step - acc: 0.9844 - loss: 0.0500

 7814/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 372us/step - acc: 0.9844 - loss: 0.0500

 7949/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 372us/step - acc: 0.9843 - loss: 0.0500

 8078/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 373us/step - acc: 0.9843 - loss: 0.0499

 8200/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 373us/step - acc: 0.9843 - loss: 0.0499

 8323/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9843 - loss: 0.0499

 8454/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9843 - loss: 0.0498

 8579/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9843 - loss: 0.0498

 8709/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9843 - loss: 0.0498

 8845/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9843 - loss: 0.0498

 8981/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9843 - loss: 0.0497

 9112/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9843 - loss: 0.0497

 9246/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 374us/step - acc: 0.9843 - loss: 0.0497

 9376/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 374us/step - acc: 0.9843 - loss: 0.0497

 9510/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 374us/step - acc: 0.9842 - loss: 0.0497

 9638/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 375us/step - acc: 0.9842 - loss: 0.0497

 9764/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 375us/step - acc: 0.9842 - loss: 0.0496

 9884/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 376us/step - acc: 0.9842 - loss: 0.0496

10002/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 376us/step - acc: 0.9842 - loss: 0.0496

10119/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9842 - loss: 0.0496

10245/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9842 - loss: 0.0496

10379/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9842 - loss: 0.0496

10506/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9842 - loss: 0.0495

10640/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9842 - loss: 0.0495

10773/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9842 - loss: 0.0495

10907/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9842 - loss: 0.0495

11043/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9842 - loss: 0.0495

11180/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9842 - loss: 0.0494

11319/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9842 - loss: 0.0494

11453/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9841 - loss: 0.0494

11577/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9841 - loss: 0.0494

11705/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9841 - loss: 0.0494

11840/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9841 - loss: 0.0494

11971/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9841 - loss: 0.0494

12104/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9841 - loss: 0.0494

12238/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 377us/step - acc: 0.9841 - loss: 0.0494

12372/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9841 - loss: 0.0494

12504/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9841 - loss: 0.0494

12641/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9841 - loss: 0.0494

12777/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9841 - loss: 0.0494

12910/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9841 - loss: 0.0494

13047/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9841 - loss: 0.0494

13181/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9841 - loss: 0.0494

13314/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9841 - loss: 0.0494

13447/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9841 - loss: 0.0494

13580/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9841 - loss: 0.0494

13713/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9841 - loss: 0.0493

13851/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9841 - loss: 0.0493

13988/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9841 - loss: 0.0493

14122/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 376us/step - acc: 0.9841 - loss: 0.0493

14255/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9841 - loss: 0.0493

14389/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 376us/step - acc: 0.9841 - loss: 0.0493

14526/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 376us/step - acc: 0.9841 - loss: 0.0493

14664/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 376us/step - acc: 0.9841 - loss: 0.0493

14799/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 376us/step - acc: 0.9841 - loss: 0.0494

14937/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9841 - loss: 0.0494

15078/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9841 - loss: 0.0494

15213/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9841 - loss: 0.0494

15350/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9841 - loss: 0.0494

15485/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9841 - loss: 0.0493

15618/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9841 - loss: 0.0493

15747/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9841 - loss: 0.0493

15882/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9841 - loss: 0.0493

16014/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9841 - loss: 0.0493

16140/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9841 - loss: 0.0493

16271/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9841 - loss: 0.0493

16408/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9841 - loss: 0.0493

16545/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9841 - loss: 0.0493

16684/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9841 - loss: 0.0493

16819/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9841 - loss: 0.0493

16949/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9841 - loss: 0.0493

17078/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9841 - loss: 0.0493

17205/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9841 - loss: 0.0493

17340/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9841 - loss: 0.0492

17474/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9841 - loss: 0.0492

17611/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9841 - loss: 0.0492

17749/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9841 - loss: 0.0492

17887/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9841 - loss: 0.0492

18026/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9841 - loss: 0.0492

18167/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9841 - loss: 0.0492

18304/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 375us/step - acc: 0.9842 - loss: 0.0492

18439/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 375us/step - acc: 0.9842 - loss: 0.0492

18565/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9842 - loss: 0.0491

18677/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9842 - loss: 0.0491

18801/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9842 - loss: 0.0491

18921/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 377us/step - acc: 0.9842 - loss: 0.0491

19050/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 377us/step - acc: 0.9842 - loss: 0.0491

19174/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 377us/step - acc: 0.9842 - loss: 0.0491

19301/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 377us/step - acc: 0.9842 - loss: 0.0491

19434/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 377us/step - acc: 0.9842 - loss: 0.0491

19553/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 377us/step - acc: 0.9842 - loss: 0.0490

19679/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 377us/step - acc: 0.9842 - loss: 0.0490

19806/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 377us/step - acc: 0.9842 - loss: 0.0490

19931/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 378us/step - acc: 0.9842 - loss: 0.0490

20052/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 378us/step - acc: 0.9842 - loss: 0.0490

20155/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 378us/step - acc: 0.9842 - loss: 0.0490

20252/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 379us/step - acc: 0.9842 - loss: 0.0490

20332/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 380us/step - acc: 0.9842 - loss: 0.0490

20392/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 381us/step - acc: 0.9842 - loss: 0.0490

20495/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 382us/step - acc: 0.9842 - loss: 0.0489

20581/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 383us/step - acc: 0.9842 - loss: 0.0489

20676/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 383us/step - acc: 0.9842 - loss: 0.0489

20771/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 384us/step - acc: 0.9842 - loss: 0.0489

20873/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 385us/step - acc: 0.9842 - loss: 0.0489

20990/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 385us/step - acc: 0.9842 - loss: 0.0489

21102/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 385us/step - acc: 0.9842 - loss: 0.0489

21208/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 386us/step - acc: 0.9842 - loss: 0.0489

21320/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 386us/step - acc: 0.9842 - loss: 0.0489

21431/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 386us/step - acc: 0.9842 - loss: 0.0489

21546/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 387us/step - acc: 0.9842 - loss: 0.0489

21663/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 387us/step - acc: 0.9842 - loss: 0.0488

21779/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 387us/step - acc: 0.9842 - loss: 0.0488

21904/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 387us/step - acc: 0.9842 - loss: 0.0488

22021/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 387us/step - acc: 0.9842 - loss: 0.0488

22144/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 387us/step - acc: 0.9842 - loss: 0.0488

22257/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 388us/step - acc: 0.9843 - loss: 0.0488

22376/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 388us/step - acc: 0.9843 - loss: 0.0488

22467/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 389us/step - acc: 0.9843 - loss: 0.0488

22564/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 389us/step - acc: 0.9843 - loss: 0.0487

22670/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 390us/step - acc: 0.9843 - loss: 0.0487

22784/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 390us/step - acc: 0.9843 - loss: 0.0487

22896/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 390us/step - acc: 0.9843 - loss: 0.0487

23003/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 390us/step - acc: 0.9843 - loss: 0.0487

23120/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 391us/step - acc: 0.9843 - loss: 0.0487

23217/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 391us/step - acc: 0.9843 - loss: 0.0487

23323/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 392us/step - acc: 0.9843 - loss: 0.0487

23406/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 392us/step - acc: 0.9843 - loss: 0.0486

23509/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 393us/step - acc: 0.9843 - loss: 0.0486

23601/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 393us/step - acc: 0.9843 - loss: 0.0486

23713/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 394us/step - acc: 0.9843 - loss: 0.0486

23800/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 394us/step - acc: 0.9843 - loss: 0.0486

23921/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 394us/step - acc: 0.9843 - loss: 0.0486

24042/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 395us/step - acc: 0.9843 - loss: 0.0486

24168/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 395us/step - acc: 0.9843 - loss: 0.0485

24280/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 395us/step - acc: 0.9843 - loss: 0.0485

24359/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 396us/step - acc: 0.9843 - loss: 0.0485

24465/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 396us/step - acc: 0.9843 - loss: 0.0485

24564/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 396us/step - acc: 0.9843 - loss: 0.0485

24676/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 397us/step - acc: 0.9843 - loss: 0.0485

24789/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 397us/step - acc: 0.9843 - loss: 0.0485

24909/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 397us/step - acc: 0.9843 - loss: 0.0485

24996/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 398us/step - acc: 0.9843 - loss: 0.0485

25045/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 399us/step - acc: 0.9843 - loss: 0.0485

25046/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 401us/step - acc: 0.9843 - loss: 0.0485

25146/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 401us/step - acc: 0.9843 - loss: 0.0484

25256/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 402us/step - acc: 0.9843 - loss: 0.0484

25371/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 402us/step - acc: 0.9843 - loss: 0.0484

25489/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 402us/step - acc: 0.9843 - loss: 0.0484

25597/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 402us/step - acc: 0.9843 - loss: 0.0484

25710/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 402us/step - acc: 0.9843 - loss: 0.0484

25827/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 402us/step - acc: 0.9843 - loss: 0.0484

25943/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 403us/step - acc: 0.9843 - loss: 0.0484

26052/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 403us/step - acc: 0.9843 - loss: 0.0483

26158/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 403us/step - acc: 0.9843 - loss: 0.0483

26231/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 404us/step - acc: 0.9843 - loss: 0.0483

26291/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 405us/step - acc: 0.9843 - loss: 0.0483

26332/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 406us/step - acc: 0.9843 - loss: 0.0483

26355/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 408us/step - acc: 0.9843 - loss: 0.0483

26404/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 409us/step - acc: 0.9843 - loss: 0.0483

26453/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 410us/step - acc: 0.9843 - loss: 0.0483

26528/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 411us/step - acc: 0.9843 - loss: 0.0483

26613/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 411us/step - acc: 0.9843 - loss: 0.0483

26711/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 412us/step - acc: 0.9844 - loss: 0.0483

26815/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 412us/step - acc: 0.9844 - loss: 0.0483

26934/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 412us/step - acc: 0.9844 - loss: 0.0483

27058/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 412us/step - acc: 0.9844 - loss: 0.0483

27139/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 413us/step - acc: 0.9844 - loss: 0.0483

27236/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 413us/step - acc: 0.9844 - loss: 0.0483

27343/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 413us/step - acc: 0.9844 - loss: 0.0483

27445/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 414us/step - acc: 0.9844 - loss: 0.0482

27542/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 414us/step - acc: 0.9844 - loss: 0.0482

27650/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 414us/step - acc: 0.9844 - loss: 0.0482

27769/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 414us/step - acc: 0.9844 - loss: 0.0482

27879/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 414us/step - acc: 0.9844 - loss: 0.0482

27982/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 415us/step - acc: 0.9844 - loss: 0.0482

28100/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 415us/step - acc: 0.9844 - loss: 0.0482

28220/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 415us/step - acc: 0.9844 - loss: 0.0482

28337/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 415us/step - acc: 0.9844 - loss: 0.0482

28458/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 415us/step - acc: 0.9844 - loss: 0.0482

28552/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 415us/step - acc: 0.9844 - loss: 0.0482

28613/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 416us/step - acc: 0.9844 - loss: 0.0482

28662/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 417us/step - acc: 0.9844 - loss: 0.0482

28739/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 418us/step - acc: 0.9844 - loss: 0.0482

28832/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 418us/step - acc: 0.9844 - loss: 0.0481

28943/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 418us/step - acc: 0.9844 - loss: 0.0481

29057/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 418us/step - acc: 0.9844 - loss: 0.0481

29123/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 419us/step - acc: 0.9844 - loss: 0.0481

29188/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 420us/step - acc: 0.9844 - loss: 0.0481

29253/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 421us/step - acc: 0.9844 - loss: 0.0481

29337/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 421us/step - acc: 0.9844 - loss: 0.0481

29439/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 421us/step - acc: 0.9844 - loss: 0.0481

29534/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9844 - loss: 0.0481

29635/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9844 - loss: 0.0481

29733/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9844 - loss: 0.0481

29831/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 423us/step - acc: 0.9844 - loss: 0.0481

29939/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 423us/step - acc: 0.9844 - loss: 0.0481

30050/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 423us/step - acc: 0.9844 - loss: 0.0481

30155/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 423us/step - acc: 0.9844 - loss: 0.0481

30258/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 423us/step - acc: 0.9844 - loss: 0.0481

30319/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 424us/step - acc: 0.9844 - loss: 0.0480

30364/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 425us/step - acc: 0.9844 - loss: 0.0480

30416/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 426us/step - acc: 0.9844 - loss: 0.0480

30480/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 427us/step - acc: 0.9844 - loss: 0.0480

30575/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 427us/step - acc: 0.9844 - loss: 0.0480

30674/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 427us/step - acc: 0.9844 - loss: 0.0480

30779/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 428us/step - acc: 0.9844 - loss: 0.0480

30863/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 428us/step - acc: 0.9844 - loss: 0.0480

30922/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 429us/step - acc: 0.9844 - loss: 0.0480

30993/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 430us/step - acc: 0.9844 - loss: 0.0480

31076/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 430us/step - acc: 0.9844 - loss: 0.0480

31158/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 431us/step - acc: 0.9844 - loss: 0.0480

31236/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 431us/step - acc: 0.9844 - loss: 0.0480

31316/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 432us/step - acc: 0.9844 - loss: 0.0480

31409/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 432us/step - acc: 0.9844 - loss: 0.0480

31463/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 433us/step - acc: 0.9844 - loss: 0.0480

31494/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 435us/step - acc: 0.9844 - loss: 0.0480

31504/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 436us/step - acc: 0.9844 - loss: 0.0480

31559/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 437us/step - acc: 0.9844 - loss: 0.0480

31620/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 438us/step - acc: 0.9844 - loss: 0.0480

31664/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 439us/step - acc: 0.9844 - loss: 0.0480

31734/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 439us/step - acc: 0.9844 - loss: 0.0480

31781/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 440us/step - acc: 0.9844 - loss: 0.0480

31835/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 441us/step - acc: 0.9844 - loss: 0.0480

31898/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 442us/step - acc: 0.9844 - loss: 0.0479

31955/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 443us/step - acc: 0.9844 - loss: 0.0479

32019/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 443us/step - acc: 0.9844 - loss: 0.0479

32054/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 444us/step - acc: 0.9844 - loss: 0.0479

32099/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 445us/step - acc: 0.9844 - loss: 0.0479

32153/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 446us/step - acc: 0.9844 - loss: 0.0479

32206/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 447us/step - acc: 0.9844 - loss: 0.0479

32275/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 448us/step - acc: 0.9844 - loss: 0.0479

32338/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 448us/step - acc: 0.9844 - loss: 0.0479

32423/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 449us/step - acc: 0.9844 - loss: 0.0479

32507/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 449us/step - acc: 0.9844 - loss: 0.0479

32594/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 449us/step - acc: 0.9844 - loss: 0.0479

32689/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 450us/step - acc: 0.9844 - loss: 0.0479

32792/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 450us/step - acc: 0.9844 - loss: 0.0479

32888/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 450us/step - acc: 0.9844 - loss: 0.0479

32979/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 450us/step - acc: 0.9844 - loss: 0.0479

33060/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 451us/step - acc: 0.9844 - loss: 0.0479

33149/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 451us/step - acc: 0.9844 - loss: 0.0479

33264/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 451us/step - acc: 0.9844 - loss: 0.0479

33378/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 451us/step - acc: 0.9844 - loss: 0.0479

33470/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 451us/step - acc: 0.9844 - loss: 0.0479

33570/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 451us/step - acc: 0.9844 - loss: 0.0479

33666/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 452us/step - acc: 0.9844 - loss: 0.0479

33756/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 452us/step - acc: 0.9844 - loss: 0.0479

33851/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 452us/step - acc: 0.9844 - loss: 0.0479

33946/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 452us/step - acc: 0.9844 - loss: 0.0479

34029/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 453us/step - acc: 0.9844 - loss: 0.0479

34130/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 453us/step - acc: 0.9844 - loss: 0.0479

34250/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 453us/step - acc: 0.9844 - loss: 0.0479

34352/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 453us/step - acc: 0.9844 - loss: 0.0479

34447/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 453us/step - acc: 0.9844 - loss: 0.0479

34560/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 453us/step - acc: 0.9844 - loss: 0.0479

34670/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 453us/step - acc: 0.9844 - loss: 0.0478

34792/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 453us/step - acc: 0.9844 - loss: 0.0478

34905/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 453us/step - acc: 0.9844 - loss: 0.0478

35010/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 453us/step - acc: 0.9844 - loss: 0.0478

35068/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 454us/step - acc: 0.9844 - loss: 0.0478

35138/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 454us/step - acc: 0.9844 - loss: 0.0478

35221/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 454us/step - acc: 0.9844 - loss: 0.0478

35307/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 455us/step - acc: 0.9844 - loss: 0.0478

35400/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 455us/step - acc: 0.9844 - loss: 0.0478

35507/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 455us/step - acc: 0.9844 - loss: 0.0478

35616/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 455us/step - acc: 0.9844 - loss: 0.0478

35723/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 455us/step - acc: 0.9844 - loss: 0.0478

35847/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 455us/step - acc: 0.9844 - loss: 0.0478

35947/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 455us/step - acc: 0.9844 - loss: 0.0478

35989/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 456us/step - acc: 0.9844 - loss: 0.0478

36069/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 456us/step - acc: 0.9844 - loss: 0.0478

36141/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 457us/step - acc: 0.9844 - loss: 0.0478

36259/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 457us/step - acc: 0.9844 - loss: 0.0478

36349/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 457us/step - acc: 0.9844 - loss: 0.0478

36465/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 457us/step - acc: 0.9844 - loss: 0.0478

36578/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 457us/step - acc: 0.9844 - loss: 0.0478

36674/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 457us/step - acc: 0.9844 - loss: 0.0478

36760/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 457us/step - acc: 0.9844 - loss: 0.0478

36855/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 458us/step - acc: 0.9844 - loss: 0.0478

36958/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 458us/step - acc: 0.9844 - loss: 0.0478

37057/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 458us/step - acc: 0.9844 - loss: 0.0478

37174/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 458us/step - acc: 0.9844 - loss: 0.0478

37289/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 458us/step - acc: 0.9844 - loss: 0.0478

37400/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 458us/step - acc: 0.9844 - loss: 0.0478

37503/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 458us/step - acc: 0.9844 - loss: 0.0478

37544/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 458us/step - acc: 0.9844 - loss: 0.0478

37588/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 459us/step - acc: 0.9844 - loss: 0.0478

37683/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 459us/step - acc: 0.9844 - loss: 0.0478

37783/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 460us/step - acc: 0.9844 - loss: 0.0478

37877/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 460us/step - acc: 0.9844 - loss: 0.0478

37945/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 460us/step - acc: 0.9844 - loss: 0.0478

38054/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 460us/step - acc: 0.9844 - loss: 0.0478

38167/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 460us/step - acc: 0.9844 - loss: 0.0478

38280/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 460us/step - acc: 0.9844 - loss: 0.0478 

38399/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 460us/step - acc: 0.9844 - loss: 0.0478

38516/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 460us/step - acc: 0.9844 - loss: 0.0478

38608/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 460us/step - acc: 0.9844 - loss: 0.0478

38706/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 460us/step - acc: 0.9844 - loss: 0.0478

38822/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 460us/step - acc: 0.9844 - loss: 0.0478

38913/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 460us/step - acc: 0.9844 - loss: 0.0478

38994/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 461us/step - acc: 0.9844 - loss: 0.0478

39079/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 461us/step - acc: 0.9844 - loss: 0.0478

39187/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 461us/step - acc: 0.9844 - loss: 0.0478

39292/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 461us/step - acc: 0.9844 - loss: 0.0478

39391/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 461us/step - acc: 0.9844 - loss: 0.0478

39502/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 461us/step - acc: 0.9844 - loss: 0.0478

39608/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 461us/step - acc: 0.9844 - loss: 0.0478

39716/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 461us/step - acc: 0.9844 - loss: 0.0478

39817/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 461us/step - acc: 0.9844 - loss: 0.0478

39935/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 461us/step - acc: 0.9844 - loss: 0.0478

40047/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 461us/step - acc: 0.9844 - loss: 0.0478

40152/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 461us/step - acc: 0.9844 - loss: 0.0478

40270/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 461us/step - acc: 0.9844 - loss: 0.0478

40384/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 461us/step - acc: 0.9844 - loss: 0.0478

40472/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 461us/step - acc: 0.9844 - loss: 0.0478

40548/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 462us/step - acc: 0.9844 - loss: 0.0478

40639/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 462us/step - acc: 0.9844 - loss: 0.0478

40744/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 462us/step - acc: 0.9844 - loss: 0.0478

40849/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 462us/step - acc: 0.9844 - loss: 0.0478

40893/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 463us/step - acc: 0.9844 - loss: 0.0478

40938/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 463us/step - acc: 0.9844 - loss: 0.0478

40985/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 464us/step - acc: 0.9844 - loss: 0.0478

41031/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 465us/step - acc: 0.9844 - loss: 0.0478

41058/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 466us/step - acc: 0.9844 - loss: 0.0478

41074/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 467us/step - acc: 0.9844 - loss: 0.0478

41079/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 468us/step - acc: 0.9844 - loss: 0.0478

41089/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 469us/step - acc: 0.9844 - loss: 0.0478

41132/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 470us/step - acc: 0.9844 - loss: 0.0478

41166/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 471us/step - acc: 0.9844 - loss: 0.0478

41280/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 471us/step - acc: 0.9844 - loss: 0.0478

41392/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 471us/step - acc: 0.9844 - loss: 0.0478

41521/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 471us/step - acc: 0.9844 - loss: 0.0478

41655/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 470us/step - acc: 0.9844 - loss: 0.0478

41775/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 470us/step - acc: 0.9844 - loss: 0.0478

41900/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 470us/step - acc: 0.9844 - loss: 0.0478

42028/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 470us/step - acc: 0.9844 - loss: 0.0478

42164/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 469us/step - acc: 0.9844 - loss: 0.0478

42283/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 469us/step - acc: 0.9844 - loss: 0.0478

42390/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 469us/step - acc: 0.9844 - loss: 0.0478

42491/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 469us/step - acc: 0.9844 - loss: 0.0478

42609/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 469us/step - acc: 0.9844 - loss: 0.0478

42729/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 469us/step - acc: 0.9844 - loss: 0.0478

42849/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 469us/step - acc: 0.9844 - loss: 0.0478

42970/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 469us/step - acc: 0.9844 - loss: 0.0478

43084/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 469us/step - acc: 0.9845 - loss: 0.0478

43212/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 468us/step - acc: 0.9845 - loss: 0.0478

43339/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 468us/step - acc: 0.9845 - loss: 0.0478

43455/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 468us/step - acc: 0.9845 - loss: 0.0478

43574/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 468us/step - acc: 0.9845 - loss: 0.0478

43692/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 468us/step - acc: 0.9845 - loss: 0.0478

43814/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 468us/step - acc: 0.9845 - loss: 0.0478

43940/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 468us/step - acc: 0.9845 - loss: 0.0478

44064/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 467us/step - acc: 0.9845 - loss: 0.0478

44179/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 467us/step - acc: 0.9845 - loss: 0.0478

44307/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 467us/step - acc: 0.9845 - loss: 0.0478

44430/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 467us/step - acc: 0.9845 - loss: 0.0478

44558/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 467us/step - acc: 0.9845 - loss: 0.0478

44680/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 467us/step - acc: 0.9845 - loss: 0.0478

44805/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 466us/step - acc: 0.9845 - loss: 0.0478

44920/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 466us/step - acc: 0.9845 - loss: 0.0478

45035/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 466us/step - acc: 0.9845 - loss: 0.0478

45142/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 466us/step - acc: 0.9845 - loss: 0.0478

45252/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 466us/step - acc: 0.9845 - loss: 0.0478

45363/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 466us/step - acc: 0.9845 - loss: 0.0478

45483/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 466us/step - acc: 0.9845 - loss: 0.0478

45609/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 466us/step - acc: 0.9845 - loss: 0.0478

45735/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 466us/step - acc: 0.9845 - loss: 0.0478

45860/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 466us/step - acc: 0.9845 - loss: 0.0478

45971/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 465us/step - acc: 0.9845 - loss: 0.0478

46085/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 465us/step - acc: 0.9845 - loss: 0.0478

46208/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 465us/step - acc: 0.9845 - loss: 0.0478

46326/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 465us/step - acc: 0.9845 - loss: 0.0478

46452/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 465us/step - acc: 0.9845 - loss: 0.0478

46574/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 465us/step - acc: 0.9845 - loss: 0.0478

46699/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 465us/step - acc: 0.9845 - loss: 0.0478

46809/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 465us/step - acc: 0.9845 - loss: 0.0478

46940/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 464us/step - acc: 0.9845 - loss: 0.0478

47064/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 464us/step - acc: 0.9845 - loss: 0.0478

47196/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 464us/step - acc: 0.9845 - loss: 0.0478

47317/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 464us/step - acc: 0.9845 - loss: 0.0478

47426/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 464us/step - acc: 0.9845 - loss: 0.0478

47541/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 464us/step - acc: 0.9845 - loss: 0.0478

47653/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 464us/step - acc: 0.9845 - loss: 0.0478

47760/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 464us/step - acc: 0.9845 - loss: 0.0478

47863/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 464us/step - acc: 0.9845 - loss: 0.0478

47972/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 464us/step - acc: 0.9845 - loss: 0.0478

48066/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 464us/step - acc: 0.9845 - loss: 0.0478

48168/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 464us/step - acc: 0.9845 - loss: 0.0478

48281/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 464us/step - acc: 0.9845 - loss: 0.0478

48372/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 464us/step - acc: 0.9845 - loss: 0.0478

48478/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 464us/step - acc: 0.9845 - loss: 0.0478

48593/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 464us/step - acc: 0.9845 - loss: 0.0478

48689/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 464us/step - acc: 0.9845 - loss: 0.0478

48772/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 465us/step - acc: 0.9845 - loss: 0.0478

48850/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 465us/step - acc: 0.9845 - loss: 0.0478

48937/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 465us/step - acc: 0.9845 - loss: 0.0478

49027/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 465us/step - acc: 0.9845 - loss: 0.0478

49148/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 465us/step - acc: 0.9845 - loss: 0.0478

49234/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 465us/step - acc: 0.9845 - loss: 0.0478

49327/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 465us/step - acc: 0.9845 - loss: 0.0478

49396/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 466us/step - acc: 0.9845 - loss: 0.0478

49499/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 466us/step - acc: 0.9845 - loss: 0.0478

49618/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 466us/step - acc: 0.9845 - loss: 0.0478

49734/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 466us/step - acc: 0.9845 - loss: 0.0478

49849/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 466us/step - acc: 0.9845 - loss: 0.0478

49976/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 465us/step - acc: 0.9845 - loss: 0.0478

50091/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 465us/step - acc: 0.9845 - loss: 0.0478

50180/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 466us/step - acc: 0.9845 - loss: 0.0478

50275/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 466us/step - acc: 0.9845 - loss: 0.0478

50391/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 466us/step - acc: 0.9845 - loss: 0.0478

50502/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 466us/step - acc: 0.9845 - loss: 0.0478

50622/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 465us/step - acc: 0.9845 - loss: 0.0478

50685/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 466us/step - acc: 0.9845 - loss: 0.0478

50755/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 466us/step - acc: 0.9845 - loss: 0.0478

50871/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 466us/step - acc: 0.9845 - loss: 0.0478

50983/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 466us/step - acc: 0.9845 - loss: 0.0478

51105/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 466us/step - acc: 0.9845 - loss: 0.0478

51224/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 466us/step - acc: 0.9845 - loss: 0.0478

51346/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 466us/step - acc: 0.9845 - loss: 0.0478

51463/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0478

51551/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0478

51632/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0478

51725/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0478

51822/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0478

51932/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0478

52055/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0478

52170/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0478

52288/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0478

52393/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0478

52483/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0478

52595/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0478

52712/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0478

52826/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0478

52945/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0477

53063/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0477

53184/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0477

53306/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0477

53419/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0477

53544/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 466us/step - acc: 0.9845 - loss: 0.0477

53670/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 465us/step - acc: 0.9845 - loss: 0.0477

53793/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 465us/step - acc: 0.9845 - loss: 0.0477

53890/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 465us/step - acc: 0.9845 - loss: 0.0477

54009/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 465us/step - acc: 0.9845 - loss: 0.0477

54130/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 465us/step - acc: 0.9845 - loss: 0.0477

54247/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 465us/step - acc: 0.9845 - loss: 0.0477

54368/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 465us/step - acc: 0.9845 - loss: 0.0477

54492/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 465us/step - acc: 0.9845 - loss: 0.0477

54617/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 465us/step - acc: 0.9845 - loss: 0.0477

54738/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 465us/step - acc: 0.9845 - loss: 0.0477

54841/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 465us/step - acc: 0.9845 - loss: 0.0478

54934/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 465us/step - acc: 0.9845 - loss: 0.0478

55032/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 465us/step - acc: 0.9845 - loss: 0.0478

55138/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 465us/step - acc: 0.9845 - loss: 0.0478

55264/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 465us/step - acc: 0.9845 - loss: 0.0478

55399/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 464us/step - acc: 0.9845 - loss: 0.0478

55537/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 464us/step - acc: 0.9845 - loss: 0.0478

55675/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 464us/step - acc: 0.9845 - loss: 0.0478

55813/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 464us/step - acc: 0.9845 - loss: 0.0478

55937/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 464us/step - acc: 0.9845 - loss: 0.0478

56072/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 463us/step - acc: 0.9845 - loss: 0.0478

56210/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 463us/step - acc: 0.9845 - loss: 0.0478

56348/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 463us/step - acc: 0.9845 - loss: 0.0478

56486/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 463us/step - acc: 0.9845 - loss: 0.0478

56621/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 462us/step - acc: 0.9845 - loss: 0.0478

56747/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 462us/step - acc: 0.9845 - loss: 0.0478

56874/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 462us/step - acc: 0.9845 - loss: 0.0478

56999/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 462us/step - acc: 0.9844 - loss: 0.0478

57123/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 462us/step - acc: 0.9844 - loss: 0.0478

57250/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 462us/step - acc: 0.9844 - loss: 0.0478

57382/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 462us/step - acc: 0.9844 - loss: 0.0478

57519/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 461us/step - acc: 0.9844 - loss: 0.0478

57657/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 461us/step - acc: 0.9844 - loss: 0.0478

57793/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 461us/step - acc: 0.9844 - loss: 0.0478

57931/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 461us/step - acc: 0.9844 - loss: 0.0478

58067/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 460us/step - acc: 0.9844 - loss: 0.0478

58205/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 460us/step - acc: 0.9844 - loss: 0.0478

58343/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 460us/step - acc: 0.9844 - loss: 0.0478

58480/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 460us/step - acc: 0.9844 - loss: 0.0478

58615/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 460us/step - acc: 0.9844 - loss: 0.0478

58751/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 459us/step - acc: 0.9844 - loss: 0.0478

58887/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 459us/step - acc: 0.9844 - loss: 0.0478

59021/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 459us/step - acc: 0.9844 - loss: 0.0478

59158/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 459us/step - acc: 0.9844 - loss: 0.0478

59291/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 459us/step - acc: 0.9844 - loss: 0.0478

59430/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 458us/step - acc: 0.9844 - loss: 0.0478

59555/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 458us/step - acc: 0.9844 - loss: 0.0478

59679/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 458us/step - acc: 0.9844 - loss: 0.0478

59813/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 458us/step - acc: 0.9844 - loss: 0.0478

59950/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 458us/step - acc: 0.9844 - loss: 0.0478

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 517us/step - acc: 0.9844 - loss: 0.0478 - val_acc: 0.9692 - val_loss: 0.1108

Epoch 11/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 10:25 10ms/step - acc: 1.0000 - loss: 9.5775e-04

  120/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 422us/step - acc: 0.9987 - loss: 0.0167     

  242/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 418us/step - acc: 0.9945 - loss: 0.0258

  360/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 420us/step - acc: 0.9934 - loss: 0.0275

  481/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 419us/step - acc: 0.9932 - loss: 0.0274

  603/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 418us/step - acc: 0.9935 - loss: 0.0264

  727/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 416us/step - acc: 0.9937 - loss: 0.0254

  863/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 408us/step - acc: 0.9938 - loss: 0.0247

  993/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 405us/step - acc: 0.9937 - loss: 0.0244

 1119/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 405us/step - acc: 0.9935 - loss: 0.0243

 1252/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 402us/step - acc: 0.9931 - loss: 0.0247

 1387/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 399us/step - acc: 0.9926 - loss: 0.0257

 1534/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 393us/step - acc: 0.9920 - loss: 0.0269

 1673/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 391us/step - acc: 0.9916 - loss: 0.0280

 1807/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 389us/step - acc: 0.9913 - loss: 0.0288

 1948/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 387us/step - acc: 0.9911 - loss: 0.0296

 2081/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 386us/step - acc: 0.9908 - loss: 0.0304

 2212/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 386us/step - acc: 0.9905 - loss: 0.0311

 2341/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 386us/step - acc: 0.9903 - loss: 0.0320

 2470/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 386us/step - acc: 0.9900 - loss: 0.0329

 2603/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 386us/step - acc: 0.9898 - loss: 0.0337

 2728/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 387us/step - acc: 0.9896 - loss: 0.0342

 2854/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 387us/step - acc: 0.9895 - loss: 0.0347

 2989/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 386us/step - acc: 0.9894 - loss: 0.0352

 3124/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 386us/step - acc: 0.9893 - loss: 0.0355

 3256/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 386us/step - acc: 0.9892 - loss: 0.0358

 3378/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 387us/step - acc: 0.9891 - loss: 0.0360

 3498/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 388us/step - acc: 0.9891 - loss: 0.0361

 3626/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 388us/step - acc: 0.9890 - loss: 0.0363

 3751/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 388us/step - acc: 0.9890 - loss: 0.0364

 3875/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 389us/step - acc: 0.9890 - loss: 0.0364

 4002/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 389us/step - acc: 0.9890 - loss: 0.0365

 4137/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 388us/step - acc: 0.9890 - loss: 0.0365

 4274/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 388us/step - acc: 0.9890 - loss: 0.0365

 4415/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 387us/step - acc: 0.9890 - loss: 0.0365

 4554/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 386us/step - acc: 0.9890 - loss: 0.0365

 4691/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 385us/step - acc: 0.9890 - loss: 0.0365

 4827/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 385us/step - acc: 0.9890 - loss: 0.0365

 4955/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 385us/step - acc: 0.9890 - loss: 0.0365

 5089/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 385us/step - acc: 0.9890 - loss: 0.0364

 5202/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 386us/step - acc: 0.9890 - loss: 0.0364

 5332/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 386us/step - acc: 0.9890 - loss: 0.0364

 5469/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 386us/step - acc: 0.9890 - loss: 0.0364

 5606/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 385us/step - acc: 0.9890 - loss: 0.0364

 5742/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 385us/step - acc: 0.9890 - loss: 0.0364

 5880/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 384us/step - acc: 0.9890 - loss: 0.0363

 6009/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 384us/step - acc: 0.9891 - loss: 0.0363

 6147/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 384us/step - acc: 0.9891 - loss: 0.0363

 6280/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 384us/step - acc: 0.9891 - loss: 0.0363

 6419/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 383us/step - acc: 0.9891 - loss: 0.0363

 6556/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 383us/step - acc: 0.9891 - loss: 0.0363

 6681/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 383us/step - acc: 0.9891 - loss: 0.0363

 6813/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 383us/step - acc: 0.9891 - loss: 0.0362

 6941/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 383us/step - acc: 0.9891 - loss: 0.0362

 7081/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 383us/step - acc: 0.9891 - loss: 0.0362

 7218/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 383us/step - acc: 0.9891 - loss: 0.0362

 7356/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 382us/step - acc: 0.9892 - loss: 0.0362

 7497/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 382us/step - acc: 0.9892 - loss: 0.0362

 7626/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 382us/step - acc: 0.9892 - loss: 0.0362

 7757/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 382us/step - acc: 0.9892 - loss: 0.0361

 7890/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 382us/step - acc: 0.9892 - loss: 0.0361

 8027/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 382us/step - acc: 0.9892 - loss: 0.0361

 8163/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 381us/step - acc: 0.9892 - loss: 0.0361

 8298/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 381us/step - acc: 0.9892 - loss: 0.0361

 8435/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 381us/step - acc: 0.9892 - loss: 0.0361

 8573/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 381us/step - acc: 0.9892 - loss: 0.0361

 8708/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 380us/step - acc: 0.9892 - loss: 0.0360

 8844/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 380us/step - acc: 0.9892 - loss: 0.0360

 8977/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 380us/step - acc: 0.9892 - loss: 0.0360

 9114/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 380us/step - acc: 0.9892 - loss: 0.0360

 9250/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 380us/step - acc: 0.9892 - loss: 0.0359

 9386/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 380us/step - acc: 0.9892 - loss: 0.0359

 9515/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 380us/step - acc: 0.9892 - loss: 0.0359

 9651/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 380us/step - acc: 0.9892 - loss: 0.0359

 9775/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 380us/step - acc: 0.9892 - loss: 0.0359

 9895/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 381us/step - acc: 0.9892 - loss: 0.0359

10021/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 381us/step - acc: 0.9892 - loss: 0.0359

10147/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 381us/step - acc: 0.9892 - loss: 0.0359

10276/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 381us/step - acc: 0.9892 - loss: 0.0359

10411/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 381us/step - acc: 0.9892 - loss: 0.0359

10549/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 381us/step - acc: 0.9892 - loss: 0.0359

10684/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 381us/step - acc: 0.9892 - loss: 0.0359

10823/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 380us/step - acc: 0.9892 - loss: 0.0359

10960/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 380us/step - acc: 0.9892 - loss: 0.0359

11098/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 380us/step - acc: 0.9892 - loss: 0.0359

11235/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 380us/step - acc: 0.9892 - loss: 0.0359

11371/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 380us/step - acc: 0.9892 - loss: 0.0359

11510/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 379us/step - acc: 0.9892 - loss: 0.0359

11646/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 379us/step - acc: 0.9892 - loss: 0.0359

11781/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 379us/step - acc: 0.9892 - loss: 0.0360

11920/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 379us/step - acc: 0.9891 - loss: 0.0360

12057/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 379us/step - acc: 0.9891 - loss: 0.0360

12196/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 379us/step - acc: 0.9891 - loss: 0.0360

12334/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 379us/step - acc: 0.9891 - loss: 0.0361

12470/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 378us/step - acc: 0.9891 - loss: 0.0361

12606/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 378us/step - acc: 0.9891 - loss: 0.0361

12734/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 378us/step - acc: 0.9891 - loss: 0.0361

12867/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 378us/step - acc: 0.9891 - loss: 0.0362

13005/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 378us/step - acc: 0.9891 - loss: 0.0362

13140/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 378us/step - acc: 0.9890 - loss: 0.0362

13277/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 378us/step - acc: 0.9890 - loss: 0.0363

13412/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 378us/step - acc: 0.9890 - loss: 0.0363

13548/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 378us/step - acc: 0.9890 - loss: 0.0363

13686/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 378us/step - acc: 0.9890 - loss: 0.0363

13824/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 378us/step - acc: 0.9890 - loss: 0.0364

13963/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9890 - loss: 0.0364

14102/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9890 - loss: 0.0364

14236/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9889 - loss: 0.0365

14370/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9889 - loss: 0.0365

14505/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9889 - loss: 0.0366

14640/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9889 - loss: 0.0366

14777/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 377us/step - acc: 0.9889 - loss: 0.0366

14915/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 377us/step - acc: 0.9889 - loss: 0.0367

15053/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 377us/step - acc: 0.9889 - loss: 0.0367

15190/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 377us/step - acc: 0.9888 - loss: 0.0368

15327/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 377us/step - acc: 0.9888 - loss: 0.0368

15460/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 377us/step - acc: 0.9888 - loss: 0.0369

15598/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9888 - loss: 0.0369

15735/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9888 - loss: 0.0369

15873/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9888 - loss: 0.0370

16012/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9888 - loss: 0.0370

16147/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9887 - loss: 0.0370

16280/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9887 - loss: 0.0371

16406/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9887 - loss: 0.0371

16532/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9887 - loss: 0.0372

16657/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 377us/step - acc: 0.9887 - loss: 0.0372

16781/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 377us/step - acc: 0.9887 - loss: 0.0372

16899/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 377us/step - acc: 0.9887 - loss: 0.0373

17032/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 377us/step - acc: 0.9887 - loss: 0.0373

17168/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 377us/step - acc: 0.9886 - loss: 0.0373

17305/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 377us/step - acc: 0.9886 - loss: 0.0374

17440/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 377us/step - acc: 0.9886 - loss: 0.0374

17576/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 377us/step - acc: 0.9886 - loss: 0.0374

17715/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 377us/step - acc: 0.9886 - loss: 0.0375

17852/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 377us/step - acc: 0.9886 - loss: 0.0375

17991/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 377us/step - acc: 0.9886 - loss: 0.0375

18122/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 377us/step - acc: 0.9886 - loss: 0.0375

18259/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 377us/step - acc: 0.9886 - loss: 0.0376

18393/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 377us/step - acc: 0.9885 - loss: 0.0376

18528/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 377us/step - acc: 0.9885 - loss: 0.0376

18664/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9885 - loss: 0.0377

18800/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9885 - loss: 0.0377

18935/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9885 - loss: 0.0377

19068/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9885 - loss: 0.0378

19205/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9885 - loss: 0.0378

19341/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9885 - loss: 0.0378

19477/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9885 - loss: 0.0378

19616/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9885 - loss: 0.0379

19753/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9884 - loss: 0.0379

19893/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9884 - loss: 0.0379

20030/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 376us/step - acc: 0.9884 - loss: 0.0380

20165/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 376us/step - acc: 0.9884 - loss: 0.0380

20300/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 376us/step - acc: 0.9884 - loss: 0.0380

20442/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 376us/step - acc: 0.9884 - loss: 0.0380

20582/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 376us/step - acc: 0.9884 - loss: 0.0381

20719/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 375us/step - acc: 0.9884 - loss: 0.0381

20852/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 375us/step - acc: 0.9884 - loss: 0.0381

20989/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 375us/step - acc: 0.9884 - loss: 0.0381

21126/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 375us/step - acc: 0.9884 - loss: 0.0382

21260/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 375us/step - acc: 0.9883 - loss: 0.0382

21398/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 375us/step - acc: 0.9883 - loss: 0.0382

21534/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 375us/step - acc: 0.9883 - loss: 0.0382

21672/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 375us/step - acc: 0.9883 - loss: 0.0382

21809/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 375us/step - acc: 0.9883 - loss: 0.0383

21948/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 375us/step - acc: 0.9883 - loss: 0.0383

22086/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 375us/step - acc: 0.9883 - loss: 0.0383

22224/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 375us/step - acc: 0.9883 - loss: 0.0383

22360/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 375us/step - acc: 0.9883 - loss: 0.0383

22501/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 375us/step - acc: 0.9883 - loss: 0.0384

22639/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9883 - loss: 0.0384

22779/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9882 - loss: 0.0384

22915/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9882 - loss: 0.0384

23047/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9882 - loss: 0.0384

23182/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9882 - loss: 0.0384

23319/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9882 - loss: 0.0385

23451/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9882 - loss: 0.0385

23573/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9882 - loss: 0.0385

23702/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9882 - loss: 0.0385

23830/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9882 - loss: 0.0385

23966/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9882 - loss: 0.0385

24091/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9882 - loss: 0.0385

24220/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9882 - loss: 0.0386

24351/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9882 - loss: 0.0386

24490/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9882 - loss: 0.0386

24622/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9881 - loss: 0.0386

24760/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9881 - loss: 0.0386

24895/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9881 - loss: 0.0386

25036/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9881 - loss: 0.0387

25176/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 375us/step - acc: 0.9881 - loss: 0.0387

25315/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 375us/step - acc: 0.9881 - loss: 0.0387

25454/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 375us/step - acc: 0.9881 - loss: 0.0387

25575/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 375us/step - acc: 0.9881 - loss: 0.0387

25705/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 375us/step - acc: 0.9881 - loss: 0.0387

25841/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 375us/step - acc: 0.9881 - loss: 0.0387

25979/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 375us/step - acc: 0.9881 - loss: 0.0387

26119/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 375us/step - acc: 0.9881 - loss: 0.0387

26258/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 375us/step - acc: 0.9881 - loss: 0.0388

26395/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 375us/step - acc: 0.9881 - loss: 0.0388

26517/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 375us/step - acc: 0.9881 - loss: 0.0388

26651/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 375us/step - acc: 0.9881 - loss: 0.0388

26788/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 375us/step - acc: 0.9880 - loss: 0.0388

26925/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 375us/step - acc: 0.9880 - loss: 0.0388

27062/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 375us/step - acc: 0.9880 - loss: 0.0388

27201/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 375us/step - acc: 0.9880 - loss: 0.0388

27338/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 375us/step - acc: 0.9880 - loss: 0.0388

27476/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 374us/step - acc: 0.9880 - loss: 0.0388

27611/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 374us/step - acc: 0.9880 - loss: 0.0389

27750/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 374us/step - acc: 0.9880 - loss: 0.0389

27890/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 374us/step - acc: 0.9880 - loss: 0.0389

28028/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 374us/step - acc: 0.9880 - loss: 0.0389

28156/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 374us/step - acc: 0.9880 - loss: 0.0389

28293/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 374us/step - acc: 0.9880 - loss: 0.0389

28429/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 374us/step - acc: 0.9880 - loss: 0.0389

28562/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 374us/step - acc: 0.9880 - loss: 0.0389

28683/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 374us/step - acc: 0.9880 - loss: 0.0389

28803/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 375us/step - acc: 0.9880 - loss: 0.0389

28941/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 375us/step - acc: 0.9880 - loss: 0.0389

29080/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 375us/step - acc: 0.9880 - loss: 0.0389

29217/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 374us/step - acc: 0.9880 - loss: 0.0389

29356/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 374us/step - acc: 0.9880 - loss: 0.0390

29498/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 374us/step - acc: 0.9880 - loss: 0.0390

29636/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 374us/step - acc: 0.9880 - loss: 0.0390

29774/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 374us/step - acc: 0.9879 - loss: 0.0390

29912/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 374us/step - acc: 0.9879 - loss: 0.0390

30048/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 374us/step - acc: 0.9879 - loss: 0.0390

30187/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 374us/step - acc: 0.9879 - loss: 0.0390

30324/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 374us/step - acc: 0.9879 - loss: 0.0390

30450/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 374us/step - acc: 0.9879 - loss: 0.0390

30589/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 374us/step - acc: 0.9879 - loss: 0.0390

30726/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 374us/step - acc: 0.9879 - loss: 0.0390

30865/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 374us/step - acc: 0.9879 - loss: 0.0390

31005/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 374us/step - acc: 0.9879 - loss: 0.0390

31141/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 374us/step - acc: 0.9879 - loss: 0.0391

31279/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 374us/step - acc: 0.9879 - loss: 0.0391

31416/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 374us/step - acc: 0.9879 - loss: 0.0391

31550/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 374us/step - acc: 0.9879 - loss: 0.0391

31687/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 374us/step - acc: 0.9879 - loss: 0.0391

31822/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 374us/step - acc: 0.9879 - loss: 0.0391

31959/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 374us/step - acc: 0.9879 - loss: 0.0391

32096/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 374us/step - acc: 0.9879 - loss: 0.0391

32224/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 374us/step - acc: 0.9879 - loss: 0.0391

32361/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 374us/step - acc: 0.9879 - loss: 0.0391

32498/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 374us/step - acc: 0.9878 - loss: 0.0392

32636/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 374us/step - acc: 0.9878 - loss: 0.0392

32772/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 374us/step - acc: 0.9878 - loss: 0.0392

32909/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 374us/step - acc: 0.9878 - loss: 0.0392

33041/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 374us/step - acc: 0.9878 - loss: 0.0392

33179/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 374us/step - acc: 0.9878 - loss: 0.0392

33318/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 374us/step - acc: 0.9878 - loss: 0.0392 

33456/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 374us/step - acc: 0.9878 - loss: 0.0392

33590/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 374us/step - acc: 0.9878 - loss: 0.0392

33726/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 374us/step - acc: 0.9878 - loss: 0.0392

33862/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9878 - loss: 0.0392

34000/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9878 - loss: 0.0393

34137/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9878 - loss: 0.0393

34266/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9878 - loss: 0.0393

34403/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9878 - loss: 0.0393

34527/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 374us/step - acc: 0.9878 - loss: 0.0393

34663/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 374us/step - acc: 0.9878 - loss: 0.0393

34799/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 374us/step - acc: 0.9878 - loss: 0.0393

34936/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 374us/step - acc: 0.9878 - loss: 0.0393

35072/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9878 - loss: 0.0393

35209/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9878 - loss: 0.0393

35347/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9878 - loss: 0.0393

35484/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9878 - loss: 0.0393

35619/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9878 - loss: 0.0394

35758/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9877 - loss: 0.0394

35897/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0394

36026/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0394

36163/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0394

36305/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0394

36436/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0394

36570/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0394

36709/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0394

36836/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0394

36963/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0394

37097/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0394

37235/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0394

37372/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0394

37510/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0394

37648/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0394

37786/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0395

37922/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0395

38059/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0395

38195/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0395

38322/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0395

38459/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9877 - loss: 0.0395

38596/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9877 - loss: 0.0395

38734/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9877 - loss: 0.0395

38869/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9877 - loss: 0.0395

39008/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9877 - loss: 0.0395

39148/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9877 - loss: 0.0395

39286/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9877 - loss: 0.0395

39425/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9877 - loss: 0.0395

39562/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9877 - loss: 0.0395

39696/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9877 - loss: 0.0395

39834/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9877 - loss: 0.0395

39972/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9877 - loss: 0.0395

40110/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9877 - loss: 0.0396

40249/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9877 - loss: 0.0396

40387/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9877 - loss: 0.0396

40527/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9876 - loss: 0.0396

40665/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9876 - loss: 0.0396

40801/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9876 - loss: 0.0396

40936/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9876 - loss: 0.0396

41072/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9876 - loss: 0.0396

41207/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9876 - loss: 0.0396

41345/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9876 - loss: 0.0396

41484/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9876 - loss: 0.0396

41624/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9876 - loss: 0.0396

41757/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9876 - loss: 0.0396

41883/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9876 - loss: 0.0396

42007/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9876 - loss: 0.0396

42136/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9876 - loss: 0.0397

42273/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9876 - loss: 0.0397

42409/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9876 - loss: 0.0397

42550/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9876 - loss: 0.0397

42686/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9876 - loss: 0.0397

42823/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9876 - loss: 0.0397

42961/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9876 - loss: 0.0397

43099/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9876 - loss: 0.0397

43237/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9876 - loss: 0.0397

43372/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9876 - loss: 0.0397

43504/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9876 - loss: 0.0397

43637/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9876 - loss: 0.0397

43774/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9876 - loss: 0.0398

43912/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9876 - loss: 0.0398

44045/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9876 - loss: 0.0398

44182/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9876 - loss: 0.0398

44321/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9876 - loss: 0.0398

44454/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9876 - loss: 0.0398

44580/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9876 - loss: 0.0398

44708/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9876 - loss: 0.0398

44831/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9876 - loss: 0.0398

44962/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9875 - loss: 0.0398

45091/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9875 - loss: 0.0398

45229/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9875 - loss: 0.0398

45368/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9875 - loss: 0.0399

45509/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9875 - loss: 0.0399

45647/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9875 - loss: 0.0399

45786/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9875 - loss: 0.0399

45925/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9875 - loss: 0.0399

46065/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9875 - loss: 0.0399

46205/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9875 - loss: 0.0399

46345/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 372us/step - acc: 0.9875 - loss: 0.0399

46481/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 372us/step - acc: 0.9875 - loss: 0.0399

46618/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0399

46756/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0399

46893/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0399

47031/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0399

47163/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0400

47287/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0400

47423/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0400

47559/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0400

47697/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0400

47833/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0400

47972/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0400

48111/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0400

48252/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0400

48392/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0400

48531/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0400

48671/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0400

48808/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0400

48946/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0400

49085/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0401

49220/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 372us/step - acc: 0.9875 - loss: 0.0401

49357/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 372us/step - acc: 0.9875 - loss: 0.0401

49470/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 372us/step - acc: 0.9875 - loss: 0.0401

49582/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 372us/step - acc: 0.9874 - loss: 0.0401

49707/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 373us/step - acc: 0.9874 - loss: 0.0401

49826/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 373us/step - acc: 0.9874 - loss: 0.0401

49958/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 373us/step - acc: 0.9874 - loss: 0.0401

50086/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 373us/step - acc: 0.9874 - loss: 0.0401

50208/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 373us/step - acc: 0.9874 - loss: 0.0401

50337/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 373us/step - acc: 0.9874 - loss: 0.0401

50456/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 373us/step - acc: 0.9874 - loss: 0.0401

50576/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 373us/step - acc: 0.9874 - loss: 0.0401

50696/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 373us/step - acc: 0.9874 - loss: 0.0401

50817/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 373us/step - acc: 0.9874 - loss: 0.0401

50948/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 373us/step - acc: 0.9874 - loss: 0.0401

51070/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 373us/step - acc: 0.9874 - loss: 0.0401

51200/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 373us/step - acc: 0.9874 - loss: 0.0401

51322/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 374us/step - acc: 0.9874 - loss: 0.0401

51452/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 374us/step - acc: 0.9874 - loss: 0.0402

51570/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 374us/step - acc: 0.9874 - loss: 0.0402

51688/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 374us/step - acc: 0.9874 - loss: 0.0402

51804/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 374us/step - acc: 0.9874 - loss: 0.0402

51917/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 374us/step - acc: 0.9874 - loss: 0.0402

52035/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 374us/step - acc: 0.9874 - loss: 0.0402

52142/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 374us/step - acc: 0.9874 - loss: 0.0402

52257/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 375us/step - acc: 0.9874 - loss: 0.0402

52373/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 375us/step - acc: 0.9874 - loss: 0.0402

52485/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 375us/step - acc: 0.9874 - loss: 0.0402

52595/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 375us/step - acc: 0.9874 - loss: 0.0402

52694/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 375us/step - acc: 0.9874 - loss: 0.0402

52811/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 375us/step - acc: 0.9874 - loss: 0.0402

52935/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 375us/step - acc: 0.9874 - loss: 0.0402

53061/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 376us/step - acc: 0.9874 - loss: 0.0402

53177/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 376us/step - acc: 0.9874 - loss: 0.0402

53293/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 376us/step - acc: 0.9874 - loss: 0.0402

53413/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 376us/step - acc: 0.9874 - loss: 0.0402

53533/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 376us/step - acc: 0.9874 - loss: 0.0402

53655/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 376us/step - acc: 0.9874 - loss: 0.0402

53789/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 376us/step - acc: 0.9874 - loss: 0.0402

53916/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 376us/step - acc: 0.9874 - loss: 0.0402

54028/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 376us/step - acc: 0.9874 - loss: 0.0402

54140/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 376us/step - acc: 0.9874 - loss: 0.0402

54236/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 377us/step - acc: 0.9874 - loss: 0.0402

54341/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 377us/step - acc: 0.9874 - loss: 0.0403

54458/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 377us/step - acc: 0.9874 - loss: 0.0403

54564/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 377us/step - acc: 0.9874 - loss: 0.0403

54678/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 377us/step - acc: 0.9874 - loss: 0.0403

54796/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 377us/step - acc: 0.9874 - loss: 0.0403

54914/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 377us/step - acc: 0.9874 - loss: 0.0403

55028/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 378us/step - acc: 0.9874 - loss: 0.0403

55147/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 378us/step - acc: 0.9874 - loss: 0.0403

55267/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 378us/step - acc: 0.9874 - loss: 0.0403

55386/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 378us/step - acc: 0.9873 - loss: 0.0403

55493/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 378us/step - acc: 0.9873 - loss: 0.0403

55614/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 378us/step - acc: 0.9873 - loss: 0.0403

55737/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 378us/step - acc: 0.9873 - loss: 0.0403

55859/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 378us/step - acc: 0.9873 - loss: 0.0403

55984/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 378us/step - acc: 0.9873 - loss: 0.0403

56104/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 378us/step - acc: 0.9873 - loss: 0.0403

56229/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 378us/step - acc: 0.9873 - loss: 0.0403

56341/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 379us/step - acc: 0.9873 - loss: 0.0403

56457/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 379us/step - acc: 0.9873 - loss: 0.0403

56575/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 379us/step - acc: 0.9873 - loss: 0.0404

56685/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 379us/step - acc: 0.9873 - loss: 0.0404

56803/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 379us/step - acc: 0.9873 - loss: 0.0404

56920/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 379us/step - acc: 0.9873 - loss: 0.0404

57030/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 379us/step - acc: 0.9873 - loss: 0.0404

57140/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 379us/step - acc: 0.9873 - loss: 0.0404

57254/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 380us/step - acc: 0.9873 - loss: 0.0404

57365/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 380us/step - acc: 0.9873 - loss: 0.0404

57464/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 380us/step - acc: 0.9873 - loss: 0.0404

57577/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 380us/step - acc: 0.9873 - loss: 0.0404

57692/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 380us/step - acc: 0.9873 - loss: 0.0404

57807/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 380us/step - acc: 0.9873 - loss: 0.0404

57924/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 380us/step - acc: 0.9873 - loss: 0.0404

58033/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9873 - loss: 0.0404

58145/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9873 - loss: 0.0404

58272/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9873 - loss: 0.0404

58389/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9873 - loss: 0.0404

58506/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9873 - loss: 0.0404

58618/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9873 - loss: 0.0404

58729/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9873 - loss: 0.0404

58846/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9873 - loss: 0.0404

58971/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9873 - loss: 0.0404

59067/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 382us/step - acc: 0.9873 - loss: 0.0405

59168/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 382us/step - acc: 0.9873 - loss: 0.0405

59272/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 382us/step - acc: 0.9873 - loss: 0.0405

59392/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 382us/step - acc: 0.9873 - loss: 0.0405

59510/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 382us/step - acc: 0.9873 - loss: 0.0405

59629/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 382us/step - acc: 0.9873 - loss: 0.0405

59717/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 382us/step - acc: 0.9873 - loss: 0.0405

59813/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 383us/step - acc: 0.9873 - loss: 0.0405

59932/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 383us/step - acc: 0.9873 - loss: 0.0405

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 443us/step - acc: 0.9873 - loss: 0.0405 - val_acc: 0.9717 - val_loss: 0.1089

Epoch 12/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 16:06 16ms/step - acc: 1.0000 - loss: 7.5102e-06

  117/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 434us/step - acc: 0.9788 - loss: 0.0681     

  238/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 425us/step - acc: 0.9778 - loss: 0.0802

  356/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 425us/step - acc: 0.9782 - loss: 0.0767

  475/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 424us/step - acc: 0.9783 - loss: 0.0735

  595/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 423us/step - acc: 0.9790 - loss: 0.0701

  720/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 419us/step - acc: 0.9798 - loss: 0.0672

  840/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 419us/step - acc: 0.9802 - loss: 0.0647

  961/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 419us/step - acc: 0.9805 - loss: 0.0627

 1080/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 419us/step - acc: 0.9808 - loss: 0.0614

 1199/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 420us/step - acc: 0.9810 - loss: 0.0604

 1311/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 422us/step - acc: 0.9813 - loss: 0.0595

 1418/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 426us/step - acc: 0.9815 - loss: 0.0586

 1523/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 429us/step - acc: 0.9817 - loss: 0.0577

 1633/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 431us/step - acc: 0.9819 - loss: 0.0568

 1750/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 431us/step - acc: 0.9822 - loss: 0.0558

 1867/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 431us/step - acc: 0.9825 - loss: 0.0549

 1981/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 432us/step - acc: 0.9827 - loss: 0.0542

 2093/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 433us/step - acc: 0.9829 - loss: 0.0535

 2196/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 435us/step - acc: 0.9831 - loss: 0.0529

 2314/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 435us/step - acc: 0.9832 - loss: 0.0522

 2431/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 434us/step - acc: 0.9834 - loss: 0.0517

 2547/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 434us/step - acc: 0.9835 - loss: 0.0512

 2664/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 434us/step - acc: 0.9835 - loss: 0.0508

 2774/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 435us/step - acc: 0.9836 - loss: 0.0504

 2889/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 435us/step - acc: 0.9837 - loss: 0.0499

 3006/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 435us/step - acc: 0.9838 - loss: 0.0494

 3118/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 435us/step - acc: 0.9839 - loss: 0.0490

 3242/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 434us/step - acc: 0.9840 - loss: 0.0486

 3365/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 433us/step - acc: 0.9841 - loss: 0.0483

 3477/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 434us/step - acc: 0.9842 - loss: 0.0480

 3601/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 433us/step - acc: 0.9843 - loss: 0.0477

 3708/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 434us/step - acc: 0.9844 - loss: 0.0474

 3816/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 435us/step - acc: 0.9844 - loss: 0.0472

 3930/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 435us/step - acc: 0.9845 - loss: 0.0469

 4048/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 434us/step - acc: 0.9846 - loss: 0.0465

 4150/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 436us/step - acc: 0.9847 - loss: 0.0463

 4271/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 435us/step - acc: 0.9848 - loss: 0.0460

 4394/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 435us/step - acc: 0.9849 - loss: 0.0456

 4502/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 435us/step - acc: 0.9850 - loss: 0.0454

 4620/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 435us/step - acc: 0.9851 - loss: 0.0451

 4738/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 435us/step - acc: 0.9852 - loss: 0.0448

 4851/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 435us/step - acc: 0.9853 - loss: 0.0445

 4970/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 435us/step - acc: 0.9853 - loss: 0.0443

 5088/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 435us/step - acc: 0.9854 - loss: 0.0440

 5192/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 436us/step - acc: 0.9855 - loss: 0.0438

 5310/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 435us/step - acc: 0.9855 - loss: 0.0436

 5421/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 436us/step - acc: 0.9856 - loss: 0.0434

 5525/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 437us/step - acc: 0.9857 - loss: 0.0432

 5644/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 436us/step - acc: 0.9857 - loss: 0.0430

 5767/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 436us/step - acc: 0.9858 - loss: 0.0428

 5891/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 435us/step - acc: 0.9859 - loss: 0.0426

 6021/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 434us/step - acc: 0.9859 - loss: 0.0424

 6147/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 433us/step - acc: 0.9860 - loss: 0.0422

 6261/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 433us/step - acc: 0.9860 - loss: 0.0421

 6364/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 434us/step - acc: 0.9861 - loss: 0.0419

 6478/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 434us/step - acc: 0.9861 - loss: 0.0418

 6592/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 435us/step - acc: 0.9862 - loss: 0.0416

 6713/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 434us/step - acc: 0.9862 - loss: 0.0415

 6822/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 435us/step - acc: 0.9863 - loss: 0.0414

 6937/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 435us/step - acc: 0.9863 - loss: 0.0412

 7067/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 434us/step - acc: 0.9863 - loss: 0.0411

 7185/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 434us/step - acc: 0.9864 - loss: 0.0410

 7312/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 433us/step - acc: 0.9864 - loss: 0.0408

 7426/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 433us/step - acc: 0.9865 - loss: 0.0407

 7547/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 433us/step - acc: 0.9865 - loss: 0.0406

 7686/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 432us/step - acc: 0.9865 - loss: 0.0405

 7823/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 430us/step - acc: 0.9866 - loss: 0.0403

 7943/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 430us/step - acc: 0.9866 - loss: 0.0402

 8076/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 429us/step - acc: 0.9866 - loss: 0.0401

 8212/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 428us/step - acc: 0.9867 - loss: 0.0400

 8345/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 427us/step - acc: 0.9867 - loss: 0.0399

 8483/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 426us/step - acc: 0.9867 - loss: 0.0397

 8612/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 426us/step - acc: 0.9868 - loss: 0.0396

 8744/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 425us/step - acc: 0.9868 - loss: 0.0395

 8878/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 424us/step - acc: 0.9868 - loss: 0.0394

 9013/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 424us/step - acc: 0.9869 - loss: 0.0393

 9151/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 423us/step - acc: 0.9869 - loss: 0.0392

 9287/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 422us/step - acc: 0.9869 - loss: 0.0391

 9420/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 421us/step - acc: 0.9870 - loss: 0.0390

 9557/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 421us/step - acc: 0.9870 - loss: 0.0390

 9696/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 420us/step - acc: 0.9870 - loss: 0.0389

 9831/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 419us/step - acc: 0.9870 - loss: 0.0388

 9964/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 418us/step - acc: 0.9870 - loss: 0.0388

10104/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 418us/step - acc: 0.9871 - loss: 0.0387

10241/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 417us/step - acc: 0.9871 - loss: 0.0386

10374/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 416us/step - acc: 0.9871 - loss: 0.0385

10508/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 416us/step - acc: 0.9871 - loss: 0.0385

10644/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 415us/step - acc: 0.9872 - loss: 0.0384

10778/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 415us/step - acc: 0.9872 - loss: 0.0383

10918/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 414us/step - acc: 0.9872 - loss: 0.0382

11051/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 414us/step - acc: 0.9872 - loss: 0.0382

11186/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 413us/step - acc: 0.9873 - loss: 0.0381

11321/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 413us/step - acc: 0.9873 - loss: 0.0381

11456/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 412us/step - acc: 0.9873 - loss: 0.0380

11595/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 412us/step - acc: 0.9873 - loss: 0.0379

11734/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 411us/step - acc: 0.9874 - loss: 0.0379

11871/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 410us/step - acc: 0.9874 - loss: 0.0378

12007/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 410us/step - acc: 0.9874 - loss: 0.0378

12137/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 410us/step - acc: 0.9874 - loss: 0.0377

12275/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 409us/step - acc: 0.9874 - loss: 0.0377

12415/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 409us/step - acc: 0.9874 - loss: 0.0376

12551/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 408us/step - acc: 0.9875 - loss: 0.0376

12685/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 408us/step - acc: 0.9875 - loss: 0.0375

12821/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 407us/step - acc: 0.9875 - loss: 0.0375

12957/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 407us/step - acc: 0.9875 - loss: 0.0374

13096/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 407us/step - acc: 0.9875 - loss: 0.0374

13236/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 406us/step - acc: 0.9875 - loss: 0.0374

13374/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 406us/step - acc: 0.9875 - loss: 0.0373

13498/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 406us/step - acc: 0.9875 - loss: 0.0373

13634/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 405us/step - acc: 0.9876 - loss: 0.0373

13772/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 405us/step - acc: 0.9876 - loss: 0.0372

13906/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 404us/step - acc: 0.9876 - loss: 0.0372

14044/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 404us/step - acc: 0.9876 - loss: 0.0371

14183/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 404us/step - acc: 0.9876 - loss: 0.0371

14322/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 403us/step - acc: 0.9876 - loss: 0.0371

14462/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 403us/step - acc: 0.9876 - loss: 0.0371

14600/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 402us/step - acc: 0.9876 - loss: 0.0370

14728/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 402us/step - acc: 0.9876 - loss: 0.0370

14865/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 402us/step - acc: 0.9876 - loss: 0.0370

15007/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 402us/step - acc: 0.9877 - loss: 0.0369

15131/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 402us/step - acc: 0.9877 - loss: 0.0369

15260/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 401us/step - acc: 0.9877 - loss: 0.0369

15390/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 401us/step - acc: 0.9877 - loss: 0.0368

15529/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 401us/step - acc: 0.9877 - loss: 0.0368

15654/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 401us/step - acc: 0.9877 - loss: 0.0368

15788/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 401us/step - acc: 0.9877 - loss: 0.0368

15928/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 400us/step - acc: 0.9877 - loss: 0.0367

16068/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 400us/step - acc: 0.9877 - loss: 0.0367

16205/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 400us/step - acc: 0.9877 - loss: 0.0367

16340/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 400us/step - acc: 0.9877 - loss: 0.0366

16476/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 399us/step - acc: 0.9878 - loss: 0.0366

16611/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 399us/step - acc: 0.9878 - loss: 0.0366

16749/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 399us/step - acc: 0.9878 - loss: 0.0366

16885/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 399us/step - acc: 0.9878 - loss: 0.0366

17021/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 398us/step - acc: 0.9878 - loss: 0.0365

17159/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 398us/step - acc: 0.9878 - loss: 0.0365

17296/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 398us/step - acc: 0.9878 - loss: 0.0365

17432/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 398us/step - acc: 0.9878 - loss: 0.0365

17569/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 397us/step - acc: 0.9878 - loss: 0.0365

17705/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 397us/step - acc: 0.9878 - loss: 0.0364

17842/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 397us/step - acc: 0.9878 - loss: 0.0364

17976/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 397us/step - acc: 0.9878 - loss: 0.0364

18111/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 397us/step - acc: 0.9878 - loss: 0.0364

18245/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 396us/step - acc: 0.9879 - loss: 0.0364

18380/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 396us/step - acc: 0.9879 - loss: 0.0363

18516/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 396us/step - acc: 0.9879 - loss: 0.0363

18653/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 396us/step - acc: 0.9879 - loss: 0.0363

18793/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 395us/step - acc: 0.9879 - loss: 0.0363

18929/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 395us/step - acc: 0.9879 - loss: 0.0363

19068/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 395us/step - acc: 0.9879 - loss: 0.0363

19204/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 395us/step - acc: 0.9879 - loss: 0.0363

19341/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 395us/step - acc: 0.9879 - loss: 0.0362

19477/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 394us/step - acc: 0.9879 - loss: 0.0362

19614/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 394us/step - acc: 0.9879 - loss: 0.0362

19751/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 394us/step - acc: 0.9879 - loss: 0.0362

19890/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 394us/step - acc: 0.9879 - loss: 0.0362

20023/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 394us/step - acc: 0.9879 - loss: 0.0362

20162/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 394us/step - acc: 0.9879 - loss: 0.0362

20299/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 393us/step - acc: 0.9880 - loss: 0.0361

20435/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 393us/step - acc: 0.9880 - loss: 0.0361

20571/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 393us/step - acc: 0.9880 - loss: 0.0361

20709/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 393us/step - acc: 0.9880 - loss: 0.0361

20842/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 393us/step - acc: 0.9880 - loss: 0.0361

20979/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 393us/step - acc: 0.9880 - loss: 0.0361

21116/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 392us/step - acc: 0.9880 - loss: 0.0361

21255/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 392us/step - acc: 0.9880 - loss: 0.0360

21393/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 392us/step - acc: 0.9880 - loss: 0.0360

21521/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 392us/step - acc: 0.9880 - loss: 0.0360

21654/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 392us/step - acc: 0.9880 - loss: 0.0360

21780/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 392us/step - acc: 0.9880 - loss: 0.0360

21914/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 392us/step - acc: 0.9880 - loss: 0.0360

22046/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 392us/step - acc: 0.9880 - loss: 0.0360

22179/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 392us/step - acc: 0.9880 - loss: 0.0360

22314/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 392us/step - acc: 0.9880 - loss: 0.0360

22453/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 391us/step - acc: 0.9880 - loss: 0.0360

22588/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 391us/step - acc: 0.9880 - loss: 0.0360

22726/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 391us/step - acc: 0.9880 - loss: 0.0360

22863/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 391us/step - acc: 0.9880 - loss: 0.0360

22999/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 391us/step - acc: 0.9880 - loss: 0.0360

23136/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 391us/step - acc: 0.9880 - loss: 0.0360

23275/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 390us/step - acc: 0.9880 - loss: 0.0360

23412/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 390us/step - acc: 0.9880 - loss: 0.0360

23544/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 390us/step - acc: 0.9880 - loss: 0.0360

23679/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 390us/step - acc: 0.9880 - loss: 0.0360

23817/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 390us/step - acc: 0.9880 - loss: 0.0360

23951/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 390us/step - acc: 0.9880 - loss: 0.0360

24089/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 390us/step - acc: 0.9880 - loss: 0.0360

24226/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 390us/step - acc: 0.9880 - loss: 0.0360

24364/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 389us/step - acc: 0.9880 - loss: 0.0360

24502/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 389us/step - acc: 0.9880 - loss: 0.0360

24639/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 389us/step - acc: 0.9880 - loss: 0.0360

24776/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 389us/step - acc: 0.9880 - loss: 0.0360

24909/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 389us/step - acc: 0.9880 - loss: 0.0360

25044/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 389us/step - acc: 0.9880 - loss: 0.0360

25178/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 389us/step - acc: 0.9880 - loss: 0.0360

25315/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 389us/step - acc: 0.9880 - loss: 0.0360

25453/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 389us/step - acc: 0.9880 - loss: 0.0360

25581/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 389us/step - acc: 0.9880 - loss: 0.0360

25717/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 388us/step - acc: 0.9880 - loss: 0.0360

25853/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 388us/step - acc: 0.9881 - loss: 0.0360

25991/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 388us/step - acc: 0.9881 - loss: 0.0360

26129/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 388us/step - acc: 0.9881 - loss: 0.0360

26263/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 388us/step - acc: 0.9881 - loss: 0.0360

26401/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 388us/step - acc: 0.9881 - loss: 0.0360

26537/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 388us/step - acc: 0.9881 - loss: 0.0360

26674/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 388us/step - acc: 0.9881 - loss: 0.0360

26813/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 388us/step - acc: 0.9881 - loss: 0.0360

26951/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 387us/step - acc: 0.9881 - loss: 0.0360

27089/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 387us/step - acc: 0.9880 - loss: 0.0360

27228/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 387us/step - acc: 0.9880 - loss: 0.0360

27365/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 387us/step - acc: 0.9880 - loss: 0.0360

27504/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 387us/step - acc: 0.9880 - loss: 0.0360

27644/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 387us/step - acc: 0.9880 - loss: 0.0360

27781/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 387us/step - acc: 0.9880 - loss: 0.0360

27918/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 387us/step - acc: 0.9880 - loss: 0.0360

28056/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 386us/step - acc: 0.9880 - loss: 0.0360

28194/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 386us/step - acc: 0.9880 - loss: 0.0361

28333/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 386us/step - acc: 0.9880 - loss: 0.0361

28468/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 386us/step - acc: 0.9880 - loss: 0.0361

28604/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 386us/step - acc: 0.9880 - loss: 0.0361

28743/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 386us/step - acc: 0.9880 - loss: 0.0361

28882/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 386us/step - acc: 0.9880 - loss: 0.0361

29017/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 386us/step - acc: 0.9880 - loss: 0.0361

29153/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 386us/step - acc: 0.9880 - loss: 0.0361

29293/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 386us/step - acc: 0.9880 - loss: 0.0361

29431/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 385us/step - acc: 0.9880 - loss: 0.0361

29567/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 385us/step - acc: 0.9880 - loss: 0.0361

29705/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 385us/step - acc: 0.9880 - loss: 0.0361

29843/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 385us/step - acc: 0.9880 - loss: 0.0361

29979/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 385us/step - acc: 0.9880 - loss: 0.0362

30115/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 385us/step - acc: 0.9880 - loss: 0.0362

30253/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 385us/step - acc: 0.9880 - loss: 0.0362

30386/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 385us/step - acc: 0.9880 - loss: 0.0362

30526/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 385us/step - acc: 0.9880 - loss: 0.0362

30662/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 385us/step - acc: 0.9880 - loss: 0.0362

30800/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 385us/step - acc: 0.9880 - loss: 0.0362

30937/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 385us/step - acc: 0.9880 - loss: 0.0362

31073/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 384us/step - acc: 0.9880 - loss: 0.0362

31210/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 384us/step - acc: 0.9880 - loss: 0.0362

31349/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 384us/step - acc: 0.9880 - loss: 0.0362

31488/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 384us/step - acc: 0.9880 - loss: 0.0363

31625/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 384us/step - acc: 0.9880 - loss: 0.0363

31760/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 384us/step - acc: 0.9880 - loss: 0.0363

31899/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 384us/step - acc: 0.9880 - loss: 0.0363

32041/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 384us/step - acc: 0.9880 - loss: 0.0363

32178/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 384us/step - acc: 0.9880 - loss: 0.0363

32313/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 384us/step - acc: 0.9879 - loss: 0.0363

32446/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 384us/step - acc: 0.9879 - loss: 0.0363

32584/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 384us/step - acc: 0.9879 - loss: 0.0363

32720/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 384us/step - acc: 0.9879 - loss: 0.0363

32855/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 383us/step - acc: 0.9879 - loss: 0.0363

32987/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 383us/step - acc: 0.9879 - loss: 0.0364

33121/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 383us/step - acc: 0.9879 - loss: 0.0364

33260/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 383us/step - acc: 0.9879 - loss: 0.0364

33397/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 383us/step - acc: 0.9879 - loss: 0.0364

33536/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 383us/step - acc: 0.9879 - loss: 0.0364

33674/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 383us/step - acc: 0.9879 - loss: 0.0364

33809/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 383us/step - acc: 0.9879 - loss: 0.0364

33949/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 383us/step - acc: 0.9879 - loss: 0.0364 

34088/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 383us/step - acc: 0.9879 - loss: 0.0364

34227/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 383us/step - acc: 0.9879 - loss: 0.0364

34362/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 383us/step - acc: 0.9879 - loss: 0.0365

34498/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 383us/step - acc: 0.9879 - loss: 0.0365

34633/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 383us/step - acc: 0.9879 - loss: 0.0365

34771/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 383us/step - acc: 0.9879 - loss: 0.0365

34910/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 382us/step - acc: 0.9879 - loss: 0.0365

35050/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 382us/step - acc: 0.9879 - loss: 0.0365

35175/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 382us/step - acc: 0.9879 - loss: 0.0365

35314/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 382us/step - acc: 0.9879 - loss: 0.0365

35453/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 382us/step - acc: 0.9879 - loss: 0.0365

35590/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 382us/step - acc: 0.9879 - loss: 0.0365

35728/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 382us/step - acc: 0.9879 - loss: 0.0366

35861/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 382us/step - acc: 0.9879 - loss: 0.0366

35996/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 382us/step - acc: 0.9879 - loss: 0.0366

36132/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 382us/step - acc: 0.9879 - loss: 0.0366

36268/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 382us/step - acc: 0.9879 - loss: 0.0366

36409/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 382us/step - acc: 0.9879 - loss: 0.0366

36547/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 382us/step - acc: 0.9878 - loss: 0.0366

36686/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 382us/step - acc: 0.9878 - loss: 0.0366

36824/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 382us/step - acc: 0.9878 - loss: 0.0366

36959/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 382us/step - acc: 0.9878 - loss: 0.0366

37097/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 382us/step - acc: 0.9878 - loss: 0.0366

37236/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 382us/step - acc: 0.9878 - loss: 0.0367

37370/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 381us/step - acc: 0.9878 - loss: 0.0367

37506/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 381us/step - acc: 0.9878 - loss: 0.0367

37638/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 381us/step - acc: 0.9878 - loss: 0.0367

37778/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 381us/step - acc: 0.9878 - loss: 0.0367

37915/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 381us/step - acc: 0.9878 - loss: 0.0367

38051/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 381us/step - acc: 0.9878 - loss: 0.0367

38183/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 381us/step - acc: 0.9878 - loss: 0.0367

38321/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 381us/step - acc: 0.9878 - loss: 0.0367

38460/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 381us/step - acc: 0.9878 - loss: 0.0367

38595/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 381us/step - acc: 0.9878 - loss: 0.0367

38733/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 381us/step - acc: 0.9878 - loss: 0.0367

38867/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 381us/step - acc: 0.9878 - loss: 0.0367

39005/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 381us/step - acc: 0.9878 - loss: 0.0368

39141/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 381us/step - acc: 0.9878 - loss: 0.0368

39280/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 381us/step - acc: 0.9878 - loss: 0.0368

39416/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 381us/step - acc: 0.9878 - loss: 0.0368

39552/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 381us/step - acc: 0.9878 - loss: 0.0368

39691/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 381us/step - acc: 0.9878 - loss: 0.0368

39828/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 381us/step - acc: 0.9878 - loss: 0.0368

39962/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 381us/step - acc: 0.9878 - loss: 0.0368

40099/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 381us/step - acc: 0.9878 - loss: 0.0368

40235/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 381us/step - acc: 0.9878 - loss: 0.0368

40371/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 380us/step - acc: 0.9878 - loss: 0.0368

40509/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 380us/step - acc: 0.9878 - loss: 0.0368

40646/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 380us/step - acc: 0.9878 - loss: 0.0368

40770/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 380us/step - acc: 0.9878 - loss: 0.0368

40909/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 380us/step - acc: 0.9878 - loss: 0.0369

41046/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 380us/step - acc: 0.9878 - loss: 0.0369

41183/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 380us/step - acc: 0.9878 - loss: 0.0369

41321/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 380us/step - acc: 0.9878 - loss: 0.0369

41459/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 380us/step - acc: 0.9878 - loss: 0.0369

41596/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 380us/step - acc: 0.9877 - loss: 0.0369

41733/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 380us/step - acc: 0.9877 - loss: 0.0369

41870/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 380us/step - acc: 0.9877 - loss: 0.0369

41913/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 381us/step - acc: 0.9877 - loss: 0.0369

42010/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 381us/step - acc: 0.9877 - loss: 0.0369

42131/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 381us/step - acc: 0.9877 - loss: 0.0369

42249/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 381us/step - acc: 0.9877 - loss: 0.0369

42366/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 382us/step - acc: 0.9877 - loss: 0.0369

42475/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 382us/step - acc: 0.9877 - loss: 0.0369

42589/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 382us/step - acc: 0.9877 - loss: 0.0369

42699/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 382us/step - acc: 0.9877 - loss: 0.0369

42815/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 382us/step - acc: 0.9877 - loss: 0.0369

42922/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 382us/step - acc: 0.9877 - loss: 0.0369

43040/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 383us/step - acc: 0.9877 - loss: 0.0369

43151/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 383us/step - acc: 0.9877 - loss: 0.0369

43268/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 383us/step - acc: 0.9877 - loss: 0.0369

43390/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 383us/step - acc: 0.9877 - loss: 0.0370

43525/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 383us/step - acc: 0.9877 - loss: 0.0370

43653/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 383us/step - acc: 0.9877 - loss: 0.0370

43791/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 383us/step - acc: 0.9877 - loss: 0.0370

43928/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 383us/step - acc: 0.9877 - loss: 0.0370

44056/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 383us/step - acc: 0.9877 - loss: 0.0370

44199/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 383us/step - acc: 0.9877 - loss: 0.0370

44333/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 383us/step - acc: 0.9877 - loss: 0.0370

44469/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 383us/step - acc: 0.9877 - loss: 0.0370

44608/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 383us/step - acc: 0.9877 - loss: 0.0370

44745/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 383us/step - acc: 0.9877 - loss: 0.0370

44883/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 383us/step - acc: 0.9877 - loss: 0.0370

45008/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 383us/step - acc: 0.9877 - loss: 0.0370

45141/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 383us/step - acc: 0.9877 - loss: 0.0370

45277/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 383us/step - acc: 0.9877 - loss: 0.0370

45414/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 382us/step - acc: 0.9877 - loss: 0.0370

45552/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 382us/step - acc: 0.9877 - loss: 0.0370

45687/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 382us/step - acc: 0.9877 - loss: 0.0370

45730/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 383us/step - acc: 0.9877 - loss: 0.0371

45865/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 383us/step - acc: 0.9877 - loss: 0.0371

46000/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 383us/step - acc: 0.9877 - loss: 0.0371

46130/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 383us/step - acc: 0.9877 - loss: 0.0371

46256/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 383us/step - acc: 0.9877 - loss: 0.0371

46389/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 383us/step - acc: 0.9877 - loss: 0.0371

46526/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 383us/step - acc: 0.9877 - loss: 0.0371

46656/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 383us/step - acc: 0.9877 - loss: 0.0371

46789/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 383us/step - acc: 0.9877 - loss: 0.0371

46924/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 383us/step - acc: 0.9877 - loss: 0.0371

47060/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9877 - loss: 0.0371

47197/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9877 - loss: 0.0371

47331/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9877 - loss: 0.0371

47464/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9877 - loss: 0.0371

47603/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9877 - loss: 0.0371

47739/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9877 - loss: 0.0371

47879/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9877 - loss: 0.0371

48010/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9877 - loss: 0.0371

48141/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9877 - loss: 0.0371

48278/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9877 - loss: 0.0371

48413/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9877 - loss: 0.0371

48550/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9877 - loss: 0.0371

48685/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9876 - loss: 0.0371

48823/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 383us/step - acc: 0.9876 - loss: 0.0371

48960/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 382us/step - acc: 0.9876 - loss: 0.0372

49098/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 382us/step - acc: 0.9876 - loss: 0.0372

49234/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 382us/step - acc: 0.9876 - loss: 0.0372

49370/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 382us/step - acc: 0.9876 - loss: 0.0372

49507/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 382us/step - acc: 0.9876 - loss: 0.0372

49632/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9876 - loss: 0.0372

49767/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9876 - loss: 0.0372

49898/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9876 - loss: 0.0372

50032/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9876 - loss: 0.0372

50167/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9876 - loss: 0.0372

50303/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9876 - loss: 0.0372

50439/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9876 - loss: 0.0372

50576/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9876 - loss: 0.0372

50713/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9876 - loss: 0.0372

50852/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9876 - loss: 0.0372

50988/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9876 - loss: 0.0372

51126/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9876 - loss: 0.0372

51250/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9876 - loss: 0.0372

51376/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9876 - loss: 0.0372

51505/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9876 - loss: 0.0372

51638/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9876 - loss: 0.0372

51772/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9876 - loss: 0.0372

51899/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9876 - loss: 0.0372

52033/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9876 - loss: 0.0372

52168/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0372

52290/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0372

52426/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0372

52561/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0373

52696/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0373

52829/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0373

52965/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0373

53094/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0373

53229/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0373

53367/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0373

53504/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0373

53641/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0373

53780/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0373

53917/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0373

54054/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0373

54186/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0373

54315/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0373

54451/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0373

54587/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0373

54723/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 382us/step - acc: 0.9876 - loss: 0.0373

54859/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 382us/step - acc: 0.9876 - loss: 0.0373

54994/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 382us/step - acc: 0.9876 - loss: 0.0373

55132/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 381us/step - acc: 0.9876 - loss: 0.0373

55267/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 381us/step - acc: 0.9876 - loss: 0.0374

55404/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 381us/step - acc: 0.9876 - loss: 0.0374

55539/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 381us/step - acc: 0.9876 - loss: 0.0374

55676/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 381us/step - acc: 0.9876 - loss: 0.0374

55814/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 381us/step - acc: 0.9876 - loss: 0.0374

55951/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 381us/step - acc: 0.9876 - loss: 0.0374

56089/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 381us/step - acc: 0.9876 - loss: 0.0374

56229/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 381us/step - acc: 0.9876 - loss: 0.0374

56368/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 381us/step - acc: 0.9876 - loss: 0.0374

56506/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 381us/step - acc: 0.9876 - loss: 0.0374

56642/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 381us/step - acc: 0.9876 - loss: 0.0374

56781/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 381us/step - acc: 0.9876 - loss: 0.0374

56918/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 381us/step - acc: 0.9875 - loss: 0.0374

57054/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 381us/step - acc: 0.9875 - loss: 0.0374

57191/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 381us/step - acc: 0.9875 - loss: 0.0374

57329/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 381us/step - acc: 0.9875 - loss: 0.0374

57465/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9875 - loss: 0.0374

57601/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9875 - loss: 0.0374

57732/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9875 - loss: 0.0374

57864/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9875 - loss: 0.0374

58002/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9875 - loss: 0.0374

58141/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9875 - loss: 0.0374

58274/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9875 - loss: 0.0374

58411/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9875 - loss: 0.0375

58550/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9875 - loss: 0.0375

58689/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9875 - loss: 0.0375

58829/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9875 - loss: 0.0375

58967/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 381us/step - acc: 0.9875 - loss: 0.0375

59106/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 380us/step - acc: 0.9875 - loss: 0.0375

59243/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 380us/step - acc: 0.9875 - loss: 0.0375

59379/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 380us/step - acc: 0.9875 - loss: 0.0375

59510/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 380us/step - acc: 0.9875 - loss: 0.0375

59636/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 380us/step - acc: 0.9875 - loss: 0.0375

59773/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 380us/step - acc: 0.9875 - loss: 0.0375

59899/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 380us/step - acc: 0.9875 - loss: 0.0375

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 441us/step - acc: 0.9875 - loss: 0.0375 - val_acc: 0.9699 - val_loss: 0.1140

Epoch 13/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 19:07 19ms/step - acc: 1.0000 - loss: 5.9605e-07

  117/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 433us/step - acc: 1.0000 - loss: 0.0159     

  226/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 446us/step - acc: 0.9975 - loss: 0.0195

  345/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 438us/step - acc: 0.9971 - loss: 0.0188

  469/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 429us/step - acc: 0.9966 - loss: 0.0196

  599/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 420us/step - acc: 0.9965 - loss: 0.0191

  723/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 417us/step - acc: 0.9966 - loss: 0.0186

  849/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 414us/step - acc: 0.9966 - loss: 0.0182

  970/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 414us/step - acc: 0.9966 - loss: 0.0182

 1079/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 419us/step - acc: 0.9966 - loss: 0.0185

 1200/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 419us/step - acc: 0.9964 - loss: 0.0191

 1322/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 418us/step - acc: 0.9963 - loss: 0.0195

 1445/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 417us/step - acc: 0.9961 - loss: 0.0198

 1577/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 414us/step - acc: 0.9960 - loss: 0.0201

 1695/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 415us/step - acc: 0.9958 - loss: 0.0206

 1817/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 415us/step - acc: 0.9956 - loss: 0.0210

 1933/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 416us/step - acc: 0.9954 - loss: 0.0214

 2063/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 414us/step - acc: 0.9952 - loss: 0.0218

 2178/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 415us/step - acc: 0.9950 - loss: 0.0222

 2298/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 415us/step - acc: 0.9948 - loss: 0.0225

 2376/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 423us/step - acc: 0.9947 - loss: 0.0227

 2494/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 423us/step - acc: 0.9945 - loss: 0.0230

 2611/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 423us/step - acc: 0.9944 - loss: 0.0233

 2730/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 423us/step - acc: 0.9942 - loss: 0.0235

 2847/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 423us/step - acc: 0.9941 - loss: 0.0237

 2957/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 425us/step - acc: 0.9939 - loss: 0.0239

 3072/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 425us/step - acc: 0.9938 - loss: 0.0241

 3186/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 426us/step - acc: 0.9937 - loss: 0.0242

 3309/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 425us/step - acc: 0.9936 - loss: 0.0244

 3408/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 427us/step - acc: 0.9935 - loss: 0.0246

 3528/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 427us/step - acc: 0.9934 - loss: 0.0248

 3646/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 427us/step - acc: 0.9933 - loss: 0.0250

 3765/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 427us/step - acc: 0.9932 - loss: 0.0251

 3888/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 426us/step - acc: 0.9932 - loss: 0.0253

 4000/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 427us/step - acc: 0.9931 - loss: 0.0254

 4118/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 427us/step - acc: 0.9930 - loss: 0.0255

 4241/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 426us/step - acc: 0.9930 - loss: 0.0257

 4362/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 426us/step - acc: 0.9929 - loss: 0.0258

 4480/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 426us/step - acc: 0.9929 - loss: 0.0259

 4595/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 426us/step - acc: 0.9928 - loss: 0.0259

 4721/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 425us/step - acc: 0.9928 - loss: 0.0260

 4844/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 425us/step - acc: 0.9927 - loss: 0.0261

 4970/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 424us/step - acc: 0.9927 - loss: 0.0262

 5083/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 425us/step - acc: 0.9927 - loss: 0.0263

 5200/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 425us/step - acc: 0.9926 - loss: 0.0264

 5313/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 425us/step - acc: 0.9926 - loss: 0.0265

 5431/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 425us/step - acc: 0.9925 - loss: 0.0266

 5547/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 425us/step - acc: 0.9925 - loss: 0.0267

 5681/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 424us/step - acc: 0.9925 - loss: 0.0269

 5816/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 423us/step - acc: 0.9924 - loss: 0.0270

 5948/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 422us/step - acc: 0.9924 - loss: 0.0271

 6087/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 421us/step - acc: 0.9923 - loss: 0.0272

 6218/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 420us/step - acc: 0.9923 - loss: 0.0273

 6354/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 419us/step - acc: 0.9922 - loss: 0.0275

 6486/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 418us/step - acc: 0.9922 - loss: 0.0276

 6618/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 417us/step - acc: 0.9921 - loss: 0.0277

 6755/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 416us/step - acc: 0.9921 - loss: 0.0278

 6892/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 415us/step - acc: 0.9920 - loss: 0.0279

 7028/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 414us/step - acc: 0.9920 - loss: 0.0280

 7165/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 413us/step - acc: 0.9919 - loss: 0.0281

 7301/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 413us/step - acc: 0.9918 - loss: 0.0283

 7439/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 412us/step - acc: 0.9918 - loss: 0.0284

 7577/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 411us/step - acc: 0.9917 - loss: 0.0285

 7711/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 410us/step - acc: 0.9916 - loss: 0.0286

 7848/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 409us/step - acc: 0.9916 - loss: 0.0287

 7982/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 409us/step - acc: 0.9915 - loss: 0.0288

 8109/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 409us/step - acc: 0.9915 - loss: 0.0289

 8246/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 408us/step - acc: 0.9914 - loss: 0.0291

 8381/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 407us/step - acc: 0.9914 - loss: 0.0292

 8498/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 408us/step - acc: 0.9913 - loss: 0.0292

 8623/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 408us/step - acc: 0.9913 - loss: 0.0293

 8761/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 407us/step - acc: 0.9913 - loss: 0.0294

 8898/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 406us/step - acc: 0.9912 - loss: 0.0295

 9036/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 406us/step - acc: 0.9912 - loss: 0.0296

 9167/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 405us/step - acc: 0.9911 - loss: 0.0297

 9301/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 405us/step - acc: 0.9911 - loss: 0.0298

 9439/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 404us/step - acc: 0.9911 - loss: 0.0298

 9577/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 404us/step - acc: 0.9910 - loss: 0.0299

 9716/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 403us/step - acc: 0.9910 - loss: 0.0300

 9853/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 402us/step - acc: 0.9909 - loss: 0.0301

 9991/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 402us/step - acc: 0.9909 - loss: 0.0301

10128/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 401us/step - acc: 0.9909 - loss: 0.0302

10263/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 401us/step - acc: 0.9909 - loss: 0.0302

10400/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 401us/step - acc: 0.9908 - loss: 0.0303

10534/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 400us/step - acc: 0.9908 - loss: 0.0303

10673/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 400us/step - acc: 0.9908 - loss: 0.0304

10811/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 399us/step - acc: 0.9908 - loss: 0.0304

10947/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 399us/step - acc: 0.9908 - loss: 0.0304

11085/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 398us/step - acc: 0.9907 - loss: 0.0305

11213/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 398us/step - acc: 0.9907 - loss: 0.0305

11351/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 398us/step - acc: 0.9907 - loss: 0.0305

11488/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 398us/step - acc: 0.9907 - loss: 0.0306

11625/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 397us/step - acc: 0.9907 - loss: 0.0306

11761/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 397us/step - acc: 0.9907 - loss: 0.0306

11897/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 397us/step - acc: 0.9906 - loss: 0.0306

12035/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 396us/step - acc: 0.9906 - loss: 0.0307

12175/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 396us/step - acc: 0.9906 - loss: 0.0307

12312/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 395us/step - acc: 0.9906 - loss: 0.0307

12451/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 395us/step - acc: 0.9906 - loss: 0.0307

12589/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 395us/step - acc: 0.9906 - loss: 0.0308

12726/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 394us/step - acc: 0.9905 - loss: 0.0308

12863/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 394us/step - acc: 0.9905 - loss: 0.0308

12999/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 394us/step - acc: 0.9905 - loss: 0.0308

13138/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 393us/step - acc: 0.9905 - loss: 0.0308

13272/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 393us/step - acc: 0.9905 - loss: 0.0308

13408/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 393us/step - acc: 0.9905 - loss: 0.0309

13545/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 393us/step - acc: 0.9905 - loss: 0.0309

13683/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 392us/step - acc: 0.9905 - loss: 0.0309

13819/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 392us/step - acc: 0.9904 - loss: 0.0309

13957/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 392us/step - acc: 0.9904 - loss: 0.0309

14095/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 392us/step - acc: 0.9904 - loss: 0.0310

14233/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 391us/step - acc: 0.9904 - loss: 0.0310

14371/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 391us/step - acc: 0.9904 - loss: 0.0310

14510/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 391us/step - acc: 0.9904 - loss: 0.0310

14651/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 390us/step - acc: 0.9904 - loss: 0.0310

14792/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 390us/step - acc: 0.9903 - loss: 0.0311

14930/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 390us/step - acc: 0.9903 - loss: 0.0311

15068/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 390us/step - acc: 0.9903 - loss: 0.0311

15207/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 389us/step - acc: 0.9903 - loss: 0.0311

15347/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 389us/step - acc: 0.9903 - loss: 0.0311

15485/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 389us/step - acc: 0.9903 - loss: 0.0312

15623/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 389us/step - acc: 0.9903 - loss: 0.0312

15762/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 388us/step - acc: 0.9902 - loss: 0.0312

15897/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 388us/step - acc: 0.9902 - loss: 0.0312

16030/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 388us/step - acc: 0.9902 - loss: 0.0312

16160/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 388us/step - acc: 0.9902 - loss: 0.0313

16286/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 388us/step - acc: 0.9902 - loss: 0.0313

16412/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 388us/step - acc: 0.9902 - loss: 0.0313

16534/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 389us/step - acc: 0.9902 - loss: 0.0313

16657/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 389us/step - acc: 0.9902 - loss: 0.0313

16778/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 389us/step - acc: 0.9902 - loss: 0.0313

16899/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 389us/step - acc: 0.9902 - loss: 0.0314

17026/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 389us/step - acc: 0.9902 - loss: 0.0314

17149/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 389us/step - acc: 0.9902 - loss: 0.0314

17269/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 389us/step - acc: 0.9901 - loss: 0.0314

17388/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 390us/step - acc: 0.9901 - loss: 0.0314

17512/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 390us/step - acc: 0.9901 - loss: 0.0314

17636/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 390us/step - acc: 0.9901 - loss: 0.0314

17755/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 390us/step - acc: 0.9901 - loss: 0.0315

17878/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 390us/step - acc: 0.9901 - loss: 0.0315

17994/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 391us/step - acc: 0.9901 - loss: 0.0315

18113/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 391us/step - acc: 0.9901 - loss: 0.0315

18239/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 391us/step - acc: 0.9901 - loss: 0.0315

18362/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 391us/step - acc: 0.9901 - loss: 0.0315

18480/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 391us/step - acc: 0.9901 - loss: 0.0316

18607/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 391us/step - acc: 0.9901 - loss: 0.0316

18726/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 391us/step - acc: 0.9901 - loss: 0.0316

18851/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 391us/step - acc: 0.9900 - loss: 0.0316

18971/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 392us/step - acc: 0.9900 - loss: 0.0316

19092/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 392us/step - acc: 0.9900 - loss: 0.0317

19214/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 392us/step - acc: 0.9900 - loss: 0.0317

19328/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 392us/step - acc: 0.9900 - loss: 0.0317

19449/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 392us/step - acc: 0.9900 - loss: 0.0317

19568/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 392us/step - acc: 0.9900 - loss: 0.0317

19683/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 393us/step - acc: 0.9900 - loss: 0.0317

19808/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 393us/step - acc: 0.9900 - loss: 0.0317

19924/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 393us/step - acc: 0.9900 - loss: 0.0318

20041/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 393us/step - acc: 0.9900 - loss: 0.0318

20164/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 393us/step - acc: 0.9900 - loss: 0.0318

20271/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 394us/step - acc: 0.9900 - loss: 0.0318

20392/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 394us/step - acc: 0.9900 - loss: 0.0318

20512/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 394us/step - acc: 0.9900 - loss: 0.0318

20630/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 394us/step - acc: 0.9900 - loss: 0.0318

20748/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 394us/step - acc: 0.9900 - loss: 0.0318

20870/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 394us/step - acc: 0.9900 - loss: 0.0318

20981/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 395us/step - acc: 0.9900 - loss: 0.0318

21096/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 395us/step - acc: 0.9900 - loss: 0.0319

21219/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 395us/step - acc: 0.9899 - loss: 0.0319

21336/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 395us/step - acc: 0.9899 - loss: 0.0319

21458/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 395us/step - acc: 0.9899 - loss: 0.0319

21575/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 395us/step - acc: 0.9899 - loss: 0.0319

21684/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 396us/step - acc: 0.9899 - loss: 0.0319

21799/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 396us/step - acc: 0.9899 - loss: 0.0319

21908/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 396us/step - acc: 0.9899 - loss: 0.0319

22029/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 396us/step - acc: 0.9899 - loss: 0.0319

22138/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 397us/step - acc: 0.9899 - loss: 0.0320

22242/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 397us/step - acc: 0.9899 - loss: 0.0320

22327/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 398us/step - acc: 0.9899 - loss: 0.0320

22440/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 398us/step - acc: 0.9899 - loss: 0.0320

22562/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 398us/step - acc: 0.9899 - loss: 0.0320

22671/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 399us/step - acc: 0.9899 - loss: 0.0320

22790/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 399us/step - acc: 0.9899 - loss: 0.0320

22913/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 399us/step - acc: 0.9899 - loss: 0.0320

23030/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 399us/step - acc: 0.9899 - loss: 0.0320

23155/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 399us/step - acc: 0.9899 - loss: 0.0320

23275/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 399us/step - acc: 0.9899 - loss: 0.0321

23390/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 399us/step - acc: 0.9899 - loss: 0.0321

23510/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 399us/step - acc: 0.9899 - loss: 0.0321

23621/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 400us/step - acc: 0.9899 - loss: 0.0321

23680/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 401us/step - acc: 0.9898 - loss: 0.0321

23790/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 401us/step - acc: 0.9898 - loss: 0.0321

23904/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 401us/step - acc: 0.9898 - loss: 0.0321

24016/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 401us/step - acc: 0.9898 - loss: 0.0321

24126/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 402us/step - acc: 0.9898 - loss: 0.0321

24233/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 402us/step - acc: 0.9898 - loss: 0.0321

24355/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 402us/step - acc: 0.9898 - loss: 0.0321

24471/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 402us/step - acc: 0.9898 - loss: 0.0321

24589/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 402us/step - acc: 0.9898 - loss: 0.0321

24670/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 403us/step - acc: 0.9898 - loss: 0.0321

24778/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 403us/step - acc: 0.9898 - loss: 0.0321

24903/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 403us/step - acc: 0.9898 - loss: 0.0321

25031/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 403us/step - acc: 0.9898 - loss: 0.0322

25157/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 403us/step - acc: 0.9898 - loss: 0.0322

25280/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 403us/step - acc: 0.9898 - loss: 0.0322

25398/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 403us/step - acc: 0.9898 - loss: 0.0322

25521/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 403us/step - acc: 0.9898 - loss: 0.0322

25646/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 403us/step - acc: 0.9898 - loss: 0.0322

25770/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 403us/step - acc: 0.9898 - loss: 0.0322

25885/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 403us/step - acc: 0.9898 - loss: 0.0322

26003/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 403us/step - acc: 0.9898 - loss: 0.0322

26121/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 404us/step - acc: 0.9898 - loss: 0.0322

26245/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 404us/step - acc: 0.9898 - loss: 0.0323

26363/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 404us/step - acc: 0.9898 - loss: 0.0323

26492/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 404us/step - acc: 0.9898 - loss: 0.0323

26625/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 403us/step - acc: 0.9898 - loss: 0.0323

26763/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 403us/step - acc: 0.9898 - loss: 0.0323

26899/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 403us/step - acc: 0.9898 - loss: 0.0323

27038/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 403us/step - acc: 0.9898 - loss: 0.0323

27173/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 403us/step - acc: 0.9897 - loss: 0.0323

27310/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 403us/step - acc: 0.9897 - loss: 0.0323

27450/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 402us/step - acc: 0.9897 - loss: 0.0323

27589/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 402us/step - acc: 0.9897 - loss: 0.0323

27724/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 402us/step - acc: 0.9897 - loss: 0.0323

27861/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 402us/step - acc: 0.9897 - loss: 0.0324

27998/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 402us/step - acc: 0.9897 - loss: 0.0324

28132/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 401us/step - acc: 0.9897 - loss: 0.0324

28262/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 401us/step - acc: 0.9897 - loss: 0.0324

28401/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 401us/step - acc: 0.9897 - loss: 0.0324

28525/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 401us/step - acc: 0.9897 - loss: 0.0324

28655/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 401us/step - acc: 0.9897 - loss: 0.0324

28788/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 401us/step - acc: 0.9897 - loss: 0.0324

28926/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 401us/step - acc: 0.9897 - loss: 0.0324

29046/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 401us/step - acc: 0.9897 - loss: 0.0324

29166/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 401us/step - acc: 0.9897 - loss: 0.0324

29283/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 401us/step - acc: 0.9897 - loss: 0.0324

29394/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 401us/step - acc: 0.9897 - loss: 0.0324

29508/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 401us/step - acc: 0.9897 - loss: 0.0325

29643/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 401us/step - acc: 0.9897 - loss: 0.0325

29780/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 401us/step - acc: 0.9897 - loss: 0.0325

29918/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 401us/step - acc: 0.9897 - loss: 0.0325

30054/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 401us/step - acc: 0.9897 - loss: 0.0325

30189/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 401us/step - acc: 0.9897 - loss: 0.0325

30327/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 401us/step - acc: 0.9897 - loss: 0.0325

30463/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 400us/step - acc: 0.9897 - loss: 0.0325

30599/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 400us/step - acc: 0.9897 - loss: 0.0325

30738/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 400us/step - acc: 0.9897 - loss: 0.0325

30876/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 400us/step - acc: 0.9897 - loss: 0.0325

31016/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 400us/step - acc: 0.9897 - loss: 0.0326

31157/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 400us/step - acc: 0.9897 - loss: 0.0326

31296/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 399us/step - acc: 0.9897 - loss: 0.0326

31433/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 399us/step - acc: 0.9897 - loss: 0.0326

31560/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 399us/step - acc: 0.9897 - loss: 0.0326

31700/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 399us/step - acc: 0.9896 - loss: 0.0326

31834/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 399us/step - acc: 0.9896 - loss: 0.0326

31972/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 399us/step - acc: 0.9896 - loss: 0.0326

32110/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 399us/step - acc: 0.9896 - loss: 0.0326

32250/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 398us/step - acc: 0.9896 - loss: 0.0326

32389/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 398us/step - acc: 0.9896 - loss: 0.0326

32528/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 398us/step - acc: 0.9896 - loss: 0.0326

32667/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 398us/step - acc: 0.9896 - loss: 0.0326

32805/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 398us/step - acc: 0.9896 - loss: 0.0326

32944/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 398us/step - acc: 0.9896 - loss: 0.0327

33076/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 398us/step - acc: 0.9896 - loss: 0.0327

33211/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 398us/step - acc: 0.9896 - loss: 0.0327

33350/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 397us/step - acc: 0.9896 - loss: 0.0327

33489/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 397us/step - acc: 0.9896 - loss: 0.0327

33626/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 397us/step - acc: 0.9896 - loss: 0.0327

33763/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 397us/step - acc: 0.9896 - loss: 0.0327

33900/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 397us/step - acc: 0.9896 - loss: 0.0327

34036/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 397us/step - acc: 0.9896 - loss: 0.0327

34174/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 397us/step - acc: 0.9896 - loss: 0.0327

34311/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 396us/step - acc: 0.9896 - loss: 0.0327

34447/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 396us/step - acc: 0.9896 - loss: 0.0327

34585/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 396us/step - acc: 0.9896 - loss: 0.0327

34722/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 396us/step - acc: 0.9896 - loss: 0.0327

34860/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 396us/step - acc: 0.9896 - loss: 0.0327 

34999/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 396us/step - acc: 0.9896 - loss: 0.0327

35135/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 396us/step - acc: 0.9896 - loss: 0.0327

35271/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 396us/step - acc: 0.9896 - loss: 0.0327

35412/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 395us/step - acc: 0.9896 - loss: 0.0327

35549/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 395us/step - acc: 0.9896 - loss: 0.0327

35686/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 395us/step - acc: 0.9896 - loss: 0.0327

35824/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 395us/step - acc: 0.9896 - loss: 0.0328

35957/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 395us/step - acc: 0.9896 - loss: 0.0328

36095/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 395us/step - acc: 0.9896 - loss: 0.0328

36232/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 395us/step - acc: 0.9896 - loss: 0.0328

36370/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 395us/step - acc: 0.9896 - loss: 0.0328

36508/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 395us/step - acc: 0.9896 - loss: 0.0328

36641/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 395us/step - acc: 0.9896 - loss: 0.0328

36780/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 394us/step - acc: 0.9896 - loss: 0.0328

36917/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 394us/step - acc: 0.9896 - loss: 0.0328

37055/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 394us/step - acc: 0.9896 - loss: 0.0328

37190/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 394us/step - acc: 0.9896 - loss: 0.0328

37326/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 394us/step - acc: 0.9896 - loss: 0.0328

37464/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 394us/step - acc: 0.9896 - loss: 0.0328

37602/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 394us/step - acc: 0.9896 - loss: 0.0328

37739/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 394us/step - acc: 0.9896 - loss: 0.0328

37876/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 394us/step - acc: 0.9896 - loss: 0.0328

38012/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 394us/step - acc: 0.9896 - loss: 0.0328

38151/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 393us/step - acc: 0.9896 - loss: 0.0328

38286/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 393us/step - acc: 0.9896 - loss: 0.0328

38424/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 393us/step - acc: 0.9896 - loss: 0.0328

38560/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 393us/step - acc: 0.9896 - loss: 0.0328

38693/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 393us/step - acc: 0.9896 - loss: 0.0328

38831/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 393us/step - acc: 0.9896 - loss: 0.0328

38968/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 393us/step - acc: 0.9896 - loss: 0.0328

39103/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 393us/step - acc: 0.9896 - loss: 0.0328

39243/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 393us/step - acc: 0.9896 - loss: 0.0328

39381/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 393us/step - acc: 0.9896 - loss: 0.0328

39519/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 392us/step - acc: 0.9896 - loss: 0.0328

39656/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 392us/step - acc: 0.9896 - loss: 0.0328

39795/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 392us/step - acc: 0.9896 - loss: 0.0328

39932/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 392us/step - acc: 0.9896 - loss: 0.0328

40067/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 392us/step - acc: 0.9896 - loss: 0.0328

40206/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 392us/step - acc: 0.9896 - loss: 0.0328

40345/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 392us/step - acc: 0.9896 - loss: 0.0328

40481/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 392us/step - acc: 0.9896 - loss: 0.0328

40620/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 392us/step - acc: 0.9896 - loss: 0.0328

40758/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 392us/step - acc: 0.9896 - loss: 0.0328

40896/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 392us/step - acc: 0.9896 - loss: 0.0328

41032/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 391us/step - acc: 0.9896 - loss: 0.0328

41168/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 391us/step - acc: 0.9896 - loss: 0.0328

41306/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 391us/step - acc: 0.9896 - loss: 0.0328

41442/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 391us/step - acc: 0.9896 - loss: 0.0328

41581/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 391us/step - acc: 0.9895 - loss: 0.0328

41719/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 391us/step - acc: 0.9895 - loss: 0.0328

41856/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 391us/step - acc: 0.9895 - loss: 0.0328

41994/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 391us/step - acc: 0.9895 - loss: 0.0328

42130/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 391us/step - acc: 0.9895 - loss: 0.0328

42264/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 391us/step - acc: 0.9895 - loss: 0.0328

42401/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 391us/step - acc: 0.9895 - loss: 0.0328

42540/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 391us/step - acc: 0.9895 - loss: 0.0328

42676/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 390us/step - acc: 0.9895 - loss: 0.0328

42813/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 390us/step - acc: 0.9895 - loss: 0.0328

42951/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 390us/step - acc: 0.9895 - loss: 0.0328

43084/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 390us/step - acc: 0.9895 - loss: 0.0328

43219/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 390us/step - acc: 0.9895 - loss: 0.0328

43355/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 390us/step - acc: 0.9895 - loss: 0.0328

43493/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 390us/step - acc: 0.9895 - loss: 0.0328

43631/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 390us/step - acc: 0.9895 - loss: 0.0328

43759/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 390us/step - acc: 0.9895 - loss: 0.0328

43884/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 390us/step - acc: 0.9895 - loss: 0.0328

44022/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 390us/step - acc: 0.9895 - loss: 0.0328

44154/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 390us/step - acc: 0.9895 - loss: 0.0328

44291/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 390us/step - acc: 0.9895 - loss: 0.0328

44427/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 390us/step - acc: 0.9895 - loss: 0.0328

44563/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 390us/step - acc: 0.9895 - loss: 0.0328

44701/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 390us/step - acc: 0.9895 - loss: 0.0328

44834/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 390us/step - acc: 0.9895 - loss: 0.0328

44971/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 390us/step - acc: 0.9895 - loss: 0.0328

45106/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 389us/step - acc: 0.9895 - loss: 0.0328

45244/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 389us/step - acc: 0.9895 - loss: 0.0328

45382/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 389us/step - acc: 0.9895 - loss: 0.0328

45518/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 389us/step - acc: 0.9895 - loss: 0.0328

45657/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 389us/step - acc: 0.9895 - loss: 0.0328

45795/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 389us/step - acc: 0.9895 - loss: 0.0328

45933/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 389us/step - acc: 0.9895 - loss: 0.0328

46070/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 389us/step - acc: 0.9895 - loss: 0.0328

46208/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 389us/step - acc: 0.9895 - loss: 0.0328

46346/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 389us/step - acc: 0.9895 - loss: 0.0328

46485/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 389us/step - acc: 0.9895 - loss: 0.0328

46622/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 389us/step - acc: 0.9895 - loss: 0.0328

46760/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 389us/step - acc: 0.9895 - loss: 0.0328

46892/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 389us/step - acc: 0.9895 - loss: 0.0328

47026/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 389us/step - acc: 0.9895 - loss: 0.0328

47162/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 388us/step - acc: 0.9895 - loss: 0.0328

47302/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 388us/step - acc: 0.9895 - loss: 0.0328

47440/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 388us/step - acc: 0.9895 - loss: 0.0328

47579/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 388us/step - acc: 0.9895 - loss: 0.0328

47718/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 388us/step - acc: 0.9895 - loss: 0.0328

47855/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 388us/step - acc: 0.9895 - loss: 0.0328

47992/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 388us/step - acc: 0.9895 - loss: 0.0328

48129/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 388us/step - acc: 0.9895 - loss: 0.0328

48263/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 388us/step - acc: 0.9895 - loss: 0.0328

48401/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 388us/step - acc: 0.9895 - loss: 0.0328

48543/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 388us/step - acc: 0.9895 - loss: 0.0328

48682/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 388us/step - acc: 0.9895 - loss: 0.0328

48826/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 388us/step - acc: 0.9895 - loss: 0.0328

48971/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 387us/step - acc: 0.9895 - loss: 0.0328

49112/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 387us/step - acc: 0.9895 - loss: 0.0328

49250/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 387us/step - acc: 0.9895 - loss: 0.0328

49381/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 387us/step - acc: 0.9895 - loss: 0.0328

49517/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 387us/step - acc: 0.9895 - loss: 0.0328

49653/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 387us/step - acc: 0.9895 - loss: 0.0328

49792/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 387us/step - acc: 0.9895 - loss: 0.0328

49930/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 387us/step - acc: 0.9895 - loss: 0.0328

50065/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 387us/step - acc: 0.9895 - loss: 0.0328

50204/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 387us/step - acc: 0.9895 - loss: 0.0328

50331/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 387us/step - acc: 0.9895 - loss: 0.0328

50469/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 387us/step - acc: 0.9895 - loss: 0.0328

50607/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 387us/step - acc: 0.9895 - loss: 0.0328

50745/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 387us/step - acc: 0.9895 - loss: 0.0328

50881/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 387us/step - acc: 0.9895 - loss: 0.0328

51014/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 387us/step - acc: 0.9895 - loss: 0.0328

51152/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 387us/step - acc: 0.9895 - loss: 0.0328

51289/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 387us/step - acc: 0.9895 - loss: 0.0329

51421/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 387us/step - acc: 0.9895 - loss: 0.0329

51560/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 386us/step - acc: 0.9895 - loss: 0.0329

51700/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 386us/step - acc: 0.9895 - loss: 0.0329

51840/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 386us/step - acc: 0.9895 - loss: 0.0329

51976/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 386us/step - acc: 0.9895 - loss: 0.0329

52112/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 386us/step - acc: 0.9894 - loss: 0.0329

52251/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9894 - loss: 0.0329

52387/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9894 - loss: 0.0329

52526/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9894 - loss: 0.0329

52661/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9894 - loss: 0.0329

52798/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9894 - loss: 0.0329

52935/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9894 - loss: 0.0329

53071/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9894 - loss: 0.0329

53210/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9894 - loss: 0.0329

53347/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9894 - loss: 0.0329

53482/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9894 - loss: 0.0329

53624/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9894 - loss: 0.0329

53764/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9894 - loss: 0.0329

53902/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9894 - loss: 0.0329

54041/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 385us/step - acc: 0.9894 - loss: 0.0329

54181/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 385us/step - acc: 0.9894 - loss: 0.0329

54320/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 385us/step - acc: 0.9894 - loss: 0.0329

54463/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 385us/step - acc: 0.9894 - loss: 0.0329

54606/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 385us/step - acc: 0.9894 - loss: 0.0330

54750/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 385us/step - acc: 0.9894 - loss: 0.0330

54891/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 385us/step - acc: 0.9894 - loss: 0.0330

55018/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 385us/step - acc: 0.9894 - loss: 0.0330

55153/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 385us/step - acc: 0.9894 - loss: 0.0330

55292/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 385us/step - acc: 0.9894 - loss: 0.0330

55431/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 385us/step - acc: 0.9894 - loss: 0.0330

55573/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 385us/step - acc: 0.9894 - loss: 0.0330

55714/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 385us/step - acc: 0.9894 - loss: 0.0330

55853/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 385us/step - acc: 0.9894 - loss: 0.0330

55991/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 385us/step - acc: 0.9894 - loss: 0.0330

56129/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 385us/step - acc: 0.9894 - loss: 0.0330

56266/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9894 - loss: 0.0330

56404/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9894 - loss: 0.0330

56541/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9894 - loss: 0.0330

56680/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9894 - loss: 0.0330

56820/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9894 - loss: 0.0330

56964/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9894 - loss: 0.0330

57103/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9894 - loss: 0.0330

57242/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9894 - loss: 0.0330

57381/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 384us/step - acc: 0.9894 - loss: 0.0330

57521/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 384us/step - acc: 0.9894 - loss: 0.0330

57660/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 384us/step - acc: 0.9894 - loss: 0.0331

57795/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 384us/step - acc: 0.9894 - loss: 0.0331

57934/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 384us/step - acc: 0.9894 - loss: 0.0331

58070/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 384us/step - acc: 0.9894 - loss: 0.0331

58207/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 384us/step - acc: 0.9893 - loss: 0.0331

58347/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 384us/step - acc: 0.9893 - loss: 0.0331

58486/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 384us/step - acc: 0.9893 - loss: 0.0331

58626/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 384us/step - acc: 0.9893 - loss: 0.0331

58769/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 383us/step - acc: 0.9893 - loss: 0.0331

58912/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 383us/step - acc: 0.9893 - loss: 0.0331

59054/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 383us/step - acc: 0.9893 - loss: 0.0331

59197/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 383us/step - acc: 0.9893 - loss: 0.0331

59340/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 383us/step - acc: 0.9893 - loss: 0.0331

59483/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 383us/step - acc: 0.9893 - loss: 0.0331

59628/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 383us/step - acc: 0.9893 - loss: 0.0331

59770/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 383us/step - acc: 0.9893 - loss: 0.0331

59912/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 383us/step - acc: 0.9893 - loss: 0.0331

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 442us/step - acc: 0.9893 - loss: 0.0331 - val_acc: 0.9720 - val_loss: 0.1097

Epoch 14/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 10:18 10ms/step - acc: 1.0000 - loss: 1.1325e-05

  127/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 399us/step - acc: 0.9999 - loss: 0.0024     

  260/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 387us/step - acc: 0.9945 - loss: 0.0169

  393/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 384us/step - acc: 0.9932 - loss: 0.0192

  529/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 380us/step - acc: 0.9925 - loss: 0.0205

  669/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 376us/step - acc: 0.9921 - loss: 0.0210

  804/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 375us/step - acc: 0.9920 - loss: 0.0209

  940/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 374us/step - acc: 0.9920 - loss: 0.0210

 1077/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 373us/step - acc: 0.9919 - loss: 0.0212

 1216/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 372us/step - acc: 0.9919 - loss: 0.0212

 1357/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 370us/step - acc: 0.9918 - loss: 0.0215

 1491/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 370us/step - acc: 0.9918 - loss: 0.0218

 1609/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 374us/step - acc: 0.9917 - loss: 0.0220

 1739/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 375us/step - acc: 0.9918 - loss: 0.0221

 1865/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 377us/step - acc: 0.9918 - loss: 0.0223

 1989/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 379us/step - acc: 0.9918 - loss: 0.0226

 2116/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 379us/step - acc: 0.9917 - loss: 0.0229

 2240/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 381us/step - acc: 0.9917 - loss: 0.0231

 2374/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 381us/step - acc: 0.9916 - loss: 0.0232

 2508/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 380us/step - acc: 0.9916 - loss: 0.0234

 2643/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 380us/step - acc: 0.9916 - loss: 0.0236

 2783/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 379us/step - acc: 0.9916 - loss: 0.0237

 2922/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 378us/step - acc: 0.9916 - loss: 0.0237

 3057/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 378us/step - acc: 0.9916 - loss: 0.0238

 3197/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 377us/step - acc: 0.9916 - loss: 0.0238

 3335/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 376us/step - acc: 0.9916 - loss: 0.0238

 3476/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 375us/step - acc: 0.9916 - loss: 0.0239

 3617/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 375us/step - acc: 0.9916 - loss: 0.0240

 3757/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 374us/step - acc: 0.9916 - loss: 0.0240

 3886/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 374us/step - acc: 0.9916 - loss: 0.0241

 4015/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9916 - loss: 0.0242

 4144/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9916 - loss: 0.0244

 4273/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 376us/step - acc: 0.9916 - loss: 0.0245

 4401/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 376us/step - acc: 0.9916 - loss: 0.0246

 4536/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 376us/step - acc: 0.9916 - loss: 0.0246

 4668/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 376us/step - acc: 0.9915 - loss: 0.0247

 4805/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 376us/step - acc: 0.9915 - loss: 0.0248

 4948/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9915 - loss: 0.0249

 5090/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9915 - loss: 0.0249

 5219/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9915 - loss: 0.0250

 5352/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9915 - loss: 0.0251

 5485/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9915 - loss: 0.0251

 5615/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 375us/step - acc: 0.9915 - loss: 0.0252

 5743/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 376us/step - acc: 0.9915 - loss: 0.0252

 5873/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 376us/step - acc: 0.9915 - loss: 0.0253

 6005/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 376us/step - acc: 0.9915 - loss: 0.0253

 6132/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 377us/step - acc: 0.9915 - loss: 0.0253

 6264/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 377us/step - acc: 0.9915 - loss: 0.0254

 6395/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 377us/step - acc: 0.9915 - loss: 0.0255

 6530/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 377us/step - acc: 0.9915 - loss: 0.0256

 6666/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 377us/step - acc: 0.9914 - loss: 0.0256

 6807/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 376us/step - acc: 0.9914 - loss: 0.0257

 6933/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 377us/step - acc: 0.9914 - loss: 0.0258

 7049/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 377us/step - acc: 0.9914 - loss: 0.0258

 7178/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9914 - loss: 0.0258

 7310/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9914 - loss: 0.0259

 7444/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9914 - loss: 0.0259

 7580/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 378us/step - acc: 0.9914 - loss: 0.0260

 7718/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 377us/step - acc: 0.9914 - loss: 0.0260

 7851/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 377us/step - acc: 0.9914 - loss: 0.0260

 7989/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 377us/step - acc: 0.9914 - loss: 0.0261

 8131/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 377us/step - acc: 0.9914 - loss: 0.0261

 8270/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 376us/step - acc: 0.9914 - loss: 0.0262

 8413/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 376us/step - acc: 0.9914 - loss: 0.0262

 8554/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 376us/step - acc: 0.9914 - loss: 0.0263

 8695/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 375us/step - acc: 0.9914 - loss: 0.0263

 8834/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 375us/step - acc: 0.9913 - loss: 0.0264

 8970/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 375us/step - acc: 0.9913 - loss: 0.0264

 9112/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 375us/step - acc: 0.9913 - loss: 0.0264

 9252/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 374us/step - acc: 0.9913 - loss: 0.0265

 9379/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 375us/step - acc: 0.9913 - loss: 0.0265

 9511/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 375us/step - acc: 0.9913 - loss: 0.0266

 9652/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 375us/step - acc: 0.9913 - loss: 0.0266

 9786/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 375us/step - acc: 0.9913 - loss: 0.0267

 9925/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 374us/step - acc: 0.9912 - loss: 0.0267

10064/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 374us/step - acc: 0.9912 - loss: 0.0267

10200/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 374us/step - acc: 0.9912 - loss: 0.0268

10342/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 374us/step - acc: 0.9912 - loss: 0.0268

10482/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 374us/step - acc: 0.9912 - loss: 0.0268

10622/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 373us/step - acc: 0.9912 - loss: 0.0269

10764/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 373us/step - acc: 0.9912 - loss: 0.0269

10905/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 373us/step - acc: 0.9912 - loss: 0.0269

11047/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 373us/step - acc: 0.9912 - loss: 0.0270

11188/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 372us/step - acc: 0.9912 - loss: 0.0270

11329/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 372us/step - acc: 0.9912 - loss: 0.0270

11472/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 372us/step - acc: 0.9912 - loss: 0.0271

11615/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 372us/step - acc: 0.9912 - loss: 0.0271

11756/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 371us/step - acc: 0.9912 - loss: 0.0271

11896/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 371us/step - acc: 0.9911 - loss: 0.0272

12037/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 371us/step - acc: 0.9911 - loss: 0.0272

12179/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 371us/step - acc: 0.9911 - loss: 0.0272

12319/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 371us/step - acc: 0.9911 - loss: 0.0273

12463/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 371us/step - acc: 0.9911 - loss: 0.0273

12601/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 370us/step - acc: 0.9911 - loss: 0.0273

12736/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 370us/step - acc: 0.9911 - loss: 0.0273

12879/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 370us/step - acc: 0.9911 - loss: 0.0274

13021/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 370us/step - acc: 0.9911 - loss: 0.0274

13158/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 370us/step - acc: 0.9911 - loss: 0.0274

13298/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 370us/step - acc: 0.9911 - loss: 0.0274

13437/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 370us/step - acc: 0.9911 - loss: 0.0275

13577/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 370us/step - acc: 0.9911 - loss: 0.0275

13719/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 369us/step - acc: 0.9911 - loss: 0.0275

13860/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 369us/step - acc: 0.9911 - loss: 0.0275

13958/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 370us/step - acc: 0.9911 - loss: 0.0275

14020/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 372us/step - acc: 0.9911 - loss: 0.0276

14151/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 372us/step - acc: 0.9911 - loss: 0.0276

14285/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 372us/step - acc: 0.9910 - loss: 0.0276

14419/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 373us/step - acc: 0.9910 - loss: 0.0276

14561/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 372us/step - acc: 0.9910 - loss: 0.0277

14702/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 372us/step - acc: 0.9910 - loss: 0.0277

14843/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 372us/step - acc: 0.9910 - loss: 0.0277

14984/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 372us/step - acc: 0.9910 - loss: 0.0277

15127/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 372us/step - acc: 0.9910 - loss: 0.0278

15254/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 372us/step - acc: 0.9910 - loss: 0.0278

15369/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 372us/step - acc: 0.9910 - loss: 0.0278

15496/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 373us/step - acc: 0.9910 - loss: 0.0278

15616/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 373us/step - acc: 0.9910 - loss: 0.0279

15728/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 373us/step - acc: 0.9910 - loss: 0.0279

15816/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 375us/step - acc: 0.9910 - loss: 0.0279

15877/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 376us/step - acc: 0.9909 - loss: 0.0279

15991/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 377us/step - acc: 0.9909 - loss: 0.0279

16108/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 377us/step - acc: 0.9909 - loss: 0.0280

16229/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 377us/step - acc: 0.9909 - loss: 0.0280

16345/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 378us/step - acc: 0.9909 - loss: 0.0280

16466/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 378us/step - acc: 0.9909 - loss: 0.0280

16591/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 378us/step - acc: 0.9909 - loss: 0.0280

16720/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 378us/step - acc: 0.9909 - loss: 0.0281

16843/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 379us/step - acc: 0.9909 - loss: 0.0281

16952/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 379us/step - acc: 0.9909 - loss: 0.0281

17062/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 380us/step - acc: 0.9909 - loss: 0.0281

17161/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 380us/step - acc: 0.9909 - loss: 0.0281

17277/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 381us/step - acc: 0.9909 - loss: 0.0282

17396/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 381us/step - acc: 0.9909 - loss: 0.0282

17512/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 381us/step - acc: 0.9909 - loss: 0.0282

17630/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 382us/step - acc: 0.9909 - loss: 0.0282

17733/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 382us/step - acc: 0.9908 - loss: 0.0282

17854/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 382us/step - acc: 0.9908 - loss: 0.0282

17962/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 383us/step - acc: 0.9908 - loss: 0.0283

18026/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 384us/step - acc: 0.9908 - loss: 0.0283

18128/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 385us/step - acc: 0.9908 - loss: 0.0283

18228/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 386us/step - acc: 0.9908 - loss: 0.0283

18340/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 386us/step - acc: 0.9908 - loss: 0.0283

18447/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 386us/step - acc: 0.9908 - loss: 0.0283

18559/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 387us/step - acc: 0.9908 - loss: 0.0284

18671/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 387us/step - acc: 0.9908 - loss: 0.0284

18795/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 387us/step - acc: 0.9908 - loss: 0.0284

18920/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 387us/step - acc: 0.9908 - loss: 0.0284

19046/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 387us/step - acc: 0.9908 - loss: 0.0284

19171/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 388us/step - acc: 0.9908 - loss: 0.0285

19294/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 388us/step - acc: 0.9908 - loss: 0.0285

19398/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 388us/step - acc: 0.9908 - loss: 0.0285

19491/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 389us/step - acc: 0.9907 - loss: 0.0285

19603/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 389us/step - acc: 0.9907 - loss: 0.0286

19712/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 390us/step - acc: 0.9907 - loss: 0.0286

19826/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 390us/step - acc: 0.9907 - loss: 0.0286

19938/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 390us/step - acc: 0.9907 - loss: 0.0286

20054/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 391us/step - acc: 0.9907 - loss: 0.0287

20176/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 391us/step - acc: 0.9907 - loss: 0.0287

20277/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 391us/step - acc: 0.9907 - loss: 0.0287

20395/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 391us/step - acc: 0.9907 - loss: 0.0288

20511/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 392us/step - acc: 0.9907 - loss: 0.0288

20621/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 392us/step - acc: 0.9907 - loss: 0.0288

20733/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 392us/step - acc: 0.9906 - loss: 0.0288

20803/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 393us/step - acc: 0.9906 - loss: 0.0289

20912/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 394us/step - acc: 0.9906 - loss: 0.0289

21007/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 394us/step - acc: 0.9906 - loss: 0.0289

21100/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 395us/step - acc: 0.9906 - loss: 0.0289

21221/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 395us/step - acc: 0.9906 - loss: 0.0289

21335/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 395us/step - acc: 0.9906 - loss: 0.0290

21437/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 396us/step - acc: 0.9906 - loss: 0.0290

21519/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 397us/step - acc: 0.9906 - loss: 0.0290

21625/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 397us/step - acc: 0.9906 - loss: 0.0290

21747/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 397us/step - acc: 0.9906 - loss: 0.0291

21859/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 397us/step - acc: 0.9906 - loss: 0.0291

21977/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 398us/step - acc: 0.9906 - loss: 0.0291

22091/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 398us/step - acc: 0.9906 - loss: 0.0291

22178/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 398us/step - acc: 0.9906 - loss: 0.0291

22211/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 400us/step - acc: 0.9906 - loss: 0.0291

22256/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 402us/step - acc: 0.9905 - loss: 0.0292

22346/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 402us/step - acc: 0.9905 - loss: 0.0292

22435/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 403us/step - acc: 0.9905 - loss: 0.0292

22542/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 403us/step - acc: 0.9905 - loss: 0.0292

22655/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 403us/step - acc: 0.9905 - loss: 0.0292

22755/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 404us/step - acc: 0.9905 - loss: 0.0292

22850/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 404us/step - acc: 0.9905 - loss: 0.0293

22954/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 405us/step - acc: 0.9905 - loss: 0.0293

23074/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 405us/step - acc: 0.9905 - loss: 0.0293

23169/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 405us/step - acc: 0.9905 - loss: 0.0293

23237/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 406us/step - acc: 0.9905 - loss: 0.0293

23328/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 407us/step - acc: 0.9905 - loss: 0.0293

23418/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 407us/step - acc: 0.9905 - loss: 0.0293

23492/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 408us/step - acc: 0.9905 - loss: 0.0294

23594/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 409us/step - acc: 0.9905 - loss: 0.0294

23691/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 409us/step - acc: 0.9905 - loss: 0.0294

23760/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 410us/step - acc: 0.9905 - loss: 0.0294

23837/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 411us/step - acc: 0.9905 - loss: 0.0294

23887/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 412us/step - acc: 0.9905 - loss: 0.0294

23924/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 414us/step - acc: 0.9905 - loss: 0.0294

23971/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 415us/step - acc: 0.9905 - loss: 0.0294

24000/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 417us/step - acc: 0.9905 - loss: 0.0294

24058/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 418us/step - acc: 0.9905 - loss: 0.0294

24122/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 419us/step - acc: 0.9905 - loss: 0.0294

24174/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 420us/step - acc: 0.9905 - loss: 0.0295

24229/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 421us/step - acc: 0.9905 - loss: 0.0295

24291/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 422us/step - acc: 0.9905 - loss: 0.0295

24356/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 423us/step - acc: 0.9904 - loss: 0.0295

24433/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 424us/step - acc: 0.9904 - loss: 0.0295

24528/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 424us/step - acc: 0.9904 - loss: 0.0295

24593/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 425us/step - acc: 0.9904 - loss: 0.0295

24665/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 426us/step - acc: 0.9904 - loss: 0.0295

24697/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 427us/step - acc: 0.9904 - loss: 0.0295

24743/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 429us/step - acc: 0.9904 - loss: 0.0295

24777/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 430us/step - acc: 0.9904 - loss: 0.0295

24835/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 431us/step - acc: 0.9904 - loss: 0.0295

24914/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 432us/step - acc: 0.9904 - loss: 0.0296

24995/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 432us/step - acc: 0.9904 - loss: 0.0296

25072/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 433us/step - acc: 0.9904 - loss: 0.0296

25140/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 434us/step - acc: 0.9904 - loss: 0.0296

25220/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 435us/step - acc: 0.9904 - loss: 0.0296

25280/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 436us/step - acc: 0.9904 - loss: 0.0296

25334/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 437us/step - acc: 0.9904 - loss: 0.0296

25422/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 437us/step - acc: 0.9904 - loss: 0.0296

25508/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 438us/step - acc: 0.9904 - loss: 0.0296

25609/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 438us/step - acc: 0.9904 - loss: 0.0296

25728/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 438us/step - acc: 0.9904 - loss: 0.0297

25836/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 438us/step - acc: 0.9904 - loss: 0.0297

25899/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 439us/step - acc: 0.9904 - loss: 0.0297

25945/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 440us/step - acc: 0.9904 - loss: 0.0297

25998/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 441us/step - acc: 0.9904 - loss: 0.0297

26025/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 443us/step - acc: 0.9904 - loss: 0.0297

26034/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 444us/step - acc: 0.9904 - loss: 0.0297

26045/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 446us/step - acc: 0.9904 - loss: 0.0297

26053/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 448us/step - acc: 0.9904 - loss: 0.0297

26074/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 450us/step - acc: 0.9904 - loss: 0.0297

26102/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 451us/step - acc: 0.9904 - loss: 0.0297

26153/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 452us/step - acc: 0.9904 - loss: 0.0297

26187/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 454us/step - acc: 0.9904 - loss: 0.0297

26240/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 455us/step - acc: 0.9904 - loss: 0.0297

26283/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 456us/step - acc: 0.9904 - loss: 0.0297

26338/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 457us/step - acc: 0.9904 - loss: 0.0297

26395/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 458us/step - acc: 0.9904 - loss: 0.0297

26425/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 459us/step - acc: 0.9904 - loss: 0.0297

26468/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 461us/step - acc: 0.9904 - loss: 0.0297

26542/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 461us/step - acc: 0.9904 - loss: 0.0297

26647/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 461us/step - acc: 0.9904 - loss: 0.0297

26736/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 462us/step - acc: 0.9904 - loss: 0.0298

26792/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 463us/step - acc: 0.9904 - loss: 0.0298

26853/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 463us/step - acc: 0.9903 - loss: 0.0298

26898/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 464us/step - acc: 0.9903 - loss: 0.0298

27003/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 465us/step - acc: 0.9903 - loss: 0.0298

27102/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 465us/step - acc: 0.9903 - loss: 0.0298

27206/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 465us/step - acc: 0.9903 - loss: 0.0298

27240/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 466us/step - acc: 0.9903 - loss: 0.0298

27242/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 468us/step - acc: 0.9903 - loss: 0.0298

27263/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 470us/step - acc: 0.9903 - loss: 0.0298

27300/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 471us/step - acc: 0.9903 - loss: 0.0298

27311/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 473us/step - acc: 0.9903 - loss: 0.0298

27312/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 475us/step - acc: 0.9903 - loss: 0.0298

27317/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 477us/step - acc: 0.9903 - loss: 0.0298

27320/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 479us/step - acc: 0.9903 - loss: 0.0298

27373/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 480us/step - acc: 0.9903 - loss: 0.0298

27398/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 481us/step - acc: 0.9903 - loss: 0.0298

27454/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 482us/step - acc: 0.9903 - loss: 0.0298

27540/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 482us/step - acc: 0.9903 - loss: 0.0298

27652/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 482us/step - acc: 0.9903 - loss: 0.0298

27742/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 482us/step - acc: 0.9903 - loss: 0.0299

27851/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 482us/step - acc: 0.9903 - loss: 0.0299

27963/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 482us/step - acc: 0.9903 - loss: 0.0299

28073/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 482us/step - acc: 0.9903 - loss: 0.0299

28190/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 482us/step - acc: 0.9903 - loss: 0.0299

28302/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 482us/step - acc: 0.9903 - loss: 0.0299

28423/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 481us/step - acc: 0.9903 - loss: 0.0299

28556/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 481us/step - acc: 0.9903 - loss: 0.0299

28663/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 481us/step - acc: 0.9903 - loss: 0.0299

28726/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 482us/step - acc: 0.9903 - loss: 0.0299

28841/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 481us/step - acc: 0.9903 - loss: 0.0299

28951/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 481us/step - acc: 0.9903 - loss: 0.0300

29069/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 481us/step - acc: 0.9903 - loss: 0.0300

29173/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 481us/step - acc: 0.9903 - loss: 0.0300

29278/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 481us/step - acc: 0.9903 - loss: 0.0300

29392/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 481us/step - acc: 0.9903 - loss: 0.0300

29506/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 481us/step - acc: 0.9903 - loss: 0.0300

29634/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 480us/step - acc: 0.9903 - loss: 0.0300

29760/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 480us/step - acc: 0.9903 - loss: 0.0300

29800/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 482us/step - acc: 0.9903 - loss: 0.0300

29801/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 484us/step - acc: 0.9903 - loss: 0.0300

29845/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 485us/step - acc: 0.9903 - loss: 0.0300

29904/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 486us/step - acc: 0.9903 - loss: 0.0300

29992/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 486us/step - acc: 0.9903 - loss: 0.0301

30075/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 486us/step - acc: 0.9902 - loss: 0.0301

30170/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 486us/step - acc: 0.9902 - loss: 0.0301

30267/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 486us/step - acc: 0.9902 - loss: 0.0301

30337/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 487us/step - acc: 0.9902 - loss: 0.0301

30411/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 487us/step - acc: 0.9902 - loss: 0.0301

30491/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 488us/step - acc: 0.9902 - loss: 0.0301

30574/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 488us/step - acc: 0.9902 - loss: 0.0301

30678/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 488us/step - acc: 0.9902 - loss: 0.0301

30782/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 488us/step - acc: 0.9902 - loss: 0.0301

30895/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 488us/step - acc: 0.9902 - loss: 0.0301

30994/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 488us/step - acc: 0.9902 - loss: 0.0302

31072/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 488us/step - acc: 0.9902 - loss: 0.0302

31169/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 489us/step - acc: 0.9902 - loss: 0.0302

31274/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 489us/step - acc: 0.9902 - loss: 0.0302

31385/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 488us/step - acc: 0.9902 - loss: 0.0302

31497/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 488us/step - acc: 0.9902 - loss: 0.0302

31609/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 488us/step - acc: 0.9902 - loss: 0.0302

31728/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 488us/step - acc: 0.9902 - loss: 0.0302

31844/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 488us/step - acc: 0.9902 - loss: 0.0302

31955/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 488us/step - acc: 0.9902 - loss: 0.0303

32069/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 487us/step - acc: 0.9902 - loss: 0.0303

32181/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 487us/step - acc: 0.9902 - loss: 0.0303

32302/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 487us/step - acc: 0.9902 - loss: 0.0303

32426/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 487us/step - acc: 0.9902 - loss: 0.0303

32545/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 486us/step - acc: 0.9902 - loss: 0.0303

32664/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 486us/step - acc: 0.9902 - loss: 0.0303

32756/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 486us/step - acc: 0.9902 - loss: 0.0303

32855/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 486us/step - acc: 0.9902 - loss: 0.0303

32961/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 486us/step - acc: 0.9902 - loss: 0.0303

33073/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 486us/step - acc: 0.9902 - loss: 0.0304

33191/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 486us/step - acc: 0.9902 - loss: 0.0304

33288/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 486us/step - acc: 0.9901 - loss: 0.0304

33408/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 486us/step - acc: 0.9901 - loss: 0.0304

33526/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 486us/step - acc: 0.9901 - loss: 0.0304

33637/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 486us/step - acc: 0.9901 - loss: 0.0304

33748/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 485us/step - acc: 0.9901 - loss: 0.0304

33866/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 485us/step - acc: 0.9901 - loss: 0.0304

33971/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 485us/step - acc: 0.9901 - loss: 0.0304

34086/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 485us/step - acc: 0.9901 - loss: 0.0304

34217/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 485us/step - acc: 0.9901 - loss: 0.0304

34344/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 484us/step - acc: 0.9901 - loss: 0.0304

34439/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 484us/step - acc: 0.9901 - loss: 0.0304

34541/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 484us/step - acc: 0.9901 - loss: 0.0305

34662/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 484us/step - acc: 0.9901 - loss: 0.0305

34782/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 484us/step - acc: 0.9901 - loss: 0.0305

34905/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 484us/step - acc: 0.9901 - loss: 0.0305

35014/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 484us/step - acc: 0.9901 - loss: 0.0305

35134/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 483us/step - acc: 0.9901 - loss: 0.0305

35250/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 483us/step - acc: 0.9901 - loss: 0.0305

35367/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 483us/step - acc: 0.9901 - loss: 0.0305

35470/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 483us/step - acc: 0.9901 - loss: 0.0305

35557/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 483us/step - acc: 0.9901 - loss: 0.0305

35615/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 484us/step - acc: 0.9901 - loss: 0.0305

35722/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 484us/step - acc: 0.9901 - loss: 0.0305

35824/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 484us/step - acc: 0.9901 - loss: 0.0305

35931/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 484us/step - acc: 0.9901 - loss: 0.0305

36027/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 484us/step - acc: 0.9901 - loss: 0.0305

36144/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 484us/step - acc: 0.9901 - loss: 0.0306

36267/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 484us/step - acc: 0.9901 - loss: 0.0306

36359/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 484us/step - acc: 0.9901 - loss: 0.0306

36478/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 484us/step - acc: 0.9901 - loss: 0.0306

36596/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 483us/step - acc: 0.9901 - loss: 0.0306

36711/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 483us/step - acc: 0.9901 - loss: 0.0306

36832/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 483us/step - acc: 0.9901 - loss: 0.0306

36948/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 483us/step - acc: 0.9901 - loss: 0.0306

37077/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 482us/step - acc: 0.9901 - loss: 0.0306

37176/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 483us/step - acc: 0.9901 - loss: 0.0306

37295/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 482us/step - acc: 0.9901 - loss: 0.0306

37367/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 483us/step - acc: 0.9901 - loss: 0.0306

37466/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 483us/step - acc: 0.9901 - loss: 0.0306

37559/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 483us/step - acc: 0.9901 - loss: 0.0306

37661/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 483us/step - acc: 0.9901 - loss: 0.0306

37756/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 483us/step - acc: 0.9901 - loss: 0.0307

37841/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 483us/step - acc: 0.9901 - loss: 0.0307

37905/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 484us/step - acc: 0.9901 - loss: 0.0307

37982/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 484us/step - acc: 0.9901 - loss: 0.0307

38094/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 484us/step - acc: 0.9901 - loss: 0.0307

38210/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 484us/step - acc: 0.9901 - loss: 0.0307

38328/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 484us/step - acc: 0.9900 - loss: 0.0307

38446/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 484us/step - acc: 0.9900 - loss: 0.0307

38571/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 483us/step - acc: 0.9900 - loss: 0.0307

38696/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 483us/step - acc: 0.9900 - loss: 0.0307

38796/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 483us/step - acc: 0.9900 - loss: 0.0307

38812/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 484us/step - acc: 0.9900 - loss: 0.0307

38899/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 484us/step - acc: 0.9900 - loss: 0.0307

39024/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 484us/step - acc: 0.9900 - loss: 0.0307

39146/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 484us/step - acc: 0.9900 - loss: 0.0307

39274/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 484us/step - acc: 0.9900 - loss: 0.0307

39408/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 483us/step - acc: 0.9900 - loss: 0.0308 

39535/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 483us/step - acc: 0.9900 - loss: 0.0308

39657/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 483us/step - acc: 0.9900 - loss: 0.0308

39788/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 482us/step - acc: 0.9900 - loss: 0.0308

39897/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 482us/step - acc: 0.9900 - loss: 0.0308

40009/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 482us/step - acc: 0.9900 - loss: 0.0308

40105/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 482us/step - acc: 0.9900 - loss: 0.0308

40131/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 483us/step - acc: 0.9900 - loss: 0.0308

40200/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 484us/step - acc: 0.9900 - loss: 0.0308

40328/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 483us/step - acc: 0.9900 - loss: 0.0308

40460/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 483us/step - acc: 0.9900 - loss: 0.0308

40586/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 483us/step - acc: 0.9900 - loss: 0.0308

40713/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 483us/step - acc: 0.9900 - loss: 0.0308

40839/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 482us/step - acc: 0.9900 - loss: 0.0308

40971/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 482us/step - acc: 0.9900 - loss: 0.0308

41090/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 482us/step - acc: 0.9900 - loss: 0.0308

41204/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 482us/step - acc: 0.9900 - loss: 0.0308

41296/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 482us/step - acc: 0.9900 - loss: 0.0309

41352/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 482us/step - acc: 0.9900 - loss: 0.0309

41408/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 483us/step - acc: 0.9900 - loss: 0.0309

41475/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 484us/step - acc: 0.9900 - loss: 0.0309

41555/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 484us/step - acc: 0.9900 - loss: 0.0309

41591/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 485us/step - acc: 0.9900 - loss: 0.0309

41666/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 485us/step - acc: 0.9900 - loss: 0.0309

41762/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 485us/step - acc: 0.9900 - loss: 0.0309

41828/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 485us/step - acc: 0.9900 - loss: 0.0309

41945/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 485us/step - acc: 0.9900 - loss: 0.0309

42046/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 485us/step - acc: 0.9900 - loss: 0.0309

42106/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 486us/step - acc: 0.9900 - loss: 0.0309

42206/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 486us/step - acc: 0.9900 - loss: 0.0309

42312/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 486us/step - acc: 0.9900 - loss: 0.0309

42429/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 486us/step - acc: 0.9900 - loss: 0.0309

42540/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 486us/step - acc: 0.9900 - loss: 0.0309

42647/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 486us/step - acc: 0.9900 - loss: 0.0309

42744/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 486us/step - acc: 0.9900 - loss: 0.0309

42869/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 485us/step - acc: 0.9900 - loss: 0.0309

42990/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 485us/step - acc: 0.9900 - loss: 0.0309

43122/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 485us/step - acc: 0.9900 - loss: 0.0309

43259/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 484us/step - acc: 0.9900 - loss: 0.0309

43389/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 484us/step - acc: 0.9900 - loss: 0.0309

43522/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 484us/step - acc: 0.9900 - loss: 0.0310

43660/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 483us/step - acc: 0.9900 - loss: 0.0310

43786/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 483us/step - acc: 0.9900 - loss: 0.0310

43924/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 483us/step - acc: 0.9900 - loss: 0.0310

44057/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 483us/step - acc: 0.9900 - loss: 0.0310

44199/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 482us/step - acc: 0.9900 - loss: 0.0310

44337/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 482us/step - acc: 0.9900 - loss: 0.0310

44478/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 481us/step - acc: 0.9900 - loss: 0.0310

44598/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 481us/step - acc: 0.9900 - loss: 0.0310

44726/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 481us/step - acc: 0.9900 - loss: 0.0310

44848/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 481us/step - acc: 0.9900 - loss: 0.0310

44980/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 480us/step - acc: 0.9900 - loss: 0.0310

45118/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 480us/step - acc: 0.9900 - loss: 0.0310

45235/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 480us/step - acc: 0.9899 - loss: 0.0310

45363/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 480us/step - acc: 0.9899 - loss: 0.0310

45495/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 479us/step - acc: 0.9899 - loss: 0.0310

45622/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 479us/step - acc: 0.9899 - loss: 0.0310

45726/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 479us/step - acc: 0.9899 - loss: 0.0310

45846/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 479us/step - acc: 0.9899 - loss: 0.0310

45973/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 479us/step - acc: 0.9899 - loss: 0.0310

46093/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 479us/step - acc: 0.9899 - loss: 0.0310

46223/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 478us/step - acc: 0.9899 - loss: 0.0311

46355/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 478us/step - acc: 0.9899 - loss: 0.0311

46484/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 478us/step - acc: 0.9899 - loss: 0.0311

46598/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 478us/step - acc: 0.9899 - loss: 0.0311

46696/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 478us/step - acc: 0.9899 - loss: 0.0311

46797/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 478us/step - acc: 0.9899 - loss: 0.0311

46905/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 478us/step - acc: 0.9899 - loss: 0.0311

47012/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 478us/step - acc: 0.9899 - loss: 0.0311

47128/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 478us/step - acc: 0.9899 - loss: 0.0311

47235/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 478us/step - acc: 0.9899 - loss: 0.0311

47346/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 478us/step - acc: 0.9899 - loss: 0.0311

47441/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 478us/step - acc: 0.9899 - loss: 0.0311

47557/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 478us/step - acc: 0.9899 - loss: 0.0311

47663/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 478us/step - acc: 0.9899 - loss: 0.0311

47772/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 478us/step - acc: 0.9899 - loss: 0.0311

47875/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 478us/step - acc: 0.9899 - loss: 0.0311

47910/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 478us/step - acc: 0.9899 - loss: 0.0311

47964/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 479us/step - acc: 0.9899 - loss: 0.0311

48012/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 479us/step - acc: 0.9899 - loss: 0.0311

48081/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 480us/step - acc: 0.9899 - loss: 0.0311

48159/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 480us/step - acc: 0.9899 - loss: 0.0311

48231/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 480us/step - acc: 0.9899 - loss: 0.0311

48296/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 481us/step - acc: 0.9899 - loss: 0.0311

48378/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 481us/step - acc: 0.9899 - loss: 0.0311

48452/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 481us/step - acc: 0.9899 - loss: 0.0311

48541/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 481us/step - acc: 0.9899 - loss: 0.0311

48638/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 482us/step - acc: 0.9899 - loss: 0.0311

48735/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 482us/step - acc: 0.9899 - loss: 0.0311

48844/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 482us/step - acc: 0.9899 - loss: 0.0311

48958/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 481us/step - acc: 0.9899 - loss: 0.0311

49083/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 481us/step - acc: 0.9899 - loss: 0.0311

49200/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 481us/step - acc: 0.9899 - loss: 0.0311

49313/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 481us/step - acc: 0.9899 - loss: 0.0311

49336/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 482us/step - acc: 0.9899 - loss: 0.0311

49431/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 482us/step - acc: 0.9899 - loss: 0.0311

49534/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 482us/step - acc: 0.9899 - loss: 0.0311

49642/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 482us/step - acc: 0.9899 - loss: 0.0311

49741/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 482us/step - acc: 0.9899 - loss: 0.0311

49832/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 482us/step - acc: 0.9899 - loss: 0.0312

49935/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 482us/step - acc: 0.9899 - loss: 0.0312

50049/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 482us/step - acc: 0.9899 - loss: 0.0312

50152/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 482us/step - acc: 0.9899 - loss: 0.0312

50268/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 482us/step - acc: 0.9899 - loss: 0.0312

50388/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 482us/step - acc: 0.9899 - loss: 0.0312

50506/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 482us/step - acc: 0.9899 - loss: 0.0312

50628/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 481us/step - acc: 0.9899 - loss: 0.0312

50746/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 481us/step - acc: 0.9899 - loss: 0.0312

50858/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 481us/step - acc: 0.9899 - loss: 0.0312

50983/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 481us/step - acc: 0.9899 - loss: 0.0312

51106/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 481us/step - acc: 0.9899 - loss: 0.0312

51233/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 481us/step - acc: 0.9899 - loss: 0.0312

51351/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 481us/step - acc: 0.9899 - loss: 0.0312

51477/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 480us/step - acc: 0.9899 - loss: 0.0312

51594/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 480us/step - acc: 0.9899 - loss: 0.0312

51718/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 480us/step - acc: 0.9899 - loss: 0.0312

51844/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 480us/step - acc: 0.9899 - loss: 0.0312

51930/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 480us/step - acc: 0.9899 - loss: 0.0312

52027/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 480us/step - acc: 0.9899 - loss: 0.0312

52148/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 480us/step - acc: 0.9899 - loss: 0.0312

52261/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 480us/step - acc: 0.9899 - loss: 0.0312

52381/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 480us/step - acc: 0.9899 - loss: 0.0312

52507/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 480us/step - acc: 0.9899 - loss: 0.0312

52625/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 479us/step - acc: 0.9899 - loss: 0.0312

52713/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 480us/step - acc: 0.9899 - loss: 0.0312

52818/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 480us/step - acc: 0.9899 - loss: 0.0312

52929/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 480us/step - acc: 0.9899 - loss: 0.0312

53052/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 479us/step - acc: 0.9899 - loss: 0.0312

53175/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 479us/step - acc: 0.9899 - loss: 0.0312

53282/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 479us/step - acc: 0.9899 - loss: 0.0312

53358/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 479us/step - acc: 0.9899 - loss: 0.0312

53447/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 480us/step - acc: 0.9899 - loss: 0.0312

53542/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 480us/step - acc: 0.9899 - loss: 0.0312

53657/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 480us/step - acc: 0.9899 - loss: 0.0312

53776/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 479us/step - acc: 0.9899 - loss: 0.0312

53885/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 479us/step - acc: 0.9899 - loss: 0.0312

54001/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 479us/step - acc: 0.9899 - loss: 0.0313

54122/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 479us/step - acc: 0.9899 - loss: 0.0313

54233/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 479us/step - acc: 0.9899 - loss: 0.0313

54345/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 479us/step - acc: 0.9899 - loss: 0.0313

54462/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 479us/step - acc: 0.9899 - loss: 0.0313

54575/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 479us/step - acc: 0.9899 - loss: 0.0313

54679/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 479us/step - acc: 0.9899 - loss: 0.0313

54785/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 479us/step - acc: 0.9899 - loss: 0.0313

54908/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 479us/step - acc: 0.9899 - loss: 0.0313

55031/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 479us/step - acc: 0.9899 - loss: 0.0313

55156/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 478us/step - acc: 0.9899 - loss: 0.0313

55285/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 478us/step - acc: 0.9899 - loss: 0.0313

55417/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 478us/step - acc: 0.9898 - loss: 0.0313

55548/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 478us/step - acc: 0.9898 - loss: 0.0313

55680/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 478us/step - acc: 0.9898 - loss: 0.0313

55809/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 477us/step - acc: 0.9898 - loss: 0.0313

55942/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 477us/step - acc: 0.9898 - loss: 0.0313

56071/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 477us/step - acc: 0.9898 - loss: 0.0313

56197/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 477us/step - acc: 0.9898 - loss: 0.0313

56317/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 477us/step - acc: 0.9898 - loss: 0.0313

56439/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 476us/step - acc: 0.9898 - loss: 0.0313

56548/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 476us/step - acc: 0.9898 - loss: 0.0313

56668/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 476us/step - acc: 0.9898 - loss: 0.0313

56793/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 476us/step - acc: 0.9898 - loss: 0.0313

56924/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 476us/step - acc: 0.9898 - loss: 0.0313

57047/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 476us/step - acc: 0.9898 - loss: 0.0313

57172/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 476us/step - acc: 0.9898 - loss: 0.0314

57295/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 475us/step - acc: 0.9898 - loss: 0.0314

57412/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 475us/step - acc: 0.9898 - loss: 0.0314

57530/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 475us/step - acc: 0.9898 - loss: 0.0314

57653/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 475us/step - acc: 0.9898 - loss: 0.0314

57773/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 475us/step - acc: 0.9898 - loss: 0.0314

57905/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 475us/step - acc: 0.9898 - loss: 0.0314

58029/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 475us/step - acc: 0.9898 - loss: 0.0314

58158/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 474us/step - acc: 0.9898 - loss: 0.0314

58292/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 474us/step - acc: 0.9898 - loss: 0.0314

58425/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 474us/step - acc: 0.9898 - loss: 0.0314

58565/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 474us/step - acc: 0.9898 - loss: 0.0314

58705/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 473us/step - acc: 0.9898 - loss: 0.0314

58841/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 473us/step - acc: 0.9898 - loss: 0.0314

58975/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 473us/step - acc: 0.9898 - loss: 0.0314

59111/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 473us/step - acc: 0.9898 - loss: 0.0314

59249/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 472us/step - acc: 0.9898 - loss: 0.0314

59383/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 472us/step - acc: 0.9898 - loss: 0.0314

59523/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 472us/step - acc: 0.9898 - loss: 0.0314

59656/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 472us/step - acc: 0.9898 - loss: 0.0314

59789/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 472us/step - acc: 0.9898 - loss: 0.0314

59922/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 471us/step - acc: 0.9898 - loss: 0.0314

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 530us/step - acc: 0.9898 - loss: 0.0314 - val_acc: 0.9733 - val_loss: 0.1062

Epoch 15/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 8:59 9ms/step - acc: 1.0000 - loss: 0.0010

  129/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 391us/step - acc: 1.0000 - loss: 0.0017

  260/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 387us/step - acc: 0.9985 - loss: 0.0062

  380/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 397us/step - acc: 0.9980 - loss: 0.0076

  510/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 394us/step - acc: 0.9979 - loss: 0.0084

  645/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 390us/step - acc: 0.9979 - loss: 0.0086

  782/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 385us/step - acc: 0.9977 - loss: 0.0091

  918/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 383us/step - acc: 0.9975 - loss: 0.0098

 1056/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 380us/step - acc: 0.9973 - loss: 0.0104

 1192/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 379us/step - acc: 0.9972 - loss: 0.0107

 1330/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 378us/step - acc: 0.9971 - loss: 0.0111

 1467/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 376us/step - acc: 0.9969 - loss: 0.0115

 1604/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 376us/step - acc: 0.9967 - loss: 0.0121

 1739/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 375us/step - acc: 0.9965 - loss: 0.0127

 1878/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 374us/step - acc: 0.9963 - loss: 0.0132

 2014/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 374us/step - acc: 0.9961 - loss: 0.0136

 2152/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 373us/step - acc: 0.9959 - loss: 0.0140

 2287/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 373us/step - acc: 0.9957 - loss: 0.0142

 2423/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 373us/step - acc: 0.9956 - loss: 0.0146

 2559/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 373us/step - acc: 0.9954 - loss: 0.0150

 2699/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 372us/step - acc: 0.9951 - loss: 0.0153

 2834/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 372us/step - acc: 0.9949 - loss: 0.0157

 2974/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 371us/step - acc: 0.9948 - loss: 0.0160

 3111/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 371us/step - acc: 0.9946 - loss: 0.0163

 3249/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 371us/step - acc: 0.9945 - loss: 0.0165

 3386/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 370us/step - acc: 0.9944 - loss: 0.0168

 3524/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 370us/step - acc: 0.9943 - loss: 0.0169

 3657/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 370us/step - acc: 0.9942 - loss: 0.0171

 3791/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 371us/step - acc: 0.9941 - loss: 0.0173

 3923/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 371us/step - acc: 0.9940 - loss: 0.0175

 4051/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 372us/step - acc: 0.9939 - loss: 0.0177

 4188/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 371us/step - acc: 0.9938 - loss: 0.0179

 4326/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 371us/step - acc: 0.9938 - loss: 0.0180

 4466/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 371us/step - acc: 0.9937 - loss: 0.0182

 4604/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 371us/step - acc: 0.9936 - loss: 0.0184

 4741/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 370us/step - acc: 0.9935 - loss: 0.0185

 4879/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 370us/step - acc: 0.9935 - loss: 0.0186

 5014/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 370us/step - acc: 0.9934 - loss: 0.0187

 5152/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 370us/step - acc: 0.9934 - loss: 0.0189

 5290/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 370us/step - acc: 0.9933 - loss: 0.0190

 5427/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 370us/step - acc: 0.9932 - loss: 0.0191

 5566/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 370us/step - acc: 0.9932 - loss: 0.0193

 5705/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 369us/step - acc: 0.9931 - loss: 0.0194

 5842/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 369us/step - acc: 0.9931 - loss: 0.0195

 5980/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 369us/step - acc: 0.9930 - loss: 0.0196

 6119/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 369us/step - acc: 0.9930 - loss: 0.0196

 6259/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 369us/step - acc: 0.9929 - loss: 0.0197

 6394/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 369us/step - acc: 0.9929 - loss: 0.0198

 6533/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 369us/step - acc: 0.9929 - loss: 0.0199

 6673/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 368us/step - acc: 0.9928 - loss: 0.0200

 6807/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 369us/step - acc: 0.9928 - loss: 0.0201

 6944/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 369us/step - acc: 0.9928 - loss: 0.0202

 7078/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 369us/step - acc: 0.9928 - loss: 0.0202

 7216/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 369us/step - acc: 0.9927 - loss: 0.0203

 7353/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 369us/step - acc: 0.9927 - loss: 0.0203

 7493/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 368us/step - acc: 0.9927 - loss: 0.0204

 7628/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 368us/step - acc: 0.9927 - loss: 0.0205

 7763/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 368us/step - acc: 0.9926 - loss: 0.0205

 7900/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 368us/step - acc: 0.9926 - loss: 0.0206

 8037/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 368us/step - acc: 0.9926 - loss: 0.0206

 8174/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 368us/step - acc: 0.9926 - loss: 0.0206

 8310/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 368us/step - acc: 0.9926 - loss: 0.0207

 8443/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 368us/step - acc: 0.9926 - loss: 0.0207

 8578/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 369us/step - acc: 0.9926 - loss: 0.0208

 8713/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 369us/step - acc: 0.9926 - loss: 0.0208

 8852/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 368us/step - acc: 0.9926 - loss: 0.0208

 8992/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 368us/step - acc: 0.9925 - loss: 0.0209

 9131/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 368us/step - acc: 0.9925 - loss: 0.0209

 9265/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 368us/step - acc: 0.9925 - loss: 0.0209

 9402/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 368us/step - acc: 0.9925 - loss: 0.0210

 9542/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 368us/step - acc: 0.9925 - loss: 0.0210

 9676/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 368us/step - acc: 0.9925 - loss: 0.0210

 9810/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 368us/step - acc: 0.9925 - loss: 0.0210

 9948/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 368us/step - acc: 0.9925 - loss: 0.0210

10082/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 368us/step - acc: 0.9925 - loss: 0.0211

10221/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 368us/step - acc: 0.9925 - loss: 0.0211

10357/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 368us/step - acc: 0.9925 - loss: 0.0211

10493/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 368us/step - acc: 0.9925 - loss: 0.0211

10632/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 368us/step - acc: 0.9925 - loss: 0.0211

10768/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 368us/step - acc: 0.9925 - loss: 0.0211

10904/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 368us/step - acc: 0.9925 - loss: 0.0211

11040/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 368us/step - acc: 0.9925 - loss: 0.0211

11175/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 368us/step - acc: 0.9925 - loss: 0.0211

11312/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 368us/step - acc: 0.9925 - loss: 0.0211

11452/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 368us/step - acc: 0.9925 - loss: 0.0211

11592/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 368us/step - acc: 0.9925 - loss: 0.0211

11728/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 368us/step - acc: 0.9925 - loss: 0.0211

11861/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 368us/step - acc: 0.9925 - loss: 0.0211

11994/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 368us/step - acc: 0.9925 - loss: 0.0211

12130/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 368us/step - acc: 0.9925 - loss: 0.0211

12268/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 368us/step - acc: 0.9925 - loss: 0.0211

12387/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 369us/step - acc: 0.9925 - loss: 0.0212

12520/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 369us/step - acc: 0.9925 - loss: 0.0212

12657/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 369us/step - acc: 0.9925 - loss: 0.0212

12794/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 369us/step - acc: 0.9925 - loss: 0.0212

12928/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 369us/step - acc: 0.9925 - loss: 0.0212

13065/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 369us/step - acc: 0.9925 - loss: 0.0212

13204/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 369us/step - acc: 0.9925 - loss: 0.0212

13340/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 369us/step - acc: 0.9925 - loss: 0.0212

13478/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 369us/step - acc: 0.9925 - loss: 0.0212

13616/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 369us/step - acc: 0.9925 - loss: 0.0213

13752/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 369us/step - acc: 0.9925 - loss: 0.0213

13884/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9925 - loss: 0.0213

14010/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9925 - loss: 0.0213

14145/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9925 - loss: 0.0213

14281/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9925 - loss: 0.0213

14416/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9925 - loss: 0.0213

14547/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9925 - loss: 0.0213

14683/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9925 - loss: 0.0213

14820/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9925 - loss: 0.0214

14957/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9925 - loss: 0.0214

15092/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9925 - loss: 0.0214

15229/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9925 - loss: 0.0214

15368/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9925 - loss: 0.0214

15507/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9925 - loss: 0.0214

15646/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9925 - loss: 0.0214

15782/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9925 - loss: 0.0215

15919/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9925 - loss: 0.0215

16058/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9925 - loss: 0.0215

16196/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9924 - loss: 0.0215

16333/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9924 - loss: 0.0215

16469/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 369us/step - acc: 0.9924 - loss: 0.0216

16607/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0216

16738/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0216

16857/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0216

16982/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0216

17116/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0217

17250/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0217

17386/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0217

17526/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0217

17660/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0218

17799/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0218

17937/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0218

18076/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0218

18212/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0219

18350/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0219

18489/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0219

18622/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0219

18751/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0219

18881/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0220

19016/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0220

19153/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0220

19289/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 369us/step - acc: 0.9924 - loss: 0.0220

19427/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 369us/step - acc: 0.9924 - loss: 0.0220

19563/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 369us/step - acc: 0.9924 - loss: 0.0221

19696/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 369us/step - acc: 0.9924 - loss: 0.0221

19831/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 369us/step - acc: 0.9924 - loss: 0.0221

19967/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 369us/step - acc: 0.9924 - loss: 0.0221

20104/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 369us/step - acc: 0.9923 - loss: 0.0221

20242/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 369us/step - acc: 0.9923 - loss: 0.0222

20376/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 369us/step - acc: 0.9923 - loss: 0.0222

20512/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 369us/step - acc: 0.9923 - loss: 0.0222

20646/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 369us/step - acc: 0.9923 - loss: 0.0222

20744/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 370us/step - acc: 0.9923 - loss: 0.0222

20851/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 371us/step - acc: 0.9923 - loss: 0.0223

20981/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 371us/step - acc: 0.9923 - loss: 0.0223

21110/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 371us/step - acc: 0.9923 - loss: 0.0223

21234/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 371us/step - acc: 0.9923 - loss: 0.0223

21370/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 371us/step - acc: 0.9923 - loss: 0.0224

21497/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 371us/step - acc: 0.9923 - loss: 0.0224

21621/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 371us/step - acc: 0.9923 - loss: 0.0224

21741/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 372us/step - acc: 0.9923 - loss: 0.0224

21868/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 372us/step - acc: 0.9923 - loss: 0.0224

21989/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 372us/step - acc: 0.9923 - loss: 0.0224

22118/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 372us/step - acc: 0.9923 - loss: 0.0225

22247/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 372us/step - acc: 0.9923 - loss: 0.0225

22386/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9923 - loss: 0.0225

22524/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9923 - loss: 0.0225

22661/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9923 - loss: 0.0225

22799/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9923 - loss: 0.0226

22935/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9923 - loss: 0.0226

23070/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9923 - loss: 0.0226

23208/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9923 - loss: 0.0226

23343/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9923 - loss: 0.0226

23478/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9923 - loss: 0.0227

23616/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9922 - loss: 0.0227

23754/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9922 - loss: 0.0227

23888/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9922 - loss: 0.0227

24018/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9922 - loss: 0.0227

24154/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9922 - loss: 0.0227

24281/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9922 - loss: 0.0228

24417/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9922 - loss: 0.0228

24556/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9922 - loss: 0.0228

24690/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9922 - loss: 0.0228

24814/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9922 - loss: 0.0228

24942/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 372us/step - acc: 0.9922 - loss: 0.0228

25077/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9922 - loss: 0.0229

25209/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9922 - loss: 0.0229

25346/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9922 - loss: 0.0229

25483/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9922 - loss: 0.0229

25620/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9922 - loss: 0.0229

25757/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9922 - loss: 0.0229

25893/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9922 - loss: 0.0229

26032/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9922 - loss: 0.0230

26142/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9922 - loss: 0.0230

26280/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9922 - loss: 0.0230

26417/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9922 - loss: 0.0230

26551/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9922 - loss: 0.0230

26688/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9922 - loss: 0.0230

26828/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9922 - loss: 0.0230

26967/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9922 - loss: 0.0230

27103/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9922 - loss: 0.0231

27240/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9922 - loss: 0.0231

27365/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9921 - loss: 0.0231

27498/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9921 - loss: 0.0231

27628/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9921 - loss: 0.0231

27757/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 372us/step - acc: 0.9921 - loss: 0.0231

27888/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 372us/step - acc: 0.9921 - loss: 0.0231

28017/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 373us/step - acc: 0.9921 - loss: 0.0232

28154/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 372us/step - acc: 0.9921 - loss: 0.0232

28286/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 373us/step - acc: 0.9921 - loss: 0.0232

28424/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 372us/step - acc: 0.9921 - loss: 0.0232

28561/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 372us/step - acc: 0.9921 - loss: 0.0232

28697/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 372us/step - acc: 0.9921 - loss: 0.0232

28822/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 373us/step - acc: 0.9921 - loss: 0.0233

28949/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 373us/step - acc: 0.9921 - loss: 0.0233

29080/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 373us/step - acc: 0.9921 - loss: 0.0233

29210/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 373us/step - acc: 0.9921 - loss: 0.0233

29348/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 373us/step - acc: 0.9921 - loss: 0.0233

29482/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 373us/step - acc: 0.9921 - loss: 0.0233

29620/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 373us/step - acc: 0.9921 - loss: 0.0233

29759/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 373us/step - acc: 0.9921 - loss: 0.0234

29898/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 373us/step - acc: 0.9921 - loss: 0.0234

30038/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 372us/step - acc: 0.9921 - loss: 0.0234

30174/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 372us/step - acc: 0.9921 - loss: 0.0234

30313/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 372us/step - acc: 0.9920 - loss: 0.0234

30448/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 372us/step - acc: 0.9920 - loss: 0.0234

30588/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 372us/step - acc: 0.9920 - loss: 0.0234

30724/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 372us/step - acc: 0.9920 - loss: 0.0234

30857/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 372us/step - acc: 0.9920 - loss: 0.0235

30988/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 372us/step - acc: 0.9920 - loss: 0.0235

31126/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 372us/step - acc: 0.9920 - loss: 0.0235

31264/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 372us/step - acc: 0.9920 - loss: 0.0235

31404/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 372us/step - acc: 0.9920 - loss: 0.0235

31538/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 372us/step - acc: 0.9920 - loss: 0.0235

31675/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 372us/step - acc: 0.9920 - loss: 0.0235

31797/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 372us/step - acc: 0.9920 - loss: 0.0235

31918/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 373us/step - acc: 0.9920 - loss: 0.0236

32047/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 373us/step - acc: 0.9920 - loss: 0.0236

32185/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 373us/step - acc: 0.9920 - loss: 0.0236

32323/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 373us/step - acc: 0.9920 - loss: 0.0236

32458/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 373us/step - acc: 0.9920 - loss: 0.0236

32584/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 373us/step - acc: 0.9920 - loss: 0.0236

32707/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 373us/step - acc: 0.9920 - loss: 0.0236

32832/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 373us/step - acc: 0.9920 - loss: 0.0236

32962/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 373us/step - acc: 0.9920 - loss: 0.0237

33091/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 373us/step - acc: 0.9920 - loss: 0.0237

33215/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9920 - loss: 0.0237 

33349/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9920 - loss: 0.0237

33484/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9919 - loss: 0.0237

33621/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9919 - loss: 0.0237

33758/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9919 - loss: 0.0237

33895/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9919 - loss: 0.0237

34032/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9919 - loss: 0.0238

34170/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9919 - loss: 0.0238

34309/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9919 - loss: 0.0238

34436/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9919 - loss: 0.0238

34574/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9919 - loss: 0.0238

34708/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9919 - loss: 0.0238

34842/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9919 - loss: 0.0238

34978/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9919 - loss: 0.0239

35116/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9919 - loss: 0.0239

35240/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9919 - loss: 0.0239

35370/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9919 - loss: 0.0239

35506/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9919 - loss: 0.0239

35644/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9919 - loss: 0.0239

35777/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 373us/step - acc: 0.9919 - loss: 0.0239

35913/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9919 - loss: 0.0240

36049/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9919 - loss: 0.0240

36184/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9919 - loss: 0.0240

36318/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9919 - loss: 0.0240

36452/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9919 - loss: 0.0240

36589/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9918 - loss: 0.0240

36727/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9918 - loss: 0.0241

36865/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9918 - loss: 0.0241

36996/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9918 - loss: 0.0241

37130/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9918 - loss: 0.0241

37267/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9918 - loss: 0.0241

37403/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9918 - loss: 0.0241

37539/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9918 - loss: 0.0241

37677/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9918 - loss: 0.0242

37814/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9918 - loss: 0.0242

37952/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9918 - loss: 0.0242

38090/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9918 - loss: 0.0242

38224/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9918 - loss: 0.0242

38358/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9918 - loss: 0.0242

38496/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 373us/step - acc: 0.9918 - loss: 0.0243

38633/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9918 - loss: 0.0243

38770/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9918 - loss: 0.0243

38907/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9918 - loss: 0.0243

39039/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9918 - loss: 0.0243

39173/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9918 - loss: 0.0243

39309/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9918 - loss: 0.0243

39448/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9917 - loss: 0.0244

39584/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9917 - loss: 0.0244

39722/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9917 - loss: 0.0244

39859/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9917 - loss: 0.0244

39996/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9917 - loss: 0.0244

40130/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9917 - loss: 0.0244

40267/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9917 - loss: 0.0245

40405/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9917 - loss: 0.0245

40541/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9917 - loss: 0.0245

40666/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9917 - loss: 0.0245

40798/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9917 - loss: 0.0245

40933/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9917 - loss: 0.0245

41069/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9917 - loss: 0.0245

41202/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 373us/step - acc: 0.9917 - loss: 0.0246

41341/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9917 - loss: 0.0246

41476/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9917 - loss: 0.0246

41612/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9917 - loss: 0.0246

41748/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9917 - loss: 0.0246

41885/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9917 - loss: 0.0246

42023/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9917 - loss: 0.0247

42160/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9917 - loss: 0.0247

42294/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9917 - loss: 0.0247

42432/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9916 - loss: 0.0247

42556/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9916 - loss: 0.0247

42690/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9916 - loss: 0.0247

42829/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9916 - loss: 0.0247

42964/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9916 - loss: 0.0248

43103/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9916 - loss: 0.0248

43244/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9916 - loss: 0.0248

43371/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9916 - loss: 0.0248

43507/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9916 - loss: 0.0248

43642/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9916 - loss: 0.0248

43780/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 373us/step - acc: 0.9916 - loss: 0.0248

43915/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9916 - loss: 0.0249

44041/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9916 - loss: 0.0249

44148/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9916 - loss: 0.0249

44265/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9916 - loss: 0.0249

44390/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9916 - loss: 0.0249

44507/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9916 - loss: 0.0249

44633/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9916 - loss: 0.0249

44752/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9916 - loss: 0.0249

44881/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 373us/step - acc: 0.9916 - loss: 0.0249

45006/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 374us/step - acc: 0.9916 - loss: 0.0250

45127/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 374us/step - acc: 0.9916 - loss: 0.0250

45247/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 374us/step - acc: 0.9916 - loss: 0.0250

45370/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 374us/step - acc: 0.9916 - loss: 0.0250

45490/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 374us/step - acc: 0.9916 - loss: 0.0250

45615/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 374us/step - acc: 0.9916 - loss: 0.0250

45729/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 374us/step - acc: 0.9915 - loss: 0.0250

45840/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 374us/step - acc: 0.9915 - loss: 0.0250

45953/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 375us/step - acc: 0.9915 - loss: 0.0251

46062/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 375us/step - acc: 0.9915 - loss: 0.0251

46174/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 375us/step - acc: 0.9915 - loss: 0.0251

46281/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 375us/step - acc: 0.9915 - loss: 0.0251

46395/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 375us/step - acc: 0.9915 - loss: 0.0251

46513/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 375us/step - acc: 0.9915 - loss: 0.0251

46634/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 376us/step - acc: 0.9915 - loss: 0.0251

46760/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 376us/step - acc: 0.9915 - loss: 0.0251

46878/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 376us/step - acc: 0.9915 - loss: 0.0251

47002/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 376us/step - acc: 0.9915 - loss: 0.0251

47128/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 376us/step - acc: 0.9915 - loss: 0.0252

47254/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 376us/step - acc: 0.9915 - loss: 0.0252

47375/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 376us/step - acc: 0.9915 - loss: 0.0252

47492/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 376us/step - acc: 0.9915 - loss: 0.0252

47616/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 376us/step - acc: 0.9915 - loss: 0.0252

47738/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 376us/step - acc: 0.9915 - loss: 0.0252

47854/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 376us/step - acc: 0.9915 - loss: 0.0252

47980/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 377us/step - acc: 0.9915 - loss: 0.0252

48098/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 377us/step - acc: 0.9915 - loss: 0.0252

48175/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 377us/step - acc: 0.9915 - loss: 0.0252

48292/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 377us/step - acc: 0.9915 - loss: 0.0252

48413/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 377us/step - acc: 0.9915 - loss: 0.0253

48534/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 377us/step - acc: 0.9915 - loss: 0.0253

48650/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 378us/step - acc: 0.9915 - loss: 0.0253

48754/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 378us/step - acc: 0.9915 - loss: 0.0253

48873/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 378us/step - acc: 0.9915 - loss: 0.0253

48989/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 378us/step - acc: 0.9915 - loss: 0.0253

49104/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 378us/step - acc: 0.9915 - loss: 0.0253

49220/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 378us/step - acc: 0.9915 - loss: 0.0253

49345/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 378us/step - acc: 0.9915 - loss: 0.0253

49466/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 378us/step - acc: 0.9915 - loss: 0.0253

49581/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 379us/step - acc: 0.9915 - loss: 0.0253

49703/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 379us/step - acc: 0.9915 - loss: 0.0253

49804/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 379us/step - acc: 0.9915 - loss: 0.0253

49904/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 379us/step - acc: 0.9915 - loss: 0.0254

50003/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 379us/step - acc: 0.9914 - loss: 0.0254

50104/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 380us/step - acc: 0.9914 - loss: 0.0254

50206/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 380us/step - acc: 0.9914 - loss: 0.0254

50305/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 380us/step - acc: 0.9914 - loss: 0.0254

50413/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 380us/step - acc: 0.9914 - loss: 0.0254

50477/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 381us/step - acc: 0.9914 - loss: 0.0254

50594/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 381us/step - acc: 0.9914 - loss: 0.0254

50704/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 381us/step - acc: 0.9914 - loss: 0.0254

50818/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 381us/step - acc: 0.9914 - loss: 0.0254

50922/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 381us/step - acc: 0.9914 - loss: 0.0254

51036/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9914 - loss: 0.0254

51148/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9914 - loss: 0.0254

51261/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9914 - loss: 0.0254

51368/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9914 - loss: 0.0254

51455/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 382us/step - acc: 0.9914 - loss: 0.0255

51547/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9914 - loss: 0.0255

51604/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 383us/step - acc: 0.9914 - loss: 0.0255

51686/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 384us/step - acc: 0.9914 - loss: 0.0255

51779/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 384us/step - acc: 0.9914 - loss: 0.0255

51876/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 384us/step - acc: 0.9914 - loss: 0.0255

51980/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 384us/step - acc: 0.9914 - loss: 0.0255

52059/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 385us/step - acc: 0.9914 - loss: 0.0255

52138/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 385us/step - acc: 0.9914 - loss: 0.0255

52218/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 385us/step - acc: 0.9914 - loss: 0.0255

52328/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9914 - loss: 0.0255

52449/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9914 - loss: 0.0255

52560/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9914 - loss: 0.0255

52680/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9914 - loss: 0.0255

52792/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9914 - loss: 0.0255

52920/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9914 - loss: 0.0255

53040/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9914 - loss: 0.0256

53166/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9914 - loss: 0.0256

53284/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9914 - loss: 0.0256

53410/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9914 - loss: 0.0256

53540/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9914 - loss: 0.0256

53661/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9914 - loss: 0.0256

53775/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 386us/step - acc: 0.9914 - loss: 0.0256

53878/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 387us/step - acc: 0.9914 - loss: 0.0256

53995/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 387us/step - acc: 0.9914 - loss: 0.0256

54115/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 387us/step - acc: 0.9914 - loss: 0.0256

54237/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 387us/step - acc: 0.9914 - loss: 0.0256

54350/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 387us/step - acc: 0.9914 - loss: 0.0256

54469/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 387us/step - acc: 0.9914 - loss: 0.0256

54554/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 387us/step - acc: 0.9914 - loss: 0.0257

54652/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 388us/step - acc: 0.9914 - loss: 0.0257

54771/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 388us/step - acc: 0.9914 - loss: 0.0257

54878/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 388us/step - acc: 0.9914 - loss: 0.0257

54969/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 388us/step - acc: 0.9914 - loss: 0.0257

55085/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 388us/step - acc: 0.9913 - loss: 0.0257

55207/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 388us/step - acc: 0.9913 - loss: 0.0257

55322/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 388us/step - acc: 0.9913 - loss: 0.0257

55429/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 389us/step - acc: 0.9913 - loss: 0.0257

55528/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 389us/step - acc: 0.9913 - loss: 0.0257

55631/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 389us/step - acc: 0.9913 - loss: 0.0257

55729/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 389us/step - acc: 0.9913 - loss: 0.0257

55851/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 389us/step - acc: 0.9913 - loss: 0.0257

55968/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 389us/step - acc: 0.9913 - loss: 0.0257

56086/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 389us/step - acc: 0.9913 - loss: 0.0257

56174/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 390us/step - acc: 0.9913 - loss: 0.0257

56291/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 390us/step - acc: 0.9913 - loss: 0.0258

56417/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 390us/step - acc: 0.9913 - loss: 0.0258

56535/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 390us/step - acc: 0.9913 - loss: 0.0258

56627/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 390us/step - acc: 0.9913 - loss: 0.0258

56649/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 391us/step - acc: 0.9913 - loss: 0.0258

56660/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 392us/step - acc: 0.9913 - loss: 0.0258

56674/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 392us/step - acc: 0.9913 - loss: 0.0258

56686/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 393us/step - acc: 0.9913 - loss: 0.0258

56701/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 394us/step - acc: 0.9913 - loss: 0.0258

56727/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 395us/step - acc: 0.9913 - loss: 0.0258

56775/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 396us/step - acc: 0.9913 - loss: 0.0258

56886/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 396us/step - acc: 0.9913 - loss: 0.0258

56985/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 396us/step - acc: 0.9913 - loss: 0.0258

57105/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 396us/step - acc: 0.9913 - loss: 0.0258

57228/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 396us/step - acc: 0.9913 - loss: 0.0258

57341/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 396us/step - acc: 0.9913 - loss: 0.0258

57462/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 396us/step - acc: 0.9913 - loss: 0.0258

57580/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 396us/step - acc: 0.9913 - loss: 0.0258

57696/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 396us/step - acc: 0.9913 - loss: 0.0258

57811/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 396us/step - acc: 0.9913 - loss: 0.0258

57931/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 396us/step - acc: 0.9913 - loss: 0.0258

58050/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 396us/step - acc: 0.9913 - loss: 0.0259

58167/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 396us/step - acc: 0.9913 - loss: 0.0259

58274/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9913 - loss: 0.0259

58383/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9913 - loss: 0.0259

58492/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9913 - loss: 0.0259

58611/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9913 - loss: 0.0259

58734/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9913 - loss: 0.0259

58850/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9913 - loss: 0.0259

58969/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9913 - loss: 0.0259

59093/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9913 - loss: 0.0259

59204/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9913 - loss: 0.0259

59319/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9913 - loss: 0.0259

59430/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9913 - loss: 0.0259

59535/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9913 - loss: 0.0259

59646/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 398us/step - acc: 0.9913 - loss: 0.0259

59770/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 398us/step - acc: 0.9913 - loss: 0.0260

59903/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9913 - loss: 0.0260

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 458us/step - acc: 0.9913 - loss: 0.0260 - val_acc: 0.9713 - val_loss: 0.1090

Epoch 16/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 11:47 12ms/step - acc: 1.0000 - loss: 5.9604e-06

  133/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 379us/step - acc: 1.0000 - loss: 0.0213     

  270/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 373us/step - acc: 0.9982 - loss: 0.0192

  393/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 384us/step - acc: 0.9969 - loss: 0.0189

  513/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 392us/step - acc: 0.9963 - loss: 0.0185

  642/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 391us/step - acc: 0.9959 - loss: 0.0184

  766/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 393us/step - acc: 0.9956 - loss: 0.0183

  893/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 394us/step - acc: 0.9956 - loss: 0.0181

 1010/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 398us/step - acc: 0.9953 - loss: 0.0185

 1132/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 399us/step - acc: 0.9951 - loss: 0.0191

 1255/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 400us/step - acc: 0.9949 - loss: 0.0196

 1377/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 401us/step - acc: 0.9948 - loss: 0.0199

 1497/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 402us/step - acc: 0.9947 - loss: 0.0202

 1614/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 404us/step - acc: 0.9946 - loss: 0.0204

 1719/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 409us/step - acc: 0.9945 - loss: 0.0206

 1838/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 410us/step - acc: 0.9945 - loss: 0.0207

 1952/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 412us/step - acc: 0.9944 - loss: 0.0209

 2066/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 414us/step - acc: 0.9944 - loss: 0.0211

 2185/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 414us/step - acc: 0.9943 - loss: 0.0213

 2302/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 415us/step - acc: 0.9942 - loss: 0.0214

 2410/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 417us/step - acc: 0.9941 - loss: 0.0215

 2525/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 418us/step - acc: 0.9940 - loss: 0.0217

 2636/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 419us/step - acc: 0.9939 - loss: 0.0219

 2761/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 419us/step - acc: 0.9938 - loss: 0.0223

 2879/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 419us/step - acc: 0.9937 - loss: 0.0225

 3001/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 419us/step - acc: 0.9936 - loss: 0.0227

 3122/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 418us/step - acc: 0.9935 - loss: 0.0230

 3245/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 418us/step - acc: 0.9934 - loss: 0.0231

 3345/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 421us/step - acc: 0.9934 - loss: 0.0232

 3440/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 424us/step - acc: 0.9933 - loss: 0.0234

 3550/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 425us/step - acc: 0.9933 - loss: 0.0235

 3666/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 425us/step - acc: 0.9932 - loss: 0.0237

 3755/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 428us/step - acc: 0.9931 - loss: 0.0238

 3824/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 434us/step - acc: 0.9931 - loss: 0.0239

 3912/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 437us/step - acc: 0.9930 - loss: 0.0240

 4011/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 439us/step - acc: 0.9929 - loss: 0.0241

 4122/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 439us/step - acc: 0.9929 - loss: 0.0242

 4232/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 439us/step - acc: 0.9929 - loss: 0.0243

 4350/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 439us/step - acc: 0.9928 - loss: 0.0244

 4473/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 438us/step - acc: 0.9928 - loss: 0.0245

 4595/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 437us/step - acc: 0.9927 - loss: 0.0245

 4717/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 437us/step - acc: 0.9927 - loss: 0.0245

 4832/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 437us/step - acc: 0.9927 - loss: 0.0246

 4942/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 437us/step - acc: 0.9927 - loss: 0.0246

 5054/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 438us/step - acc: 0.9927 - loss: 0.0246

 5168/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 438us/step - acc: 0.9926 - loss: 0.0246

 5289/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 437us/step - acc: 0.9926 - loss: 0.0246

 5415/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 436us/step - acc: 0.9926 - loss: 0.0246

 5535/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 436us/step - acc: 0.9926 - loss: 0.0246

 5656/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 435us/step - acc: 0.9925 - loss: 0.0246

 5777/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 435us/step - acc: 0.9925 - loss: 0.0246

 5893/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 435us/step - acc: 0.9925 - loss: 0.0246

 6003/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 435us/step - acc: 0.9925 - loss: 0.0246

 6093/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 437us/step - acc: 0.9924 - loss: 0.0246

 6190/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 438us/step - acc: 0.9924 - loss: 0.0246

 6239/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 443us/step - acc: 0.9924 - loss: 0.0246

 6330/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 445us/step - acc: 0.9924 - loss: 0.0246

 6425/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 446us/step - acc: 0.9924 - loss: 0.0246

 6542/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 446us/step - acc: 0.9924 - loss: 0.0246

 6647/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 446us/step - acc: 0.9923 - loss: 0.0246

 6753/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 446us/step - acc: 0.9923 - loss: 0.0246

 6860/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 447us/step - acc: 0.9923 - loss: 0.0246

 6953/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 448us/step - acc: 0.9923 - loss: 0.0246

 7068/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 448us/step - acc: 0.9923 - loss: 0.0246

 7188/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 447us/step - acc: 0.9923 - loss: 0.0246

 7289/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 448us/step - acc: 0.9922 - loss: 0.0246

 7399/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 448us/step - acc: 0.9922 - loss: 0.0246

 7514/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 448us/step - acc: 0.9922 - loss: 0.0246

 7641/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 447us/step - acc: 0.9922 - loss: 0.0246

 7741/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 448us/step - acc: 0.9922 - loss: 0.0247

 7827/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 449us/step - acc: 0.9922 - loss: 0.0247

 7937/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 450us/step - acc: 0.9921 - loss: 0.0247

 8022/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 451us/step - acc: 0.9921 - loss: 0.0247

 8108/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 452us/step - acc: 0.9921 - loss: 0.0247

 8225/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 452us/step - acc: 0.9921 - loss: 0.0247

 8322/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 453us/step - acc: 0.9921 - loss: 0.0248

 8410/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 454us/step - acc: 0.9921 - loss: 0.0248

 8505/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 455us/step - acc: 0.9921 - loss: 0.0248

 8603/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 456us/step - acc: 0.9921 - loss: 0.0248

 8710/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 456us/step - acc: 0.9920 - loss: 0.0248

 8829/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 455us/step - acc: 0.9920 - loss: 0.0248

 8957/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 455us/step - acc: 0.9920 - loss: 0.0248

 9048/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 456us/step - acc: 0.9920 - loss: 0.0249

 9163/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 455us/step - acc: 0.9920 - loss: 0.0249

 9262/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 456us/step - acc: 0.9920 - loss: 0.0249

 9378/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 456us/step - acc: 0.9920 - loss: 0.0249

 9479/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 456us/step - acc: 0.9920 - loss: 0.0249

 9593/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 456us/step - acc: 0.9920 - loss: 0.0249

 9714/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 455us/step - acc: 0.9920 - loss: 0.0249

 9838/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 455us/step - acc: 0.9920 - loss: 0.0249

 9922/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 456us/step - acc: 0.9920 - loss: 0.0250

10035/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 456us/step - acc: 0.9919 - loss: 0.0250

10151/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 456us/step - acc: 0.9919 - loss: 0.0250

10274/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 455us/step - acc: 0.9919 - loss: 0.0250

10381/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 455us/step - acc: 0.9919 - loss: 0.0250

10463/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 456us/step - acc: 0.9919 - loss: 0.0251

10558/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 457us/step - acc: 0.9919 - loss: 0.0251

10680/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 457us/step - acc: 0.9919 - loss: 0.0251

10797/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 456us/step - acc: 0.9919 - loss: 0.0251

10916/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 456us/step - acc: 0.9919 - loss: 0.0252

11039/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 455us/step - acc: 0.9919 - loss: 0.0252

11164/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 455us/step - acc: 0.9919 - loss: 0.0252

11289/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 454us/step - acc: 0.9918 - loss: 0.0253

11412/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 454us/step - acc: 0.9918 - loss: 0.0253

11539/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 453us/step - acc: 0.9918 - loss: 0.0253

11662/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 453us/step - acc: 0.9918 - loss: 0.0254

11785/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 452us/step - acc: 0.9918 - loss: 0.0254

11911/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 452us/step - acc: 0.9918 - loss: 0.0254

12033/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 451us/step - acc: 0.9918 - loss: 0.0255

12154/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 451us/step - acc: 0.9918 - loss: 0.0255

12284/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 450us/step - acc: 0.9918 - loss: 0.0255

12410/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 450us/step - acc: 0.9917 - loss: 0.0256

12529/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 449us/step - acc: 0.9917 - loss: 0.0256

12647/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 449us/step - acc: 0.9917 - loss: 0.0256

12783/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 448us/step - acc: 0.9917 - loss: 0.0257

12918/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 447us/step - acc: 0.9917 - loss: 0.0257

13054/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 447us/step - acc: 0.9917 - loss: 0.0258

13188/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 446us/step - acc: 0.9917 - loss: 0.0258

13236/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 448us/step - acc: 0.9917 - loss: 0.0258

13274/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 451us/step - acc: 0.9917 - loss: 0.0258

13372/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 451us/step - acc: 0.9917 - loss: 0.0259

13499/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 451us/step - acc: 0.9916 - loss: 0.0259

13634/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 450us/step - acc: 0.9916 - loss: 0.0259

13771/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 449us/step - acc: 0.9916 - loss: 0.0260

13906/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 448us/step - acc: 0.9916 - loss: 0.0260

14024/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 448us/step - acc: 0.9916 - loss: 0.0260

14157/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 447us/step - acc: 0.9916 - loss: 0.0261

14289/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 447us/step - acc: 0.9916 - loss: 0.0261

14416/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 446us/step - acc: 0.9916 - loss: 0.0261

14548/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 446us/step - acc: 0.9916 - loss: 0.0261

14680/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 445us/step - acc: 0.9916 - loss: 0.0261

14816/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 444us/step - acc: 0.9916 - loss: 0.0262

14940/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 444us/step - acc: 0.9916 - loss: 0.0262

15057/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 444us/step - acc: 0.9916 - loss: 0.0262

15192/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 443us/step - acc: 0.9915 - loss: 0.0262

15331/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 443us/step - acc: 0.9915 - loss: 0.0263

15462/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 442us/step - acc: 0.9915 - loss: 0.0263

15589/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 442us/step - acc: 0.9915 - loss: 0.0263

15724/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 441us/step - acc: 0.9915 - loss: 0.0263

15859/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 441us/step - acc: 0.9915 - loss: 0.0263

15981/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 440us/step - acc: 0.9915 - loss: 0.0263

16118/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 440us/step - acc: 0.9915 - loss: 0.0264

16256/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 439us/step - acc: 0.9915 - loss: 0.0264

16392/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 438us/step - acc: 0.9915 - loss: 0.0264

16529/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 438us/step - acc: 0.9915 - loss: 0.0264

16667/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 437us/step - acc: 0.9915 - loss: 0.0264

16793/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 437us/step - acc: 0.9915 - loss: 0.0264

16913/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 437us/step - acc: 0.9915 - loss: 0.0265

17040/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 436us/step - acc: 0.9915 - loss: 0.0265

17160/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 436us/step - acc: 0.9915 - loss: 0.0265

17288/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 436us/step - acc: 0.9915 - loss: 0.0265

17413/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 436us/step - acc: 0.9915 - loss: 0.0265

17538/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 436us/step - acc: 0.9915 - loss: 0.0265

17669/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 435us/step - acc: 0.9914 - loss: 0.0265

17805/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 435us/step - acc: 0.9914 - loss: 0.0266

17942/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 434us/step - acc: 0.9914 - loss: 0.0266

18079/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 434us/step - acc: 0.9914 - loss: 0.0266

18214/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 433us/step - acc: 0.9914 - loss: 0.0266

18348/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 433us/step - acc: 0.9914 - loss: 0.0266

18484/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 432us/step - acc: 0.9914 - loss: 0.0266

18618/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 432us/step - acc: 0.9914 - loss: 0.0266

18757/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 431us/step - acc: 0.9914 - loss: 0.0266

18894/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 431us/step - acc: 0.9914 - loss: 0.0266

19031/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 430us/step - acc: 0.9914 - loss: 0.0266

19161/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 430us/step - acc: 0.9914 - loss: 0.0267

19292/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 430us/step - acc: 0.9914 - loss: 0.0267

19420/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 430us/step - acc: 0.9914 - loss: 0.0267

19550/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 429us/step - acc: 0.9914 - loss: 0.0267

19686/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 429us/step - acc: 0.9914 - loss: 0.0267

19816/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 429us/step - acc: 0.9914 - loss: 0.0267

19947/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 428us/step - acc: 0.9914 - loss: 0.0267

20081/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 428us/step - acc: 0.9914 - loss: 0.0267

20206/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 428us/step - acc: 0.9914 - loss: 0.0267

20334/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 428us/step - acc: 0.9914 - loss: 0.0267

20471/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 427us/step - acc: 0.9914 - loss: 0.0267

20604/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 427us/step - acc: 0.9914 - loss: 0.0267

20731/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 427us/step - acc: 0.9914 - loss: 0.0267

20858/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 426us/step - acc: 0.9914 - loss: 0.0267

20994/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 426us/step - acc: 0.9914 - loss: 0.0267

21133/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 426us/step - acc: 0.9914 - loss: 0.0267

21265/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 425us/step - acc: 0.9914 - loss: 0.0268

21398/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 425us/step - acc: 0.9914 - loss: 0.0268

21530/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 425us/step - acc: 0.9914 - loss: 0.0268

21662/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 424us/step - acc: 0.9914 - loss: 0.0268

21795/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 424us/step - acc: 0.9914 - loss: 0.0268

21926/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 424us/step - acc: 0.9914 - loss: 0.0268

22061/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 424us/step - acc: 0.9914 - loss: 0.0268

22199/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 423us/step - acc: 0.9914 - loss: 0.0268

22328/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 423us/step - acc: 0.9914 - loss: 0.0268

22467/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 423us/step - acc: 0.9914 - loss: 0.0268

22605/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 422us/step - acc: 0.9914 - loss: 0.0268

22739/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 422us/step - acc: 0.9914 - loss: 0.0268

22877/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 422us/step - acc: 0.9914 - loss: 0.0268

23015/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 421us/step - acc: 0.9913 - loss: 0.0268

23151/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 421us/step - acc: 0.9913 - loss: 0.0268

23286/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 421us/step - acc: 0.9913 - loss: 0.0268

23422/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 420us/step - acc: 0.9913 - loss: 0.0269

23554/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 420us/step - acc: 0.9913 - loss: 0.0269

23690/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 420us/step - acc: 0.9913 - loss: 0.0269

23824/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 420us/step - acc: 0.9913 - loss: 0.0269

23954/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 419us/step - acc: 0.9913 - loss: 0.0269

24079/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 419us/step - acc: 0.9913 - loss: 0.0269

24213/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 419us/step - acc: 0.9913 - loss: 0.0269

24337/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 419us/step - acc: 0.9913 - loss: 0.0269

24468/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 419us/step - acc: 0.9913 - loss: 0.0269

24593/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 419us/step - acc: 0.9913 - loss: 0.0269

24725/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 419us/step - acc: 0.9913 - loss: 0.0269

24850/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 418us/step - acc: 0.9913 - loss: 0.0269

24980/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 418us/step - acc: 0.9913 - loss: 0.0269

25111/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 418us/step - acc: 0.9913 - loss: 0.0269

25234/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 418us/step - acc: 0.9913 - loss: 0.0269

25352/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 418us/step - acc: 0.9913 - loss: 0.0269

25466/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 418us/step - acc: 0.9913 - loss: 0.0269

25586/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 418us/step - acc: 0.9913 - loss: 0.0269

25701/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 418us/step - acc: 0.9913 - loss: 0.0269

25814/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 418us/step - acc: 0.9913 - loss: 0.0269

25938/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 418us/step - acc: 0.9913 - loss: 0.0270

26062/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 418us/step - acc: 0.9913 - loss: 0.0270

26189/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 418us/step - acc: 0.9913 - loss: 0.0270

26321/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 418us/step - acc: 0.9913 - loss: 0.0270

26453/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 418us/step - acc: 0.9913 - loss: 0.0270

26585/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 418us/step - acc: 0.9913 - loss: 0.0270

26721/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 417us/step - acc: 0.9913 - loss: 0.0270

26845/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 417us/step - acc: 0.9913 - loss: 0.0270

26945/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 418us/step - acc: 0.9913 - loss: 0.0270

27073/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 418us/step - acc: 0.9913 - loss: 0.0270

27196/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 417us/step - acc: 0.9913 - loss: 0.0270

27325/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 417us/step - acc: 0.9913 - loss: 0.0270

27458/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 417us/step - acc: 0.9913 - loss: 0.0270

27593/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 417us/step - acc: 0.9913 - loss: 0.0270

27726/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 417us/step - acc: 0.9913 - loss: 0.0270

27856/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 417us/step - acc: 0.9913 - loss: 0.0270

27985/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 416us/step - acc: 0.9913 - loss: 0.0270

28098/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 417us/step - acc: 0.9913 - loss: 0.0270

28234/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 416us/step - acc: 0.9913 - loss: 0.0270

28363/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 416us/step - acc: 0.9913 - loss: 0.0270

28499/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 416us/step - acc: 0.9913 - loss: 0.0270

28632/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 416us/step - acc: 0.9913 - loss: 0.0270

28767/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 416us/step - acc: 0.9913 - loss: 0.0270

28906/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 415us/step - acc: 0.9913 - loss: 0.0270

29045/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 415us/step - acc: 0.9913 - loss: 0.0270

29183/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 415us/step - acc: 0.9913 - loss: 0.0270

29318/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 415us/step - acc: 0.9913 - loss: 0.0270

29457/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 414us/step - acc: 0.9913 - loss: 0.0270

29595/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 414us/step - acc: 0.9913 - loss: 0.0270

29732/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 414us/step - acc: 0.9913 - loss: 0.0270

29868/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 414us/step - acc: 0.9913 - loss: 0.0270

29987/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 414us/step - acc: 0.9913 - loss: 0.0270

30112/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 414us/step - acc: 0.9913 - loss: 0.0270

30242/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 414us/step - acc: 0.9913 - loss: 0.0270

30333/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 414us/step - acc: 0.9913 - loss: 0.0270

30435/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 414us/step - acc: 0.9913 - loss: 0.0270

30553/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 414us/step - acc: 0.9913 - loss: 0.0270

30673/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 414us/step - acc: 0.9913 - loss: 0.0270

30800/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 414us/step - acc: 0.9913 - loss: 0.0270

30927/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 414us/step - acc: 0.9913 - loss: 0.0270

31050/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 414us/step - acc: 0.9913 - loss: 0.0270

31180/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 414us/step - acc: 0.9913 - loss: 0.0270

31313/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 414us/step - acc: 0.9913 - loss: 0.0270

31447/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 414us/step - acc: 0.9913 - loss: 0.0270

31578/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 414us/step - acc: 0.9913 - loss: 0.0270

31710/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 413us/step - acc: 0.9913 - loss: 0.0270

31829/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 413us/step - acc: 0.9913 - loss: 0.0270

31952/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 413us/step - acc: 0.9913 - loss: 0.0270

32067/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 414us/step - acc: 0.9913 - loss: 0.0270

32186/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 414us/step - acc: 0.9913 - loss: 0.0270

32308/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 414us/step - acc: 0.9913 - loss: 0.0270

32434/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 414us/step - acc: 0.9913 - loss: 0.0270

32563/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 413us/step - acc: 0.9913 - loss: 0.0271

32693/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 413us/step - acc: 0.9913 - loss: 0.0271

32822/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 413us/step - acc: 0.9913 - loss: 0.0271

32953/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 413us/step - acc: 0.9913 - loss: 0.0271

33067/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 413us/step - acc: 0.9913 - loss: 0.0271

33185/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 413us/step - acc: 0.9913 - loss: 0.0271

33310/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 413us/step - acc: 0.9913 - loss: 0.0271

33434/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 413us/step - acc: 0.9913 - loss: 0.0271

33559/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 413us/step - acc: 0.9913 - loss: 0.0271

33686/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 413us/step - acc: 0.9913 - loss: 0.0271

33812/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 413us/step - acc: 0.9913 - loss: 0.0271

33941/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 413us/step - acc: 0.9913 - loss: 0.0271

34060/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 413us/step - acc: 0.9913 - loss: 0.0271

34177/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 413us/step - acc: 0.9913 - loss: 0.0271

34289/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 413us/step - acc: 0.9913 - loss: 0.0271

34410/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 413us/step - acc: 0.9913 - loss: 0.0271

34533/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 413us/step - acc: 0.9913 - loss: 0.0271

34649/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 413us/step - acc: 0.9913 - loss: 0.0271

34770/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 413us/step - acc: 0.9913 - loss: 0.0271

34895/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 413us/step - acc: 0.9912 - loss: 0.0271

35016/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 413us/step - acc: 0.9912 - loss: 0.0271

35142/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 413us/step - acc: 0.9912 - loss: 0.0271

35271/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 413us/step - acc: 0.9912 - loss: 0.0271

35402/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 413us/step - acc: 0.9912 - loss: 0.0271

35535/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 413us/step - acc: 0.9912 - loss: 0.0271

35669/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 413us/step - acc: 0.9912 - loss: 0.0271

35806/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 412us/step - acc: 0.9912 - loss: 0.0271 

35942/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 412us/step - acc: 0.9912 - loss: 0.0271

36076/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 412us/step - acc: 0.9912 - loss: 0.0271

36208/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 412us/step - acc: 0.9912 - loss: 0.0271

36341/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 412us/step - acc: 0.9912 - loss: 0.0271

36473/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 412us/step - acc: 0.9912 - loss: 0.0271

36599/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 412us/step - acc: 0.9912 - loss: 0.0271

36711/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 412us/step - acc: 0.9912 - loss: 0.0271

36822/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 412us/step - acc: 0.9912 - loss: 0.0271

36944/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 412us/step - acc: 0.9912 - loss: 0.0271

37074/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 412us/step - acc: 0.9912 - loss: 0.0271

37207/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 412us/step - acc: 0.9912 - loss: 0.0271

37340/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 412us/step - acc: 0.9912 - loss: 0.0271

37477/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 411us/step - acc: 0.9912 - loss: 0.0271

37616/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 411us/step - acc: 0.9912 - loss: 0.0271

37754/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 411us/step - acc: 0.9912 - loss: 0.0271

37890/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 411us/step - acc: 0.9912 - loss: 0.0271

38030/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 411us/step - acc: 0.9912 - loss: 0.0272

38167/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 411us/step - acc: 0.9912 - loss: 0.0272

38304/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 410us/step - acc: 0.9912 - loss: 0.0272

38437/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 410us/step - acc: 0.9912 - loss: 0.0272

38573/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 410us/step - acc: 0.9912 - loss: 0.0272

38706/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 410us/step - acc: 0.9912 - loss: 0.0272

38844/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 410us/step - acc: 0.9912 - loss: 0.0272

38982/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 410us/step - acc: 0.9912 - loss: 0.0272

39118/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 410us/step - acc: 0.9912 - loss: 0.0272

39257/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 409us/step - acc: 0.9912 - loss: 0.0272

39394/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 409us/step - acc: 0.9912 - loss: 0.0272

39528/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 409us/step - acc: 0.9912 - loss: 0.0272

39666/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 409us/step - acc: 0.9912 - loss: 0.0272

39804/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 409us/step - acc: 0.9912 - loss: 0.0272

39940/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 409us/step - acc: 0.9912 - loss: 0.0272

40076/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 409us/step - acc: 0.9912 - loss: 0.0272

40207/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 408us/step - acc: 0.9912 - loss: 0.0272

40330/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 408us/step - acc: 0.9912 - loss: 0.0272

40466/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 408us/step - acc: 0.9912 - loss: 0.0272

40602/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 408us/step - acc: 0.9912 - loss: 0.0272

40741/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 408us/step - acc: 0.9912 - loss: 0.0272

40878/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 408us/step - acc: 0.9912 - loss: 0.0272

41015/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 408us/step - acc: 0.9912 - loss: 0.0272

41153/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 408us/step - acc: 0.9912 - loss: 0.0272

41287/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 408us/step - acc: 0.9912 - loss: 0.0272

41421/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 407us/step - acc: 0.9912 - loss: 0.0272

41557/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 407us/step - acc: 0.9912 - loss: 0.0272

41693/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 407us/step - acc: 0.9912 - loss: 0.0272

41831/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 407us/step - acc: 0.9912 - loss: 0.0272

41966/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 407us/step - acc: 0.9912 - loss: 0.0272

42104/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 407us/step - acc: 0.9912 - loss: 0.0272

42241/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 407us/step - acc: 0.9912 - loss: 0.0272

42379/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 406us/step - acc: 0.9912 - loss: 0.0272

42509/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 406us/step - acc: 0.9912 - loss: 0.0273

42642/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 406us/step - acc: 0.9912 - loss: 0.0273

42779/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 406us/step - acc: 0.9912 - loss: 0.0273

42901/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 406us/step - acc: 0.9912 - loss: 0.0273

43039/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 406us/step - acc: 0.9911 - loss: 0.0273

43174/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 406us/step - acc: 0.9911 - loss: 0.0273

43313/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 406us/step - acc: 0.9911 - loss: 0.0273

43449/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 406us/step - acc: 0.9911 - loss: 0.0273

43583/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 406us/step - acc: 0.9911 - loss: 0.0273

43718/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 406us/step - acc: 0.9911 - loss: 0.0273

43855/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.9911 - loss: 0.0273

43993/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.9911 - loss: 0.0273

44131/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.9911 - loss: 0.0273

44270/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.9911 - loss: 0.0273

44405/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.9911 - loss: 0.0273

44530/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.9911 - loss: 0.0273

44655/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.9911 - loss: 0.0273

44783/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.9911 - loss: 0.0273

44908/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.9911 - loss: 0.0273

45034/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.9911 - loss: 0.0273

45165/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 405us/step - acc: 0.9911 - loss: 0.0273

45294/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 405us/step - acc: 0.9911 - loss: 0.0273

45424/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 405us/step - acc: 0.9911 - loss: 0.0273

45560/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 405us/step - acc: 0.9911 - loss: 0.0273

45698/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.9911 - loss: 0.0273

45835/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.9911 - loss: 0.0273

45972/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.9911 - loss: 0.0273

46110/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.9911 - loss: 0.0273

46248/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.9911 - loss: 0.0273

46387/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.9911 - loss: 0.0273

46525/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.9911 - loss: 0.0273

46657/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.9911 - loss: 0.0274

46782/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.9911 - loss: 0.0274

46919/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 404us/step - acc: 0.9911 - loss: 0.0274

47051/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 403us/step - acc: 0.9911 - loss: 0.0274

47182/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 403us/step - acc: 0.9911 - loss: 0.0274

47315/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 403us/step - acc: 0.9911 - loss: 0.0274

47452/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 403us/step - acc: 0.9911 - loss: 0.0274

47588/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 403us/step - acc: 0.9911 - loss: 0.0274

47723/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 403us/step - acc: 0.9911 - loss: 0.0274

47861/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 403us/step - acc: 0.9911 - loss: 0.0274

47999/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 403us/step - acc: 0.9911 - loss: 0.0274

48127/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 403us/step - acc: 0.9911 - loss: 0.0274

48255/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 403us/step - acc: 0.9911 - loss: 0.0274

48386/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 403us/step - acc: 0.9911 - loss: 0.0274

48512/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 403us/step - acc: 0.9911 - loss: 0.0274

48638/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 403us/step - acc: 0.9911 - loss: 0.0274

48768/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 403us/step - acc: 0.9911 - loss: 0.0274

48905/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 403us/step - acc: 0.9911 - loss: 0.0274

49041/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 402us/step - acc: 0.9911 - loss: 0.0274

49177/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 402us/step - acc: 0.9911 - loss: 0.0274

49316/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 402us/step - acc: 0.9911 - loss: 0.0274

49451/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 402us/step - acc: 0.9911 - loss: 0.0274

49584/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 402us/step - acc: 0.9911 - loss: 0.0274

49721/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 402us/step - acc: 0.9911 - loss: 0.0274

49859/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 402us/step - acc: 0.9911 - loss: 0.0274

49997/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 402us/step - acc: 0.9911 - loss: 0.0274

50133/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 402us/step - acc: 0.9911 - loss: 0.0274

50262/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 402us/step - acc: 0.9911 - loss: 0.0274

50381/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 402us/step - acc: 0.9911 - loss: 0.0274

50502/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 402us/step - acc: 0.9911 - loss: 0.0274

50625/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 402us/step - acc: 0.9911 - loss: 0.0274

50744/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 402us/step - acc: 0.9911 - loss: 0.0274

50878/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 402us/step - acc: 0.9911 - loss: 0.0274

51017/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 402us/step - acc: 0.9911 - loss: 0.0274

51152/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 402us/step - acc: 0.9911 - loss: 0.0274

51287/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 401us/step - acc: 0.9911 - loss: 0.0274

51424/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 401us/step - acc: 0.9911 - loss: 0.0274

51561/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 401us/step - acc: 0.9911 - loss: 0.0274

51692/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 401us/step - acc: 0.9911 - loss: 0.0274

51823/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 401us/step - acc: 0.9911 - loss: 0.0274

51959/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 401us/step - acc: 0.9911 - loss: 0.0274

52097/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 401us/step - acc: 0.9911 - loss: 0.0274

52234/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 401us/step - acc: 0.9911 - loss: 0.0274

52373/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 401us/step - acc: 0.9911 - loss: 0.0274

52510/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 401us/step - acc: 0.9911 - loss: 0.0274

52645/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 401us/step - acc: 0.9910 - loss: 0.0274

52782/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 401us/step - acc: 0.9910 - loss: 0.0274

52920/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 400us/step - acc: 0.9910 - loss: 0.0274

53055/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 400us/step - acc: 0.9910 - loss: 0.0274

53192/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 400us/step - acc: 0.9910 - loss: 0.0274

53329/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 400us/step - acc: 0.9910 - loss: 0.0275

53461/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 400us/step - acc: 0.9910 - loss: 0.0275

53597/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 400us/step - acc: 0.9910 - loss: 0.0275

53736/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 400us/step - acc: 0.9910 - loss: 0.0275

53864/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 400us/step - acc: 0.9910 - loss: 0.0275

53997/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 400us/step - acc: 0.9910 - loss: 0.0275

54125/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 400us/step - acc: 0.9910 - loss: 0.0275

54249/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 400us/step - acc: 0.9910 - loss: 0.0275

54373/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 400us/step - acc: 0.9910 - loss: 0.0275

54508/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 400us/step - acc: 0.9910 - loss: 0.0275

54643/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 400us/step - acc: 0.9910 - loss: 0.0275

54781/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 400us/step - acc: 0.9910 - loss: 0.0275

54914/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 400us/step - acc: 0.9910 - loss: 0.0275

55052/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 400us/step - acc: 0.9910 - loss: 0.0275

55188/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 399us/step - acc: 0.9910 - loss: 0.0275

55326/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 399us/step - acc: 0.9910 - loss: 0.0275

55465/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 399us/step - acc: 0.9910 - loss: 0.0275

55602/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 399us/step - acc: 0.9910 - loss: 0.0275

55740/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 399us/step - acc: 0.9910 - loss: 0.0275

55877/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 399us/step - acc: 0.9910 - loss: 0.0275

56013/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 399us/step - acc: 0.9910 - loss: 0.0275

56147/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 399us/step - acc: 0.9910 - loss: 0.0275

56284/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 399us/step - acc: 0.9910 - loss: 0.0275

56422/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 399us/step - acc: 0.9910 - loss: 0.0275

56559/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 399us/step - acc: 0.9910 - loss: 0.0275

56698/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 399us/step - acc: 0.9910 - loss: 0.0275

56838/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 398us/step - acc: 0.9910 - loss: 0.0275

56974/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 398us/step - acc: 0.9910 - loss: 0.0275

57111/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 398us/step - acc: 0.9910 - loss: 0.0275

57248/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 398us/step - acc: 0.9910 - loss: 0.0275

57385/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 398us/step - acc: 0.9910 - loss: 0.0275

57521/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 398us/step - acc: 0.9910 - loss: 0.0275

57658/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 398us/step - acc: 0.9910 - loss: 0.0276

57795/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 398us/step - acc: 0.9910 - loss: 0.0276

57932/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 398us/step - acc: 0.9910 - loss: 0.0276

58071/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 398us/step - acc: 0.9910 - loss: 0.0276

58209/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 398us/step - acc: 0.9910 - loss: 0.0276

58348/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 398us/step - acc: 0.9910 - loss: 0.0276

58487/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 398us/step - acc: 0.9910 - loss: 0.0276

58625/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9910 - loss: 0.0276

58762/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9910 - loss: 0.0276

58899/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9910 - loss: 0.0276

59035/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9910 - loss: 0.0276

59173/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9910 - loss: 0.0276

59309/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9910 - loss: 0.0276

59447/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9910 - loss: 0.0276

59519/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 397us/step - acc: 0.9910 - loss: 0.0276

59617/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 398us/step - acc: 0.9910 - loss: 0.0276

59738/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 398us/step - acc: 0.9910 - loss: 0.0276

59865/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 398us/step - acc: 0.9910 - loss: 0.0276

59981/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 398us/step - acc: 0.9910 - loss: 0.0276

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 461us/step - acc: 0.9910 - loss: 0.0276 - val_acc: 0.9723 - val_loss: 0.1081

Epoch 17/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 15:10 15ms/step - acc: 1.0000 - loss: 0.0019

  119/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 425us/step - acc: 0.9796 - loss: 0.0919 

  240/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 420us/step - acc: 0.9870 - loss: 0.0648

  360/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 419us/step - acc: 0.9894 - loss: 0.0539

  481/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 418us/step - acc: 0.9899 - loss: 0.0490

  602/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 418us/step - acc: 0.9900 - loss: 0.0466

  701/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 430us/step - acc: 0.9901 - loss: 0.0451

  795/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 443us/step - acc: 0.9901 - loss: 0.0438

  852/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 473us/step - acc: 0.9902 - loss: 0.0429

  907/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 500us/step - acc: 0.9903 - loss: 0.0422

  960/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 525us/step - acc: 0.9903 - loss: 0.0417

 1040/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 533us/step - acc: 0.9903 - loss: 0.0409

 1118/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 541us/step - acc: 0.9903 - loss: 0.0404

 1194/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 548us/step - acc: 0.9903 - loss: 0.0400

 1251/60000 ━━━━━━━━━━━━━━━━━━━━ 33s 564us/step - acc: 0.9902 - loss: 0.0397

 1343/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 562us/step - acc: 0.9902 - loss: 0.0392

 1425/60000 ━━━━━━━━━━━━━━━━━━━━ 33s 565us/step - acc: 0.9902 - loss: 0.0388

 1523/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 562us/step - acc: 0.9903 - loss: 0.0382

 1630/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 556us/step - acc: 0.9903 - loss: 0.0377

 1735/60000 ━━━━━━━━━━━━━━━━━━━━ 32s 551us/step - acc: 0.9904 - loss: 0.0372

 1840/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 547us/step - acc: 0.9904 - loss: 0.0368

 1934/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 547us/step - acc: 0.9905 - loss: 0.0364

 2040/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 543us/step - acc: 0.9905 - loss: 0.0359

 2153/60000 ━━━━━━━━━━━━━━━━━━━━ 31s 538us/step - acc: 0.9906 - loss: 0.0354

 2264/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 533us/step - acc: 0.9906 - loss: 0.0349

 2382/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 528us/step - acc: 0.9907 - loss: 0.0345

 2500/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 523us/step - acc: 0.9907 - loss: 0.0340

 2623/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 518us/step - acc: 0.9908 - loss: 0.0336

 2744/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 513us/step - acc: 0.9908 - loss: 0.0332

 2864/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 509us/step - acc: 0.9909 - loss: 0.0328

 2982/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 506us/step - acc: 0.9909 - loss: 0.0324

 3104/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 502us/step - acc: 0.9909 - loss: 0.0321

 3226/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 499us/step - acc: 0.9910 - loss: 0.0317

 3336/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 497us/step - acc: 0.9910 - loss: 0.0314

 3450/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 495us/step - acc: 0.9910 - loss: 0.0311

 3567/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 493us/step - acc: 0.9911 - loss: 0.0308

 3676/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 492us/step - acc: 0.9911 - loss: 0.0305

 3796/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 490us/step - acc: 0.9912 - loss: 0.0302

 3916/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 488us/step - acc: 0.9912 - loss: 0.0299

 4032/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 486us/step - acc: 0.9913 - loss: 0.0296

 4153/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 484us/step - acc: 0.9913 - loss: 0.0294

 4259/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 484us/step - acc: 0.9914 - loss: 0.0292

 4357/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 484us/step - acc: 0.9914 - loss: 0.0290

 4466/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 484us/step - acc: 0.9914 - loss: 0.0288

 4558/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 485us/step - acc: 0.9915 - loss: 0.0287

 4665/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 485us/step - acc: 0.9915 - loss: 0.0285

 4768/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 485us/step - acc: 0.9915 - loss: 0.0283

 4881/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 484us/step - acc: 0.9915 - loss: 0.0282

 4983/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 484us/step - acc: 0.9916 - loss: 0.0281

 5099/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 483us/step - acc: 0.9916 - loss: 0.0280

 5202/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 483us/step - acc: 0.9916 - loss: 0.0279

 5319/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 482us/step - acc: 0.9916 - loss: 0.0278

 5436/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 481us/step - acc: 0.9916 - loss: 0.0277

 5554/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 480us/step - acc: 0.9916 - loss: 0.0276

 5667/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 479us/step - acc: 0.9916 - loss: 0.0276

 5724/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 483us/step - acc: 0.9916 - loss: 0.0275

 5808/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 485us/step - acc: 0.9916 - loss: 0.0275

 5892/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 486us/step - acc: 0.9915 - loss: 0.0274

 5980/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 488us/step - acc: 0.9915 - loss: 0.0274

 6048/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 491us/step - acc: 0.9915 - loss: 0.0274

 6138/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 492us/step - acc: 0.9915 - loss: 0.0273

 6240/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 492us/step - acc: 0.9915 - loss: 0.0273

 6339/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 492us/step - acc: 0.9915 - loss: 0.0272

 6434/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 492us/step - acc: 0.9915 - loss: 0.0272

 6523/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 493us/step - acc: 0.9915 - loss: 0.0271

 6634/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 493us/step - acc: 0.9915 - loss: 0.0271

 6751/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 492us/step - acc: 0.9915 - loss: 0.0271

 6852/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 492us/step - acc: 0.9915 - loss: 0.0270

 6938/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 493us/step - acc: 0.9914 - loss: 0.0270

 6991/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 497us/step - acc: 0.9914 - loss: 0.0270

 7001/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 504us/step - acc: 0.9914 - loss: 0.0270

 7052/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 507us/step - acc: 0.9914 - loss: 0.0270

 7112/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 510us/step - acc: 0.9914 - loss: 0.0269

 7199/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 511us/step - acc: 0.9914 - loss: 0.0269

 7287/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 512us/step - acc: 0.9914 - loss: 0.0269

 7388/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 512us/step - acc: 0.9914 - loss: 0.0269

 7496/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 511us/step - acc: 0.9914 - loss: 0.0268

 7602/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 510us/step - acc: 0.9914 - loss: 0.0268

 7706/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 510us/step - acc: 0.9913 - loss: 0.0268

 7801/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 510us/step - acc: 0.9913 - loss: 0.0268

 7886/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 511us/step - acc: 0.9913 - loss: 0.0268

 7991/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 511us/step - acc: 0.9913 - loss: 0.0268

 8060/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 513us/step - acc: 0.9913 - loss: 0.0267

 8154/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 513us/step - acc: 0.9913 - loss: 0.0267

 8256/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 513us/step - acc: 0.9913 - loss: 0.0267

 8378/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 511us/step - acc: 0.9913 - loss: 0.0267

 8492/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 510us/step - acc: 0.9913 - loss: 0.0267

 8604/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 509us/step - acc: 0.9913 - loss: 0.0267

 8709/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 509us/step - acc: 0.9912 - loss: 0.0267

 8811/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 509us/step - acc: 0.9912 - loss: 0.0267

 8894/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 510us/step - acc: 0.9912 - loss: 0.0266

 8977/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 511us/step - acc: 0.9912 - loss: 0.0266

 9072/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 511us/step - acc: 0.9912 - loss: 0.0266

 9157/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 512us/step - acc: 0.9912 - loss: 0.0266

 9264/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 511us/step - acc: 0.9912 - loss: 0.0266

 9368/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 511us/step - acc: 0.9912 - loss: 0.0266

 9464/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 511us/step - acc: 0.9912 - loss: 0.0265

 9575/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 510us/step - acc: 0.9912 - loss: 0.0265

 9690/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 509us/step - acc: 0.9912 - loss: 0.0265

 9774/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 510us/step - acc: 0.9912 - loss: 0.0265

 9878/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 510us/step - acc: 0.9912 - loss: 0.0265

10001/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 509us/step - acc: 0.9912 - loss: 0.0265

10119/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 508us/step - acc: 0.9912 - loss: 0.0264

10226/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 507us/step - acc: 0.9912 - loss: 0.0264

10323/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 507us/step - acc: 0.9912 - loss: 0.0264

10431/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 507us/step - acc: 0.9912 - loss: 0.0264

10535/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 507us/step - acc: 0.9912 - loss: 0.0264

10649/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 506us/step - acc: 0.9912 - loss: 0.0263

10762/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 505us/step - acc: 0.9912 - loss: 0.0263

10876/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 505us/step - acc: 0.9912 - loss: 0.0263

10993/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 504us/step - acc: 0.9912 - loss: 0.0263

11113/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 503us/step - acc: 0.9912 - loss: 0.0263

11233/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 502us/step - acc: 0.9912 - loss: 0.0263

11356/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 501us/step - acc: 0.9911 - loss: 0.0263

11484/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 500us/step - acc: 0.9911 - loss: 0.0263

11605/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 499us/step - acc: 0.9911 - loss: 0.0263

11722/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 498us/step - acc: 0.9911 - loss: 0.0263

11839/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 498us/step - acc: 0.9911 - loss: 0.0263

11956/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 497us/step - acc: 0.9911 - loss: 0.0263

12062/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 497us/step - acc: 0.9911 - loss: 0.0263

12141/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 498us/step - acc: 0.9911 - loss: 0.0263

12257/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 497us/step - acc: 0.9911 - loss: 0.0263

12380/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 496us/step - acc: 0.9911 - loss: 0.0263

12498/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 495us/step - acc: 0.9911 - loss: 0.0263

12580/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 496us/step - acc: 0.9911 - loss: 0.0263

12679/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 496us/step - acc: 0.9911 - loss: 0.0263

12797/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 496us/step - acc: 0.9911 - loss: 0.0263

12914/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 495us/step - acc: 0.9911 - loss: 0.0263

13031/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 494us/step - acc: 0.9911 - loss: 0.0262

13154/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 494us/step - acc: 0.9911 - loss: 0.0262

13256/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 494us/step - acc: 0.9911 - loss: 0.0262

13357/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 494us/step - acc: 0.9911 - loss: 0.0262

13466/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 493us/step - acc: 0.9911 - loss: 0.0262

13584/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 493us/step - acc: 0.9911 - loss: 0.0262

13708/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 492us/step - acc: 0.9911 - loss: 0.0262

13820/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 492us/step - acc: 0.9910 - loss: 0.0262

13914/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 492us/step - acc: 0.9910 - loss: 0.0262

14028/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 491us/step - acc: 0.9910 - loss: 0.0262

14148/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 491us/step - acc: 0.9910 - loss: 0.0262

14266/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 490us/step - acc: 0.9910 - loss: 0.0262

14390/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 490us/step - acc: 0.9910 - loss: 0.0262

14512/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 489us/step - acc: 0.9910 - loss: 0.0262

14629/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 488us/step - acc: 0.9910 - loss: 0.0262

14744/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 488us/step - acc: 0.9910 - loss: 0.0262

14860/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 488us/step - acc: 0.9910 - loss: 0.0262

14982/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 487us/step - acc: 0.9910 - loss: 0.0262

15103/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 486us/step - acc: 0.9910 - loss: 0.0262

15225/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 486us/step - acc: 0.9910 - loss: 0.0262

15346/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 485us/step - acc: 0.9910 - loss: 0.0262

15465/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 485us/step - acc: 0.9910 - loss: 0.0262

15587/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 484us/step - acc: 0.9910 - loss: 0.0262

15713/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 483us/step - acc: 0.9910 - loss: 0.0262

15835/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 483us/step - acc: 0.9910 - loss: 0.0262

15971/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 482us/step - acc: 0.9910 - loss: 0.0262

16103/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 481us/step - acc: 0.9910 - loss: 0.0262

16239/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 480us/step - acc: 0.9910 - loss: 0.0262

16373/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 479us/step - acc: 0.9910 - loss: 0.0262

16507/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 478us/step - acc: 0.9910 - loss: 0.0262

16642/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 478us/step - acc: 0.9910 - loss: 0.0262

16770/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 477us/step - acc: 0.9910 - loss: 0.0262

16895/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 476us/step - acc: 0.9909 - loss: 0.0262

17020/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 476us/step - acc: 0.9909 - loss: 0.0262

17151/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 475us/step - acc: 0.9909 - loss: 0.0262

17284/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 474us/step - acc: 0.9909 - loss: 0.0262

17418/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 474us/step - acc: 0.9909 - loss: 0.0262

17554/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 473us/step - acc: 0.9909 - loss: 0.0262

17687/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 472us/step - acc: 0.9909 - loss: 0.0262

17822/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 471us/step - acc: 0.9909 - loss: 0.0262

17956/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 471us/step - acc: 0.9909 - loss: 0.0262

18092/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 470us/step - acc: 0.9909 - loss: 0.0262

18229/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 469us/step - acc: 0.9909 - loss: 0.0262

18361/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 468us/step - acc: 0.9909 - loss: 0.0262

18498/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 468us/step - acc: 0.9909 - loss: 0.0262

18635/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 467us/step - acc: 0.9909 - loss: 0.0262

18774/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 466us/step - acc: 0.9909 - loss: 0.0262

18900/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 466us/step - acc: 0.9909 - loss: 0.0262

19027/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 465us/step - acc: 0.9909 - loss: 0.0262

19164/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 464us/step - acc: 0.9909 - loss: 0.0262

19299/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 464us/step - acc: 0.9909 - loss: 0.0262

19436/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 463us/step - acc: 0.9909 - loss: 0.0262

19573/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 462us/step - acc: 0.9909 - loss: 0.0262

19711/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 462us/step - acc: 0.9909 - loss: 0.0262

19844/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 461us/step - acc: 0.9909 - loss: 0.0262

19980/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 461us/step - acc: 0.9908 - loss: 0.0262

20091/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 461us/step - acc: 0.9908 - loss: 0.0262

20204/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 460us/step - acc: 0.9908 - loss: 0.0262

20314/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 460us/step - acc: 0.9908 - loss: 0.0262

20447/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 460us/step - acc: 0.9908 - loss: 0.0262

20582/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 459us/step - acc: 0.9908 - loss: 0.0262

20711/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 459us/step - acc: 0.9908 - loss: 0.0262

20850/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 458us/step - acc: 0.9908 - loss: 0.0262

20985/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 458us/step - acc: 0.9908 - loss: 0.0262

21124/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 457us/step - acc: 0.9908 - loss: 0.0262

21262/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 456us/step - acc: 0.9908 - loss: 0.0262

21400/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 456us/step - acc: 0.9908 - loss: 0.0262

21538/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 455us/step - acc: 0.9908 - loss: 0.0263

21677/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 455us/step - acc: 0.9908 - loss: 0.0263

21817/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 454us/step - acc: 0.9908 - loss: 0.0263

21954/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 453us/step - acc: 0.9908 - loss: 0.0263

22087/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 453us/step - acc: 0.9908 - loss: 0.0263

22221/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 452us/step - acc: 0.9908 - loss: 0.0263

22359/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 452us/step - acc: 0.9908 - loss: 0.0263

22496/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 451us/step - acc: 0.9908 - loss: 0.0263

22630/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 451us/step - acc: 0.9908 - loss: 0.0263

22765/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 450us/step - acc: 0.9908 - loss: 0.0263

22901/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 450us/step - acc: 0.9908 - loss: 0.0263

23040/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 449us/step - acc: 0.9908 - loss: 0.0263

23176/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 449us/step - acc: 0.9908 - loss: 0.0263

23313/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 448us/step - acc: 0.9908 - loss: 0.0263

23454/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 448us/step - acc: 0.9907 - loss: 0.0263

23593/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 447us/step - acc: 0.9907 - loss: 0.0263

23734/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 447us/step - acc: 0.9907 - loss: 0.0263

23874/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 446us/step - acc: 0.9907 - loss: 0.0263

24009/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 446us/step - acc: 0.9907 - loss: 0.0263

24148/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 445us/step - acc: 0.9907 - loss: 0.0263

24287/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 445us/step - acc: 0.9907 - loss: 0.0264

24426/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 445us/step - acc: 0.9907 - loss: 0.0264

24565/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 444us/step - acc: 0.9907 - loss: 0.0264

24702/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 444us/step - acc: 0.9907 - loss: 0.0264

24836/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 443us/step - acc: 0.9907 - loss: 0.0264

24973/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 443us/step - acc: 0.9907 - loss: 0.0264

25111/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 442us/step - acc: 0.9907 - loss: 0.0264

25249/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 442us/step - acc: 0.9907 - loss: 0.0264

25383/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 442us/step - acc: 0.9907 - loss: 0.0264

25521/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 441us/step - acc: 0.9907 - loss: 0.0264

25656/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 441us/step - acc: 0.9907 - loss: 0.0264

25796/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 440us/step - acc: 0.9907 - loss: 0.0264

25932/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 440us/step - acc: 0.9907 - loss: 0.0264

26067/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 440us/step - acc: 0.9907 - loss: 0.0264

26198/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 439us/step - acc: 0.9907 - loss: 0.0264

26317/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 439us/step - acc: 0.9907 - loss: 0.0264

26439/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 439us/step - acc: 0.9907 - loss: 0.0264

26561/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 439us/step - acc: 0.9907 - loss: 0.0264

26677/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 439us/step - acc: 0.9907 - loss: 0.0264

26798/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 439us/step - acc: 0.9907 - loss: 0.0264

26917/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 439us/step - acc: 0.9907 - loss: 0.0264

27039/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 439us/step - acc: 0.9907 - loss: 0.0264

27162/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 439us/step - acc: 0.9907 - loss: 0.0264

27288/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 438us/step - acc: 0.9907 - loss: 0.0264

27411/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 438us/step - acc: 0.9907 - loss: 0.0264

27537/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 438us/step - acc: 0.9907 - loss: 0.0264

27661/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 438us/step - acc: 0.9907 - loss: 0.0264

27777/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 438us/step - acc: 0.9907 - loss: 0.0264

27896/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 438us/step - acc: 0.9907 - loss: 0.0264

28016/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 438us/step - acc: 0.9907 - loss: 0.0264

28141/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 438us/step - acc: 0.9907 - loss: 0.0264

28265/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 437us/step - acc: 0.9907 - loss: 0.0264

28387/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 437us/step - acc: 0.9907 - loss: 0.0264

28512/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 437us/step - acc: 0.9907 - loss: 0.0264

28634/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 437us/step - acc: 0.9907 - loss: 0.0264

28760/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 437us/step - acc: 0.9907 - loss: 0.0264

28884/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 437us/step - acc: 0.9907 - loss: 0.0264

29004/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 437us/step - acc: 0.9907 - loss: 0.0264

29114/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 437us/step - acc: 0.9907 - loss: 0.0264

29236/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 437us/step - acc: 0.9907 - loss: 0.0264

29360/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 437us/step - acc: 0.9907 - loss: 0.0264

29462/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 437us/step - acc: 0.9907 - loss: 0.0264

29582/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 437us/step - acc: 0.9907 - loss: 0.0264

29700/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 437us/step - acc: 0.9907 - loss: 0.0264

29816/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 437us/step - acc: 0.9907 - loss: 0.0263

29941/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 436us/step - acc: 0.9907 - loss: 0.0263

30063/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 436us/step - acc: 0.9907 - loss: 0.0263

30183/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 436us/step - acc: 0.9907 - loss: 0.0263

30299/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 436us/step - acc: 0.9907 - loss: 0.0263

30417/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 436us/step - acc: 0.9907 - loss: 0.0263

30534/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 436us/step - acc: 0.9907 - loss: 0.0263

30649/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 436us/step - acc: 0.9907 - loss: 0.0263

30756/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 436us/step - acc: 0.9907 - loss: 0.0263

30867/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 436us/step - acc: 0.9907 - loss: 0.0263

30982/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 436us/step - acc: 0.9907 - loss: 0.0263

31097/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 436us/step - acc: 0.9907 - loss: 0.0263

31217/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 436us/step - acc: 0.9907 - loss: 0.0263

31341/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 436us/step - acc: 0.9907 - loss: 0.0263

31450/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 436us/step - acc: 0.9907 - loss: 0.0263

31570/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 436us/step - acc: 0.9907 - loss: 0.0263

31695/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 436us/step - acc: 0.9907 - loss: 0.0263

31824/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 436us/step - acc: 0.9907 - loss: 0.0263

31943/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 436us/step - acc: 0.9907 - loss: 0.0263

32056/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 436us/step - acc: 0.9907 - loss: 0.0263

32184/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 436us/step - acc: 0.9907 - loss: 0.0263

32315/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 435us/step - acc: 0.9907 - loss: 0.0263

32442/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 435us/step - acc: 0.9907 - loss: 0.0263

32539/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 435us/step - acc: 0.9907 - loss: 0.0263

32658/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 435us/step - acc: 0.9907 - loss: 0.0263

32771/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 435us/step - acc: 0.9907 - loss: 0.0263

32891/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 435us/step - acc: 0.9907 - loss: 0.0263

33006/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 435us/step - acc: 0.9907 - loss: 0.0263

33123/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 435us/step - acc: 0.9907 - loss: 0.0263

33246/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 435us/step - acc: 0.9907 - loss: 0.0263

33371/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 435us/step - acc: 0.9907 - loss: 0.0263

33491/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 435us/step - acc: 0.9907 - loss: 0.0263

33618/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 435us/step - acc: 0.9907 - loss: 0.0263

33741/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 435us/step - acc: 0.9907 - loss: 0.0263

33865/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 435us/step - acc: 0.9907 - loss: 0.0263

33985/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 435us/step - acc: 0.9907 - loss: 0.0263

34101/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 435us/step - acc: 0.9907 - loss: 0.0263

34201/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 435us/step - acc: 0.9907 - loss: 0.0263

34317/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 435us/step - acc: 0.9907 - loss: 0.0263

34446/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 435us/step - acc: 0.9907 - loss: 0.0263

34571/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 435us/step - acc: 0.9907 - loss: 0.0262

34700/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9907 - loss: 0.0262

34812/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9907 - loss: 0.0262

34934/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9907 - loss: 0.0262

35049/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9907 - loss: 0.0262

35171/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 434us/step - acc: 0.9907 - loss: 0.0262

35249/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 435us/step - acc: 0.9907 - loss: 0.0262

35307/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 436us/step - acc: 0.9907 - loss: 0.0262

35354/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 436us/step - acc: 0.9907 - loss: 0.0262

35444/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 437us/step - acc: 0.9907 - loss: 0.0262

35555/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 437us/step - acc: 0.9907 - loss: 0.0263

35670/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 437us/step - acc: 0.9907 - loss: 0.0263

35789/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 437us/step - acc: 0.9907 - loss: 0.0263

35913/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 437us/step - acc: 0.9907 - loss: 0.0263

36034/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 436us/step - acc: 0.9907 - loss: 0.0263

36160/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 436us/step - acc: 0.9907 - loss: 0.0263

36294/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 436us/step - acc: 0.9907 - loss: 0.0263

36419/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 436us/step - acc: 0.9907 - loss: 0.0263

36542/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 436us/step - acc: 0.9907 - loss: 0.0263

36655/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 436us/step - acc: 0.9907 - loss: 0.0263

36777/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 436us/step - acc: 0.9907 - loss: 0.0262

36905/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 436us/step - acc: 0.9907 - loss: 0.0262

37037/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 435us/step - acc: 0.9907 - loss: 0.0262

37172/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 435us/step - acc: 0.9907 - loss: 0.0262 

37307/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 435us/step - acc: 0.9907 - loss: 0.0262

37444/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 435us/step - acc: 0.9907 - loss: 0.0262

37580/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 435us/step - acc: 0.9907 - loss: 0.0262

37714/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 434us/step - acc: 0.9907 - loss: 0.0262

37853/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 434us/step - acc: 0.9907 - loss: 0.0262

37985/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 434us/step - acc: 0.9907 - loss: 0.0262

38119/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 434us/step - acc: 0.9907 - loss: 0.0262

38256/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 433us/step - acc: 0.9907 - loss: 0.0262

38381/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 433us/step - acc: 0.9907 - loss: 0.0262

38510/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 433us/step - acc: 0.9907 - loss: 0.0262

38640/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 433us/step - acc: 0.9907 - loss: 0.0262

38772/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 433us/step - acc: 0.9907 - loss: 0.0262

38901/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 433us/step - acc: 0.9907 - loss: 0.0262

39030/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 433us/step - acc: 0.9907 - loss: 0.0262

39161/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 432us/step - acc: 0.9907 - loss: 0.0262

39286/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 432us/step - acc: 0.9907 - loss: 0.0262

39423/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 432us/step - acc: 0.9907 - loss: 0.0262

39562/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 432us/step - acc: 0.9907 - loss: 0.0262

39698/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 432us/step - acc: 0.9907 - loss: 0.0262

39836/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 431us/step - acc: 0.9907 - loss: 0.0262

39972/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 431us/step - acc: 0.9907 - loss: 0.0262

40107/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 431us/step - acc: 0.9907 - loss: 0.0262

40246/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 431us/step - acc: 0.9907 - loss: 0.0262

40382/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 430us/step - acc: 0.9907 - loss: 0.0262

40519/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 430us/step - acc: 0.9907 - loss: 0.0262

40656/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 430us/step - acc: 0.9907 - loss: 0.0262

40793/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 430us/step - acc: 0.9907 - loss: 0.0262

40930/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 430us/step - acc: 0.9907 - loss: 0.0262

41059/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 429us/step - acc: 0.9907 - loss: 0.0262

41189/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 429us/step - acc: 0.9907 - loss: 0.0262

41314/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 429us/step - acc: 0.9907 - loss: 0.0262

41451/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 429us/step - acc: 0.9907 - loss: 0.0262

41590/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 429us/step - acc: 0.9907 - loss: 0.0262

41727/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 429us/step - acc: 0.9907 - loss: 0.0262

41864/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 428us/step - acc: 0.9907 - loss: 0.0262

41988/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 428us/step - acc: 0.9907 - loss: 0.0262

42123/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 428us/step - acc: 0.9907 - loss: 0.0262

42260/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 428us/step - acc: 0.9907 - loss: 0.0262

42400/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 428us/step - acc: 0.9907 - loss: 0.0262

42538/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 428us/step - acc: 0.9907 - loss: 0.0262

42676/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 427us/step - acc: 0.9907 - loss: 0.0262

42814/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 427us/step - acc: 0.9907 - loss: 0.0262

42953/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 427us/step - acc: 0.9907 - loss: 0.0262

43089/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 427us/step - acc: 0.9907 - loss: 0.0262

43215/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 427us/step - acc: 0.9907 - loss: 0.0262

43337/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 427us/step - acc: 0.9907 - loss: 0.0262

43464/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 427us/step - acc: 0.9907 - loss: 0.0262

43593/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 426us/step - acc: 0.9907 - loss: 0.0262

43720/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 426us/step - acc: 0.9907 - loss: 0.0262

43842/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 426us/step - acc: 0.9907 - loss: 0.0262

43965/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 426us/step - acc: 0.9907 - loss: 0.0262

44095/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 426us/step - acc: 0.9907 - loss: 0.0262

44231/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 426us/step - acc: 0.9907 - loss: 0.0262

44367/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 426us/step - acc: 0.9907 - loss: 0.0262

44502/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 426us/step - acc: 0.9907 - loss: 0.0262

44629/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 425us/step - acc: 0.9907 - loss: 0.0262

44757/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 425us/step - acc: 0.9907 - loss: 0.0262

44894/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 425us/step - acc: 0.9907 - loss: 0.0262

45030/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 425us/step - acc: 0.9907 - loss: 0.0262

45163/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 425us/step - acc: 0.9907 - loss: 0.0263

45296/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 425us/step - acc: 0.9907 - loss: 0.0263

45429/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 425us/step - acc: 0.9907 - loss: 0.0263

45566/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 424us/step - acc: 0.9907 - loss: 0.0263

45700/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 424us/step - acc: 0.9907 - loss: 0.0263

45833/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 424us/step - acc: 0.9907 - loss: 0.0263

45966/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 424us/step - acc: 0.9907 - loss: 0.0263

46087/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 424us/step - acc: 0.9907 - loss: 0.0263

46220/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 424us/step - acc: 0.9907 - loss: 0.0263

46355/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 424us/step - acc: 0.9907 - loss: 0.0263

46492/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 424us/step - acc: 0.9907 - loss: 0.0263

46629/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 423us/step - acc: 0.9907 - loss: 0.0263

46767/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 423us/step - acc: 0.9907 - loss: 0.0263

46906/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 423us/step - acc: 0.9907 - loss: 0.0263

47043/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 423us/step - acc: 0.9907 - loss: 0.0263

47177/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 423us/step - acc: 0.9907 - loss: 0.0263

47307/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 423us/step - acc: 0.9907 - loss: 0.0263

47442/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 423us/step - acc: 0.9907 - loss: 0.0263

47579/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 422us/step - acc: 0.9907 - loss: 0.0263

47715/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 422us/step - acc: 0.9907 - loss: 0.0263

47852/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 422us/step - acc: 0.9907 - loss: 0.0263

47987/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 422us/step - acc: 0.9907 - loss: 0.0263

48123/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 422us/step - acc: 0.9907 - loss: 0.0263

48259/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 422us/step - acc: 0.9907 - loss: 0.0263

48397/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 421us/step - acc: 0.9907 - loss: 0.0263

48534/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 421us/step - acc: 0.9907 - loss: 0.0263

48669/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 421us/step - acc: 0.9907 - loss: 0.0263

48805/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 421us/step - acc: 0.9907 - loss: 0.0263

48944/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 421us/step - acc: 0.9907 - loss: 0.0263

49082/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 421us/step - acc: 0.9907 - loss: 0.0263

49219/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 421us/step - acc: 0.9907 - loss: 0.0263

49356/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 420us/step - acc: 0.9907 - loss: 0.0263

49494/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 420us/step - acc: 0.9907 - loss: 0.0263

49628/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 420us/step - acc: 0.9907 - loss: 0.0263

49761/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 420us/step - acc: 0.9907 - loss: 0.0263

49898/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 420us/step - acc: 0.9907 - loss: 0.0263

50036/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 420us/step - acc: 0.9907 - loss: 0.0263

50153/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 420us/step - acc: 0.9907 - loss: 0.0263

50288/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 420us/step - acc: 0.9907 - loss: 0.0263

50423/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 419us/step - acc: 0.9907 - loss: 0.0263

50558/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9907 - loss: 0.0263

50691/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9907 - loss: 0.0263

50827/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9907 - loss: 0.0263

50964/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9907 - loss: 0.0264

51101/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9907 - loss: 0.0264

51236/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9907 - loss: 0.0264

51372/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 419us/step - acc: 0.9907 - loss: 0.0264

51509/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 418us/step - acc: 0.9907 - loss: 0.0264

51644/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 418us/step - acc: 0.9907 - loss: 0.0264

51778/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 418us/step - acc: 0.9907 - loss: 0.0264

51913/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 418us/step - acc: 0.9907 - loss: 0.0264

52050/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 418us/step - acc: 0.9907 - loss: 0.0264

52186/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 418us/step - acc: 0.9907 - loss: 0.0264

52322/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 418us/step - acc: 0.9907 - loss: 0.0264

52458/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 417us/step - acc: 0.9907 - loss: 0.0264

52593/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 417us/step - acc: 0.9907 - loss: 0.0264

52725/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 417us/step - acc: 0.9907 - loss: 0.0264

52861/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 417us/step - acc: 0.9907 - loss: 0.0264

53000/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 417us/step - acc: 0.9907 - loss: 0.0264

53139/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 417us/step - acc: 0.9907 - loss: 0.0264

53273/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 417us/step - acc: 0.9907 - loss: 0.0264

53407/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 417us/step - acc: 0.9907 - loss: 0.0264

53545/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 417us/step - acc: 0.9907 - loss: 0.0264

53682/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 416us/step - acc: 0.9907 - loss: 0.0264

53818/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 416us/step - acc: 0.9907 - loss: 0.0264

53953/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 416us/step - acc: 0.9907 - loss: 0.0264

54088/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 416us/step - acc: 0.9907 - loss: 0.0264

54224/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 416us/step - acc: 0.9907 - loss: 0.0264

54361/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 416us/step - acc: 0.9907 - loss: 0.0264

54498/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 416us/step - acc: 0.9907 - loss: 0.0264

54632/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 416us/step - acc: 0.9907 - loss: 0.0265

54768/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9907 - loss: 0.0265

54906/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9907 - loss: 0.0265

55041/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9907 - loss: 0.0265

55177/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9907 - loss: 0.0265

55313/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 415us/step - acc: 0.9907 - loss: 0.0265

55448/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 415us/step - acc: 0.9907 - loss: 0.0265

55586/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 415us/step - acc: 0.9907 - loss: 0.0265

55724/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 415us/step - acc: 0.9907 - loss: 0.0265

55863/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 414us/step - acc: 0.9907 - loss: 0.0265

56001/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 414us/step - acc: 0.9907 - loss: 0.0265

56137/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 414us/step - acc: 0.9907 - loss: 0.0265

56273/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 414us/step - acc: 0.9907 - loss: 0.0265

56410/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 414us/step - acc: 0.9907 - loss: 0.0265

56549/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 414us/step - acc: 0.9907 - loss: 0.0265

56686/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 414us/step - acc: 0.9907 - loss: 0.0265

56824/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 414us/step - acc: 0.9907 - loss: 0.0265

56964/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 414us/step - acc: 0.9907 - loss: 0.0265

57099/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 413us/step - acc: 0.9907 - loss: 0.0265

57237/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 413us/step - acc: 0.9907 - loss: 0.0265

57375/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 413us/step - acc: 0.9907 - loss: 0.0265

57514/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 413us/step - acc: 0.9907 - loss: 0.0265

57650/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 413us/step - acc: 0.9907 - loss: 0.0265

57786/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 413us/step - acc: 0.9907 - loss: 0.0266

57923/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 413us/step - acc: 0.9907 - loss: 0.0266

58059/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 413us/step - acc: 0.9907 - loss: 0.0266

58198/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 413us/step - acc: 0.9907 - loss: 0.0266

58335/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 412us/step - acc: 0.9907 - loss: 0.0266

58476/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 412us/step - acc: 0.9907 - loss: 0.0266

58614/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 412us/step - acc: 0.9907 - loss: 0.0266

58741/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 412us/step - acc: 0.9907 - loss: 0.0266

58876/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 412us/step - acc: 0.9907 - loss: 0.0266

59015/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 412us/step - acc: 0.9907 - loss: 0.0266

59152/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 412us/step - acc: 0.9907 - loss: 0.0266

59290/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 412us/step - acc: 0.9907 - loss: 0.0266

59428/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 412us/step - acc: 0.9907 - loss: 0.0266

59566/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 411us/step - acc: 0.9907 - loss: 0.0266

59708/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 411us/step - acc: 0.9907 - loss: 0.0266

59847/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 411us/step - acc: 0.9907 - loss: 0.0266

59982/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 411us/step - acc: 0.9907 - loss: 0.0266

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 471us/step - acc: 0.9907 - loss: 0.0266 - val_acc: 0.9705 - val_loss: 0.1160

Epoch 18/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 9:41 10ms/step - acc: 1.0000 - loss: 8.2609e-05

  136/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 371us/step - acc: 0.9925 - loss: 0.0176    

  270/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 374us/step - acc: 0.9902 - loss: 0.0218

  402/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 376us/step - acc: 0.9880 - loss: 0.0252

  534/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 377us/step - acc: 0.9875 - loss: 0.0261

  661/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 380us/step - acc: 0.9871 - loss: 0.0276

  794/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 379us/step - acc: 0.9871 - loss: 0.0286

  925/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 380us/step - acc: 0.9872 - loss: 0.0298

 1059/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 379us/step - acc: 0.9871 - loss: 0.0313

 1185/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 381us/step - acc: 0.9867 - loss: 0.0331

 1312/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 382us/step - acc: 0.9865 - loss: 0.0347

 1440/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 383us/step - acc: 0.9864 - loss: 0.0361

 1565/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 385us/step - acc: 0.9863 - loss: 0.0372

 1657/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 394us/step - acc: 0.9862 - loss: 0.0378

 1781/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 395us/step - acc: 0.9862 - loss: 0.0385

 1908/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 395us/step - acc: 0.9863 - loss: 0.0388

 2036/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 394us/step - acc: 0.9863 - loss: 0.0391

 2164/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 394us/step - acc: 0.9864 - loss: 0.0394

 2292/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 394us/step - acc: 0.9864 - loss: 0.0395

 2425/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 393us/step - acc: 0.9864 - loss: 0.0396

 2558/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 393us/step - acc: 0.9864 - loss: 0.0396

 2693/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 392us/step - acc: 0.9864 - loss: 0.0396

 2830/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 390us/step - acc: 0.9864 - loss: 0.0397

 2965/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 390us/step - acc: 0.9864 - loss: 0.0397

 3101/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 389us/step - acc: 0.9864 - loss: 0.0398

 3233/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 388us/step - acc: 0.9864 - loss: 0.0397

 3367/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 388us/step - acc: 0.9865 - loss: 0.0397

 3503/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 387us/step - acc: 0.9865 - loss: 0.0396

 3640/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 386us/step - acc: 0.9865 - loss: 0.0396

 3777/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 385us/step - acc: 0.9866 - loss: 0.0395

 3914/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 385us/step - acc: 0.9866 - loss: 0.0395

 4051/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 384us/step - acc: 0.9866 - loss: 0.0395

 4188/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 384us/step - acc: 0.9866 - loss: 0.0395

 4317/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 384us/step - acc: 0.9866 - loss: 0.0395

 4454/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 383us/step - acc: 0.9866 - loss: 0.0395

 4591/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 383us/step - acc: 0.9866 - loss: 0.0395

 4720/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 383us/step - acc: 0.9866 - loss: 0.0395

 4851/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 383us/step - acc: 0.9866 - loss: 0.0395

 4988/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 383us/step - acc: 0.9866 - loss: 0.0395

 5105/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 384us/step - acc: 0.9866 - loss: 0.0394

 5229/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 384us/step - acc: 0.9865 - loss: 0.0394

 5353/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 385us/step - acc: 0.9865 - loss: 0.0394

 5479/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 385us/step - acc: 0.9865 - loss: 0.0394

 5605/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 385us/step - acc: 0.9865 - loss: 0.0393

 5732/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 385us/step - acc: 0.9865 - loss: 0.0393

 5861/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 385us/step - acc: 0.9865 - loss: 0.0393

 5991/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 385us/step - acc: 0.9865 - loss: 0.0392

 6119/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 386us/step - acc: 0.9866 - loss: 0.0392

 6248/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 386us/step - acc: 0.9866 - loss: 0.0391

 6375/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 386us/step - acc: 0.9866 - loss: 0.0391

 6510/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 386us/step - acc: 0.9866 - loss: 0.0390

 6634/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 386us/step - acc: 0.9866 - loss: 0.0389

 6759/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 386us/step - acc: 0.9866 - loss: 0.0389

 6880/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 387us/step - acc: 0.9866 - loss: 0.0388

 6998/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 387us/step - acc: 0.9867 - loss: 0.0387

 7125/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 388us/step - acc: 0.9867 - loss: 0.0387

 7249/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 388us/step - acc: 0.9867 - loss: 0.0387

 7373/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 388us/step - acc: 0.9867 - loss: 0.0386

 7500/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 388us/step - acc: 0.9867 - loss: 0.0386

 7635/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 388us/step - acc: 0.9867 - loss: 0.0385

 7768/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 388us/step - acc: 0.9867 - loss: 0.0385

 7898/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 388us/step - acc: 0.9868 - loss: 0.0385

 8032/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 387us/step - acc: 0.9868 - loss: 0.0384

 8157/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 388us/step - acc: 0.9868 - loss: 0.0384

 8300/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 387us/step - acc: 0.9868 - loss: 0.0383

 8429/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 387us/step - acc: 0.9868 - loss: 0.0382

 8554/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 387us/step - acc: 0.9868 - loss: 0.0382

 8679/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 387us/step - acc: 0.9868 - loss: 0.0381

 8804/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 388us/step - acc: 0.9868 - loss: 0.0381

 8931/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 388us/step - acc: 0.9869 - loss: 0.0380

 9054/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 388us/step - acc: 0.9869 - loss: 0.0380

 9160/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 389us/step - acc: 0.9869 - loss: 0.0380

 9187/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 394us/step - acc: 0.9869 - loss: 0.0379

 9190/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 400us/step - acc: 0.9869 - loss: 0.0379

 9227/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 404us/step - acc: 0.9869 - loss: 0.0379

 9353/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 404us/step - acc: 0.9869 - loss: 0.0379

 9482/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 403us/step - acc: 0.9869 - loss: 0.0378

 9609/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 403us/step - acc: 0.9869 - loss: 0.0378

 9732/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 403us/step - acc: 0.9869 - loss: 0.0377

 9862/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 403us/step - acc: 0.9870 - loss: 0.0376

 9991/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 403us/step - acc: 0.9870 - loss: 0.0376

10128/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 403us/step - acc: 0.9870 - loss: 0.0375

10264/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 402us/step - acc: 0.9870 - loss: 0.0374

10400/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 402us/step - acc: 0.9870 - loss: 0.0374

10537/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 401us/step - acc: 0.9870 - loss: 0.0373

10667/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 401us/step - acc: 0.9871 - loss: 0.0373

10793/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 401us/step - acc: 0.9871 - loss: 0.0372

10919/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 401us/step - acc: 0.9871 - loss: 0.0372

11051/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 401us/step - acc: 0.9871 - loss: 0.0371

11189/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 400us/step - acc: 0.9871 - loss: 0.0371

11326/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 400us/step - acc: 0.9871 - loss: 0.0370

11461/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 400us/step - acc: 0.9871 - loss: 0.0370

11602/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 399us/step - acc: 0.9872 - loss: 0.0369

11731/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 399us/step - acc: 0.9872 - loss: 0.0369

11864/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 399us/step - acc: 0.9872 - loss: 0.0368

12000/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 398us/step - acc: 0.9872 - loss: 0.0368

12138/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 398us/step - acc: 0.9872 - loss: 0.0367

12275/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 398us/step - acc: 0.9872 - loss: 0.0367

12400/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 398us/step - acc: 0.9872 - loss: 0.0367

12523/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 398us/step - acc: 0.9872 - loss: 0.0366

12650/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 398us/step - acc: 0.9872 - loss: 0.0366

12781/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 398us/step - acc: 0.9872 - loss: 0.0366

12915/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 397us/step - acc: 0.9872 - loss: 0.0365

13051/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 397us/step - acc: 0.9873 - loss: 0.0365

13186/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 397us/step - acc: 0.9873 - loss: 0.0364

13324/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 396us/step - acc: 0.9873 - loss: 0.0364

13461/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 396us/step - acc: 0.9873 - loss: 0.0363

13598/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 396us/step - acc: 0.9873 - loss: 0.0363

13732/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 396us/step - acc: 0.9873 - loss: 0.0363

13869/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 395us/step - acc: 0.9873 - loss: 0.0362

14003/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 395us/step - acc: 0.9873 - loss: 0.0362

14138/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 395us/step - acc: 0.9873 - loss: 0.0361

14269/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 395us/step - acc: 0.9874 - loss: 0.0361

14398/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 395us/step - acc: 0.9874 - loss: 0.0360

14534/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 394us/step - acc: 0.9874 - loss: 0.0360

14670/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 394us/step - acc: 0.9874 - loss: 0.0360

14808/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 394us/step - acc: 0.9874 - loss: 0.0359

14947/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 394us/step - acc: 0.9874 - loss: 0.0359

15072/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 394us/step - acc: 0.9874 - loss: 0.0358

15205/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 394us/step - acc: 0.9874 - loss: 0.0358

15340/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 393us/step - acc: 0.9875 - loss: 0.0358

15469/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 393us/step - acc: 0.9875 - loss: 0.0357

15606/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 393us/step - acc: 0.9875 - loss: 0.0357

15743/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 393us/step - acc: 0.9875 - loss: 0.0357

15878/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 393us/step - acc: 0.9875 - loss: 0.0356

16002/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 393us/step - acc: 0.9875 - loss: 0.0356

16136/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 393us/step - acc: 0.9875 - loss: 0.0356

16275/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 392us/step - acc: 0.9875 - loss: 0.0356

16411/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 392us/step - acc: 0.9875 - loss: 0.0355

16548/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 392us/step - acc: 0.9875 - loss: 0.0355

16686/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 392us/step - acc: 0.9875 - loss: 0.0355

16825/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 391us/step - acc: 0.9875 - loss: 0.0355

16965/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 391us/step - acc: 0.9875 - loss: 0.0355

17105/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 391us/step - acc: 0.9875 - loss: 0.0355

17239/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 391us/step - acc: 0.9875 - loss: 0.0354

17378/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 391us/step - acc: 0.9875 - loss: 0.0354

17517/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 390us/step - acc: 0.9875 - loss: 0.0354

17656/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 390us/step - acc: 0.9876 - loss: 0.0354

17792/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 390us/step - acc: 0.9876 - loss: 0.0354

17930/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 390us/step - acc: 0.9876 - loss: 0.0353

18069/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 390us/step - acc: 0.9876 - loss: 0.0353

18206/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 389us/step - acc: 0.9876 - loss: 0.0353

18346/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 389us/step - acc: 0.9876 - loss: 0.0353

18486/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 389us/step - acc: 0.9876 - loss: 0.0353

18626/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 389us/step - acc: 0.9876 - loss: 0.0352

18768/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 388us/step - acc: 0.9876 - loss: 0.0352

18905/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 388us/step - acc: 0.9876 - loss: 0.0352

19043/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 388us/step - acc: 0.9876 - loss: 0.0352

19178/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 388us/step - acc: 0.9876 - loss: 0.0351

19315/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 388us/step - acc: 0.9876 - loss: 0.0351

19454/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 388us/step - acc: 0.9876 - loss: 0.0351

19590/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 387us/step - acc: 0.9876 - loss: 0.0351

19733/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 387us/step - acc: 0.9877 - loss: 0.0350

19866/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 387us/step - acc: 0.9877 - loss: 0.0350

19997/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 387us/step - acc: 0.9877 - loss: 0.0350

20134/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 387us/step - acc: 0.9877 - loss: 0.0350

20272/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 387us/step - acc: 0.9877 - loss: 0.0350

20406/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 387us/step - acc: 0.9877 - loss: 0.0349

20541/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 387us/step - acc: 0.9877 - loss: 0.0349

20680/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 386us/step - acc: 0.9877 - loss: 0.0349

20817/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 386us/step - acc: 0.9877 - loss: 0.0349

20953/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 386us/step - acc: 0.9877 - loss: 0.0349

21083/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 386us/step - acc: 0.9877 - loss: 0.0348

21223/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 386us/step - acc: 0.9877 - loss: 0.0348

21362/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 386us/step - acc: 0.9877 - loss: 0.0348

21501/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 386us/step - acc: 0.9877 - loss: 0.0348

21640/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 386us/step - acc: 0.9877 - loss: 0.0348

21777/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 385us/step - acc: 0.9877 - loss: 0.0347

21896/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 386us/step - acc: 0.9878 - loss: 0.0347

22030/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 386us/step - acc: 0.9878 - loss: 0.0347

22154/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 386us/step - acc: 0.9878 - loss: 0.0347

22282/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 386us/step - acc: 0.9878 - loss: 0.0347

22410/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 386us/step - acc: 0.9878 - loss: 0.0346

22543/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 386us/step - acc: 0.9878 - loss: 0.0346

22683/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 385us/step - acc: 0.9878 - loss: 0.0346

22824/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 385us/step - acc: 0.9878 - loss: 0.0346

22959/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 385us/step - acc: 0.9878 - loss: 0.0346

23065/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 386us/step - acc: 0.9878 - loss: 0.0345

23190/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 386us/step - acc: 0.9878 - loss: 0.0345

23315/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 386us/step - acc: 0.9878 - loss: 0.0345

23440/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 386us/step - acc: 0.9878 - loss: 0.0345

23567/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 386us/step - acc: 0.9878 - loss: 0.0345

23684/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 386us/step - acc: 0.9878 - loss: 0.0344

23810/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 386us/step - acc: 0.9879 - loss: 0.0344

23941/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 386us/step - acc: 0.9879 - loss: 0.0344

24069/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 386us/step - acc: 0.9879 - loss: 0.0344

24200/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 386us/step - acc: 0.9879 - loss: 0.0344

24310/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 387us/step - acc: 0.9879 - loss: 0.0343

24388/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 387us/step - acc: 0.9879 - loss: 0.0343

24486/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 388us/step - acc: 0.9879 - loss: 0.0343

24604/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 388us/step - acc: 0.9879 - loss: 0.0343

24720/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 388us/step - acc: 0.9879 - loss: 0.0343

24837/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 388us/step - acc: 0.9879 - loss: 0.0343

24954/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 389us/step - acc: 0.9879 - loss: 0.0342

25081/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 389us/step - acc: 0.9879 - loss: 0.0342

25208/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 389us/step - acc: 0.9879 - loss: 0.0342

25324/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 389us/step - acc: 0.9879 - loss: 0.0342

25414/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 390us/step - acc: 0.9879 - loss: 0.0342

25462/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 391us/step - acc: 0.9879 - loss: 0.0342

25486/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 392us/step - acc: 0.9879 - loss: 0.0342

25590/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 393us/step - acc: 0.9879 - loss: 0.0341

25695/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 393us/step - acc: 0.9879 - loss: 0.0341

25786/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 394us/step - acc: 0.9880 - loss: 0.0341

25870/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 394us/step - acc: 0.9880 - loss: 0.0341

25942/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 395us/step - acc: 0.9880 - loss: 0.0341

26008/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 396us/step - acc: 0.9880 - loss: 0.0341

26103/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 397us/step - acc: 0.9880 - loss: 0.0341

26193/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 397us/step - acc: 0.9880 - loss: 0.0341

26302/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 398us/step - acc: 0.9880 - loss: 0.0341

26405/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 398us/step - acc: 0.9880 - loss: 0.0340

26510/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 398us/step - acc: 0.9880 - loss: 0.0340

26620/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 399us/step - acc: 0.9880 - loss: 0.0340

26711/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 399us/step - acc: 0.9880 - loss: 0.0340

26809/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 399us/step - acc: 0.9880 - loss: 0.0340

26920/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 400us/step - acc: 0.9880 - loss: 0.0340

27035/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 400us/step - acc: 0.9880 - loss: 0.0340

27130/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 400us/step - acc: 0.9880 - loss: 0.0340

27244/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 400us/step - acc: 0.9880 - loss: 0.0339

27353/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 401us/step - acc: 0.9880 - loss: 0.0339

27459/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 401us/step - acc: 0.9880 - loss: 0.0339

27573/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 401us/step - acc: 0.9880 - loss: 0.0339

27688/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 401us/step - acc: 0.9880 - loss: 0.0339

27806/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 401us/step - acc: 0.9880 - loss: 0.0339

27921/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 402us/step - acc: 0.9880 - loss: 0.0339

28040/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 402us/step - acc: 0.9881 - loss: 0.0339

28126/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 402us/step - acc: 0.9881 - loss: 0.0338

28247/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 402us/step - acc: 0.9881 - loss: 0.0338

28344/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 403us/step - acc: 0.9881 - loss: 0.0338

28464/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 403us/step - acc: 0.9881 - loss: 0.0338

28573/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 403us/step - acc: 0.9881 - loss: 0.0338

28691/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 403us/step - acc: 0.9881 - loss: 0.0338

28814/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 403us/step - acc: 0.9881 - loss: 0.0338

28926/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 403us/step - acc: 0.9881 - loss: 0.0338

29046/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 403us/step - acc: 0.9881 - loss: 0.0337

29167/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 403us/step - acc: 0.9881 - loss: 0.0337

29284/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 403us/step - acc: 0.9881 - loss: 0.0337

29401/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 404us/step - acc: 0.9881 - loss: 0.0337

29521/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 404us/step - acc: 0.9881 - loss: 0.0337

29640/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 404us/step - acc: 0.9881 - loss: 0.0337

29756/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 404us/step - acc: 0.9881 - loss: 0.0337

29876/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 404us/step - acc: 0.9881 - loss: 0.0337

29972/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 404us/step - acc: 0.9881 - loss: 0.0336

30057/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 405us/step - acc: 0.9881 - loss: 0.0336

30166/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 405us/step - acc: 0.9881 - loss: 0.0336

30275/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 405us/step - acc: 0.9882 - loss: 0.0336

30393/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 405us/step - acc: 0.9882 - loss: 0.0336

30506/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 405us/step - acc: 0.9882 - loss: 0.0336

30591/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 406us/step - acc: 0.9882 - loss: 0.0336

30691/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 406us/step - acc: 0.9882 - loss: 0.0336

30782/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 407us/step - acc: 0.9882 - loss: 0.0336

30876/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 407us/step - acc: 0.9882 - loss: 0.0336

30969/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 407us/step - acc: 0.9882 - loss: 0.0335

31046/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 408us/step - acc: 0.9882 - loss: 0.0335

31091/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 409us/step - acc: 0.9882 - loss: 0.0335

31187/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 409us/step - acc: 0.9882 - loss: 0.0335

31300/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 410us/step - acc: 0.9882 - loss: 0.0335

31392/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 410us/step - acc: 0.9882 - loss: 0.0335

31448/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.9882 - loss: 0.0335

31534/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 411us/step - acc: 0.9882 - loss: 0.0335

31638/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 412us/step - acc: 0.9882 - loss: 0.0335

31733/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 412us/step - acc: 0.9882 - loss: 0.0335

31836/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 412us/step - acc: 0.9882 - loss: 0.0334

31947/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 412us/step - acc: 0.9882 - loss: 0.0334

32045/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 413us/step - acc: 0.9882 - loss: 0.0334

32133/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 413us/step - acc: 0.9882 - loss: 0.0334

32236/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 413us/step - acc: 0.9882 - loss: 0.0334

32343/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 413us/step - acc: 0.9882 - loss: 0.0334

32432/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 414us/step - acc: 0.9882 - loss: 0.0334

32538/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 414us/step - acc: 0.9883 - loss: 0.0334

32654/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 414us/step - acc: 0.9883 - loss: 0.0334

32769/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 414us/step - acc: 0.9883 - loss: 0.0333

32889/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 414us/step - acc: 0.9883 - loss: 0.0333

32979/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 415us/step - acc: 0.9883 - loss: 0.0333

33095/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 415us/step - acc: 0.9883 - loss: 0.0333

33208/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 415us/step - acc: 0.9883 - loss: 0.0333

33334/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 415us/step - acc: 0.9883 - loss: 0.0333

33461/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 415us/step - acc: 0.9883 - loss: 0.0333

33575/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 415us/step - acc: 0.9883 - loss: 0.0333

33701/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 415us/step - acc: 0.9883 - loss: 0.0332

33817/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 415us/step - acc: 0.9883 - loss: 0.0332

33924/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 415us/step - acc: 0.9883 - loss: 0.0332

34039/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 415us/step - acc: 0.9883 - loss: 0.0332

34127/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 415us/step - acc: 0.9883 - loss: 0.0332

34225/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 416us/step - acc: 0.9883 - loss: 0.0332

34319/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 416us/step - acc: 0.9883 - loss: 0.0332

34428/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 416us/step - acc: 0.9883 - loss: 0.0332

34549/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 416us/step - acc: 0.9883 - loss: 0.0331

34659/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 416us/step - acc: 0.9883 - loss: 0.0331

34783/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 416us/step - acc: 0.9883 - loss: 0.0331

34902/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 416us/step - acc: 0.9884 - loss: 0.0331

35035/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 416us/step - acc: 0.9884 - loss: 0.0331

35159/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 416us/step - acc: 0.9884 - loss: 0.0331

35257/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 416us/step - acc: 0.9884 - loss: 0.0331

35345/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 417us/step - acc: 0.9884 - loss: 0.0330

35420/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 417us/step - acc: 0.9884 - loss: 0.0330

35488/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 418us/step - acc: 0.9884 - loss: 0.0330

35579/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 418us/step - acc: 0.9884 - loss: 0.0330

35665/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 419us/step - acc: 0.9884 - loss: 0.0330

35776/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 419us/step - acc: 0.9884 - loss: 0.0330

35881/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 419us/step - acc: 0.9884 - loss: 0.0330

35980/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 419us/step - acc: 0.9884 - loss: 0.0330

36096/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 419us/step - acc: 0.9884 - loss: 0.0330

36190/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 420us/step - acc: 0.9884 - loss: 0.0329 

36299/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 420us/step - acc: 0.9884 - loss: 0.0329

36400/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 420us/step - acc: 0.9884 - loss: 0.0329

36510/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 420us/step - acc: 0.9884 - loss: 0.0329

36602/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 420us/step - acc: 0.9884 - loss: 0.0329

36683/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 421us/step - acc: 0.9884 - loss: 0.0329

36803/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 421us/step - acc: 0.9884 - loss: 0.0329

36921/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 421us/step - acc: 0.9884 - loss: 0.0329

37042/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 421us/step - acc: 0.9884 - loss: 0.0329

37154/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 421us/step - acc: 0.9885 - loss: 0.0328

37266/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 421us/step - acc: 0.9885 - loss: 0.0328

37386/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 421us/step - acc: 0.9885 - loss: 0.0328

37507/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 421us/step - acc: 0.9885 - loss: 0.0328

37634/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 421us/step - acc: 0.9885 - loss: 0.0328

37755/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 421us/step - acc: 0.9885 - loss: 0.0328

37871/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 421us/step - acc: 0.9885 - loss: 0.0328

37963/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 421us/step - acc: 0.9885 - loss: 0.0328

38070/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 421us/step - acc: 0.9885 - loss: 0.0328

38186/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 421us/step - acc: 0.9885 - loss: 0.0327

38302/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 421us/step - acc: 0.9885 - loss: 0.0327

38423/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 421us/step - acc: 0.9885 - loss: 0.0327

38541/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 421us/step - acc: 0.9885 - loss: 0.0327

38653/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 422us/step - acc: 0.9885 - loss: 0.0327

38756/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 422us/step - acc: 0.9885 - loss: 0.0327

38875/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 422us/step - acc: 0.9885 - loss: 0.0327

38988/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 422us/step - acc: 0.9885 - loss: 0.0327

39107/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 422us/step - acc: 0.9885 - loss: 0.0327

39229/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 422us/step - acc: 0.9885 - loss: 0.0326

39350/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 422us/step - acc: 0.9885 - loss: 0.0326

39477/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 422us/step - acc: 0.9885 - loss: 0.0326

39601/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 422us/step - acc: 0.9885 - loss: 0.0326

39716/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 422us/step - acc: 0.9886 - loss: 0.0326

39834/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 422us/step - acc: 0.9886 - loss: 0.0326

39960/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 422us/step - acc: 0.9886 - loss: 0.0326

40086/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 421us/step - acc: 0.9886 - loss: 0.0326

40214/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 421us/step - acc: 0.9886 - loss: 0.0326

40337/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 421us/step - acc: 0.9886 - loss: 0.0325

40463/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 421us/step - acc: 0.9886 - loss: 0.0325

40591/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 421us/step - acc: 0.9886 - loss: 0.0325

40722/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 421us/step - acc: 0.9886 - loss: 0.0325

40849/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 421us/step - acc: 0.9886 - loss: 0.0325

40979/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 421us/step - acc: 0.9886 - loss: 0.0325

41111/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 421us/step - acc: 0.9886 - loss: 0.0325

41243/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 421us/step - acc: 0.9886 - loss: 0.0325

41375/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 420us/step - acc: 0.9886 - loss: 0.0325

41503/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 420us/step - acc: 0.9886 - loss: 0.0325

41636/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 420us/step - acc: 0.9886 - loss: 0.0324

41770/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 420us/step - acc: 0.9886 - loss: 0.0324

41903/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 420us/step - acc: 0.9886 - loss: 0.0324

42028/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 420us/step - acc: 0.9886 - loss: 0.0324

42162/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 420us/step - acc: 0.9886 - loss: 0.0324

42297/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 420us/step - acc: 0.9886 - loss: 0.0324

42430/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 419us/step - acc: 0.9886 - loss: 0.0324

42560/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 419us/step - acc: 0.9886 - loss: 0.0324

42684/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 419us/step - acc: 0.9886 - loss: 0.0324

42809/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 419us/step - acc: 0.9886 - loss: 0.0324

42886/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 420us/step - acc: 0.9887 - loss: 0.0324

43008/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 420us/step - acc: 0.9887 - loss: 0.0324

43129/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 420us/step - acc: 0.9887 - loss: 0.0323

43253/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 420us/step - acc: 0.9887 - loss: 0.0323

43373/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 420us/step - acc: 0.9887 - loss: 0.0323

43497/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 420us/step - acc: 0.9887 - loss: 0.0323

43626/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 420us/step - acc: 0.9887 - loss: 0.0323

43756/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 419us/step - acc: 0.9887 - loss: 0.0323

43884/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 419us/step - acc: 0.9887 - loss: 0.0323

44003/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 419us/step - acc: 0.9887 - loss: 0.0323

44126/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 419us/step - acc: 0.9887 - loss: 0.0323

44260/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 419us/step - acc: 0.9887 - loss: 0.0323

44398/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 419us/step - acc: 0.9887 - loss: 0.0323

44530/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 419us/step - acc: 0.9887 - loss: 0.0323

44665/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 419us/step - acc: 0.9887 - loss: 0.0322

44802/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 419us/step - acc: 0.9887 - loss: 0.0322

44937/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 418us/step - acc: 0.9887 - loss: 0.0322

45070/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 418us/step - acc: 0.9887 - loss: 0.0322

45200/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 418us/step - acc: 0.9887 - loss: 0.0322

45325/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 418us/step - acc: 0.9887 - loss: 0.0322

45448/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 418us/step - acc: 0.9887 - loss: 0.0322

45571/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 418us/step - acc: 0.9887 - loss: 0.0322

45700/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 418us/step - acc: 0.9887 - loss: 0.0322

45824/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 418us/step - acc: 0.9887 - loss: 0.0322

45954/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 418us/step - acc: 0.9887 - loss: 0.0322

46087/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 418us/step - acc: 0.9887 - loss: 0.0322

46209/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 418us/step - acc: 0.9887 - loss: 0.0322

46343/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 418us/step - acc: 0.9887 - loss: 0.0322

46479/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 418us/step - acc: 0.9887 - loss: 0.0322

46601/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 418us/step - acc: 0.9887 - loss: 0.0321

46739/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 417us/step - acc: 0.9887 - loss: 0.0321

46873/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 417us/step - acc: 0.9888 - loss: 0.0321

47006/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 417us/step - acc: 0.9888 - loss: 0.0321

47145/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 417us/step - acc: 0.9888 - loss: 0.0321

47285/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 417us/step - acc: 0.9888 - loss: 0.0321

47425/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 417us/step - acc: 0.9888 - loss: 0.0321

47564/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 416us/step - acc: 0.9888 - loss: 0.0321

47708/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 416us/step - acc: 0.9888 - loss: 0.0321

47843/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 416us/step - acc: 0.9888 - loss: 0.0321

47981/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 416us/step - acc: 0.9888 - loss: 0.0321

48117/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 416us/step - acc: 0.9888 - loss: 0.0321

48247/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 416us/step - acc: 0.9888 - loss: 0.0321

48378/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 416us/step - acc: 0.9888 - loss: 0.0321

48506/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 416us/step - acc: 0.9888 - loss: 0.0321

48635/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 416us/step - acc: 0.9888 - loss: 0.0321

48764/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9888 - loss: 0.0321

48898/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9888 - loss: 0.0320

49034/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9888 - loss: 0.0320

49172/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9888 - loss: 0.0320

49309/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9888 - loss: 0.0320

49438/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9888 - loss: 0.0320

49553/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9888 - loss: 0.0320

49654/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9888 - loss: 0.0320

49765/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9888 - loss: 0.0320

49888/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9888 - loss: 0.0320

50012/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9888 - loss: 0.0320

50133/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9888 - loss: 0.0320

50250/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 415us/step - acc: 0.9888 - loss: 0.0320

50371/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0320

50493/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0320

50617/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0320

50737/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0320

50858/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0320

50978/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0320

51102/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0320

51227/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0320

51350/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0320

51473/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0320

51597/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0320

51715/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0320

51834/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0320

51960/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0320

52086/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0320

52210/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0320

52335/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0319

52462/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0319

52581/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0319

52706/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 415us/step - acc: 0.9888 - loss: 0.0319

52819/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9888 - loss: 0.0319

52939/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9888 - loss: 0.0319

53056/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9888 - loss: 0.0319

53173/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9888 - loss: 0.0319

53295/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9888 - loss: 0.0319

53418/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9888 - loss: 0.0319

53545/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9888 - loss: 0.0319

53668/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9888 - loss: 0.0319

53789/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9888 - loss: 0.0319

53885/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9888 - loss: 0.0319

54002/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9888 - loss: 0.0319

54129/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9888 - loss: 0.0319

54231/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9888 - loss: 0.0319

54351/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9888 - loss: 0.0319

54467/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9888 - loss: 0.0319

54564/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9888 - loss: 0.0319

54660/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 416us/step - acc: 0.9888 - loss: 0.0319

54772/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 416us/step - acc: 0.9888 - loss: 0.0319

54896/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 416us/step - acc: 0.9888 - loss: 0.0319

55014/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 416us/step - acc: 0.9888 - loss: 0.0319

55105/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 416us/step - acc: 0.9889 - loss: 0.0319

55211/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 416us/step - acc: 0.9889 - loss: 0.0319

55313/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 416us/step - acc: 0.9889 - loss: 0.0319

55406/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 416us/step - acc: 0.9889 - loss: 0.0319

55510/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 417us/step - acc: 0.9889 - loss: 0.0319

55609/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 417us/step - acc: 0.9889 - loss: 0.0319

55727/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 417us/step - acc: 0.9889 - loss: 0.0319

55846/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 417us/step - acc: 0.9889 - loss: 0.0319

55969/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 417us/step - acc: 0.9889 - loss: 0.0319

56083/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 417us/step - acc: 0.9889 - loss: 0.0319

56209/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 417us/step - acc: 0.9889 - loss: 0.0319

56334/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 417us/step - acc: 0.9889 - loss: 0.0319

56458/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 417us/step - acc: 0.9889 - loss: 0.0319

56570/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 417us/step - acc: 0.9889 - loss: 0.0319

56642/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 417us/step - acc: 0.9889 - loss: 0.0319

56712/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 417us/step - acc: 0.9889 - loss: 0.0319

56799/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 418us/step - acc: 0.9889 - loss: 0.0319

56910/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 418us/step - acc: 0.9889 - loss: 0.0319

56999/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 418us/step - acc: 0.9889 - loss: 0.0319

57110/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 418us/step - acc: 0.9889 - loss: 0.0319

57224/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 418us/step - acc: 0.9889 - loss: 0.0319

57324/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 418us/step - acc: 0.9889 - loss: 0.0319

57409/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 419us/step - acc: 0.9889 - loss: 0.0319

57531/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 419us/step - acc: 0.9889 - loss: 0.0319

57639/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 419us/step - acc: 0.9889 - loss: 0.0319

57754/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 419us/step - acc: 0.9889 - loss: 0.0319

57818/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 419us/step - acc: 0.9889 - loss: 0.0319

57832/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 420us/step - acc: 0.9889 - loss: 0.0319

57866/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 420us/step - acc: 0.9889 - loss: 0.0319

57971/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 421us/step - acc: 0.9889 - loss: 0.0319

58063/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 421us/step - acc: 0.9889 - loss: 0.0318

58167/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 421us/step - acc: 0.9889 - loss: 0.0318

58275/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 421us/step - acc: 0.9889 - loss: 0.0318

58390/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 421us/step - acc: 0.9889 - loss: 0.0318

58507/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 421us/step - acc: 0.9889 - loss: 0.0318

58622/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 421us/step - acc: 0.9889 - loss: 0.0318

58748/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 421us/step - acc: 0.9889 - loss: 0.0318

58869/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 421us/step - acc: 0.9889 - loss: 0.0318

58984/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 421us/step - acc: 0.9889 - loss: 0.0318

59101/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 421us/step - acc: 0.9889 - loss: 0.0318

59172/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 421us/step - acc: 0.9889 - loss: 0.0318

59264/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 422us/step - acc: 0.9889 - loss: 0.0318

59365/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 422us/step - acc: 0.9889 - loss: 0.0318

59458/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 422us/step - acc: 0.9889 - loss: 0.0318

59549/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 422us/step - acc: 0.9889 - loss: 0.0318

59653/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 422us/step - acc: 0.9889 - loss: 0.0318

59760/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 422us/step - acc: 0.9889 - loss: 0.0318

59848/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 422us/step - acc: 0.9889 - loss: 0.0318

59901/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 423us/step - acc: 0.9889 - loss: 0.0318

59980/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 423us/step - acc: 0.9889 - loss: 0.0318

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 30s 492us/step - acc: 0.9889 - loss: 0.0318 - val_acc: 0.9709 - val_loss: 0.1177

Epoch 19/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 14:31 15ms/step - acc: 1.0000 - loss: 7.1526e-07

  121/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 417us/step - acc: 1.0000 - loss: 0.0070     

  249/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 404us/step - acc: 1.0000 - loss: 0.0053

  385/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 392us/step - acc: 1.0000 - loss: 0.0050

  521/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 386us/step - acc: 0.9997 - loss: 0.0057

  658/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 382us/step - acc: 0.9994 - loss: 0.0067

  781/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 386us/step - acc: 0.9991 - loss: 0.0075

  913/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 386us/step - acc: 0.9989 - loss: 0.0082

 1016/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 396us/step - acc: 0.9987 - loss: 0.0088

 1134/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 399us/step - acc: 0.9984 - loss: 0.0098

 1265/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 397us/step - acc: 0.9981 - loss: 0.0107

 1392/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 397us/step - acc: 0.9978 - loss: 0.0114

 1514/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 398us/step - acc: 0.9975 - loss: 0.0120

 1627/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 401us/step - acc: 0.9973 - loss: 0.0126

 1745/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 403us/step - acc: 0.9970 - loss: 0.0131

 1855/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 406us/step - acc: 0.9969 - loss: 0.0134

 1969/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 408us/step - acc: 0.9967 - loss: 0.0138

 2082/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 410us/step - acc: 0.9965 - loss: 0.0143

 2195/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 412us/step - acc: 0.9963 - loss: 0.0147

 2312/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 413us/step - acc: 0.9961 - loss: 0.0151

 2414/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 416us/step - acc: 0.9960 - loss: 0.0154

 2533/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 417us/step - acc: 0.9958 - loss: 0.0157

 2656/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 416us/step - acc: 0.9956 - loss: 0.0160

 2766/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 418us/step - acc: 0.9955 - loss: 0.0162

 2885/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 418us/step - acc: 0.9954 - loss: 0.0165

 3004/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 418us/step - acc: 0.9953 - loss: 0.0166

 3122/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 418us/step - acc: 0.9952 - loss: 0.0168

 3242/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 418us/step - acc: 0.9951 - loss: 0.0170

 3359/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 419us/step - acc: 0.9950 - loss: 0.0171

 3467/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 420us/step - acc: 0.9950 - loss: 0.0172

 3573/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 422us/step - acc: 0.9949 - loss: 0.0173

 3693/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 422us/step - acc: 0.9949 - loss: 0.0174

 3816/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 422us/step - acc: 0.9948 - loss: 0.0176

 3948/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 420us/step - acc: 0.9947 - loss: 0.0177

 4072/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 420us/step - acc: 0.9947 - loss: 0.0178

 4206/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 418us/step - acc: 0.9947 - loss: 0.0178

 4332/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 418us/step - acc: 0.9946 - loss: 0.0179

 4455/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 417us/step - acc: 0.9946 - loss: 0.0180

 4579/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 417us/step - acc: 0.9945 - loss: 0.0180

 4710/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 416us/step - acc: 0.9945 - loss: 0.0181

 4839/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 415us/step - acc: 0.9945 - loss: 0.0182

 4980/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 414us/step - acc: 0.9944 - loss: 0.0183

 5112/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 413us/step - acc: 0.9944 - loss: 0.0183

 5247/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 412us/step - acc: 0.9944 - loss: 0.0184

 5372/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 412us/step - acc: 0.9944 - loss: 0.0184

 5507/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 411us/step - acc: 0.9943 - loss: 0.0185

 5647/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 409us/step - acc: 0.9943 - loss: 0.0185

 5782/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 408us/step - acc: 0.9942 - loss: 0.0186

 5918/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 407us/step - acc: 0.9942 - loss: 0.0186

 6051/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 407us/step - acc: 0.9942 - loss: 0.0187

 6180/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 406us/step - acc: 0.9941 - loss: 0.0188

 6311/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 406us/step - acc: 0.9941 - loss: 0.0188

 6442/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 405us/step - acc: 0.9941 - loss: 0.0189

 6568/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 405us/step - acc: 0.9940 - loss: 0.0190

 6696/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 405us/step - acc: 0.9940 - loss: 0.0190

 6826/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 405us/step - acc: 0.9940 - loss: 0.0191

 6953/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 405us/step - acc: 0.9939 - loss: 0.0192

 7083/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 404us/step - acc: 0.9939 - loss: 0.0192

 7221/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 403us/step - acc: 0.9939 - loss: 0.0193

 7348/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 403us/step - acc: 0.9938 - loss: 0.0193

 7485/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 403us/step - acc: 0.9938 - loss: 0.0194

 7623/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 402us/step - acc: 0.9938 - loss: 0.0195

 7758/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 401us/step - acc: 0.9937 - loss: 0.0196

 7893/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 401us/step - acc: 0.9937 - loss: 0.0197

 8028/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 400us/step - acc: 0.9937 - loss: 0.0198

 8162/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 400us/step - acc: 0.9936 - loss: 0.0199

 8291/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 400us/step - acc: 0.9936 - loss: 0.0200

 8420/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 400us/step - acc: 0.9936 - loss: 0.0201

 8557/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 399us/step - acc: 0.9935 - loss: 0.0202

 8669/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 400us/step - acc: 0.9935 - loss: 0.0202

 8800/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 399us/step - acc: 0.9935 - loss: 0.0203

 8933/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 399us/step - acc: 0.9934 - loss: 0.0204

 9069/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 399us/step - acc: 0.9934 - loss: 0.0204

 9202/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 398us/step - acc: 0.9934 - loss: 0.0205

 9338/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 398us/step - acc: 0.9934 - loss: 0.0206

 9474/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 398us/step - acc: 0.9933 - loss: 0.0206

 9613/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 397us/step - acc: 0.9933 - loss: 0.0207

 9749/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 397us/step - acc: 0.9933 - loss: 0.0207

 9887/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 396us/step - acc: 0.9933 - loss: 0.0208

10027/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 396us/step - acc: 0.9932 - loss: 0.0209

10165/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 395us/step - acc: 0.9932 - loss: 0.0209

10301/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 395us/step - acc: 0.9932 - loss: 0.0210

10437/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 395us/step - acc: 0.9932 - loss: 0.0211

10574/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 394us/step - acc: 0.9931 - loss: 0.0211

10703/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 394us/step - acc: 0.9931 - loss: 0.0212

10841/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 394us/step - acc: 0.9931 - loss: 0.0213

10966/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 394us/step - acc: 0.9931 - loss: 0.0213

11092/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 394us/step - acc: 0.9930 - loss: 0.0214

11214/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 394us/step - acc: 0.9930 - loss: 0.0214

11335/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 394us/step - acc: 0.9930 - loss: 0.0214

11461/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 394us/step - acc: 0.9930 - loss: 0.0215

11588/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 394us/step - acc: 0.9930 - loss: 0.0215

11726/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 394us/step - acc: 0.9930 - loss: 0.0216

11853/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 394us/step - acc: 0.9929 - loss: 0.0216

11976/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 394us/step - acc: 0.9929 - loss: 0.0217

12091/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 395us/step - acc: 0.9929 - loss: 0.0217

12205/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 395us/step - acc: 0.9929 - loss: 0.0217

12327/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 395us/step - acc: 0.9929 - loss: 0.0218

12448/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 395us/step - acc: 0.9929 - loss: 0.0218

12585/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 395us/step - acc: 0.9929 - loss: 0.0218

12724/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 395us/step - acc: 0.9929 - loss: 0.0219

12862/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 394us/step - acc: 0.9928 - loss: 0.0219

12996/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 394us/step - acc: 0.9928 - loss: 0.0220

13117/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 394us/step - acc: 0.9928 - loss: 0.0220

13243/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 394us/step - acc: 0.9928 - loss: 0.0220

13378/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 394us/step - acc: 0.9928 - loss: 0.0221

13501/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 394us/step - acc: 0.9928 - loss: 0.0221

13624/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 394us/step - acc: 0.9928 - loss: 0.0221

13761/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 394us/step - acc: 0.9928 - loss: 0.0221

13890/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 394us/step - acc: 0.9928 - loss: 0.0222

14008/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 394us/step - acc: 0.9927 - loss: 0.0222

14110/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 395us/step - acc: 0.9927 - loss: 0.0222

14227/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 395us/step - acc: 0.9927 - loss: 0.0222

14353/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 395us/step - acc: 0.9927 - loss: 0.0223

14477/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 396us/step - acc: 0.9927 - loss: 0.0223

14604/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 396us/step - acc: 0.9927 - loss: 0.0223

14738/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 395us/step - acc: 0.9927 - loss: 0.0224

14873/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 395us/step - acc: 0.9927 - loss: 0.0224

15009/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 395us/step - acc: 0.9927 - loss: 0.0224

15142/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 395us/step - acc: 0.9927 - loss: 0.0224

15289/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 394us/step - acc: 0.9926 - loss: 0.0225

15429/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 394us/step - acc: 0.9926 - loss: 0.0225

15564/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 394us/step - acc: 0.9926 - loss: 0.0225

15698/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 394us/step - acc: 0.9926 - loss: 0.0226

15835/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 393us/step - acc: 0.9926 - loss: 0.0226

15972/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 393us/step - acc: 0.9926 - loss: 0.0226

16107/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 393us/step - acc: 0.9926 - loss: 0.0227

16242/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 393us/step - acc: 0.9926 - loss: 0.0227

16381/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 392us/step - acc: 0.9926 - loss: 0.0227

16517/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 392us/step - acc: 0.9926 - loss: 0.0228

16644/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 392us/step - acc: 0.9925 - loss: 0.0228

16721/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 393us/step - acc: 0.9925 - loss: 0.0228

16849/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 393us/step - acc: 0.9925 - loss: 0.0229

16964/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 394us/step - acc: 0.9925 - loss: 0.0229

17079/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 394us/step - acc: 0.9925 - loss: 0.0229

17204/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 394us/step - acc: 0.9925 - loss: 0.0229

17330/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 394us/step - acc: 0.9925 - loss: 0.0230

17463/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 394us/step - acc: 0.9925 - loss: 0.0230

17601/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 394us/step - acc: 0.9925 - loss: 0.0230

17735/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 394us/step - acc: 0.9925 - loss: 0.0230

17873/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 393us/step - acc: 0.9925 - loss: 0.0231

18011/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 393us/step - acc: 0.9925 - loss: 0.0231

18142/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 393us/step - acc: 0.9925 - loss: 0.0231

18282/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 393us/step - acc: 0.9925 - loss: 0.0231

18424/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 393us/step - acc: 0.9924 - loss: 0.0232

18562/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 392us/step - acc: 0.9924 - loss: 0.0232

18703/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 392us/step - acc: 0.9924 - loss: 0.0232

18836/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 392us/step - acc: 0.9924 - loss: 0.0232

18972/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 392us/step - acc: 0.9924 - loss: 0.0233

19092/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 392us/step - acc: 0.9924 - loss: 0.0233

19228/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 392us/step - acc: 0.9924 - loss: 0.0233

19362/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 392us/step - acc: 0.9924 - loss: 0.0233

19496/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 392us/step - acc: 0.9924 - loss: 0.0234

19631/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 391us/step - acc: 0.9924 - loss: 0.0234

19768/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 391us/step - acc: 0.9924 - loss: 0.0234

19905/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 391us/step - acc: 0.9924 - loss: 0.0234

20043/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 391us/step - acc: 0.9924 - loss: 0.0234

20180/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 391us/step - acc: 0.9924 - loss: 0.0235

20316/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 391us/step - acc: 0.9924 - loss: 0.0235

20448/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 390us/step - acc: 0.9923 - loss: 0.0235

20583/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 390us/step - acc: 0.9923 - loss: 0.0235

20707/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 390us/step - acc: 0.9923 - loss: 0.0236

20839/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 390us/step - acc: 0.9923 - loss: 0.0236

20970/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 390us/step - acc: 0.9923 - loss: 0.0236

21108/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 390us/step - acc: 0.9923 - loss: 0.0236

21247/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 390us/step - acc: 0.9923 - loss: 0.0236

21382/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 390us/step - acc: 0.9923 - loss: 0.0236

21513/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 390us/step - acc: 0.9923 - loss: 0.0237

21647/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 390us/step - acc: 0.9923 - loss: 0.0237

21784/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 390us/step - acc: 0.9923 - loss: 0.0237

21918/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 390us/step - acc: 0.9923 - loss: 0.0237

22054/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 389us/step - acc: 0.9923 - loss: 0.0237

22191/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 389us/step - acc: 0.9923 - loss: 0.0237

22331/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 389us/step - acc: 0.9923 - loss: 0.0237

22468/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 389us/step - acc: 0.9923 - loss: 0.0238

22604/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 389us/step - acc: 0.9923 - loss: 0.0238

22714/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 389us/step - acc: 0.9923 - loss: 0.0238

22824/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 389us/step - acc: 0.9923 - loss: 0.0238

22938/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 390us/step - acc: 0.9923 - loss: 0.0238

23068/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 390us/step - acc: 0.9923 - loss: 0.0238

23199/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 390us/step - acc: 0.9923 - loss: 0.0238

23297/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 390us/step - acc: 0.9923 - loss: 0.0238

23412/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 390us/step - acc: 0.9922 - loss: 0.0238

23535/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 390us/step - acc: 0.9922 - loss: 0.0238

23661/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 391us/step - acc: 0.9922 - loss: 0.0239

23789/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 391us/step - acc: 0.9922 - loss: 0.0239

23915/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 391us/step - acc: 0.9922 - loss: 0.0239

24044/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 391us/step - acc: 0.9922 - loss: 0.0239

24172/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 391us/step - acc: 0.9922 - loss: 0.0239

24302/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 391us/step - acc: 0.9922 - loss: 0.0239

24429/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 391us/step - acc: 0.9922 - loss: 0.0239

24558/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 391us/step - acc: 0.9922 - loss: 0.0239

24685/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 391us/step - acc: 0.9922 - loss: 0.0239

24813/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 391us/step - acc: 0.9922 - loss: 0.0239

24941/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 391us/step - acc: 0.9922 - loss: 0.0239

25069/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 391us/step - acc: 0.9922 - loss: 0.0239

25203/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 390us/step - acc: 0.9922 - loss: 0.0239

25335/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 390us/step - acc: 0.9922 - loss: 0.0239

25469/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 390us/step - acc: 0.9922 - loss: 0.0240

25601/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 390us/step - acc: 0.9922 - loss: 0.0240

25733/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 390us/step - acc: 0.9922 - loss: 0.0240

25856/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 390us/step - acc: 0.9922 - loss: 0.0240

25984/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 390us/step - acc: 0.9922 - loss: 0.0240

26113/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 390us/step - acc: 0.9922 - loss: 0.0240

26245/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 390us/step - acc: 0.9922 - loss: 0.0240

26374/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 390us/step - acc: 0.9922 - loss: 0.0240

26508/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 390us/step - acc: 0.9922 - loss: 0.0240

26635/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 390us/step - acc: 0.9922 - loss: 0.0240

26762/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 390us/step - acc: 0.9922 - loss: 0.0240

26890/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 390us/step - acc: 0.9922 - loss: 0.0240

27009/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 390us/step - acc: 0.9922 - loss: 0.0240

27139/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 390us/step - acc: 0.9922 - loss: 0.0240

27262/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 390us/step - acc: 0.9922 - loss: 0.0241

27382/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 391us/step - acc: 0.9922 - loss: 0.0241

27504/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 391us/step - acc: 0.9922 - loss: 0.0241

27627/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 391us/step - acc: 0.9922 - loss: 0.0241

27752/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 391us/step - acc: 0.9922 - loss: 0.0241

27880/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 391us/step - acc: 0.9922 - loss: 0.0241

28012/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 391us/step - acc: 0.9922 - loss: 0.0241

28141/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 391us/step - acc: 0.9922 - loss: 0.0241

28268/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 391us/step - acc: 0.9922 - loss: 0.0241

28397/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 391us/step - acc: 0.9922 - loss: 0.0241

28527/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 391us/step - acc: 0.9922 - loss: 0.0241

28659/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 391us/step - acc: 0.9922 - loss: 0.0241

28790/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 391us/step - acc: 0.9922 - loss: 0.0241

28916/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 391us/step - acc: 0.9922 - loss: 0.0241

29046/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 391us/step - acc: 0.9922 - loss: 0.0241

29177/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 391us/step - acc: 0.9922 - loss: 0.0241

29309/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 391us/step - acc: 0.9922 - loss: 0.0241

29436/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 391us/step - acc: 0.9922 - loss: 0.0241

29562/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 391us/step - acc: 0.9922 - loss: 0.0241

29687/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 391us/step - acc: 0.9922 - loss: 0.0241

29818/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 391us/step - acc: 0.9922 - loss: 0.0241

29951/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 391us/step - acc: 0.9921 - loss: 0.0241

30086/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9921 - loss: 0.0241

30221/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9921 - loss: 0.0241

30351/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9921 - loss: 0.0241

30479/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9921 - loss: 0.0241

30612/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9921 - loss: 0.0241

30743/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9921 - loss: 0.0241

30870/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9921 - loss: 0.0241

30998/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 390us/step - acc: 0.9921 - loss: 0.0241

31041/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 391us/step - acc: 0.9921 - loss: 0.0241

31108/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 392us/step - acc: 0.9921 - loss: 0.0241

31197/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 393us/step - acc: 0.9921 - loss: 0.0241

31253/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 394us/step - acc: 0.9921 - loss: 0.0241

31332/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 394us/step - acc: 0.9921 - loss: 0.0241

31434/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 395us/step - acc: 0.9921 - loss: 0.0241

31500/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 395us/step - acc: 0.9921 - loss: 0.0241

31575/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 396us/step - acc: 0.9921 - loss: 0.0241

31662/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 396us/step - acc: 0.9921 - loss: 0.0241

31768/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 397us/step - acc: 0.9921 - loss: 0.0241

31881/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 397us/step - acc: 0.9921 - loss: 0.0241

31979/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 397us/step - acc: 0.9921 - loss: 0.0242

32068/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 398us/step - acc: 0.9921 - loss: 0.0242

32162/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 398us/step - acc: 0.9921 - loss: 0.0242

32256/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 399us/step - acc: 0.9921 - loss: 0.0242

32368/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 399us/step - acc: 0.9921 - loss: 0.0242

32486/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 399us/step - acc: 0.9921 - loss: 0.0242

32608/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 399us/step - acc: 0.9921 - loss: 0.0242

32710/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 399us/step - acc: 0.9921 - loss: 0.0242

32795/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 400us/step - acc: 0.9921 - loss: 0.0242

32897/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 400us/step - acc: 0.9921 - loss: 0.0242

33021/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 400us/step - acc: 0.9921 - loss: 0.0242

33150/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 400us/step - acc: 0.9921 - loss: 0.0242

33281/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 400us/step - acc: 0.9921 - loss: 0.0242

33404/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 400us/step - acc: 0.9921 - loss: 0.0242

33534/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 400us/step - acc: 0.9921 - loss: 0.0242

33665/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 400us/step - acc: 0.9921 - loss: 0.0242

33794/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 400us/step - acc: 0.9921 - loss: 0.0242

33925/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 400us/step - acc: 0.9921 - loss: 0.0242

34063/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 400us/step - acc: 0.9921 - loss: 0.0242

34194/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 399us/step - acc: 0.9921 - loss: 0.0242

34326/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 399us/step - acc: 0.9921 - loss: 0.0242

34460/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 399us/step - acc: 0.9921 - loss: 0.0242

34594/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 399us/step - acc: 0.9921 - loss: 0.0242

34730/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 399us/step - acc: 0.9921 - loss: 0.0242

34864/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 399us/step - acc: 0.9921 - loss: 0.0242

35002/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 399us/step - acc: 0.9921 - loss: 0.0242 

35125/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 399us/step - acc: 0.9921 - loss: 0.0242

35252/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 399us/step - acc: 0.9921 - loss: 0.0242

35375/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 399us/step - acc: 0.9921 - loss: 0.0242

35504/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 399us/step - acc: 0.9921 - loss: 0.0242

35634/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 399us/step - acc: 0.9921 - loss: 0.0242

35773/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 399us/step - acc: 0.9921 - loss: 0.0242

35911/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 399us/step - acc: 0.9921 - loss: 0.0242

36047/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 398us/step - acc: 0.9921 - loss: 0.0242

36171/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 398us/step - acc: 0.9921 - loss: 0.0242

36294/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 398us/step - acc: 0.9921 - loss: 0.0242

36420/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 398us/step - acc: 0.9921 - loss: 0.0242

36550/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 398us/step - acc: 0.9921 - loss: 0.0242

36682/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 398us/step - acc: 0.9921 - loss: 0.0242

36820/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 398us/step - acc: 0.9921 - loss: 0.0242

36960/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 398us/step - acc: 0.9921 - loss: 0.0242

37093/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 398us/step - acc: 0.9921 - loss: 0.0242

37227/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 398us/step - acc: 0.9921 - loss: 0.0242

37366/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 398us/step - acc: 0.9921 - loss: 0.0242

37503/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 398us/step - acc: 0.9921 - loss: 0.0242

37639/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 398us/step - acc: 0.9921 - loss: 0.0242

37776/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 397us/step - acc: 0.9921 - loss: 0.0242

37913/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 397us/step - acc: 0.9921 - loss: 0.0242

38048/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 397us/step - acc: 0.9921 - loss: 0.0242

38176/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 397us/step - acc: 0.9921 - loss: 0.0242

38308/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 397us/step - acc: 0.9921 - loss: 0.0242

38436/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 397us/step - acc: 0.9921 - loss: 0.0242

38565/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 397us/step - acc: 0.9921 - loss: 0.0242

38698/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 397us/step - acc: 0.9921 - loss: 0.0242

38834/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 397us/step - acc: 0.9921 - loss: 0.0242

38971/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 397us/step - acc: 0.9921 - loss: 0.0242

39112/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 397us/step - acc: 0.9921 - loss: 0.0242

39250/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 397us/step - acc: 0.9921 - loss: 0.0242

39384/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 397us/step - acc: 0.9921 - loss: 0.0242

39520/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 396us/step - acc: 0.9921 - loss: 0.0242

39658/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 396us/step - acc: 0.9921 - loss: 0.0242

39795/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 396us/step - acc: 0.9921 - loss: 0.0242

39932/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 396us/step - acc: 0.9921 - loss: 0.0242

40070/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 396us/step - acc: 0.9921 - loss: 0.0242

40206/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 396us/step - acc: 0.9921 - loss: 0.0243

40345/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 396us/step - acc: 0.9921 - loss: 0.0243

40485/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 396us/step - acc: 0.9921 - loss: 0.0243

40624/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 396us/step - acc: 0.9921 - loss: 0.0243

40760/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 395us/step - acc: 0.9921 - loss: 0.0243

40897/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 395us/step - acc: 0.9921 - loss: 0.0243

41034/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 395us/step - acc: 0.9921 - loss: 0.0243

41172/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 395us/step - acc: 0.9921 - loss: 0.0243

41312/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 395us/step - acc: 0.9921 - loss: 0.0243

41452/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 395us/step - acc: 0.9921 - loss: 0.0243

41588/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 395us/step - acc: 0.9921 - loss: 0.0243

41722/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 395us/step - acc: 0.9921 - loss: 0.0243

41856/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 395us/step - acc: 0.9921 - loss: 0.0243

41991/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 395us/step - acc: 0.9921 - loss: 0.0243

42119/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 395us/step - acc: 0.9921 - loss: 0.0243

42250/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 395us/step - acc: 0.9921 - loss: 0.0243

42377/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 395us/step - acc: 0.9921 - loss: 0.0243

42500/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 395us/step - acc: 0.9921 - loss: 0.0243

42625/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 395us/step - acc: 0.9921 - loss: 0.0243

42743/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 395us/step - acc: 0.9921 - loss: 0.0243

42865/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 395us/step - acc: 0.9921 - loss: 0.0243

42988/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 395us/step - acc: 0.9921 - loss: 0.0243

43100/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 395us/step - acc: 0.9921 - loss: 0.0243

43224/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 395us/step - acc: 0.9921 - loss: 0.0243

43345/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 395us/step - acc: 0.9921 - loss: 0.0243

43468/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 395us/step - acc: 0.9921 - loss: 0.0243

43584/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 395us/step - acc: 0.9921 - loss: 0.0243

43712/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 395us/step - acc: 0.9921 - loss: 0.0243

43837/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 395us/step - acc: 0.9921 - loss: 0.0243

43946/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 395us/step - acc: 0.9921 - loss: 0.0243

44046/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 396us/step - acc: 0.9921 - loss: 0.0243

44158/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 396us/step - acc: 0.9921 - loss: 0.0243

44270/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 396us/step - acc: 0.9921 - loss: 0.0243

44378/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 396us/step - acc: 0.9921 - loss: 0.0243

44503/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 396us/step - acc: 0.9921 - loss: 0.0243

44630/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 396us/step - acc: 0.9921 - loss: 0.0243

44750/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 396us/step - acc: 0.9921 - loss: 0.0243

44871/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 396us/step - acc: 0.9921 - loss: 0.0243

44989/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 396us/step - acc: 0.9921 - loss: 0.0243

45112/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 396us/step - acc: 0.9921 - loss: 0.0243

45226/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 396us/step - acc: 0.9921 - loss: 0.0243

45342/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 396us/step - acc: 0.9921 - loss: 0.0243

45457/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 396us/step - acc: 0.9921 - loss: 0.0243

45584/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 396us/step - acc: 0.9921 - loss: 0.0243

45713/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 396us/step - acc: 0.9921 - loss: 0.0243

45841/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 396us/step - acc: 0.9921 - loss: 0.0243

45968/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 396us/step - acc: 0.9921 - loss: 0.0243

46098/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 396us/step - acc: 0.9921 - loss: 0.0243

46217/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 396us/step - acc: 0.9920 - loss: 0.0243

46341/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 397us/step - acc: 0.9920 - loss: 0.0243

46472/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 396us/step - acc: 0.9920 - loss: 0.0243

46596/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 397us/step - acc: 0.9920 - loss: 0.0243

46722/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 397us/step - acc: 0.9920 - loss: 0.0243

46849/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 397us/step - acc: 0.9920 - loss: 0.0243

46976/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 396us/step - acc: 0.9920 - loss: 0.0243

47101/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 397us/step - acc: 0.9920 - loss: 0.0243

47224/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 397us/step - acc: 0.9920 - loss: 0.0243

47354/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 397us/step - acc: 0.9920 - loss: 0.0243

47482/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 397us/step - acc: 0.9920 - loss: 0.0243

47603/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 397us/step - acc: 0.9920 - loss: 0.0243

47726/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 397us/step - acc: 0.9920 - loss: 0.0243

47847/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 397us/step - acc: 0.9920 - loss: 0.0243

47969/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 397us/step - acc: 0.9920 - loss: 0.0244

48067/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 397us/step - acc: 0.9920 - loss: 0.0244

48129/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 397us/step - acc: 0.9920 - loss: 0.0244

48189/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 398us/step - acc: 0.9920 - loss: 0.0244

48286/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 398us/step - acc: 0.9920 - loss: 0.0244

48342/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 399us/step - acc: 0.9920 - loss: 0.0244

48430/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 399us/step - acc: 0.9920 - loss: 0.0244

48521/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 399us/step - acc: 0.9920 - loss: 0.0244

48619/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 400us/step - acc: 0.9920 - loss: 0.0244

48696/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 400us/step - acc: 0.9920 - loss: 0.0244

48770/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 401us/step - acc: 0.9920 - loss: 0.0244

48862/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 401us/step - acc: 0.9920 - loss: 0.0244

48971/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 401us/step - acc: 0.9920 - loss: 0.0244

49075/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 401us/step - acc: 0.9920 - loss: 0.0244

49185/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 401us/step - acc: 0.9920 - loss: 0.0244

49294/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 401us/step - acc: 0.9920 - loss: 0.0244

49345/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 402us/step - acc: 0.9920 - loss: 0.0244

49446/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 402us/step - acc: 0.9920 - loss: 0.0244

49553/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 402us/step - acc: 0.9920 - loss: 0.0244

49654/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 403us/step - acc: 0.9920 - loss: 0.0244

49772/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 403us/step - acc: 0.9920 - loss: 0.0244

49892/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 403us/step - acc: 0.9920 - loss: 0.0244

49981/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 403us/step - acc: 0.9920 - loss: 0.0244

50091/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 403us/step - acc: 0.9920 - loss: 0.0244

50203/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 403us/step - acc: 0.9920 - loss: 0.0244

50315/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 403us/step - acc: 0.9920 - loss: 0.0244

50436/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 403us/step - acc: 0.9920 - loss: 0.0244

50538/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 403us/step - acc: 0.9920 - loss: 0.0244

50638/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.9920 - loss: 0.0244

50742/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.9920 - loss: 0.0244

50848/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.9920 - loss: 0.0244

50950/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.9920 - loss: 0.0245

51056/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.9920 - loss: 0.0245

51161/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 404us/step - acc: 0.9920 - loss: 0.0245

51262/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 405us/step - acc: 0.9920 - loss: 0.0245

51355/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 405us/step - acc: 0.9920 - loss: 0.0245

51455/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 405us/step - acc: 0.9920 - loss: 0.0245

51568/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 405us/step - acc: 0.9920 - loss: 0.0245

51694/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 405us/step - acc: 0.9920 - loss: 0.0245

51793/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 405us/step - acc: 0.9920 - loss: 0.0245

51871/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 406us/step - acc: 0.9920 - loss: 0.0245

51987/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 406us/step - acc: 0.9920 - loss: 0.0245

52098/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 406us/step - acc: 0.9920 - loss: 0.0245

52204/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 406us/step - acc: 0.9920 - loss: 0.0245

52290/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 406us/step - acc: 0.9920 - loss: 0.0245

52311/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 407us/step - acc: 0.9920 - loss: 0.0245

52331/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 408us/step - acc: 0.9920 - loss: 0.0245

52361/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 409us/step - acc: 0.9920 - loss: 0.0245

52436/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 409us/step - acc: 0.9920 - loss: 0.0245

52455/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 410us/step - acc: 0.9920 - loss: 0.0245

52476/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 411us/step - acc: 0.9920 - loss: 0.0245

52548/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 411us/step - acc: 0.9920 - loss: 0.0245

52622/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 412us/step - acc: 0.9920 - loss: 0.0245

52701/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 412us/step - acc: 0.9920 - loss: 0.0245

52778/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 412us/step - acc: 0.9920 - loss: 0.0245

52825/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 413us/step - acc: 0.9920 - loss: 0.0245

52894/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 413us/step - acc: 0.9920 - loss: 0.0245

52961/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 414us/step - acc: 0.9920 - loss: 0.0245

53018/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 414us/step - acc: 0.9920 - loss: 0.0245

53065/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9920 - loss: 0.0245

53119/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 415us/step - acc: 0.9920 - loss: 0.0245

53181/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 416us/step - acc: 0.9920 - loss: 0.0245

53232/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 416us/step - acc: 0.9920 - loss: 0.0245

53282/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 417us/step - acc: 0.9920 - loss: 0.0245

53348/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 417us/step - acc: 0.9920 - loss: 0.0245

53405/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 418us/step - acc: 0.9920 - loss: 0.0245

53463/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 418us/step - acc: 0.9920 - loss: 0.0245

53580/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 418us/step - acc: 0.9920 - loss: 0.0245

53686/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 418us/step - acc: 0.9920 - loss: 0.0245

53755/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 419us/step - acc: 0.9920 - loss: 0.0245

53832/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 419us/step - acc: 0.9920 - loss: 0.0245

53894/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 420us/step - acc: 0.9920 - loss: 0.0245

53974/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 420us/step - acc: 0.9920 - loss: 0.0245

54042/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 420us/step - acc: 0.9920 - loss: 0.0245

54109/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 421us/step - acc: 0.9919 - loss: 0.0245

54197/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 421us/step - acc: 0.9919 - loss: 0.0245

54284/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 421us/step - acc: 0.9919 - loss: 0.0245

54369/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 422us/step - acc: 0.9919 - loss: 0.0246

54455/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 422us/step - acc: 0.9919 - loss: 0.0246

54506/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 422us/step - acc: 0.9919 - loss: 0.0246

54559/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 423us/step - acc: 0.9919 - loss: 0.0246

54622/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 423us/step - acc: 0.9919 - loss: 0.0246

54681/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 424us/step - acc: 0.9919 - loss: 0.0246

54758/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 424us/step - acc: 0.9919 - loss: 0.0246

54856/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 424us/step - acc: 0.9919 - loss: 0.0246

54974/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 424us/step - acc: 0.9919 - loss: 0.0246

55080/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 424us/step - acc: 0.9919 - loss: 0.0246

55186/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 424us/step - acc: 0.9919 - loss: 0.0246

55296/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 424us/step - acc: 0.9919 - loss: 0.0246

55388/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9919 - loss: 0.0246

55481/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9919 - loss: 0.0246

55597/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9919 - loss: 0.0246

55713/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9919 - loss: 0.0246

55828/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9919 - loss: 0.0246

55943/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9919 - loss: 0.0246

56067/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9919 - loss: 0.0246

56188/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9919 - loss: 0.0246

56305/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9919 - loss: 0.0246

56413/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9919 - loss: 0.0246

56502/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9919 - loss: 0.0246

56614/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9919 - loss: 0.0246

56720/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9919 - loss: 0.0246

56839/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9919 - loss: 0.0246

56941/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9919 - loss: 0.0246

57057/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9919 - loss: 0.0246

57181/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9919 - loss: 0.0246

57283/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 426us/step - acc: 0.9919 - loss: 0.0246

57409/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9919 - loss: 0.0246

57528/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9919 - loss: 0.0246

57657/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 425us/step - acc: 0.9919 - loss: 0.0246

57775/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 425us/step - acc: 0.9919 - loss: 0.0246

57901/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 425us/step - acc: 0.9919 - loss: 0.0246

58019/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 425us/step - acc: 0.9919 - loss: 0.0246

58139/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 425us/step - acc: 0.9919 - loss: 0.0246

58255/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 425us/step - acc: 0.9919 - loss: 0.0246

58373/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 425us/step - acc: 0.9919 - loss: 0.0246

58485/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 425us/step - acc: 0.9919 - loss: 0.0246

58593/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 425us/step - acc: 0.9919 - loss: 0.0246

58699/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 426us/step - acc: 0.9919 - loss: 0.0246

58811/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 426us/step - acc: 0.9919 - loss: 0.0246

58877/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 426us/step - acc: 0.9919 - loss: 0.0246

58983/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 426us/step - acc: 0.9919 - loss: 0.0246

59094/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 426us/step - acc: 0.9919 - loss: 0.0246

59213/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 426us/step - acc: 0.9919 - loss: 0.0247

59335/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 426us/step - acc: 0.9919 - loss: 0.0247

59456/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 426us/step - acc: 0.9919 - loss: 0.0247

59576/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 426us/step - acc: 0.9919 - loss: 0.0247

59684/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 426us/step - acc: 0.9919 - loss: 0.0247

59799/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 426us/step - acc: 0.9919 - loss: 0.0247

59923/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 426us/step - acc: 0.9919 - loss: 0.0247

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 29s 485us/step - acc: 0.9919 - loss: 0.0247 - val_acc: 0.9696 - val_loss: 0.1289

Epoch 20/20

    1/60000 ━━━━━━━━━━━━━━━━━━━━ 13:19 13ms/step - acc: 1.0000 - loss: 1.1921e-07

  112/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 452us/step - acc: 0.9661 - loss: 0.0607     

  222/60000 ━━━━━━━━━━━━━━━━━━━━ 27s 454us/step - acc: 0.9798 - loss: 0.0393

  344/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 438us/step - acc: 0.9857 - loss: 0.0315

  453/60000 ━━━━━━━━━━━━━━━━━━━━ 26s 444us/step - acc: 0.9885 - loss: 0.0280

  578/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 435us/step - acc: 0.9900 - loss: 0.0269

  711/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 424us/step - acc: 0.9909 - loss: 0.0261

  834/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 422us/step - acc: 0.9913 - loss: 0.0255

  962/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 418us/step - acc: 0.9917 - loss: 0.0247

 1066/60000 ━━━━━━━━━━━━━━━━━━━━ 25s 424us/step - acc: 0.9916 - loss: 0.0246

 1194/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 421us/step - acc: 0.9917 - loss: 0.0243

 1327/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 416us/step - acc: 0.9917 - loss: 0.0240

 1461/60000 ━━━━━━━━━━━━━━━━━━━━ 24s 413us/step - acc: 0.9918 - loss: 0.0237

 1594/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 410us/step - acc: 0.9918 - loss: 0.0235

 1729/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 407us/step - acc: 0.9919 - loss: 0.0232

 1852/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 407us/step - acc: 0.9920 - loss: 0.0228

 1986/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 404us/step - acc: 0.9921 - loss: 0.0225

 2125/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 402us/step - acc: 0.9922 - loss: 0.0221

 2260/60000 ━━━━━━━━━━━━━━━━━━━━ 23s 400us/step - acc: 0.9924 - loss: 0.0217

 2396/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 398us/step - acc: 0.9925 - loss: 0.0214

 2531/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 397us/step - acc: 0.9926 - loss: 0.0211

 2666/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 395us/step - acc: 0.9927 - loss: 0.0208

 2805/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 394us/step - acc: 0.9928 - loss: 0.0205

 2938/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 393us/step - acc: 0.9929 - loss: 0.0203

 3074/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 392us/step - acc: 0.9930 - loss: 0.0201

 3207/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 391us/step - acc: 0.9930 - loss: 0.0199

 3330/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 392us/step - acc: 0.9931 - loss: 0.0198

 3468/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 391us/step - acc: 0.9931 - loss: 0.0196

 3596/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 391us/step - acc: 0.9932 - loss: 0.0195

 3734/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 390us/step - acc: 0.9932 - loss: 0.0194

 3870/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 389us/step - acc: 0.9933 - loss: 0.0192

 4007/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 388us/step - acc: 0.9933 - loss: 0.0191

 4144/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 388us/step - acc: 0.9934 - loss: 0.0190

 4278/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 387us/step - acc: 0.9934 - loss: 0.0188

 4412/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 387us/step - acc: 0.9935 - loss: 0.0187

 4539/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 387us/step - acc: 0.9935 - loss: 0.0186

 4661/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 388us/step - acc: 0.9936 - loss: 0.0185

 4786/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 388us/step - acc: 0.9936 - loss: 0.0184

 4850/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 393us/step - acc: 0.9936 - loss: 0.0184

 4931/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 397us/step - acc: 0.9937 - loss: 0.0183

 5027/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 399us/step - acc: 0.9937 - loss: 0.0182

 5125/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 402us/step - acc: 0.9937 - loss: 0.0181

 5230/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 403us/step - acc: 0.9938 - loss: 0.0181

 5341/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 404us/step - acc: 0.9938 - loss: 0.0180

 5465/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 404us/step - acc: 0.9938 - loss: 0.0179

 5581/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 405us/step - acc: 0.9938 - loss: 0.0178

 5685/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 406us/step - acc: 0.9939 - loss: 0.0178

 5782/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 408us/step - acc: 0.9939 - loss: 0.0177

 5891/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 409us/step - acc: 0.9939 - loss: 0.0177

 6005/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 410us/step - acc: 0.9939 - loss: 0.0176

 6124/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 410us/step - acc: 0.9939 - loss: 0.0176

 6243/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 410us/step - acc: 0.9939 - loss: 0.0176

 6360/60000 ━━━━━━━━━━━━━━━━━━━━ 22s 410us/step - acc: 0.9939 - loss: 0.0175

 6483/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 410us/step - acc: 0.9940 - loss: 0.0175

 6605/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 411us/step - acc: 0.9940 - loss: 0.0175

 6725/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 411us/step - acc: 0.9940 - loss: 0.0175

 6850/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 410us/step - acc: 0.9940 - loss: 0.0174

 6968/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 411us/step - acc: 0.9940 - loss: 0.0174

 7101/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 410us/step - acc: 0.9940 - loss: 0.0174

 7222/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 410us/step - acc: 0.9940 - loss: 0.0174

 7323/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 411us/step - acc: 0.9940 - loss: 0.0174

 7427/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 412us/step - acc: 0.9940 - loss: 0.0174

 7526/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 414us/step - acc: 0.9940 - loss: 0.0174

 7610/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 416us/step - acc: 0.9940 - loss: 0.0173

 7682/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 418us/step - acc: 0.9940 - loss: 0.0173

 7781/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 419us/step - acc: 0.9940 - loss: 0.0173

 7897/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 420us/step - acc: 0.9940 - loss: 0.0173

 8006/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 420us/step - acc: 0.9940 - loss: 0.0173

 8115/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 421us/step - acc: 0.9940 - loss: 0.0173

 8233/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 421us/step - acc: 0.9940 - loss: 0.0173

 8336/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 422us/step - acc: 0.9940 - loss: 0.0173

 8445/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 422us/step - acc: 0.9940 - loss: 0.0173

 8539/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 423us/step - acc: 0.9940 - loss: 0.0173

 8656/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 423us/step - acc: 0.9939 - loss: 0.0173

 8762/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 424us/step - acc: 0.9939 - loss: 0.0173

 8877/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 424us/step - acc: 0.9939 - loss: 0.0173

 8996/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 424us/step - acc: 0.9939 - loss: 0.0173

 9122/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 424us/step - acc: 0.9939 - loss: 0.0173

 9244/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 424us/step - acc: 0.9939 - loss: 0.0173

 9369/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 423us/step - acc: 0.9939 - loss: 0.0173

 9478/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 424us/step - acc: 0.9939 - loss: 0.0173

 9591/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 424us/step - acc: 0.9939 - loss: 0.0173

 9694/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 425us/step - acc: 0.9939 - loss: 0.0173

 9800/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 425us/step - acc: 0.9939 - loss: 0.0173

 9907/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 426us/step - acc: 0.9939 - loss: 0.0172

10013/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 426us/step - acc: 0.9939 - loss: 0.0172

10123/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 427us/step - acc: 0.9939 - loss: 0.0172

10234/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 427us/step - acc: 0.9939 - loss: 0.0172

10355/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 427us/step - acc: 0.9939 - loss: 0.0172

10474/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 427us/step - acc: 0.9939 - loss: 0.0172

10573/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 427us/step - acc: 0.9939 - loss: 0.0172

10671/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 428us/step - acc: 0.9939 - loss: 0.0172

10790/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 428us/step - acc: 0.9939 - loss: 0.0172

10917/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 428us/step - acc: 0.9939 - loss: 0.0172

11018/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 428us/step - acc: 0.9939 - loss: 0.0172

11106/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 429us/step - acc: 0.9939 - loss: 0.0172

11190/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 431us/step - acc: 0.9939 - loss: 0.0171

11259/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 433us/step - acc: 0.9939 - loss: 0.0171

11311/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 436us/step - acc: 0.9939 - loss: 0.0171

11391/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 437us/step - acc: 0.9939 - loss: 0.0171

11469/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 438us/step - acc: 0.9939 - loss: 0.0171

11569/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 439us/step - acc: 0.9939 - loss: 0.0171

11675/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 439us/step - acc: 0.9939 - loss: 0.0171

11788/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 439us/step - acc: 0.9939 - loss: 0.0171

11900/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 439us/step - acc: 0.9939 - loss: 0.0171

12016/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 439us/step - acc: 0.9939 - loss: 0.0171

12126/60000 ━━━━━━━━━━━━━━━━━━━━ 21s 439us/step - acc: 0.9939 - loss: 0.0171

12236/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 440us/step - acc: 0.9939 - loss: 0.0171

12365/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 439us/step - acc: 0.9939 - loss: 0.0170

12486/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 439us/step - acc: 0.9939 - loss: 0.0170

12600/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 439us/step - acc: 0.9939 - loss: 0.0170

12721/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 439us/step - acc: 0.9939 - loss: 0.0170

12849/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 438us/step - acc: 0.9940 - loss: 0.0170

12970/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 438us/step - acc: 0.9940 - loss: 0.0170

13094/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 438us/step - acc: 0.9940 - loss: 0.0170

13211/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 438us/step - acc: 0.9940 - loss: 0.0170

13321/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 438us/step - acc: 0.9940 - loss: 0.0169

13430/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 438us/step - acc: 0.9940 - loss: 0.0169

13496/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 440us/step - acc: 0.9940 - loss: 0.0169

13594/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 440us/step - acc: 0.9940 - loss: 0.0169

13700/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 440us/step - acc: 0.9940 - loss: 0.0169

13805/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 441us/step - acc: 0.9940 - loss: 0.0169

13916/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 441us/step - acc: 0.9940 - loss: 0.0169

14032/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 441us/step - acc: 0.9940 - loss: 0.0169

14134/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 441us/step - acc: 0.9940 - loss: 0.0169

14247/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 441us/step - acc: 0.9940 - loss: 0.0169

14359/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 441us/step - acc: 0.9940 - loss: 0.0169

14452/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 442us/step - acc: 0.9940 - loss: 0.0169

14572/60000 ━━━━━━━━━━━━━━━━━━━━ 20s 442us/step - acc: 0.9940 - loss: 0.0169

14702/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 441us/step - acc: 0.9940 - loss: 0.0169

14820/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 441us/step - acc: 0.9940 - loss: 0.0169

14948/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 441us/step - acc: 0.9940 - loss: 0.0169

15073/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 440us/step - acc: 0.9940 - loss: 0.0169

15194/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 440us/step - acc: 0.9940 - loss: 0.0169

15317/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 440us/step - acc: 0.9940 - loss: 0.0169

15437/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 440us/step - acc: 0.9940 - loss: 0.0169

15552/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 440us/step - acc: 0.9940 - loss: 0.0168

15648/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 440us/step - acc: 0.9940 - loss: 0.0168

15746/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 441us/step - acc: 0.9940 - loss: 0.0168

15856/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 441us/step - acc: 0.9940 - loss: 0.0168

15981/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 440us/step - acc: 0.9940 - loss: 0.0168

16086/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 441us/step - acc: 0.9940 - loss: 0.0168

16183/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 441us/step - acc: 0.9940 - loss: 0.0168

16291/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 441us/step - acc: 0.9940 - loss: 0.0168

16403/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 441us/step - acc: 0.9940 - loss: 0.0168

16522/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 441us/step - acc: 0.9940 - loss: 0.0168

16641/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 441us/step - acc: 0.9940 - loss: 0.0168

16763/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 441us/step - acc: 0.9940 - loss: 0.0168

16862/60000 ━━━━━━━━━━━━━━━━━━━━ 19s 441us/step - acc: 0.9940 - loss: 0.0168

16975/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 441us/step - acc: 0.9940 - loss: 0.0168

17084/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 441us/step - acc: 0.9940 - loss: 0.0168

17205/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 441us/step - acc: 0.9940 - loss: 0.0168

17331/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 441us/step - acc: 0.9940 - loss: 0.0168

17458/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 441us/step - acc: 0.9940 - loss: 0.0168

17590/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 440us/step - acc: 0.9940 - loss: 0.0168

17721/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 440us/step - acc: 0.9941 - loss: 0.0168

17856/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 439us/step - acc: 0.9941 - loss: 0.0168

17991/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 439us/step - acc: 0.9941 - loss: 0.0168

18126/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 438us/step - acc: 0.9941 - loss: 0.0168

18249/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 438us/step - acc: 0.9941 - loss: 0.0168

18376/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 438us/step - acc: 0.9941 - loss: 0.0168

18502/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 437us/step - acc: 0.9941 - loss: 0.0168

18639/60000 ━━━━━━━━━━━━━━━━━━━━ 18s 437us/step - acc: 0.9941 - loss: 0.0168

18775/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 436us/step - acc: 0.9941 - loss: 0.0168

18909/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 436us/step - acc: 0.9941 - loss: 0.0168

19045/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 435us/step - acc: 0.9941 - loss: 0.0168

19182/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 435us/step - acc: 0.9941 - loss: 0.0168

19319/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 434us/step - acc: 0.9941 - loss: 0.0168

19456/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 434us/step - acc: 0.9941 - loss: 0.0168

19594/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 434us/step - acc: 0.9941 - loss: 0.0168

19731/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 433us/step - acc: 0.9941 - loss: 0.0168

19863/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 433us/step - acc: 0.9941 - loss: 0.0168

20002/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 432us/step - acc: 0.9941 - loss: 0.0168

20142/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 432us/step - acc: 0.9941 - loss: 0.0168

20278/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 431us/step - acc: 0.9941 - loss: 0.0168

20416/60000 ━━━━━━━━━━━━━━━━━━━━ 17s 431us/step - acc: 0.9941 - loss: 0.0168

20551/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 430us/step - acc: 0.9941 - loss: 0.0168

20690/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 430us/step - acc: 0.9941 - loss: 0.0168

20817/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 430us/step - acc: 0.9941 - loss: 0.0168

20943/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 430us/step - acc: 0.9941 - loss: 0.0168

21080/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 429us/step - acc: 0.9941 - loss: 0.0168

21216/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 429us/step - acc: 0.9941 - loss: 0.0168

21353/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 428us/step - acc: 0.9941 - loss: 0.0168

21490/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 428us/step - acc: 0.9941 - loss: 0.0168

21623/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 428us/step - acc: 0.9941 - loss: 0.0168

21762/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 427us/step - acc: 0.9941 - loss: 0.0168

21895/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 427us/step - acc: 0.9941 - loss: 0.0168

22034/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 426us/step - acc: 0.9941 - loss: 0.0168

22172/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 426us/step - acc: 0.9941 - loss: 0.0169

22311/60000 ━━━━━━━━━━━━━━━━━━━━ 16s 426us/step - acc: 0.9941 - loss: 0.0169

22446/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 425us/step - acc: 0.9941 - loss: 0.0169

22585/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 425us/step - acc: 0.9941 - loss: 0.0169

22731/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 424us/step - acc: 0.9941 - loss: 0.0169

22870/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 424us/step - acc: 0.9941 - loss: 0.0169

23014/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 424us/step - acc: 0.9941 - loss: 0.0169

23144/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 423us/step - acc: 0.9941 - loss: 0.0169

23288/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 423us/step - acc: 0.9941 - loss: 0.0169

23421/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 423us/step - acc: 0.9941 - loss: 0.0169

23562/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 422us/step - acc: 0.9941 - loss: 0.0169

23693/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 422us/step - acc: 0.9941 - loss: 0.0169

23827/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 422us/step - acc: 0.9941 - loss: 0.0169

23946/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 422us/step - acc: 0.9941 - loss: 0.0169

24054/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 422us/step - acc: 0.9941 - loss: 0.0169

24140/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 423us/step - acc: 0.9941 - loss: 0.0169

24262/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 422us/step - acc: 0.9941 - loss: 0.0169

24385/60000 ━━━━━━━━━━━━━━━━━━━━ 15s 422us/step - acc: 0.9941 - loss: 0.0170

24506/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 422us/step - acc: 0.9941 - loss: 0.0170

24627/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 422us/step - acc: 0.9941 - loss: 0.0170

24738/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 422us/step - acc: 0.9941 - loss: 0.0170

24871/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 422us/step - acc: 0.9941 - loss: 0.0170

24971/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 423us/step - acc: 0.9941 - loss: 0.0170

25073/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 423us/step - acc: 0.9941 - loss: 0.0170

25199/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 423us/step - acc: 0.9941 - loss: 0.0170

25326/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 423us/step - acc: 0.9941 - loss: 0.0170

25461/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 422us/step - acc: 0.9941 - loss: 0.0170

25583/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 422us/step - acc: 0.9941 - loss: 0.0170

25722/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 422us/step - acc: 0.9941 - loss: 0.0170

25844/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 422us/step - acc: 0.9941 - loss: 0.0170

25979/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 422us/step - acc: 0.9941 - loss: 0.0170

26102/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 422us/step - acc: 0.9941 - loss: 0.0170

26234/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 421us/step - acc: 0.9941 - loss: 0.0170

26369/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 421us/step - acc: 0.9941 - loss: 0.0170

26507/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 421us/step - acc: 0.9941 - loss: 0.0171

26635/60000 ━━━━━━━━━━━━━━━━━━━━ 14s 421us/step - acc: 0.9941 - loss: 0.0171

26768/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 420us/step - acc: 0.9941 - loss: 0.0171

26843/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 421us/step - acc: 0.9941 - loss: 0.0171

26948/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 421us/step - acc: 0.9941 - loss: 0.0171

27058/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 421us/step - acc: 0.9940 - loss: 0.0171

27145/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 422us/step - acc: 0.9940 - loss: 0.0171

27272/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 422us/step - acc: 0.9940 - loss: 0.0171

27395/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 422us/step - acc: 0.9940 - loss: 0.0171

27525/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 422us/step - acc: 0.9940 - loss: 0.0171

27667/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 421us/step - acc: 0.9940 - loss: 0.0171

27797/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 421us/step - acc: 0.9940 - loss: 0.0171

27928/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 421us/step - acc: 0.9940 - loss: 0.0172

28067/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 421us/step - acc: 0.9940 - loss: 0.0172

28186/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 421us/step - acc: 0.9940 - loss: 0.0172

28297/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 421us/step - acc: 0.9940 - loss: 0.0172

28421/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 421us/step - acc: 0.9940 - loss: 0.0172

28528/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 421us/step - acc: 0.9940 - loss: 0.0172

28657/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 421us/step - acc: 0.9940 - loss: 0.0172

28770/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 421us/step - acc: 0.9940 - loss: 0.0172

28883/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 421us/step - acc: 0.9940 - loss: 0.0172

28978/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 421us/step - acc: 0.9940 - loss: 0.0172

29089/60000 ━━━━━━━━━━━━━━━━━━━━ 13s 421us/step - acc: 0.9940 - loss: 0.0173

29207/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 421us/step - acc: 0.9940 - loss: 0.0173

29312/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9940 - loss: 0.0173

29417/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9940 - loss: 0.0173

29541/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9940 - loss: 0.0173

29659/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9940 - loss: 0.0173

29757/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9940 - loss: 0.0173

29876/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9940 - loss: 0.0173

29978/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9940 - loss: 0.0173

30096/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9940 - loss: 0.0173

30203/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9940 - loss: 0.0173

30327/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9940 - loss: 0.0173

30448/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9940 - loss: 0.0174

30573/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9940 - loss: 0.0174

30696/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9940 - loss: 0.0174

30806/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9940 - loss: 0.0174

30915/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 423us/step - acc: 0.9940 - loss: 0.0174

31030/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 423us/step - acc: 0.9940 - loss: 0.0174

31155/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9940 - loss: 0.0174

31272/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 423us/step - acc: 0.9940 - loss: 0.0174

31397/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9940 - loss: 0.0174

31527/60000 ━━━━━━━━━━━━━━━━━━━━ 12s 422us/step - acc: 0.9940 - loss: 0.0174

31663/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 422us/step - acc: 0.9940 - loss: 0.0174

31785/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 422us/step - acc: 0.9940 - loss: 0.0175

31909/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 422us/step - acc: 0.9940 - loss: 0.0175

32037/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 422us/step - acc: 0.9940 - loss: 0.0175

32167/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 422us/step - acc: 0.9940 - loss: 0.0175

32290/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 422us/step - acc: 0.9940 - loss: 0.0175

32407/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 422us/step - acc: 0.9940 - loss: 0.0175

32530/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 422us/step - acc: 0.9940 - loss: 0.0175

32653/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 422us/step - acc: 0.9940 - loss: 0.0175

32768/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 422us/step - acc: 0.9940 - loss: 0.0175

32885/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 422us/step - acc: 0.9940 - loss: 0.0175

33003/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 422us/step - acc: 0.9940 - loss: 0.0175

33124/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 422us/step - acc: 0.9940 - loss: 0.0175

33252/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 421us/step - acc: 0.9940 - loss: 0.0176

33375/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 421us/step - acc: 0.9940 - loss: 0.0176

33496/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 421us/step - acc: 0.9939 - loss: 0.0176

33628/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 421us/step - acc: 0.9939 - loss: 0.0176

33756/60000 ━━━━━━━━━━━━━━━━━━━━ 11s 421us/step - acc: 0.9939 - loss: 0.0176

33881/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 421us/step - acc: 0.9939 - loss: 0.0176

34006/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 421us/step - acc: 0.9939 - loss: 0.0176

34146/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 421us/step - acc: 0.9939 - loss: 0.0176

34282/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 421us/step - acc: 0.9939 - loss: 0.0176

34408/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 420us/step - acc: 0.9939 - loss: 0.0176

34543/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 420us/step - acc: 0.9939 - loss: 0.0176

34673/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 420us/step - acc: 0.9939 - loss: 0.0176

34805/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 420us/step - acc: 0.9939 - loss: 0.0176

34942/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 420us/step - acc: 0.9939 - loss: 0.0177

35079/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 420us/step - acc: 0.9939 - loss: 0.0177

35217/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 419us/step - acc: 0.9939 - loss: 0.0177

35355/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 419us/step - acc: 0.9939 - loss: 0.0177

35492/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 419us/step - acc: 0.9939 - loss: 0.0177

35630/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 419us/step - acc: 0.9939 - loss: 0.0177

35766/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 419us/step - acc: 0.9939 - loss: 0.0177

35885/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 419us/step - acc: 0.9939 - loss: 0.0177

36015/60000 ━━━━━━━━━━━━━━━━━━━━ 10s 418us/step - acc: 0.9939 - loss: 0.0177

36152/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 418us/step - acc: 0.9939 - loss: 0.0177 

36273/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 418us/step - acc: 0.9939 - loss: 0.0177

36399/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 418us/step - acc: 0.9939 - loss: 0.0177

36523/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 418us/step - acc: 0.9939 - loss: 0.0177

36646/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 418us/step - acc: 0.9939 - loss: 0.0177

36761/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 418us/step - acc: 0.9939 - loss: 0.0178

36883/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 418us/step - acc: 0.9939 - loss: 0.0178

37002/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 418us/step - acc: 0.9939 - loss: 0.0178

37119/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 418us/step - acc: 0.9939 - loss: 0.0178

37240/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 418us/step - acc: 0.9939 - loss: 0.0178

37354/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 418us/step - acc: 0.9939 - loss: 0.0178

37462/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 418us/step - acc: 0.9939 - loss: 0.0178

37578/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 418us/step - acc: 0.9939 - loss: 0.0178

37689/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 418us/step - acc: 0.9939 - loss: 0.0178

37801/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 419us/step - acc: 0.9939 - loss: 0.0178

37922/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 419us/step - acc: 0.9939 - loss: 0.0178

38044/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 419us/step - acc: 0.9939 - loss: 0.0178

38172/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 418us/step - acc: 0.9939 - loss: 0.0178

38303/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 418us/step - acc: 0.9939 - loss: 0.0178

38432/60000 ━━━━━━━━━━━━━━━━━━━━ 9s 418us/step - acc: 0.9939 - loss: 0.0178

38554/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 418us/step - acc: 0.9939 - loss: 0.0179

38677/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 418us/step - acc: 0.9939 - loss: 0.0179

38801/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 418us/step - acc: 0.9939 - loss: 0.0179

38926/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 418us/step - acc: 0.9939 - loss: 0.0179

39038/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 418us/step - acc: 0.9939 - loss: 0.0179

39160/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 418us/step - acc: 0.9939 - loss: 0.0179

39270/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 418us/step - acc: 0.9939 - loss: 0.0179

39385/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 418us/step - acc: 0.9939 - loss: 0.0179

39513/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 418us/step - acc: 0.9939 - loss: 0.0179

39640/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 418us/step - acc: 0.9939 - loss: 0.0179

39771/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 418us/step - acc: 0.9939 - loss: 0.0179

39905/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 418us/step - acc: 0.9939 - loss: 0.0179

40041/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 418us/step - acc: 0.9939 - loss: 0.0179

40177/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 418us/step - acc: 0.9939 - loss: 0.0179

40314/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 417us/step - acc: 0.9939 - loss: 0.0179

40444/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 417us/step - acc: 0.9938 - loss: 0.0179

40570/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 417us/step - acc: 0.9938 - loss: 0.0180

40694/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 417us/step - acc: 0.9938 - loss: 0.0180

40816/60000 ━━━━━━━━━━━━━━━━━━━━ 8s 417us/step - acc: 0.9938 - loss: 0.0180

40927/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 417us/step - acc: 0.9938 - loss: 0.0180

41043/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 417us/step - acc: 0.9938 - loss: 0.0180

41161/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 417us/step - acc: 0.9938 - loss: 0.0180

41280/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 417us/step - acc: 0.9938 - loss: 0.0180

41398/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 417us/step - acc: 0.9938 - loss: 0.0180

41517/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 417us/step - acc: 0.9938 - loss: 0.0180

41640/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 417us/step - acc: 0.9938 - loss: 0.0180

41757/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 417us/step - acc: 0.9938 - loss: 0.0180

41895/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 417us/step - acc: 0.9938 - loss: 0.0180

42022/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 417us/step - acc: 0.9938 - loss: 0.0180

42150/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 417us/step - acc: 0.9938 - loss: 0.0180

42282/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 417us/step - acc: 0.9938 - loss: 0.0180

42412/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 417us/step - acc: 0.9938 - loss: 0.0180

42532/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 417us/step - acc: 0.9938 - loss: 0.0180

42662/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 417us/step - acc: 0.9938 - loss: 0.0180

42799/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 417us/step - acc: 0.9938 - loss: 0.0180

42937/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 416us/step - acc: 0.9938 - loss: 0.0180

43071/60000 ━━━━━━━━━━━━━━━━━━━━ 7s 416us/step - acc: 0.9938 - loss: 0.0181

43207/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 416us/step - acc: 0.9938 - loss: 0.0181

43340/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 416us/step - acc: 0.9938 - loss: 0.0181

43478/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 416us/step - acc: 0.9938 - loss: 0.0181

43618/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 416us/step - acc: 0.9938 - loss: 0.0181

43757/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 415us/step - acc: 0.9938 - loss: 0.0181

43896/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 415us/step - acc: 0.9938 - loss: 0.0181

44035/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 415us/step - acc: 0.9938 - loss: 0.0181

44176/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 415us/step - acc: 0.9938 - loss: 0.0181

44317/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 415us/step - acc: 0.9938 - loss: 0.0181

44457/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 415us/step - acc: 0.9938 - loss: 0.0181

44594/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 414us/step - acc: 0.9938 - loss: 0.0181

44735/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 414us/step - acc: 0.9938 - loss: 0.0181

44873/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 414us/step - acc: 0.9938 - loss: 0.0181

45011/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 414us/step - acc: 0.9938 - loss: 0.0181

45144/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 414us/step - acc: 0.9938 - loss: 0.0181

45272/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 414us/step - acc: 0.9938 - loss: 0.0181

45399/60000 ━━━━━━━━━━━━━━━━━━━━ 6s 414us/step - acc: 0.9938 - loss: 0.0181

45519/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 414us/step - acc: 0.9938 - loss: 0.0181

45637/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 414us/step - acc: 0.9938 - loss: 0.0181

45751/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 414us/step - acc: 0.9938 - loss: 0.0181

45861/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 414us/step - acc: 0.9938 - loss: 0.0181

45977/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 414us/step - acc: 0.9938 - loss: 0.0181

46105/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 414us/step - acc: 0.9938 - loss: 0.0182

46235/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 414us/step - acc: 0.9938 - loss: 0.0182

46356/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 414us/step - acc: 0.9938 - loss: 0.0182

46493/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 414us/step - acc: 0.9938 - loss: 0.0182

46628/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 414us/step - acc: 0.9938 - loss: 0.0182

46764/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 413us/step - acc: 0.9938 - loss: 0.0182

46896/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 413us/step - acc: 0.9938 - loss: 0.0182

47029/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 413us/step - acc: 0.9938 - loss: 0.0182

47166/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 413us/step - acc: 0.9938 - loss: 0.0182

47305/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 413us/step - acc: 0.9938 - loss: 0.0182

47443/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 413us/step - acc: 0.9938 - loss: 0.0182

47579/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 413us/step - acc: 0.9938 - loss: 0.0182

47717/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 413us/step - acc: 0.9938 - loss: 0.0182

47852/60000 ━━━━━━━━━━━━━━━━━━━━ 5s 412us/step - acc: 0.9938 - loss: 0.0182

47988/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 412us/step - acc: 0.9938 - loss: 0.0182

48128/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 412us/step - acc: 0.9938 - loss: 0.0182

48268/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 412us/step - acc: 0.9938 - loss: 0.0182

48409/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 412us/step - acc: 0.9938 - loss: 0.0182

48547/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 412us/step - acc: 0.9938 - loss: 0.0182

48683/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 412us/step - acc: 0.9938 - loss: 0.0182

48823/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 411us/step - acc: 0.9938 - loss: 0.0182

48962/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 411us/step - acc: 0.9938 - loss: 0.0183

49102/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 411us/step - acc: 0.9938 - loss: 0.0183

49239/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 411us/step - acc: 0.9938 - loss: 0.0183

49377/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 411us/step - acc: 0.9938 - loss: 0.0183

49514/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 411us/step - acc: 0.9938 - loss: 0.0183

49650/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 411us/step - acc: 0.9938 - loss: 0.0183

49788/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 411us/step - acc: 0.9938 - loss: 0.0183

49924/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 410us/step - acc: 0.9938 - loss: 0.0183

50062/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 410us/step - acc: 0.9938 - loss: 0.0183

50201/60000 ━━━━━━━━━━━━━━━━━━━━ 4s 410us/step - acc: 0.9937 - loss: 0.0183

50340/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 410us/step - acc: 0.9937 - loss: 0.0183

50479/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 410us/step - acc: 0.9937 - loss: 0.0183

50615/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 410us/step - acc: 0.9937 - loss: 0.0183

50752/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 410us/step - acc: 0.9937 - loss: 0.0183

50886/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 410us/step - acc: 0.9937 - loss: 0.0183

51025/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 409us/step - acc: 0.9937 - loss: 0.0183

51164/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 409us/step - acc: 0.9937 - loss: 0.0183

51290/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 409us/step - acc: 0.9937 - loss: 0.0183

51419/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 409us/step - acc: 0.9937 - loss: 0.0183

51545/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 409us/step - acc: 0.9937 - loss: 0.0183

51665/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 409us/step - acc: 0.9937 - loss: 0.0183

51789/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 409us/step - acc: 0.9937 - loss: 0.0184

51906/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 409us/step - acc: 0.9937 - loss: 0.0184

52027/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 409us/step - acc: 0.9937 - loss: 0.0184

52139/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 409us/step - acc: 0.9937 - loss: 0.0184

52254/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 409us/step - acc: 0.9937 - loss: 0.0184

52374/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 409us/step - acc: 0.9937 - loss: 0.0184

52495/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 409us/step - acc: 0.9937 - loss: 0.0184

52616/60000 ━━━━━━━━━━━━━━━━━━━━ 3s 409us/step - acc: 0.9937 - loss: 0.0184

52739/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 409us/step - acc: 0.9937 - loss: 0.0184

52861/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 409us/step - acc: 0.9937 - loss: 0.0184

52997/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 409us/step - acc: 0.9937 - loss: 0.0184

53132/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 409us/step - acc: 0.9937 - loss: 0.0184

53267/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 409us/step - acc: 0.9937 - loss: 0.0184

53404/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 409us/step - acc: 0.9937 - loss: 0.0184

53543/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 409us/step - acc: 0.9937 - loss: 0.0184

53680/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 409us/step - acc: 0.9937 - loss: 0.0184

53814/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 409us/step - acc: 0.9937 - loss: 0.0184

53939/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 409us/step - acc: 0.9937 - loss: 0.0184

54076/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 409us/step - acc: 0.9937 - loss: 0.0184

54214/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 408us/step - acc: 0.9937 - loss: 0.0184

54353/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 408us/step - acc: 0.9937 - loss: 0.0184

54487/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 408us/step - acc: 0.9937 - loss: 0.0184

54626/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 408us/step - acc: 0.9937 - loss: 0.0184

54764/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 408us/step - acc: 0.9937 - loss: 0.0185

54903/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 408us/step - acc: 0.9937 - loss: 0.0185

55041/60000 ━━━━━━━━━━━━━━━━━━━━ 2s 408us/step - acc: 0.9937 - loss: 0.0185

55177/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 408us/step - acc: 0.9937 - loss: 0.0185

55314/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 408us/step - acc: 0.9937 - loss: 0.0185

55452/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 407us/step - acc: 0.9937 - loss: 0.0185

55592/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 407us/step - acc: 0.9937 - loss: 0.0185

55729/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 407us/step - acc: 0.9937 - loss: 0.0185

55865/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 407us/step - acc: 0.9937 - loss: 0.0185

55992/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 407us/step - acc: 0.9937 - loss: 0.0185

56114/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 407us/step - acc: 0.9937 - loss: 0.0185

56251/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 407us/step - acc: 0.9937 - loss: 0.0185

56383/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 407us/step - acc: 0.9937 - loss: 0.0185

56513/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 407us/step - acc: 0.9937 - loss: 0.0185

56637/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 407us/step - acc: 0.9937 - loss: 0.0185

56770/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 407us/step - acc: 0.9937 - loss: 0.0185

56909/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 407us/step - acc: 0.9937 - loss: 0.0185

57044/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 407us/step - acc: 0.9937 - loss: 0.0185

57181/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 407us/step - acc: 0.9937 - loss: 0.0185

57317/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 406us/step - acc: 0.9937 - loss: 0.0185

57455/60000 ━━━━━━━━━━━━━━━━━━━━ 1s 406us/step - acc: 0.9937 - loss: 0.0185

57590/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 406us/step - acc: 0.9936 - loss: 0.0185

57728/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 406us/step - acc: 0.9936 - loss: 0.0185

57864/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 406us/step - acc: 0.9936 - loss: 0.0185

57998/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 406us/step - acc: 0.9936 - loss: 0.0185

58136/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 406us/step - acc: 0.9936 - loss: 0.0186

58274/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 406us/step - acc: 0.9936 - loss: 0.0186

58414/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 406us/step - acc: 0.9936 - loss: 0.0186

58551/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 406us/step - acc: 0.9936 - loss: 0.0186

58672/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 406us/step - acc: 0.9936 - loss: 0.0186

58804/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 406us/step - acc: 0.9936 - loss: 0.0186

58936/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 406us/step - acc: 0.9936 - loss: 0.0186

59066/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 405us/step - acc: 0.9936 - loss: 0.0186

59190/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 405us/step - acc: 0.9936 - loss: 0.0186

59318/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 405us/step - acc: 0.9936 - loss: 0.0186

59443/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 405us/step - acc: 0.9936 - loss: 0.0186

59572/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 405us/step - acc: 0.9936 - loss: 0.0186

59700/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 405us/step - acc: 0.9936 - loss: 0.0186

59830/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 405us/step - acc: 0.9936 - loss: 0.0186

59965/60000 ━━━━━━━━━━━━━━━━━━━━ 0s 405us/step - acc: 0.9936 - loss: 0.0186

60000/60000 ━━━━━━━━━━━━━━━━━━━━ 28s 464us/step - acc: 0.9936 - loss: 0.0186 - val_acc: 0.9688 - val_loss: 0.1185

TRAININGSDAUER: 575.09 Sek.

Wir sehen, dass das Training mit reinem SGD mit ca. 10 Minuten deutlich länger dauert als beim Batchtraining mit seinen 2 Sekunden - in beiden Fällen für 20 Epochen.

Das liegt daran, dass hier in jeder Epoche 60000 Mal sämtliche Gewichte angepasst werden, wohingegen vorher nur ein einziges Update pro Epoche stattfand.

Jetzt schauen wir uns die Performance an. Achten Sie auf den Wertebereich, der bei der Accuracy-Kurve zwischhen 0.9 und 1.0 liegt.

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(15,4))

set_subplot(ax[0], 'Loss', history2.history['loss'], 
            history2.history['val_loss'], [0, .5])
set_subplot(ax[1], 'Accuracy', history2.history['acc'], 
            history2.history['val_acc'], [0.9, 1])

plt.show()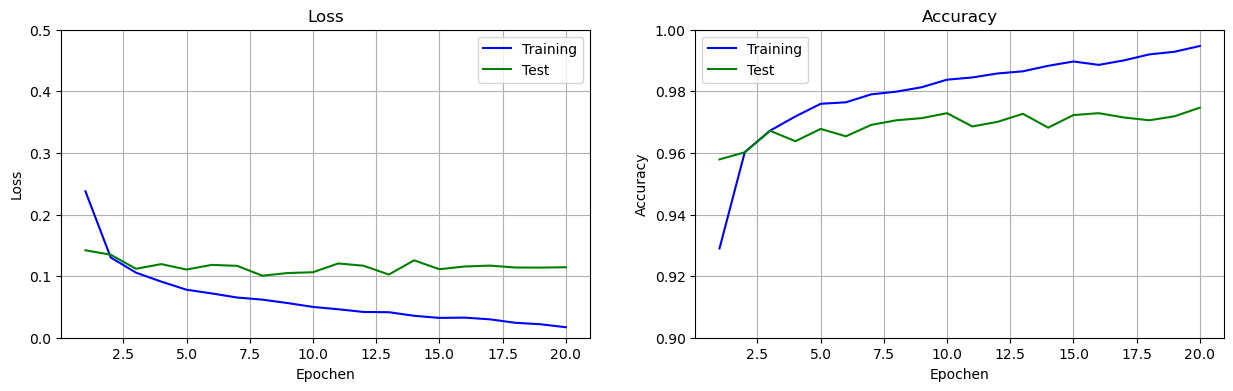

Wir sehen einen typischen Verlauf der Accuracy: Auf den Trainingsdaten steigt die Kurve immer weiter an, aber auf den Testdaten bleibt die Kurve in einem bestimmten Bereich. Sobald die Kurve auf den Testdaten sich einpendelt, kann man das Training beenden, weil das Training anschließend Overfitting betreibt.

Wir schauen uns jetzt noch einmal den finalen Accuracy-Wert auf den Testdaten an:

loss, acc = model.evaluate(x_test, y_test_1hot)
print(f"Evaluation auf den Testdaten:\n\nLoss = {loss:.3f}\nAccuracy = {acc:.3f}")

  1/313 ━━━━━━━━━━━━━━━━━━━━ 37s 119ms/step - acc: 0.9688 - loss: 0.0292

 71/313 ━━━━━━━━━━━━━━━━━━━━ 0s 715us/step - acc: 0.9675 - loss: 0.1172 

158/313 ━━━━━━━━━━━━━━━━━━━━ 0s 637us/step - acc: 0.9619 - loss: 0.1438

246/313 ━━━━━━━━━━━━━━━━━━━━ 0s 613us/step - acc: 0.9622 - loss: 0.1429

313/313 ━━━━━━━━━━━━━━━━━━━━ 0s 638us/step - acc: 0.9634 - loss: 0.1384

Evaluation auf den Testdaten:

Loss = 0.118
Accuracy = 0.969

Mit 97% Accuracy auf den Testdaten erreicht das mit reinem SGD trainierte Netz einen deutlich besseren Wert als das vorigen Netz, dass wir mit Batchtraining trainiert haben.

5.6.2 Minibatch (Batchgröße = 32)

Nachdem wir Batchtraining (alle Trainingsbeispiele pro Update) und reines SGD (Batchgröße = 1) ausprobiert haben, setzen wir jetzt die eigentliche Idee von Minibatch um, dass eine bestimmte Anzahl von (zufällig ausgewählten) Trainingsdaten durchlaufen wird, bevor dann ein Update durchgeführt wird. Es handelt sich also um einen Kompromiss zwischen Batchtraining und reinem SGD.

Im Keras ist bei der Methode SGD eine Batchgröße von 32 standardmäßig eingestellt. Diese probieren wir jetzt aus. Den Parameter batch_size lassen wir weg, damit die Standardgröße von 32 genommen wird. Alles andere bleibt wie in den beiden anderen Versuchen gleich.

model = Sequential()
model.add(Input(shape=(784,)))
model.add(Dense(60, 
                activation='sigmoid'))
model.add(Dense(10, activation='softmax'))

opt = SGD(learning_rate = 0.1)

model.compile(optimizer=opt,
              loss='categorical_crossentropy',
              metrics=['acc'])

start_time = time.time() 

history3 = model.fit(x_train, y_train_1hot, 
                     epochs=20,
                     verbose=1,
                     validation_data = (x_test, y_test_1hot))

duration = time.time() - start_time 
print(f'TRAININGSDAUER: {duration:.2f} Sek.')

Epoch 1/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 5:42 183ms/step - acc: 0.3125 - loss: 2.4901

  73/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 701us/step - acc: 0.3232 - loss: 2.1700  

 150/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 675us/step - acc: 0.4370 - loss: 1.9741

 234/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 648us/step - acc: 0.5073 - loss: 1.8116

 317/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 637us/step - acc: 0.5550 - loss: 1.6841

 400/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 632us/step - acc: 0.5900 - loss: 1.5805

 486/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 623us/step - acc: 0.6181 - loss: 1.4916

 573/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 616us/step - acc: 0.6408 - loss: 1.4163

 656/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 615us/step - acc: 0.6586 - loss: 1.3548

 687/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 664us/step - acc: 0.6645 - loss: 1.3339

 696/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 728us/step - acc: 0.6662 - loss: 1.3280

 764/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 729us/step - acc: 0.6779 - loss: 1.2860

 831/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 731us/step - acc: 0.6883 - loss: 1.2485

 887/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 742us/step - acc: 0.6961 - loss: 1.2198

 928/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 764us/step - acc: 0.7014 - loss: 1.2000

 982/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 773us/step - acc: 0.7079 - loss: 1.1756

1025/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 790us/step - acc: 0.7127 - loss: 1.1572

1078/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 798us/step - acc: 0.7183 - loss: 1.1359

1144/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 796us/step - acc: 0.7248 - loss: 1.1110

1206/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 797us/step - acc: 0.7304 - loss: 1.0892

1284/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 788us/step - acc: 0.7368 - loss: 1.0638

1338/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 793us/step - acc: 0.7409 - loss: 1.0474

1364/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 816us/step - acc: 0.7428 - loss: 1.0398

1411/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 824us/step - acc: 0.7461 - loss: 1.0265

1480/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 820us/step - acc: 0.7507 - loss: 1.0080

1547/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 818us/step - acc: 0.7549 - loss: 0.9912

1609/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 817us/step - acc: 0.7585 - loss: 0.9764

1679/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 813us/step - acc: 0.7624 - loss: 0.9605

1730/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 818us/step - acc: 0.7651 - loss: 0.9495

1808/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 811us/step - acc: 0.7690 - loss: 0.9335

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - acc: 0.7722 - loss: 0.9203 - val_acc: 0.9101 - val_loss: 0.3160

Epoch 2/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 23s 12ms/step - acc: 0.9688 - loss: 0.1811

  86/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 592us/step - acc: 0.9054 - loss: 0.3157

 161/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 630us/step - acc: 0.9057 - loss: 0.3214

 240/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 632us/step - acc: 0.9064 - loss: 0.3221

 319/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 633us/step - acc: 0.9068 - loss: 0.3229

 398/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 634us/step - acc: 0.9071 - loss: 0.3227

 482/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 627us/step - acc: 0.9075 - loss: 0.3219

 565/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 625us/step - acc: 0.9078 - loss: 0.3210

 641/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 631us/step - acc: 0.9081 - loss: 0.3201

 725/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 627us/step - acc: 0.9084 - loss: 0.3191

 811/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 623us/step - acc: 0.9087 - loss: 0.3183

 882/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 630us/step - acc: 0.9090 - loss: 0.3176

 964/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 628us/step - acc: 0.9092 - loss: 0.3167

1042/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 630us/step - acc: 0.9094 - loss: 0.3160

1120/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 631us/step - acc: 0.9096 - loss: 0.3154

1195/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 633us/step - acc: 0.9098 - loss: 0.3148

1261/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 641us/step - acc: 0.9099 - loss: 0.3142

1338/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 641us/step - acc: 0.9101 - loss: 0.3136

1413/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 643us/step - acc: 0.9103 - loss: 0.3131

1504/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 638us/step - acc: 0.9105 - loss: 0.3123

1595/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 633us/step - acc: 0.9108 - loss: 0.3116

1684/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 629us/step - acc: 0.9110 - loss: 0.3109

1767/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 628us/step - acc: 0.9112 - loss: 0.3103

1843/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 629us/step - acc: 0.9113 - loss: 0.3098

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 726us/step - acc: 0.9114 - loss: 0.3096 - val_acc: 0.9240 - val_loss: 0.2587

Epoch 3/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 20s 11ms/step - acc: 1.0000 - loss: 0.0591

  88/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 579us/step - acc: 0.9270 - loss: 0.2725

 167/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 607us/step - acc: 0.9262 - loss: 0.2665

 241/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 630us/step - acc: 0.9262 - loss: 0.2640

 328/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 616us/step - acc: 0.9258 - loss: 0.2633

 414/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 610us/step - acc: 0.9256 - loss: 0.2626

 489/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 619us/step - acc: 0.9253 - loss: 0.2625

 575/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 615us/step - acc: 0.9252 - loss: 0.2624

 660/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 612us/step - acc: 0.9251 - loss: 0.2624

 745/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 610us/step - acc: 0.9251 - loss: 0.2622

 816/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 619us/step - acc: 0.9251 - loss: 0.2620

 884/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 629us/step - acc: 0.9251 - loss: 0.2618

 937/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 647us/step - acc: 0.9251 - loss: 0.2616

 995/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 659us/step - acc: 0.9251 - loss: 0.2614

1068/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 661us/step - acc: 0.9251 - loss: 0.2610

1143/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 662us/step - acc: 0.9252 - loss: 0.2606

1217/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 663us/step - acc: 0.9252 - loss: 0.2603

1298/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 660us/step - acc: 0.9252 - loss: 0.2600

1377/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 659us/step - acc: 0.9252 - loss: 0.2597

1459/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 656us/step - acc: 0.9253 - loss: 0.2593

1542/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 654us/step - acc: 0.9253 - loss: 0.2590

1624/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 652us/step - acc: 0.9254 - loss: 0.2586

1707/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 650us/step - acc: 0.9254 - loss: 0.2583

1791/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 647us/step - acc: 0.9255 - loss: 0.2580

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 742us/step - acc: 0.9256 - loss: 0.2576 - val_acc: 0.9365 - val_loss: 0.2259

Epoch 4/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 19s 10ms/step - acc: 1.0000 - loss: 0.0727

  88/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 578us/step - acc: 0.9369 - loss: 0.2357

 167/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 607us/step - acc: 0.9344 - loss: 0.2387

 244/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 623us/step - acc: 0.9335 - loss: 0.2386

 327/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 619us/step - acc: 0.9331 - loss: 0.2372

 404/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 625us/step - acc: 0.9330 - loss: 0.2363

 486/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 624us/step - acc: 0.9329 - loss: 0.2354

 576/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 614us/step - acc: 0.9329 - loss: 0.2346

 665/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 608us/step - acc: 0.9330 - loss: 0.2340

 748/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 608us/step - acc: 0.9329 - loss: 0.2335

 830/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 608us/step - acc: 0.9329 - loss: 0.2331

 879/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 632us/step - acc: 0.9330 - loss: 0.2328

 962/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 629us/step - acc: 0.9331 - loss: 0.2323

1036/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 633us/step - acc: 0.9331 - loss: 0.2319

1116/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 633us/step - acc: 0.9333 - loss: 0.2314

1194/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 634us/step - acc: 0.9334 - loss: 0.2310

1277/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 632us/step - acc: 0.9335 - loss: 0.2305

1360/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 631us/step - acc: 0.9337 - loss: 0.2299

1441/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 630us/step - acc: 0.9338 - loss: 0.2295

1527/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 628us/step - acc: 0.9340 - loss: 0.2290

1611/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 626us/step - acc: 0.9341 - loss: 0.2286

1701/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 623us/step - acc: 0.9342 - loss: 0.2281

1786/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 621us/step - acc: 0.9343 - loss: 0.2277

1860/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 624us/step - acc: 0.9344 - loss: 0.2274

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 722us/step - acc: 0.9345 - loss: 0.2273 - val_acc: 0.9391 - val_loss: 0.2128

Epoch 5/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 20s 11ms/step - acc: 0.9375 - loss: 0.2328

  89/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 570us/step - acc: 0.9385 - loss: 0.2058

 182/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 555us/step - acc: 0.9386 - loss: 0.2057

 270/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 561us/step - acc: 0.9389 - loss: 0.2045

 357/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 564us/step - acc: 0.9392 - loss: 0.2035

 446/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 565us/step - acc: 0.9397 - loss: 0.2029

 535/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 565us/step - acc: 0.9401 - loss: 0.2026

 621/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 568us/step - acc: 0.9405 - loss: 0.2023

 710/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 568us/step - acc: 0.9408 - loss: 0.2022

 801/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 566us/step - acc: 0.9411 - loss: 0.2020

 885/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 570us/step - acc: 0.9413 - loss: 0.2018

 953/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 582us/step - acc: 0.9415 - loss: 0.2016

1038/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 583us/step - acc: 0.9417 - loss: 0.2015

1123/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 583us/step - acc: 0.9418 - loss: 0.2012

1210/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 583us/step - acc: 0.9420 - loss: 0.2010

1293/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 584us/step - acc: 0.9421 - loss: 0.2008

1367/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 590us/step - acc: 0.9422 - loss: 0.2006

1457/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 588us/step - acc: 0.9423 - loss: 0.2004

1544/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 587us/step - acc: 0.9424 - loss: 0.2003

1632/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 586us/step - acc: 0.9425 - loss: 0.2002

1720/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 585us/step - acc: 0.9425 - loss: 0.2001

1813/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 583us/step - acc: 0.9426 - loss: 0.2000

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 682us/step - acc: 0.9426 - loss: 0.1998 - val_acc: 0.9459 - val_loss: 0.1842

Epoch 6/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 17s 10ms/step - acc: 0.9688 - loss: 0.2947

  91/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 561us/step - acc: 0.9445 - loss: 0.1942

 185/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 548us/step - acc: 0.9442 - loss: 0.1973

 274/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 554us/step - acc: 0.9445 - loss: 0.1957

 370/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 546us/step - acc: 0.9452 - loss: 0.1939

 463/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 545us/step - acc: 0.9457 - loss: 0.1924

 556/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 544us/step - acc: 0.9462 - loss: 0.1906

 640/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 551us/step - acc: 0.9466 - loss: 0.1893

 731/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 551us/step - acc: 0.9471 - loss: 0.1879

 832/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 545us/step - acc: 0.9475 - loss: 0.1866

 932/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 540us/step - acc: 0.9477 - loss: 0.1857

1022/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 542us/step - acc: 0.9478 - loss: 0.1851

1109/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 545us/step - acc: 0.9479 - loss: 0.1846

1200/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 545us/step - acc: 0.9480 - loss: 0.1841

1294/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 545us/step - acc: 0.9481 - loss: 0.1837

1396/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 541us/step - acc: 0.9481 - loss: 0.1834

1496/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 538us/step - acc: 0.9482 - loss: 0.1831

1578/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 542us/step - acc: 0.9482 - loss: 0.1828

1673/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 541us/step - acc: 0.9483 - loss: 0.1825

1765/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 542us/step - acc: 0.9483 - loss: 0.1823

1857/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 542us/step - acc: 0.9484 - loss: 0.1820

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 633us/step - acc: 0.9484 - loss: 0.1820 - val_acc: 0.9513 - val_loss: 0.1696

Epoch 7/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 23s 13ms/step - acc: 0.9688 - loss: 0.0843

  91/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 557us/step - acc: 0.9503 - loss: 0.1575

 178/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 566us/step - acc: 0.9492 - loss: 0.1633

 274/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 552us/step - acc: 0.9493 - loss: 0.1670

 372/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 542us/step - acc: 0.9497 - loss: 0.1686

 442/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 569us/step - acc: 0.9498 - loss: 0.1693

 485/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 623us/step - acc: 0.9499 - loss: 0.1695

 572/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 616us/step - acc: 0.9500 - loss: 0.1697

 653/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 616us/step - acc: 0.9502 - loss: 0.1697

 715/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 633us/step - acc: 0.9502 - loss: 0.1695

 777/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 648us/step - acc: 0.9504 - loss: 0.1693

 832/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 665us/step - acc: 0.9504 - loss: 0.1691

 896/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 674us/step - acc: 0.9505 - loss: 0.1688

 974/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 671us/step - acc: 0.9507 - loss: 0.1685

1062/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 663us/step - acc: 0.9508 - loss: 0.1682

1149/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 656us/step - acc: 0.9509 - loss: 0.1678

1248/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 644us/step - acc: 0.9511 - loss: 0.1674

1345/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 635us/step - acc: 0.9512 - loss: 0.1671

1437/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 630us/step - acc: 0.9513 - loss: 0.1668

1538/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 621us/step - acc: 0.9515 - loss: 0.1665

1632/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 616us/step - acc: 0.9516 - loss: 0.1663

1741/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 606us/step - acc: 0.9517 - loss: 0.1660

1840/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 601us/step - acc: 0.9518 - loss: 0.1658

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 679us/step - acc: 0.9518 - loss: 0.1658 - val_acc: 0.9539 - val_loss: 0.1584

Epoch 8/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 24s 13ms/step - acc: 0.9688 - loss: 0.0964

 108/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 469us/step - acc: 0.9617 - loss: 0.1440

 213/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 474us/step - acc: 0.9583 - loss: 0.1511

 320/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 473us/step - acc: 0.9577 - loss: 0.1518

 423/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 476us/step - acc: 0.9573 - loss: 0.1524

 527/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 478us/step - acc: 0.9569 - loss: 0.1530

 636/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 475us/step - acc: 0.9567 - loss: 0.1532

 737/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 478us/step - acc: 0.9566 - loss: 0.1532

 812/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 496us/step - acc: 0.9565 - loss: 0.1531

 900/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 503us/step - acc: 0.9565 - loss: 0.1529

 997/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 505us/step - acc: 0.9565 - loss: 0.1528

1091/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 507us/step - acc: 0.9564 - loss: 0.1528

1187/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 508us/step - acc: 0.9564 - loss: 0.1527

1283/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 510us/step - acc: 0.9564 - loss: 0.1526

1384/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 509us/step - acc: 0.9564 - loss: 0.1525

1483/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 509us/step - acc: 0.9564 - loss: 0.1523

1579/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 510us/step - acc: 0.9564 - loss: 0.1521

1676/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 510us/step - acc: 0.9564 - loss: 0.1519

1775/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 510us/step - acc: 0.9564 - loss: 0.1518

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 587us/step - acc: 0.9564 - loss: 0.1517 - val_acc: 0.9563 - val_loss: 0.1485

Epoch 9/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 16s 9ms/step - acc: 0.9688 - loss: 0.1123

 108/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 467us/step - acc: 0.9598 - loss: 0.1407

 213/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 474us/step - acc: 0.9605 - loss: 0.1400

 291/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 521us/step - acc: 0.9606 - loss: 0.1393

 340/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 596us/step - acc: 0.9606 - loss: 0.1393

 425/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 595us/step - acc: 0.9605 - loss: 0.1395

 519/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 584us/step - acc: 0.9603 - loss: 0.1396

 620/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 570us/step - acc: 0.9601 - loss: 0.1396

 724/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 557us/step - acc: 0.9599 - loss: 0.1398

 833/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 545us/step - acc: 0.9597 - loss: 0.1403

 941/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 535us/step - acc: 0.9596 - loss: 0.1406

1051/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 527us/step - acc: 0.9596 - loss: 0.1407

1155/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 523us/step - acc: 0.9596 - loss: 0.1407

1249/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 524us/step - acc: 0.9597 - loss: 0.1407

1351/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 521us/step - acc: 0.9597 - loss: 0.1406

1457/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 518us/step - acc: 0.9598 - loss: 0.1405

1566/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 514us/step - acc: 0.9598 - loss: 0.1405

1674/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 511us/step - acc: 0.9598 - loss: 0.1404

1776/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 510us/step - acc: 0.9598 - loss: 0.1404

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 584us/step - acc: 0.9598 - loss: 0.1403 - val_acc: 0.9588 - val_loss: 0.1413

Epoch 10/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 16s 9ms/step - acc: 0.9688 - loss: 0.1366

 110/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 462us/step - acc: 0.9579 - loss: 0.1273

 215/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 471us/step - acc: 0.9587 - loss: 0.1293

 325/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 466us/step - acc: 0.9593 - loss: 0.1298

 434/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 465us/step - acc: 0.9597 - loss: 0.1303

 542/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 465us/step - acc: 0.9599 - loss: 0.1311

 653/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 462us/step - acc: 0.9601 - loss: 0.1315

 764/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 461us/step - acc: 0.9604 - loss: 0.1317

 864/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 466us/step - acc: 0.9605 - loss: 0.1319

 960/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 472us/step - acc: 0.9606 - loss: 0.1321

1068/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 471us/step - acc: 0.9607 - loss: 0.1323

1170/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 473us/step - acc: 0.9607 - loss: 0.1324

1271/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 475us/step - acc: 0.9608 - loss: 0.1325

1375/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 475us/step - acc: 0.9609 - loss: 0.1324

1484/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 474us/step - acc: 0.9610 - loss: 0.1324

1592/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 474us/step - acc: 0.9611 - loss: 0.1323

1702/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 472us/step - acc: 0.9612 - loss: 0.1321

1813/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 471us/step - acc: 0.9613 - loss: 0.1320

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 547us/step - acc: 0.9614 - loss: 0.1320 - val_acc: 0.9600 - val_loss: 0.1348

Epoch 11/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 17s 9ms/step - acc: 0.9375 - loss: 0.2580

  98/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 520us/step - acc: 0.9668 - loss: 0.1161

 180/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 564us/step - acc: 0.9665 - loss: 0.1176

 261/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 581us/step - acc: 0.9662 - loss: 0.1188

 348/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 581us/step - acc: 0.9660 - loss: 0.1194

 436/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 579us/step - acc: 0.9658 - loss: 0.1202

 520/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 581us/step - acc: 0.9657 - loss: 0.1210

 603/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 585us/step - acc: 0.9655 - loss: 0.1216

 690/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 584us/step - acc: 0.9654 - loss: 0.1220

 776/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 584us/step - acc: 0.9653 - loss: 0.1222

 861/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 585us/step - acc: 0.9653 - loss: 0.1224

 951/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 582us/step - acc: 0.9652 - loss: 0.1224

1032/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 585us/step - acc: 0.9652 - loss: 0.1224

1117/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 586us/step - acc: 0.9652 - loss: 0.1223

1205/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 585us/step - acc: 0.9652 - loss: 0.1221

1289/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 586us/step - acc: 0.9653 - loss: 0.1220

1372/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 587us/step - acc: 0.9653 - loss: 0.1219

1459/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 586us/step - acc: 0.9653 - loss: 0.1219

1543/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 587us/step - acc: 0.9653 - loss: 0.1218

1626/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 588us/step - acc: 0.9653 - loss: 0.1218

1720/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 585us/step - acc: 0.9653 - loss: 0.1217

1801/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 587us/step - acc: 0.9653 - loss: 0.1218

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 683us/step - acc: 0.9653 - loss: 0.1218 - val_acc: 0.9620 - val_loss: 0.1277

Epoch 12/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 22s 12ms/step - acc: 0.9688 - loss: 0.1040

  82/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 622us/step - acc: 0.9690 - loss: 0.1211

 172/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 588us/step - acc: 0.9694 - loss: 0.1175

 260/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 591us/step - acc: 0.9695 - loss: 0.1172

 346/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 590us/step - acc: 0.9694 - loss: 0.1175

 426/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 597us/step - acc: 0.9695 - loss: 0.1170

 508/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 600us/step - acc: 0.9694 - loss: 0.1167

 594/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 598us/step - acc: 0.9694 - loss: 0.1165

 681/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 597us/step - acc: 0.9694 - loss: 0.1163

 765/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 598us/step - acc: 0.9693 - loss: 0.1163

 856/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 593us/step - acc: 0.9691 - loss: 0.1163

 939/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 594us/step - acc: 0.9689 - loss: 0.1165

1011/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 602us/step - acc: 0.9688 - loss: 0.1166

1085/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 607us/step - acc: 0.9687 - loss: 0.1166

1152/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 615us/step - acc: 0.9686 - loss: 0.1167

1237/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 613us/step - acc: 0.9686 - loss: 0.1167

1326/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 610us/step - acc: 0.9685 - loss: 0.1167

1413/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 608us/step - acc: 0.9684 - loss: 0.1168

1498/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 607us/step - acc: 0.9684 - loss: 0.1169

1590/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 604us/step - acc: 0.9683 - loss: 0.1169

1678/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 602us/step - acc: 0.9683 - loss: 0.1169

1769/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 599us/step - acc: 0.9682 - loss: 0.1169

1864/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 596us/step - acc: 0.9682 - loss: 0.1169

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 681us/step - acc: 0.9682 - loss: 0.1169 - val_acc: 0.9629 - val_loss: 0.1252

Epoch 13/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 19s 10ms/step - acc: 0.9062 - loss: 0.3200

  93/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 545us/step - acc: 0.9720 - loss: 0.1054

 187/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 540us/step - acc: 0.9709 - loss: 0.1076

 279/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 542us/step - acc: 0.9707 - loss: 0.1078

 372/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 541us/step - acc: 0.9705 - loss: 0.1081

 468/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 537us/step - acc: 0.9703 - loss: 0.1083

 556/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 543us/step - acc: 0.9703 - loss: 0.1082

 654/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 538us/step - acc: 0.9702 - loss: 0.1081

 752/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 535us/step - acc: 0.9702 - loss: 0.1083

 833/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 543us/step - acc: 0.9701 - loss: 0.1083

 918/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 548us/step - acc: 0.9701 - loss: 0.1083

1005/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 551us/step - acc: 0.9701 - loss: 0.1082

1094/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 552us/step - acc: 0.9701 - loss: 0.1082

1177/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 556us/step - acc: 0.9701 - loss: 0.1082

1266/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 557us/step - acc: 0.9701 - loss: 0.1082

1360/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 555us/step - acc: 0.9701 - loss: 0.1083

1443/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 558us/step - acc: 0.9701 - loss: 0.1083

1535/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 557us/step - acc: 0.9701 - loss: 0.1083

1632/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 555us/step - acc: 0.9701 - loss: 0.1083

1730/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 552us/step - acc: 0.9701 - loss: 0.1083

1815/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 554us/step - acc: 0.9700 - loss: 0.1083

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 650us/step - acc: 0.9700 - loss: 0.1083 - val_acc: 0.9633 - val_loss: 0.1231

Epoch 14/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 18s 10ms/step - acc: 1.0000 - loss: 0.0707

  91/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 560us/step - acc: 0.9773 - loss: 0.0943

 199/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 508us/step - acc: 0.9734 - loss: 0.0985

 301/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 503us/step - acc: 0.9725 - loss: 0.0998

 405/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 498us/step - acc: 0.9720 - loss: 0.1005

 514/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 490us/step - acc: 0.9717 - loss: 0.1010

 608/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 497us/step - acc: 0.9716 - loss: 0.1014

 672/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 525us/step - acc: 0.9715 - loss: 0.1016

 761/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 530us/step - acc: 0.9714 - loss: 0.1018

 856/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 530us/step - acc: 0.9714 - loss: 0.1018

 957/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 526us/step - acc: 0.9714 - loss: 0.1019

1064/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 520us/step - acc: 0.9714 - loss: 0.1018

1165/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 518us/step - acc: 0.9714 - loss: 0.1017

1274/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 513us/step - acc: 0.9715 - loss: 0.1017

1379/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 511us/step - acc: 0.9715 - loss: 0.1018

1489/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 507us/step - acc: 0.9715 - loss: 0.1018

1596/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 504us/step - acc: 0.9715 - loss: 0.1019

1706/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 501us/step - acc: 0.9715 - loss: 0.1019

1811/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 500us/step - acc: 0.9715 - loss: 0.1020

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 585us/step - acc: 0.9714 - loss: 0.1021 - val_acc: 0.9641 - val_loss: 0.1198

Epoch 15/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 16s 9ms/step - acc: 1.0000 - loss: 0.0605

  57/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 896us/step - acc: 0.9708 - loss: 0.1037

 137/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 737us/step - acc: 0.9711 - loss: 0.1030

 245/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 617us/step - acc: 0.9718 - loss: 0.1025

 348/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 579us/step - acc: 0.9724 - loss: 0.1020

 457/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 551us/step - acc: 0.9724 - loss: 0.1020

 567/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 533us/step - acc: 0.9724 - loss: 0.1019

 677/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 520us/step - acc: 0.9724 - loss: 0.1019

 785/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 513us/step - acc: 0.9724 - loss: 0.1018

 888/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 510us/step - acc: 0.9724 - loss: 0.1018

 986/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 510us/step - acc: 0.9724 - loss: 0.1017

1092/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 506us/step - acc: 0.9725 - loss: 0.1016

1198/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 503us/step - acc: 0.9726 - loss: 0.1013

1300/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 504us/step - acc: 0.9726 - loss: 0.1011

1386/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 509us/step - acc: 0.9726 - loss: 0.1009

1471/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 513us/step - acc: 0.9727 - loss: 0.1007

1572/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 514us/step - acc: 0.9727 - loss: 0.1004

1660/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 517us/step - acc: 0.9727 - loss: 0.1003

1755/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 518us/step - acc: 0.9727 - loss: 0.1002

1857/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 517us/step - acc: 0.9727 - loss: 0.1001

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 594us/step - acc: 0.9727 - loss: 0.1001 - val_acc: 0.9662 - val_loss: 0.1142

Epoch 16/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 16s 9ms/step - acc: 0.9688 - loss: 0.0966

 102/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 498us/step - acc: 0.9776 - loss: 0.0911

 211/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 479us/step - acc: 0.9762 - loss: 0.0906

 322/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 470us/step - acc: 0.9757 - loss: 0.0902

 432/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 467us/step - acc: 0.9752 - loss: 0.0906

 533/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 490us/step - acc: 0.9750 - loss: 0.0910

 589/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 531us/step - acc: 0.9748 - loss: 0.0911

 673/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 539us/step - acc: 0.9747 - loss: 0.0913

 743/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 556us/step - acc: 0.9746 - loss: 0.0914

 831/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 559us/step - acc: 0.9746 - loss: 0.0915

 928/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 555us/step - acc: 0.9746 - loss: 0.0917

1020/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 554us/step - acc: 0.9745 - loss: 0.0920

1114/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 553us/step - acc: 0.9744 - loss: 0.0922

1208/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 551us/step - acc: 0.9743 - loss: 0.0924

1289/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 556us/step - acc: 0.9743 - loss: 0.0925

1350/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 568us/step - acc: 0.9743 - loss: 0.0926

1438/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 568us/step - acc: 0.9742 - loss: 0.0927

1525/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 569us/step - acc: 0.9742 - loss: 0.0928

1622/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 566us/step - acc: 0.9742 - loss: 0.0930

1693/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 572us/step - acc: 0.9741 - loss: 0.0930

1771/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 575us/step - acc: 0.9741 - loss: 0.0931

1846/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 579us/step - acc: 0.9741 - loss: 0.0932

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 724us/step - acc: 0.9741 - loss: 0.0932 - val_acc: 0.9663 - val_loss: 0.1127

Epoch 17/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 18s 10ms/step - acc: 1.0000 - loss: 0.0524

  67/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 774us/step - acc: 0.9712 - loss: 0.1065

 155/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 657us/step - acc: 0.9725 - loss: 0.1003

 253/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 601us/step - acc: 0.9736 - loss: 0.0960

 357/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 567us/step - acc: 0.9746 - loss: 0.0932

 467/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 541us/step - acc: 0.9752 - loss: 0.0913

 578/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 524us/step - acc: 0.9755 - loss: 0.0904

 680/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 519us/step - acc: 0.9757 - loss: 0.0900

 760/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 530us/step - acc: 0.9757 - loss: 0.0898

 850/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 533us/step - acc: 0.9758 - loss: 0.0896

 947/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 531us/step - acc: 0.9758 - loss: 0.0894

1051/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 527us/step - acc: 0.9758 - loss: 0.0893

1155/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 523us/step - acc: 0.9758 - loss: 0.0892

1263/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 517us/step - acc: 0.9757 - loss: 0.0893

1365/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 516us/step - acc: 0.9757 - loss: 0.0893

1461/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 516us/step - acc: 0.9756 - loss: 0.0893

1568/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 513us/step - acc: 0.9756 - loss: 0.0894

1660/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 515us/step - acc: 0.9755 - loss: 0.0895

1755/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 516us/step - acc: 0.9754 - loss: 0.0895

1862/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 513us/step - acc: 0.9754 - loss: 0.0896

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 598us/step - acc: 0.9754 - loss: 0.0896 - val_acc: 0.9676 - val_loss: 0.1087

Epoch 18/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 18s 10ms/step - acc: 1.0000 - loss: 0.0405

 104/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 489us/step - acc: 0.9795 - loss: 0.0796

 211/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 479us/step - acc: 0.9788 - loss: 0.0804

 317/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 478us/step - acc: 0.9782 - loss: 0.0815

 414/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 487us/step - acc: 0.9778 - loss: 0.0826

 518/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 487us/step - acc: 0.9775 - loss: 0.0837

 623/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 486us/step - acc: 0.9772 - loss: 0.0845

 727/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 485us/step - acc: 0.9770 - loss: 0.0851

 834/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 483us/step - acc: 0.9769 - loss: 0.0854

 932/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 486us/step - acc: 0.9768 - loss: 0.0855

1034/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 487us/step - acc: 0.9768 - loss: 0.0855

1137/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 487us/step - acc: 0.9768 - loss: 0.0855

1236/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 489us/step - acc: 0.9768 - loss: 0.0855

1340/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 488us/step - acc: 0.9768 - loss: 0.0855

1446/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 487us/step - acc: 0.9768 - loss: 0.0856

1549/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 487us/step - acc: 0.9767 - loss: 0.0858

1653/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 487us/step - acc: 0.9767 - loss: 0.0859

1756/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 487us/step - acc: 0.9767 - loss: 0.0860

1861/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 486us/step - acc: 0.9766 - loss: 0.0861

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 564us/step - acc: 0.9766 - loss: 0.0861 - val_acc: 0.9686 - val_loss: 0.1060

Epoch 19/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 20s 11ms/step - acc: 0.9688 - loss: 0.2103

 109/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 464us/step - acc: 0.9730 - loss: 0.1104

 219/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 460us/step - acc: 0.9744 - loss: 0.1014

 312/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 484us/step - acc: 0.9750 - loss: 0.0984

 414/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 486us/step - acc: 0.9755 - loss: 0.0958

 515/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 488us/step - acc: 0.9757 - loss: 0.0942

 611/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 494us/step - acc: 0.9759 - loss: 0.0929

 711/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 496us/step - acc: 0.9762 - loss: 0.0915

 807/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 499us/step - acc: 0.9764 - loss: 0.0904

 907/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 499us/step - acc: 0.9765 - loss: 0.0896

1001/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 502us/step - acc: 0.9766 - loss: 0.0890

1099/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 503us/step - acc: 0.9766 - loss: 0.0886

1193/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 505us/step - acc: 0.9766 - loss: 0.0883

1299/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 503us/step - acc: 0.9767 - loss: 0.0879

1405/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 501us/step - acc: 0.9767 - loss: 0.0875

1511/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 499us/step - acc: 0.9768 - loss: 0.0872

1612/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 499us/step - acc: 0.9768 - loss: 0.0870

1723/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 496us/step - acc: 0.9769 - loss: 0.0867

1833/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 494us/step - acc: 0.9769 - loss: 0.0865

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 569us/step - acc: 0.9769 - loss: 0.0864 - val_acc: 0.9684 - val_loss: 0.1040

Epoch 20/20

   1/1875 ━━━━━━━━━━━━━━━━━━━━ 18s 10ms/step - acc: 1.0000 - loss: 0.0234

  98/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 517us/step - acc: 0.9822 - loss: 0.0699

 196/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 516us/step - acc: 0.9820 - loss: 0.0708

 304/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 498us/step - acc: 0.9815 - loss: 0.0724

 413/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 489us/step - acc: 0.9814 - loss: 0.0728

 523/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 482us/step - acc: 0.9812 - loss: 0.0733

 630/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 480us/step - acc: 0.9809 - loss: 0.0739

 739/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 477us/step - acc: 0.9807 - loss: 0.0744

 847/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 476us/step - acc: 0.9806 - loss: 0.0747

 950/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 477us/step - acc: 0.9805 - loss: 0.0749

1056/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 477us/step - acc: 0.9804 - loss: 0.0751

1159/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 478us/step - acc: 0.9803 - loss: 0.0753

1265/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 477us/step - acc: 0.9801 - loss: 0.0756

1371/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 477us/step - acc: 0.9800 - loss: 0.0759

1474/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 478us/step - acc: 0.9799 - loss: 0.0761

1579/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 478us/step - acc: 0.9798 - loss: 0.0764

1687/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 477us/step - acc: 0.9797 - loss: 0.0766

1783/1875 ━━━━━━━━━━━━━━━━━━━━ 0s 480us/step - acc: 0.9796 - loss: 0.0768

1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 566us/step - acc: 0.9796 - loss: 0.0770 - val_acc: 0.9688 - val_loss: 0.1030

TRAININGSDAUER: 26.25 Sek.

Minibatch liegt mit einer Dauer von ca. 22 Sekunden zwischen Batch-Training (3 Sek.) und reinem SGD (8 Min.). Interessant ist, dass es doch erheblich schneller ist als reines SGD.

Wir sehen uns wieder die Performance an:

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(15,4))

set_subplot(ax[0], 'Loss', history3.history['loss'], 
            history3.history['val_loss'], [0, 1])
set_subplot(ax[1], 'Accuracy', history3.history['acc'], 
            history3.history['val_acc'], [0.8, 1])

plt.show()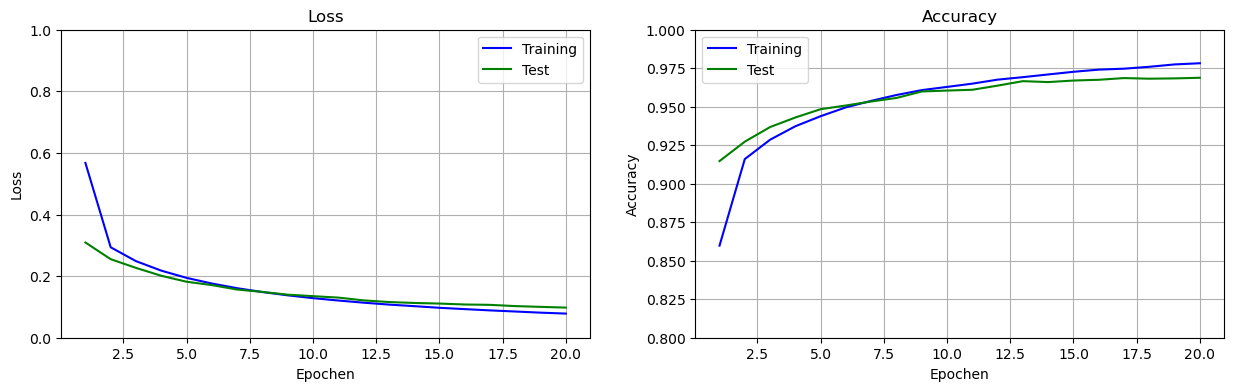

loss, acc = model.evaluate(x_test, y_test_1hot)
print(f"Evaluation auf den Testdaten:\n\nLoss = {loss:.3f}\nAccuracy = {acc:.3f}")

  1/313 ━━━━━━━━━━━━━━━━━━━━ 2s 9ms/step - acc: 0.9688 - loss: 0.1652

119/313 ━━━━━━━━━━━━━━━━━━━━ 0s 424us/step - acc: 0.9640 - loss: 0.1184

241/313 ━━━━━━━━━━━━━━━━━━━━ 0s 417us/step - acc: 0.9620 - loss: 0.1230

313/313 ━━━━━━━━━━━━━━━━━━━━ 0s 439us/step - acc: 0.9634 - loss: 0.1188

Evaluation auf den Testdaten:

Loss = 0.103
Accuracy = 0.969

Die Performance für unser Minibatch-Training mit Batchgröße 32 ist mit einer 97% Accuracy auf den Testdaten praktisch gleich zur Performance mit reinem SGD.

5.6.3 Fazit

Schauen wir uns die Resultate nochmal im Vergleich an (unten sieht man auch die jeweilige Accuracy als Kurve über die Epochen).

	Trainingsdauer	Accuracy (Test)
Batchtraining	3 Sek	27%
Reines SGD	10 Min	97%
Minibatch (32)	22 Sek	97%

Es scheint - zumindest bei diesen Daten - so zu sein, dass man mit Minibatch-Training mit der voreingestellten Batchgröße am besten fährt, da man eine hohe Accuracy bei tolerierbarer Trainingsdauer erzielt.

Wir sehen uns nochmal die Kurven der drei Ansätze nebeneinander an.

fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(15,4))

set_subplot(ax[0], 'Batchgröße 60000 / Accuracy', history1.history['acc'], history1.history['val_acc'], [0, 1])
set_subplot(ax[1], 'Batchgröße 1 / Accuracy', history2.history['acc'], history2.history['val_acc'], [0.85, 1])
set_subplot(ax[2], 'Batchgröße 32 / Accuracy', history3.history['acc'], history3.history['val_acc'], [0.85, 1])

plt.show()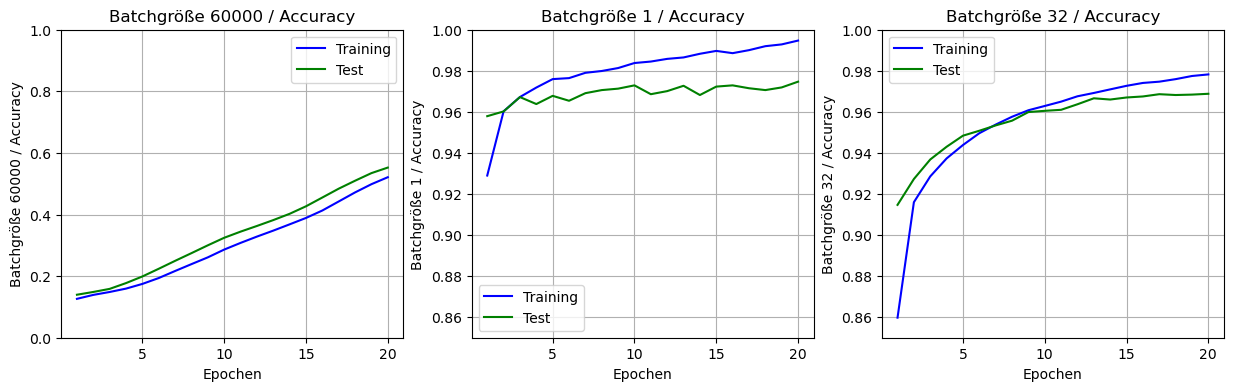

Wichtig ist immer, sich die Rahmenbedingungen des obigen “Experiments” vor Augen zu führen. Wir haben die Optimierungsmethode Stochastic Gradient Descent mit einer Lernrate von 0.1 verwendet und für 20 Epochen trainiert. Wir hatten ein FNN mit einer versteckten Schicht mit 60 Neuronen und haben auf den MNIST-Daten gearbeitet. Sollte sich einer dieser Umstände ändern, kann das die Ergebnisse verändern.

Zudem müsste man jede der drei Variante mehrfach testen (z.B. 10x) und dann den Mittelwert von Dauer und Accuracy nehmen, um statistische Glaubwürdigkeit zu erreichen. In unserem Beispiel sind die Unterschiede allerdings so deutlich, dass wir uns das ersparen.

Chollet, François. 2021. Deep Learning with Python, 2nd Edition. 2nd ed. Manning.