import numpy as np
import matplotlib.pyplot as plt3 Perzeptron
Wir lernen die grundlegenden Konzepte Neuronaler Netze für Klassifikationsprobleme anhand des Perzeptrons kennen. Dabei beschränken wir uns auf binäre Klassifikation. Wir sehen uns die Berechnung des Outputs an und insbesondere den Lernschritt und das Lernverfahren. Den Lernalgorithmus leiten wir mit Hilfe von Gradientenabstieg her. Wir nehmen eine eigene Implementierung in Python vor, um die Verarbeitung der Daten und die Umsetzung des Lernverfahrens zu verstehen. Dabei lernen wir auch den Sinn von Feature-Scaling kennen und den Unterschied zwischen Stochastic Gradient Descent und Minibatch.
Künstliche Neuronen, Perzeptron, Rohinput, Aktivierung, Schwellwert, Bias-Neuron, Verlustfunktion/Fehlerfunktion, Perzeptron-Lernalgorithmus, Feature-Scaling (Standardisieren, Normalisieren), Stochastic Gradient Descent, Minibatch
Nach Abschluss des Kapitels können Sie
- Unterschiede und Gemeinsamkeiten zwischen biologischen und künstlichen neuronalen Netzen beschreiben.
- das Perzeptron mathematisch erklären.
- die Implementierung logischer Operatoren wie AND und OR mit einem Perzeptron formulieren und begründen.
- den Lernalgorithmus aus dem Gradientenabstieg herleiten sowie Konzepte wie Zielfunktion und Fehlerlandschaft erklären.
- eine Python-Implementierung des Perzeptrons analysieren und deren Funktionsweise erläutern.
- die Feature-Scaling-Techniken Normalisierung und Standardisierung definieren, unterscheiden und anwenden.
- die Trainingsmethoden Stochastic Gradient Descent (SGD) und Minibatch Training erklären und deren Unterschiede benennen.
Datensatz
Iris-Datensatz: Abschnitt 3.4.1
Importe
3.1 Klassifikation mit künstlichen Neuronen
Nachdem wir gesehen haben, wie wir mit Regression einen Wert vorhersagen können, kommen wir jetzt zur Frage, wie man eine Klasse, Kategorie oder Label vorhersagt. Genauer gesagt: Wir suchen zu einem Feature-Vektor die dazugehörige Klasse oder Kategorie. Ein klassisches Beispiel ist die Klassifikation von e-Mails in eine der zwei Klassen SPAM oder nicht-SPAM. Bei zwei möglichen Klassen spricht man von binärer Klassifikation.
Wir nutzen das Szenario der binären Klassifikation, um unser erstes künstliche Neuronales Netz einzuführen, das Perzeptron.
Formal haben einen Datensatz von \(N\) gelabelten Beispielen \((x^{k}, y^{k})\) mit \(k = 1, \ldots, N\). Das \(x^k \in \mathbb{R}^n\) ist ein \(n\)-dimensionaler Feature-Vektor. Im Fall der binären Klassifikation ist der Ausgabewert \(y \in \{0, 1\}\) ein binärer Wert, z.B. SPAM (= 1) oder nicht-SPAM (= 0).
Zwei klassische Beispiele sind
- Klassfikation von Bildern: der Feature-Vektor \(x\) enthält alle Pixelwerte eines Bildes in Form eines Arrays und Kategorie \(y\) gibt z.B. an, ob es sich um das Bild einer Katze handelt (\(y=1\)) oder nicht (\(y=0\)).
- Klassfikation von e-Mails: der Feature-Vektor \(x\) repräsentiert die “Eigenschaften” einer e-Mail. Man nehme etwa 2000 ausgewählte, alphabetisch sortierte Wörter, die also einen eindeutigen Wortindex haben. Vektor \(x \in \mathbb{R}^{2000}\) hat für jedes Wort, das in der entsprechenden Mail enthalten ist, an dem entsprechenden Wortindex eine 1 stehen (überall sonst eine 0). Kategorie \(y\) gibt z.B. an, ob es sich um SPAM (\(y=1\)) handelt oder nicht (\(y=0\)).
Künstliche Neuronale Netze sind inspiriert von biologischen Gehirnen, z.B. das des Menschen oder das der Katze. Die wichtigsten Bestandteile eines biologischen Gehirns sind die Gehirnzellen, auch Neuronen genannt, und die Verbindungen zwischen den Neuronen. Ein wichtiger Teil einer Verbindung ist die Synapse.
Das menschliche Gehirn besteht aus etwa 86 Milliarden Neuronen und ca. \(10^{14}\) (100 Trillionen) Verbindungen, also Synapsen. Zum Vergleich: ein Schimpanse hat 7 Milliarden, eine Katze 250 Millionen, eine Fruchtfliege 100 Tausend Neuronen.
Wir beschäftigen uns hier kurz mit dem Übergang vom biologischen zum künstlichen Neuron.
Die Zahl der Neuronen stammt von Herculano-Houzel (2009).
3.1.1 Biologische Neuronen
Die Neuronen sind die atomaren Einheiten des Gehirns. Neuronen empfangen elektrische Signale über Dendriten und laden sich gewissermaßen auf, man spricht vom Aktionspotential oder Erregung. Erst wenn ein bestimmter Schwellwert erreicht ist, “feuert” das Neuron über das Axon ein Signal nach außen. Beim Feuern wird eine (elektrische) Erregung von einem Neuron auf ein anderes übertragen.
Die Erregung eines Neurons wird über sein Axon weitergegeben und über Synapsen auf die Dendriten anderer Neuronen weitergegeben (Abb. 3.1). Eine Synapse bezeichnet eine Stelle mit einer physikalischen Lücke, die durch Neurotransmitter - das sind chemische Botenstoffe - überbrückt werden. Neurotransmitter können das Signal verstärken (exzitatorisch) oder hemmen (inhibitorisch). Diese Veränderbarkeit der Informationsübertragung spiegelt sich in den Gewichten künstlicher Neuronaler Netze wider.
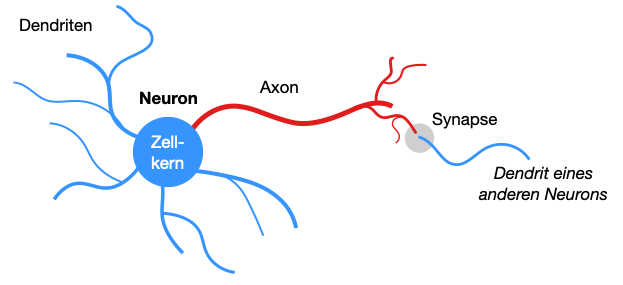
Das ist natürlich eine stark vereinfachte Darstellung der Funktionsweise biologischer Neuronen. Der Wikipedia-Artikel über die Nervenzelle geht etwas mehr ins Detail.
Zu den am besten erforschten Regionen im Gehirn gehört der visuelle Cortex, auf den wir im Kapitel über Konvolutionsnetze noch sprechen werden. Ein besonders interessantes ungeklärtes Phänomen im Gehirn ist die Frage, wie verschiedene Hirnareale sich untereinander koordinieren. Eine Hypothese ist, dass die Frequenz des implusartigen Feuerns der Neuronen damit zusammenhängt. Hier sei der kurze Wikipedia-Artikel zur Functional integration empfohlen. Dies ist auch ein gutes Beispiel für ein Phänomen, das bislang nicht in künstlichen Neuronalen Netzen abgebildet ist.
3.1.2 Künstliche Neuronen
Bereits 1943 schlugen Warren McCulloch und Walter Pitts ein informationstechnisches Modell des biologischen Neurons vor: das McCulloch-Pitts-Neuron (McCulloch and Pitts 1943). Das Modell verarbeitete eingehende Signale durch Aufsummieren und kontrollierte die Weiterleitung durch einen Schwellwert. Es wurde gezeigt, dass die grundlegenden booleschen Operatoren (AND, OR, NOT) realisiert werden können. Ein Aspekt, der noch nicht vorhanden war, war die Frage, wie Lernen funktioniert.
Das Perzeptron (engl. perceptron) hatte bereits ein verfeinertes Modell und vor allem einen Lernalgorithmus (allerdings nur für ein Perzeptron mit einer Schicht). Es wurde 1958 von Frank Rosenblatt in einer Publikation der Öffentlichkeit vorgestellt (Rosenblatt 1958). Er hatte es bereits 1957 in einem technischen Bericht beschrieben (Rosenblatt 1957). 1969 gewann das Perzeptron größere Bekanntheit durch eine Buchpublikation der KI-Pioniere Marvin Minsky und Seymour Papert (1969; 2017). Durch das Buch wurden auch die Grenzen des Perzeptrons (sogenanntes XOR-Problem) bekannt. Das Adaline (ADAptive Linear NEuron) wurde 1960 von Bernard Widrow eingeführt (Widrow 1960). Es handelt sich um eine Parallelentwicklung zu Rosenblatts Perzeptron (laut Widrow and Lehr 1990) und unterscheidet sich lediglich durch eine andere Aktivierungsfunktion, die im Gegensatz zur Stufenfunktion beim Perzeptron differenzierbar ist.
Im weiteren sprechen wir einfach von Neuronalen Netzen (kurz NN) und meinen damit künstliche Neuronale Netze.
Auch wenn künstliche NN von biologischen Neuronen inspiriert sind, ist es doch wichtig festzuhalten, dass die Funktionsweise eines künstlichen NN wenig Rückschlüsse auf das menschliche Denken oder auf die Funktionsweise des menschlichen Hirns zulässt. In einem natürlichen Neuron spielen viele Faktoren (biologische, chemische, physikalische) eine Rolle, die in einem künstlichen Neuronalen Netz nicht modelliert sind. Das Lernverfahren “Backpropagation”, mit dem künstliche NN trainiert werden, hat wenig mit biologischen Vorgängen zu tun. Mit der Frage, inwiefern menschliches Denken mit Hilfe von informationstechnischen Modellen erforscht werden kann, beschäftigt sich die Kognitionswissenschaft. Für Modelle, die von biologischen neuronalen Netzen inspiriert sind, hat sich der Konnektionismus als Unterdisziplin der Kognitionswissenschaften herausgebildet (sehr guter Wikipedia-Artikel).
Lesenswertes zum Thema
- McCulloch-Pitts-Neuron: Wikipedia und Blogartikel
- Perzeptron: Wikipedia
- Adaline: Wikipedia
3.2 Perzeptron
Das Perzeptron ist nach dem McCulloch-Pitts-Neuron der erste Versuch, einen lernendes Netzwerk nach dem Vorbild biologischer Neuronen zu erstellen. Es wurde von Frank Rosenblatt entwickelt und 1958 der Öffentlichkeit vorgestellt. Stark verwandt mit dem Perzeptron ist das ADALINE-Netz von Widrow (1960). Die Inhalte dieses Kapitels sind eine Kombination beider Verfahren. Wir nennen das Netz aber der Einfachheit halber immer Perzeptron.
Das Video erläutert kurz die Funktionsweise eines Perzeptrons.
3.2.1 Modell
Das Perzeptron ist ein Netzwerk aus Neuronen und gerichteten Verbindungen. Die Neuronen sind in Schichten (engl. layers) organisiert, der Eingabeschicht und der Ausgabeschicht. Die Verbindungen laufen von Eingabeschicht zu Ausgabeschicht. Ein solches Netz ist somit ein gerichteter azyklischer Graph (engl. directed acyclic graph, kurz DAG).
Die Ausgabeschicht besteht aus einem einzigen Neuron. Das Netz kann zur binären Klassifikation verwendet werden, d.h. für einen Input \(x\) (wir nennen dies auch Featurevektor, z.B. die Pixel eines Bildes) kann das Netz entscheiden, ob dieser Input zu einer bestimmten Kategorie gehört (Katzenbild) oder nicht (kein Katzenbild). Dies wird entsprechend mit dem Wert \(y \in \{0, 1\}\) ausgedrückt.
Manchmal wird das Perzeptron auch mit der Outputmenge \(y \in \{-1, 1\}\) eingeführt.
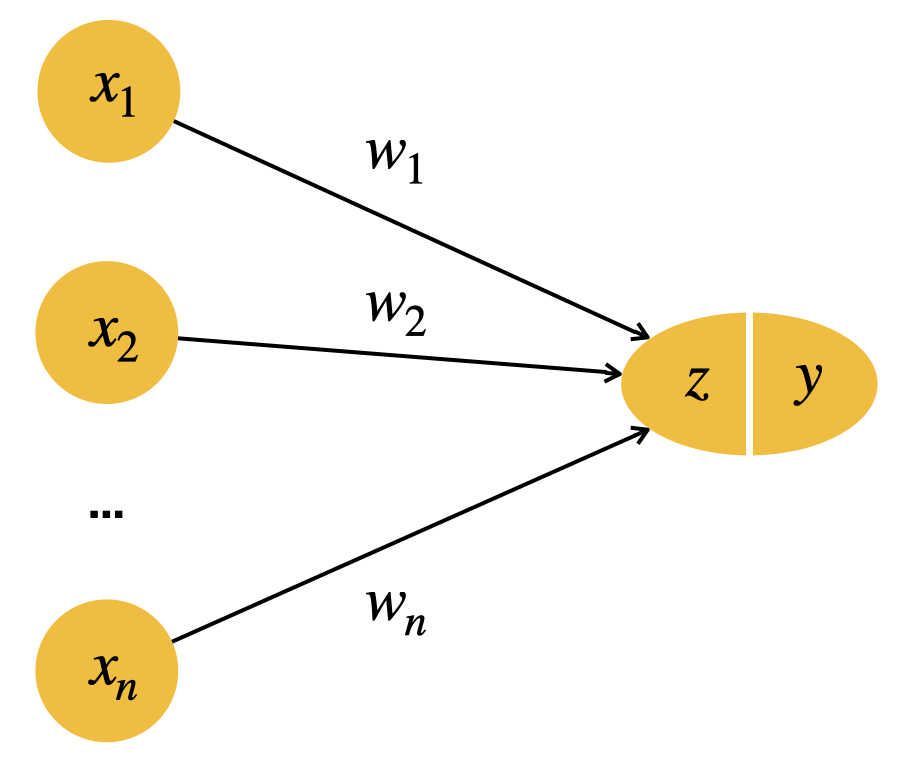
Der Wert \(z\) ist eine “Zwischenberechnung”, der so genannte Rohinput, den wir gleich erklären.
Wir haben gerade von “Schichten” gesprochen. Es zeigt sich, dass es sinnvoll ist, eine Schicht so zu definieren, dass eine Schicht mehrere Parameter/Gewichte enthält. In diesem Sinne hat das Perzeptron nur eine Schicht. Die Eingabe zählt nicht als eigenständige Schicht.

Vektordarstellung
Der Input durch die Eingabeneuronen wird repräsentiert durch einen Vektor \(x = (x_1, \ldots, x_n)\) der Länge \(n\), wobei jedes einzelne Feature \(x_i \in \mathbb{R}\). Auch wenn wir im Text Vektoren oft als Zeilenvektor schreiben, ist in Berechnungen immer ein Spaltenvektor gemeint, d.h. Vektor \(x\) sieht so aus:
\[ x = \left( \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right) \]
Der gewünschte Output am Ausgabeneuron ist ein Skalar \(y\), das entweder 0 oder 1 ist.
Die Parameter des Perzeptrons nennen wir Gewichte (engl. weights). Sie sind ein Vektor \(w\), wobei \(w_i \in \mathbb{R}\). Auch hier gilt in den Berechnungen, dass es sich um einen Spaltenvektor handelt:
\[ w = \left( \begin{array}{c} w_1 \\ \vdots \\ w_n \end{array} \right) \]
3.2.2 Vorwärtsverarbeitung
Wenn wir an den Eingabeneuronen Werte in Form des Vektors \(x\) anlegen, wie wird der Output \(y\) berechnet? Diese Verarbeitungsrichtung nennt man auch Forward Propagation.
Roheingabe
In einem ersten Schritt berechnen wir für einen gegebenen Featurevektor \(x\) die Roheingabe \(z\) (engl. net input) des Ausgabeneurons (siehe Abb. oben). Dies ist die Summe der Werte der Eingabeneuronen, jeweils multipliziert mit den jeweiligen Gewichten.
\[\begin{align*} z & = \sum_{i=1}^n w_i \: x_i\\[3mm] &= w_1 x_1 + \ldots + w_n x_n \end{align*}\]
In Vektorform können wir die Vektoren \(x\) und \(w\) wie folgt multiplizieren:
\[\begin{align*}\tag{Z} z & = w^T x\\[2mm] &= (w_1, \ldots, w_n) \left( \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right) \\[3mm] &= w_1 x_1 + \ldots + w_n x_n \end{align*}\]
Vektor \(w^T\) ist dabei der transponierte Vektor von \(w\) und daher ein Zeilenvektor. Nur so ist die Multiplikation zulässig (wir sehen hier alles als Matrizenmultiplikation).
Aktivierung und Output
Im zweiten Schritt berechnen wir die Aktivierung \(y\) des Ausgabeneurons. Dies ist gleichzeitig der Gesamtoutput des Neuronalen Netzes.
Die Aktivierung wird berechnet, indem wir eine Aktivierungsfunktion \(g\) auf die Roheingabe \(z\) anwenden.
\[ \tag{Y} y = g(z) \]
Für \(g\) verwenden wir die sogenannte Heaviside- oder Stufenfunktion (auch step oder threshold function):
\[ g_\theta(z) = \begin{cases} 1 & \quad \text{falls } z \geq \theta \\[3mm] 0 & \quad \text{sonst} \end{cases} \]
wobei \(\theta\) (griech. Buchstabe Theta) auch der Schwellwert (engl. threshold) genannt wird.
Wenn der Schwellwert \(\theta = 0\) ist, sieht die Aktivierungsfunktion so aus:
x = [-10, -5, 0, 0, 5, 10]
y = [0, 0, 0, 1, 1, 1]
plt.plot(x,y,'r')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Heaviside-Aktivierungsfunktion')
plt.xticks([-10,-5,0,5,10])
plt.yticks([0,.5,1])
plt.grid()
plt.show()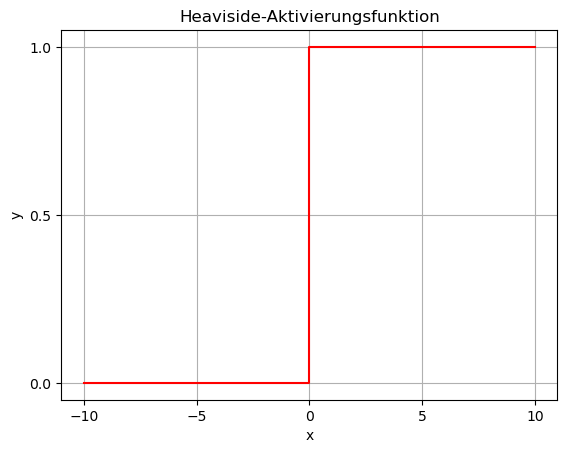
Diese Funktion ist nicht differenzierbar bei \(x = 0\).
Modellierung des logischen AND
Das Perzeptron kann grundlegende logische Operationen nachbilden. Wir können etwa den logischen Operator AND mit einem Perzeptron modellieren:

Bei einem AND haben wir einen sehr überschaubaren Datensatz:
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Ein Perzeptron mit den folgenden Parametern und Schwellwert leistet genau die gewünscht Operation:
\[\begin{align*} w_1 &= 1\\ w_2 &= 1\\ \theta &= 2 \end{align*}\]
Modellierung des logischen OR
Ähnlich wie mit dem AND verhält es sich mit dem OR. Hier der Datensatz:
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Im Vergleich zum AND-Perzeptron kann man z.B. einfach den Schwellwert absenken:
\[\begin{align*} w_1 &= 1\\ w_2 &= 1\\ \theta &= 1 \end{align*}\]
Es gibt natürlich noch weitere Lösungen für AND und OR.
Das Video zeigt die Realisierung des OR im Perzeptron.
XOR
Wenn Sie probieren, das XOR mit diesem Netz zu lösen, werden Sie feststellen, dass es nicht geht. Hier der dazugehörige Datensatz:
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Dies zeigten auch 1969 Marvin Minsky und Seymour Papert in ihrem Buch Perceptrons: an introduction to computational geometry (Minsky and Papert 1969).
Man benötigt für das XOR eine weitere Schicht. Probieren Sie doch mal, ein solches Netz zu entwerfen. Vergessen Sie nicht, Gewichte und Schwellwert anzugeben.
Bias-Neuron
Der Schwellwert \(\theta\) ist etwas umständlich für weitere Berechnungen. Deshalb versuchen wir, ihn leicht zu verschieben.
Unsere Aktivierungsfunktion \(g\) prüft, ob
\[ z = w_1 x_1 + \ldots + w_n x_n \geq \theta \]
Jetzt können wir das \(\theta\) auf die andere Seite holen:
\[ -\theta + w_1 x_1 + \ldots + w_n x_n \geq 0 \]
Wir erweitern jetzt einfach die Vektoren \(x\) und \(w\) um jeweils eine Stelle mit Index \(0\). Dabei ist \(x_0 = 1\) und \(w_0 = -\theta\):
\[ w_0 x_0 + w_1 x_1 + \ldots + w_n x_n \geq 0 \]
Man nennt das Neuron \(x_0\), das immer gleich \(1\) ist, auch das Bias-Neuron.
Jetzt können wir die Funktion \(g\) immer mit Null als Schwellwert formulieren:
\[ g(z) = \begin{cases} 1 & \quad \text{falls } z \geq 0 \\ 0 & \quad \text{sonst} \end{cases} \]
Die Formeln (Z) und (Y) können wir einfach so beibehalten in dem Wissen, dass die Komponente 0 in \(x\) immer gleich eins ist.
Unser Netz sieht mit Bias-Neuron jetzt so aus:
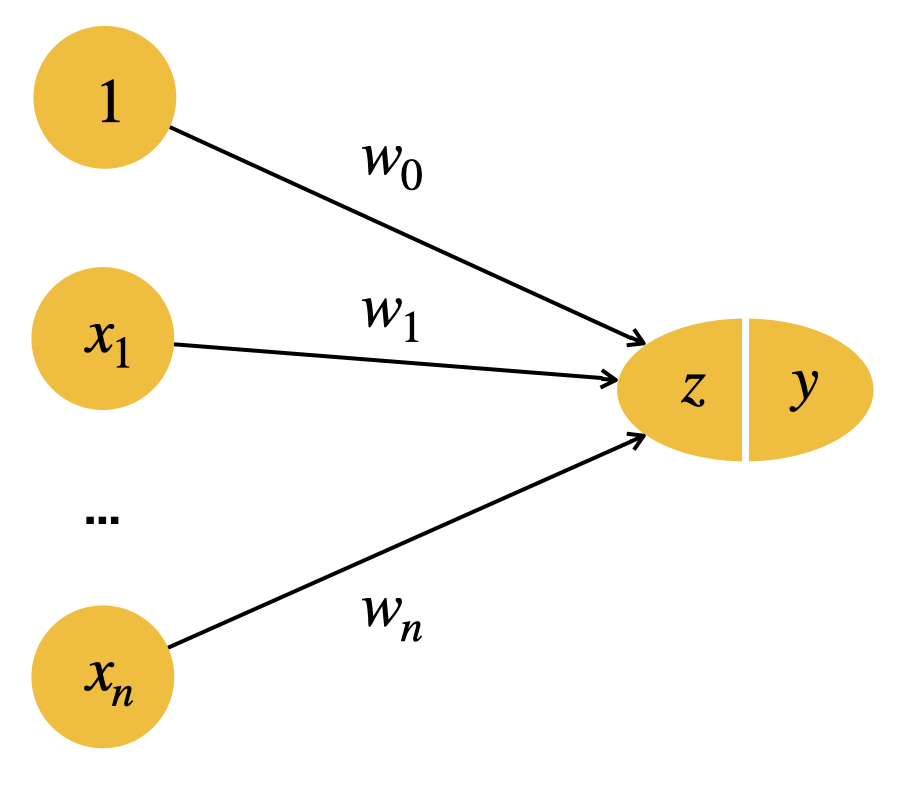
Das Video erläutert die Herleitung des Bias-Neurons.
3.2.3 Klassifikation mit mehr als zwei Klassen
Bei der obigen Herleitung handelt es sich um binäre Klassifikation mit einem Output \(\in [0, 1]\) und einem Schwellwert. Wie können wir eine Klassifizierung für drei oder mehr Klassen erreichen?
Im nächsten Kapitel werden wir neuronale Netze betrachten, die auf “ganz natürliche Weise” einen Mehrklassen-Output haben, aber hier möchte ich kurz eine generelle Denkweise vorstellen für den Fall, dass wir nur binäre Klassifikatoren zur Verfügung haben wie bei einem Perzeptron.
Die Grundidee ist, dass man bei mehreren (\(N\)) Klassen \(i\in{1,\ldots,N}\) für jede Klasse \(i\) einen eigenen binären Klassifikator \(h_w^{(i)}\) erstellt. Bei drei Klassen hätten wir also drei Klassifikatoren \(h_w^{(1)}, h_w^{(2)},h_w^{(3)}\), hier als drei Perzeptronen realisiert:
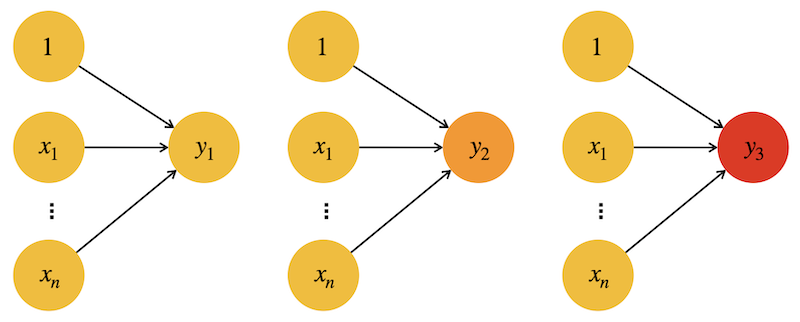
Die Trainingsdaten werden für jeden binären Klassifikator entsprechend präpariert: Für Klassifikator \(h_w^{(1)}\) nimmt man alle Trainingsbeispiele der Klasse 1 als Positivbeispiele (\(y=1\)) und alle anderen als Negativbeispiele (\(y=0\)). Entsprechend für die anderen drei Klassifikatoren.
Um eine Vorhersage auf Eingabedaten \(x\) zu erhalten, steckt man \(x\) in alle Klassifikatoren \(h_w^{(i)}\) und wählt die Klasse des Klassifikators mit dem höchsten Ausgabewert.
\[ \underset{i}{\arg \max} \, h_w^{(i)}(x) \]
Diese Methode nennt man auch One-vs-All (OvA) oder One-vs-Rest.
Tatsächlich kann man sich auch ein einziges Netz mit drei Output-Neuronen vorstellen:
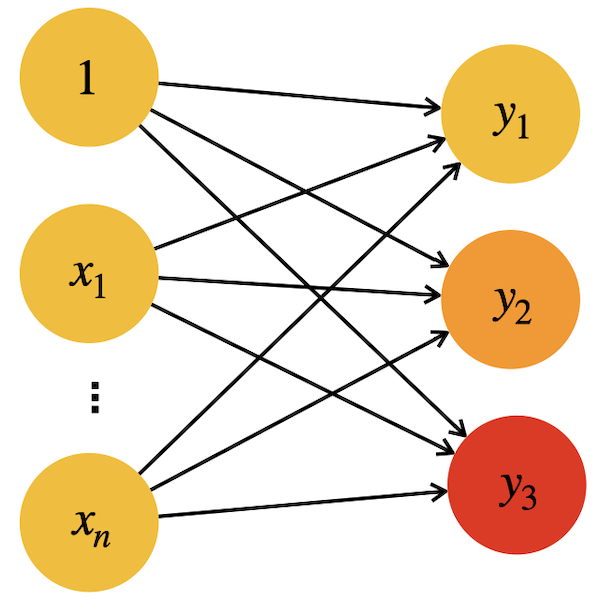
Das Output-Neuron mit der höchsten Aktivierung “gewinnt” und die entsprechende Klasse zählt aus Ausgabe.
Die Funktion arg max funktioniert wie folgt. Sie bekommt eine Funktion mit einem Parameter und gibt den Parameterwert zurück, mit dem die Funktion maximal wird. Beispiel: Einen Vektor \(v = (v_1, \ldots, v_4)\) kann man auch als Funktion über seine Indizes betrachten. In diesem Fall gibt arg max den Index des Vektorelements mit dem höchsten Wert zurück. Als Beispiel sei Vektor \(v = (5, 2, 18, -3)\) gegeben; dann ist \(\underset{i}{\arg \max} \, v_i = 3\).
3.2.4 Einfaches Perzeptron in Python
Wir sehen uns an, wie wir die Funktionsweise eines einfaches Perzeptrons in Python mit Hilfe von NumPy realisieren würden.
Zuerst erstellen wir einen Eingabevektor
\[ x = \left( \begin{array}{c} 0 \\ 1 \end{array} \right) \]
als NumPy-Array (siehe auch Abschnitt 1.1.4).
x = np.array([0, 1])Dann einen Vektor
\[ w = \left( \begin{array}{c} 1 \\ 1 \end{array} \right) \]
mit den Gewichten:
w = np.array([1, 1])Die Aktivierung \(z\) können wir mit dem Skalarprodukt berechnen:
\[ z := w^T \cdot x = ( 1 \quad 1 ) \left( \begin{array}{c} 0 \\ 1 \end{array} \right) = 1 \cdot 0 + 1 \cdot 1 = 1 \]
z = w.dot(x)
z1Wir können auch den Operator @ verwenden:
z = w @ x
z1Ob die Aktivierung größer-gleich dem Schwellwert 1 ist, können wir so testen:
z >= 1TrueFunktion für ein Perzeptron
Für eine beliebige Konfiguration von Eingabe, Gewichten und Schwellwert können wir eine Funktion schreiben. Es muss nur sichergestellt werden, dass \(x\) und \(w\) die gleiche Länge haben.
def perceptron_process(x, w, theta):
return w @ x >= thetaWir testen das Beispiel von oben:
perceptron_process(x, w, 1)TrueAND- und OR-Netze
Wir können jetzt die Netze für AND und OR nachbauen. Zunächst bilden wir alle vier möglichen Inputvektoren:
x1 = np.array([0, 0])
x2 = np.array([0, 1])
x3 = np.array([1, 0])
x4 = np.array([1, 1])Wir definieren Gewichte und Schwellwert für AND und testen unser Netz:
w_and = np.array([1, 1])
theta_and = 2
print(perceptron_process(x1, w_and, theta_and))
print(perceptron_process(x2, w_and, theta_and))
print(perceptron_process(x3, w_and, theta_and))
print(perceptron_process(x4, w_and, theta_and))False
False
False
TrueDas sieht korrekt aus!
Das gleiche für OR:
w_or = np.array([1, 1])
theta_or = 1
print(perceptron_process(x1, w_or, theta_or))
print(perceptron_process(x2, w_or, theta_or))
print(perceptron_process(x3, w_or, theta_or))
print(perceptron_process(x4, w_or, theta_or))False
True
True
TrueEffiziente Verarbeitung mit einer Matrix
Jetzt packen wir alle vier Input-Vektoren in eine Matrix
\[ X = \begin{pmatrix} 0 & 0\\ 0& 1 \\ 1& 0 \\ 1 & 1 \end{pmatrix} \]
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
Xarray([[0, 0],
[0, 1],
[1, 0],
[1, 1]])Jetzt kommt das Kunststück: Für eine einzelne Eingabe nehmen wir das Skalarprodukt von Eingabevektor und Gewichtsvektor. Für mehrere Eingaben, die in eine Matrix verpackt sind, können wir alle Eingaben “parallel” mit einer einzigen Matrixmultiplikation berechnen und erhalten die vier Resultate (Rohinputs) in einem Vektor:
\[ X \cdot w_{and} = \begin{pmatrix} 0 & 0\\ 0& 1 \\ 1& 0 \\ 1 & 1 \end{pmatrix} \left( \begin{array}{c} 1 \\ 1 \end{array} \right) = \left( \begin{array}{c} 0 \\ 1 \\ 1\\ 2 \end{array} \right)\]
X @ w_andarray([0, 1, 1, 2])Jetzt können wir jedes Element wieder mit dem Schwellwert vergleichen, um die finale Aktivierung pro Eingabe zu bekommen.
Einmal für AND:
X @ w_and >= theta_andarray([False, False, False, True])Und für OR:
X @ w_or >= theta_orarray([False, True, True, True])Sie ahnen hier vielleicht schon, dass das “Verpacken” von Trainingsdaten in eine Matrix zu sehr eleganten (und tatsächlich auch effizienten) Berechnungen führt.
Falls Sie der Operator @ in den Beispielen oben verwirrt. Es handelt sich über eine Abkürzung für die Funktion matmul bzw. für die Funktion dot. Siehe auch Abschnit 1.1.4.
3.3 Lernen mit dem Perzeptron
Lernen bedeutet, dass die Gewichte \(w\) mit Hilfe von Trainingsdaten schrittweise angepasst werden, so dass unser Netzwerk sich der gewünschten idealen Funktion \(h^*\) annähert. Trainingsdaten sind z.B. eine Reihe von Bildern mit Labeln (z.B. Katze und Nicht-Katze). Wir gehen von \(N\) Traningsdaten aus und verwenden \(k \in \{1,\ldots , N\}\) als Index für ein Trainingsbeispiel. Für \(N\) Traningsdaten schreiben wir die Paare bestehend aus einem Featurevektor \(x\) und einem Label \(y\) so:
\[(x^k, y^k) \quad\quad k \in \{1,\ldots , N\}\]
Bei \(y^k\) handelt es sich um den korrekten Output des Trainingsbeispiels. Wenn wir aber für \(x^k\) den Output im aktuellen Neuronalen Netz berechenen, erhalten wir den berechneten Output.Wir schreiben:
- \(\hat{y}^k\) für den berechnete Ouput des aktuellen Netzwerks für Trainingsbeispiel \(k\) mit Forward Propagation
- \(y^k\) für den korrekten Output des Trainingsbeispiels \(k\)
Sowohl \(y\) als auch \(\hat{y}\) sind aus der Menge \(\{0,1\}\).
Lernen bedeutet, dass wir für jedes Trainingsbeispiel \(k\) den Output \(\hat{y}^k\) berechnen und die Gewichte so anpassen, dass der Fehler, also die Differenz zwischen berechnetem und korrekten Output, kleiner wird. Dazu addieren wir auf jedes Gewicht ein “Delta”. Das nennt man auch ein Update.
Für ein Trainingsbeispiel \((x^k, y^k)\) führen wir für alle Gewichte \(w = (w_0, \ldots, w_n)\) ein Update durch, indem wir zu jedem \(w_i\) ein \(\Delta w_i\) addieren:
\[ w_i := w_i + \Delta w_i \]
Im Folgenden leiten wir her, wie dieses \(\Delta w_i\) genau aussieht.
3.3.1 Gradientenabstieg
Unsere Herleitung folgt der Idee des Gradientenabstieg und dieses Verfahren bedeutet etwas ganz Einfaches: Wenn wir einen Parameter \(w\) haben und diesen leicht vergrößern, wird dann der Fehler kleiner oder größer? Diese Frage wird genau mit dem Gradienten beantwortet und erlaubt uns die zielgerichtete Anpassung von \(w\).
Für unsere Herleitung ist es leichter, wenn wir als Aktivierungsfunktion \(g\) die Identität nehmen, also:
\[ \tag{A} g(z) = z \]
Sie erinnern sich: Das originale Perzeptron hat hier die Heaviside-Funktion. Der entscheidende Unterschied ist, dass die Identitäts-Funktion differenzierbar ist, d.h. man kann eine Ableitung bilden. Dies ist für das Verfahren des Gradientenabstiegs wesentlich.
Man beachte, dass die berechnete Ausgabe \(\hat{y} = g(z) = z\) jetzt eine Dezimalzahl \(\in \mathbb{R}\) ist, da wir den Rohinput einfach “durchschleifen”. Zuvor hatten wir die Ausgabe in die Form 0 oder 1 gezwungen.
Verlustfunktion
Dazu müssen wir die Abweichung zwischen den berechneten Ouputs und den korrekten Outputs berechnen. Dies tut man über eine Zielfunktion \(J\). Diese wird auch Verlustfunktion oder Fehlerfunktion genannt, im Englischen meistens loss function.
Wir folgen hier der Literatur, wo die Fehlerfunktion sehr oft mit dem Buchstaben \(J\) repräsentiert wird. Das hängt vermutlich mit dem Konzept der Jacobi-Matrix zusammen. Die Jacobi-Matrix einer Funktion \(f\) enthält alle partiellen Ableitungen von \(f\). Insofern ist die Benennung der Fehlerfunktion mit \(J\) nicht ganz logisch, weil wir später die Jacobi-Matrix von \(J\) betrachten und diese dann \(\nabla J\) heißt.
Für unser \(J\) wählen wir den Mittelwert der Fehlerquadrate (engl. mean of squared errors oder MSE). Der Faktor \(\frac{1}{2}\) dient nur der Kosmetik (weil sich die 2 im Nenner bei der Ableitung herauskürzt) und beeinträchtigt nicht den Nutzen von \(J\):
\[ \tag{J} J(w) = \frac{1}{2N} \sum_{k=1}^N \left( y^k - \hat{y}^k \right)^2 \]
Vergegenwärtigen Sie sich, dass dieser Fehler in der Hauptsache davon abhängt, in welcher “Konfiguration” sich das Netz befindet, also wie die Gewichte \(w\) eingestellt ist. Wir sind daran interessiert, die Gewichte so einzustellen, dass der Gesamtfehler \(J\) möglichst klein wird. Im Training soll das automatisiert ablaufen.
Diese Abhängigkeit von \(w\) zu \(J\) spannt eine Fehlerlandschaft auf. Bei dem Beispiel in Abbildung 3.2 kann man sich zwei beliebige Gewichte (z.B. \(w_0\) und \(w_1\)) als 2-dimensionale Ebene vorstellen, wohingegen der Fehlerwert \(J\) nach oben zeigt. Da wir einen möglichst geringen Fehler anstreben, suchen wir also nach dem tiefsten Tal.
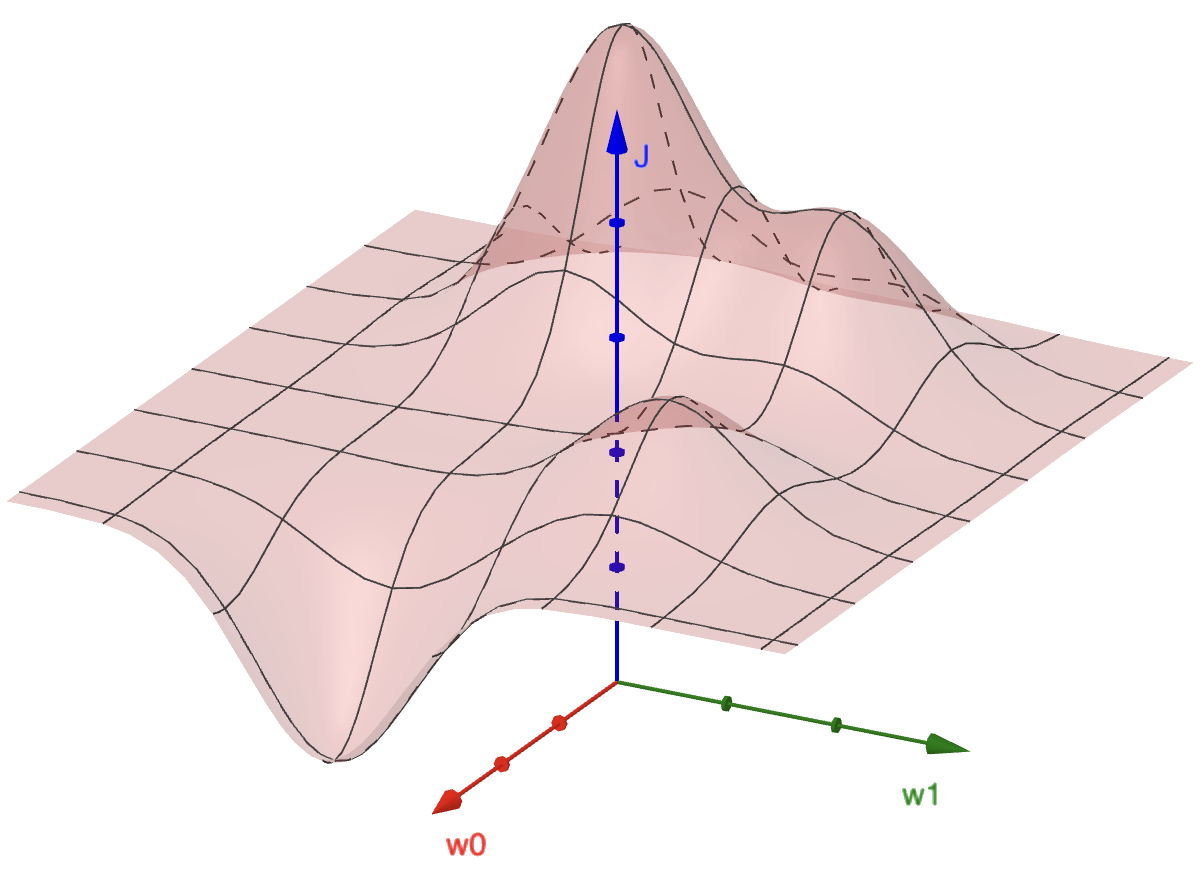
Update der Gewichte
Jetzt kommt der Gradientenabstieg zum Zug. Wir wollen die Gewichte so anpassen, dass der Fehler sich verringert. Dazu gehen wir in Richtung des negativen Gradienten, denn der Gradient gibt uns den größten Anstieg. Den Verlauf der Updates kann man sich anhand der Fehlerlandschaft so vorstellen wie in Abbildung 3.3.
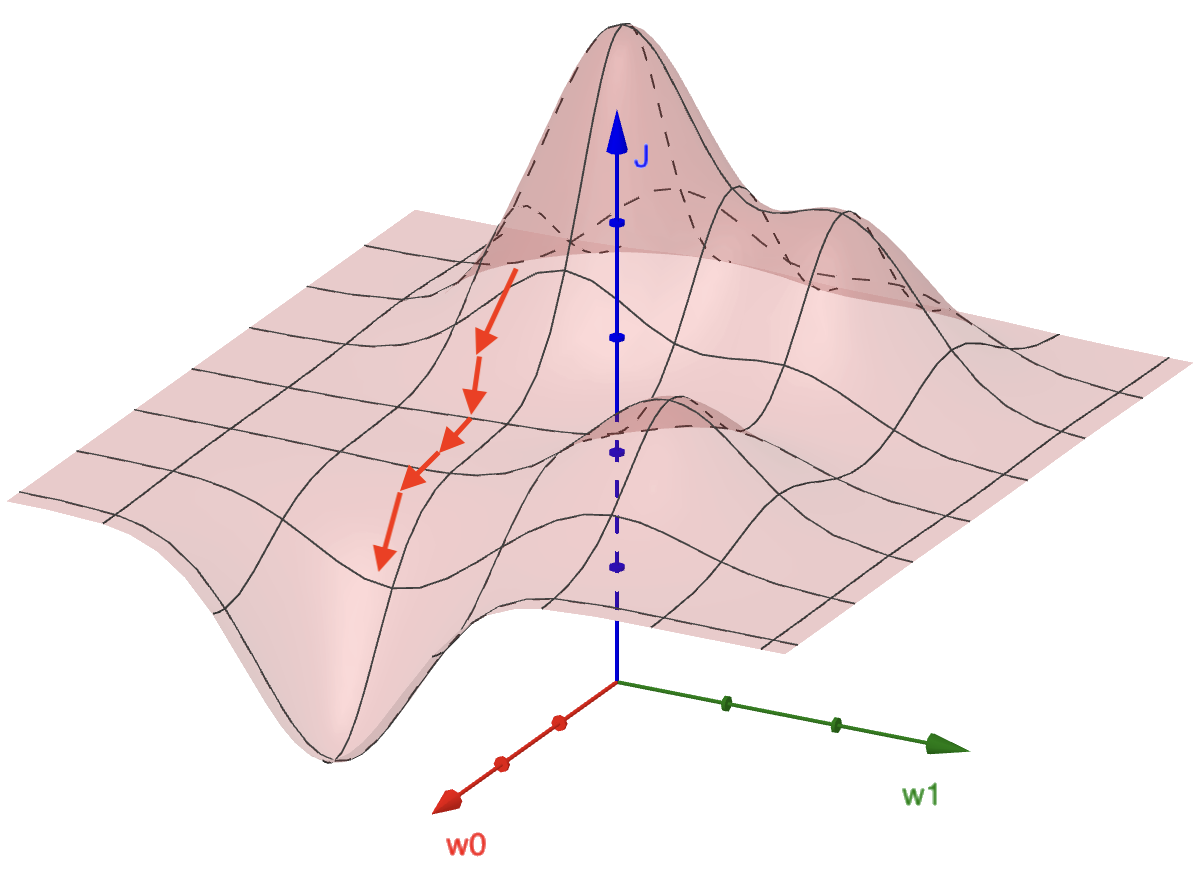
Wir formulieren das Update der Gewichte mit Vektoren:
\[ w := w + \Delta w \]
Aufgrund der obigen Ausführungen können wir das Delta definieren als den negativen Gradienten des Fehlers \(J\) definieren. Wir schwächen diesen Gradienten noch durch eine sogenannte Lernrate \(\alpha\) ab (zwischen 0 und 1):
\[ \Delta w := - \alpha \nabla J(w) = - \alpha \left( \begin{array}{c} \frac{\partial J}{\partial w_1} (w) \\ \vdots \\ \frac{\partial J}{\partial w_n} (w) \end{array} \right) \]
Denken Sie immer daran, dass sich die Gewichte \(w\) im Verlauf des Trainings ändern. Das \(w\) in dem Ausdruck \(-\alpha \nabla J(w)\) soll deutlich machen, dass wir in die Ableitungen immer konkrete Werte im Form des Gewichtsvektors \(w\) einsetzen. Die Gewichte sind sozusagen die “aktuelle Konfiguration” des Netzwerks (in der Abbildung oben ist das ein Punkt in der Ebene, die von \(w_0\) und \(w_1\) aufgespannt wird). Die Ableitungen \(\frac{\partial J}{\partial w_i} (w)\) sind ebenfalls Funktionen mit Parameter \(w\) und werden an der aktuellen Stelle \(w\) evaluiert.
Wie man in der Gleichung oben sieht, benötigen wir für \(\nabla J\) alle partiellen Ableitungen von \(J\) hinsichtlich der Einzelgewichte \(w_1, \ldots, w_n\).
Für eine einzelne partielle Ableitung des Gradienten gilt:
\[ \tag{G} \frac{\partial J}{\partial w_i} (w) = - \frac{1}{N} \sum_{k=1}^N \left( y^k - g(z^k) \right) x_i^k \]
Gesucht: Wir suchen alle partiellen Ableitungen von \(J\), also \(\frac{\partial J}{\partial w_i}\) für alle \(i\in {0, \ldots, n}\).
Ausgangspunkt ist die Fehlerfunktion (J), die wir erstmal umformen.
\[ J(w) = \frac{1}{2N} \sum_{k=1}^N \left( y^k - g(z^k) \right)^2 \]
Da \(g\) die Identitätsfunktion ist (A):
\[ J(w) = \frac{1}{2N} \sum_{k=1}^N \left( y^k - z^k \right)^2 \]
Jetzt setzen wir \(z^k\) ein, wie in (Z) definiert:
\[ J(w) = \frac{1}{2N} \sum_{k=1}^N \left( y^k - w^T x^k \right)^2 \]
Jetzt können wir \(\frac{\partial J}{\partial w_i}\) berechnen:
\[\begin{align*} \frac{\partial J}{\partial w_i} & = \frac{\partial}{\partial w_i} \frac{1}{2N} \sum_{k=1}^N \left( y^k - w^T x^k \right)^2 \\[2mm] &= \frac{1}{2N} \sum_{k=1}^N \frac{\partial}{\partial w_i} \left( y^k - w^T x^k \right)^2\\[2mm] &= \frac{1}{2N} \sum_{k=1}^N 2 \left( y^k - w^T x^k \right) \frac{\partial}{\partial w_i} - w^T x^k\\[2mm] &= - \frac{1}{N} \sum_{k=1}^N \left( y^k - w^T x^k\right) x_i^k \\[2mm] &= - \frac{1}{N} \sum_{k=1}^N \left( y^k - g(z^k) \right) x_i^k \end{align*}\]
Damit wäre (G) gezeigt.
Für ein einzelnes Gewicht \(w_i\) sieht das Delta entsprechend wie folgt aus:
\[\begin{align*} \Delta w_i &= - \alpha \frac{\partial J}{\partial w_i} (w) \\[1mm] &= \alpha \frac{1}{N} \sum_{k=1}^N \left( y^k - g(z^k) \right) x_i^k \\[1mm] &= \alpha \frac{1}{N} \sum_{k=1}^N \left( y^k - \hat{y}^k \right) x_i^k \end{align*}\]
Die Lernrate \(\alpha\) wird zwischen 0 und 1 gewählt und bestimmt, wie schnell das Lernen stattfindet. Eine zu hohe Lernrate kann dazu führen, dass das Optimum immer wieder “übersprungen” wird, so dass das Lernen doch wieder langsamer wird oder sogar nie das Optimum erreicht. Eine zu niedrige Lernrate kann zu sehr langsamen Lernprozessen führen. Als Daumenregel sollte man mit niedrigen Lernraten beginnen und diese dann schrittweise erhöhen. Erfahrungsgemäß funktionieren Lernraten zwischen \(0.1\) und \(0.3\) gut als Startpunkt.
Wie man an dem Summenzeichen sieht, wird ein Update erst nach Abarbeiten aller Trainingsdaten durchgeführt. Das heißt übrigens, dass wir die Deltas für jedes Trainingsbeispiel aufaddieren müssen, um dann am Schluss das finale Delta auf ein Gewicht anzuwenden.
Wir sehen uns die Update-Regel für ein einzelnes Gewicht an:
\[ w_i := w_i + \alpha \frac{1}{N} \sum_{k=1}^N \left( y^k - \hat{y}^k \right) x_i^k \]
Wir können uns unabhängig von der Herleitung überlegen, ob die obige Rechnung plausibel ist. Nehmen wir einmal an, es gäbe nur ein Traningsbeispiel, d.h. wir vergleichen hauptsächlich \(y^k\) mit \(\hat{y}^k\).
Die Vereinfachung für ein einziges Trainingsbeispiel kann man sich so vorstellen:
\[ w_i := w_i + \alpha \left( y - \hat{y} \right) x_i \]
Was beobachten wir?
- Wenn die berechnete Ausgabe \(\hat{y}\) und die korrekte Ausgabe \(y\) gleich sind, wird quasi kein Update durchgeführt, denn das Gewicht bleibt gleich.
- Wenn die berechnete Ausgabe \(\hat{y}\) größer ist als die korrekte Ausgabe \(y\), dann wird die Änderung negativ, also wird das Gewicht abgeschwächt. Wie stark sich das Gewicht verkleinert, hängt von der Differenz von korrekter und berechneter Ausgabe ab und, genauso wichtig, vom Wert \(x\). Das \(x\) zeigt nämlich an, wie relevant diese Verbindung für die Ausgabe war (im Extremfall war \(x\) gleich Null, dann lohnt sich eine Änderung nicht). Insgesamt wird \(\hat{y}\) beim “nächsten Mal” kleiner und damit näher an der korrekten Ausgabe sein.
- Wenn die berechnete Ausgabe \(\hat{y}\) kleiner ist als die korrekte Ausgabe \(y\), dann wird die Änderung positiv, d.h. das Gewicht wird gestärkt. Dies wird wie im obigen Fall moduliert durch Differenz und Stärke von \(x\). Insgesamt wird \(\hat{y}\) beim “nächsten Mal” größer und damit näher an der korrekten Ausgabe sein.
Man beachte, dass für das Gewicht des Bias-Neurons \(x_0\) gilt:
\[ w_0 := w_0 + \alpha \left( y - \hat{y} \right) \]
da \(x_0 = 1\).
3.3.2 Lernalgorithmus
Angesichts unserer Herleitung formulieren wir einen Lernalgorithmus. Man beachte, dass wir das \(\Delta w_i\) innerhalb einer Epoche als Speicher benutzen, um alle Deltas für alle Trainingsdaten “einzusammeln” (zu aggregieren). Wir benutzen Variable \(S\), um die Fehlerwerte zu aggregieren.
Hier nochmal die zwei wichtigen Formeln (Fehler und Update):
\[ \begin{align*} J &:= \frac{1}{2N} \sum_{k=1}^N \left( y^k - \hat{y}^k \right)^2 \\ w_i &:= w_i + \alpha \frac{1}{N} \sum_{k=1}^N \left( y^k - \hat{y}^k \right) x_i^k \end{align*} \]
wobei \(i \in \{1, \ldots, n\}\)
Initialisierung:
Setze alle Gewichte \(w = (w_0, \ldots, w_n)\), z.B. auf 0 oder auf niedrige Zufallswerte
Für jede Epoche: (= Durchlauf aller Trainingsbeispiele)
- setze \(\Delta w_i := 0\) und \(S := 0\)
- Für jedes Trainingsbeispiel \((x^k, y^k)\), \(k = 1,\ldots, N\):
- berechne den Output \(\hat{y}^k\)
- berechne und aggregiere Deltas \(\Delta w_i := \Delta w_i + (y^k - \hat{y}^k)\, x_i^k\) für \(i \in \{1, \ldots, n\}\)
- berechne und aggregiere Fehler \(S := S + (y^k - \hat{y}^k)^2\)
- führe ein Update aller Gewichte durch mit \(w_i := w_i + \alpha \frac{1}{N} \Delta w_i\) für \(i \in \{1, \ldots, n\}\) (hier wird die Lernrate angewandt und gemittelt)
- berechne Mittelwert aller Fehlerwerte \(J :=\frac{1}{2N} S\) dieser wird zusammen mit der jeweiligen Epoche gespeichert
Wie viele Epochen zum Training genutzt werden, ist dem Anwender überlassen. In der Regel wählt man eine Epochenzahl, z.B. 10 oder 100, und betrachtet die Fehlerentwicklung über die Epochen, um zu entscheiden, ob man länger trainieren sollte.
Der hier berechnete Fehler gilt zu Beginn der jeweiligen Epoche (als vor dem Gewichtsupdate), da man diesen bei der Berechnung der Deltas quasi “geschenkt” bekommt, denn bei beiden Rechnungen benötigt man \((y^k - \hat{y}^k)\). Daher sieht man beim Training den Fehler vor der Gewichtsanpassung, was vielleicht kontraintuitiv ist, aber effizienter ist, als den Fehler am Ende der Epoche nochmal zu berechnen.
3.4 Implementierung in Python
Wir implementieren das Perzeptron in Python, um die Funktionsweise besser zu verstehen. Zum Training verwenden wir die Iris-Daten und zeigen, wie man die Daten für eine binäre Klassifikation vorbereitet.
3.4.1 Iris-Datensatz
Im Iris-Datensatz geht es darum, eine Blume aufgrund der Abmessungen ihrer Blüte zu klassifizieren. Es gibt drei Blumen-Klassen, die es vorherzusagen gilt: iris setosa, iris virginica und iris versicolor. Es gibt vier Blüten-Abmessungen als Eingabe-Features für den Input: sepal length, sepal width, petal length und petal width (“sepal” ist das Kelchblatt und “petal” das Kronblatt, siehe Wikipedia). Der Datensatz enthält 150 Trainingsbeispiele, 50 pro Klasse.
Der für den Einstieg sehr beliebte, sehr kleine Iris-Datensatz stammt aus dem Jahr 1936. Bei diesem Datensatz geht es um Blumen, genauer gesagt um die Gattung der “Schwertlilien”, deren lateinischer Name Iris lautet. Der Datensatz besteht nur aus 150 Trainingsbeispielen. Siehe auch den Wikipedia-Artikel.
In den Daten geht es um die Unterscheidung von drei Klassen von Schwertlilien:
- Klasse 0: iris setosa
- Klasse 1: iris virginica
- Klasse 2: iris versicolor
Wir nutzen nur die ersten zwei Klassen 0 und 1 und können somit ein binäres Klassifikationsproblem erzeugen.
Als Features wurden vier Eigenschaften der Blüte gemessen (“sepal” ist das Kelchblatt und “petal” das Kronblatt; siehe Wikipedia):
- Feature 0: sepal length
- Feature 1: sepal width
- Feature 2: petal length
- Feature 3: petal width
Wir nutzen zur Vereinfachung nur zwei Features (Features 0 und 2), da man zwei Features besser visualisieren kann.
Daten laden und vorbereiten
In der Sammlung sind 150 Dateneinträge, jeweils 50 pro Klasse. Jeder Eintrag besteht aus einem Inputvektor der Länge 4 und einer Zahl 0, 1, 2 für die Klasse.
Wir laden die Daten aus der Bibliothek Scikit-learn.
from sklearn import datasets
iris = datasets.load_iris()Wir erhalten ein Dictionary (Hashtabelle) und sehen uns die Schlüssel an:
iris.keys()dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])Die Featurevektoren sind in data, die Labels in der Spalte target.
Wir prüfen den Umfang des Datensatzes:
len(iris.data)150Jetzt schauen wir uns die ersten drei Featurevektoren an:
iris.data[:3]array([[5.1, 3.5, 1.4, 0.2],
[4.9, 3. , 1.4, 0.2],
[4.7, 3.2, 1.3, 0.2]])Und werfen noch einen Blick auf die Label, die mit 0, 1, 2 kodiert sind:
iris.targetarray([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])Diese Zahlen bilden den Index für den Array von Klassennamen. Das stellt sicher, dass kein Fehler bei der Zuordnung von Zahl und Klasse unterläuft.
iris.target_namesarray(['setosa', 'versicolor', 'virginica'], dtype='<U10')Das gleiche gilt für die Bezeichnungen und die Reihenfolge der vier Features:
iris.feature_names['sepal length (cm)',
'sepal width (cm)',
'petal length (cm)',
'petal width (cm)']Daten auf zwei Features beschränken
Für unser Beispiel möchten wir nur zwei Features verwenden:
- sepal length (Index 0)
- petal length (Index 2)
Dazu transponieren wir die Daten, dann erhalten wir vier Vektoren mit jeweils allen Daten für ein Feature.
features = iris.data.T
features[0][:50]array([5.1, 4.9, 4.7, 4.6, 5. , 5.4, 4.6, 5. , 4.4, 4.9, 5.4, 4.8, 4.8,
4.3, 5.8, 5.7, 5.4, 5.1, 5.7, 5.1, 5.4, 5.1, 4.6, 5.1, 4.8, 5. ,
5. , 5.2, 5.2, 4.7, 4.8, 5.4, 5.2, 5.5, 4.9, 5. , 5.5, 4.9, 4.4,
5.1, 5. , 4.5, 4.4, 5. , 5.1, 4.8, 5.1, 4.6, 5.3, 5. ])Jetzt picken wir uns die zwei Features 0 und 2 heraus:
features = features[[0,2]]
featuresarray([[5.1, 4.9, 4.7, 4.6, 5. , 5.4, 4.6, 5. , 4.4, 4.9, 5.4, 4.8, 4.8,
4.3, 5.8, 5.7, 5.4, 5.1, 5.7, 5.1, 5.4, 5.1, 4.6, 5.1, 4.8, 5. ,
5. , 5.2, 5.2, 4.7, 4.8, 5.4, 5.2, 5.5, 4.9, 5. , 5.5, 4.9, 4.4,
5.1, 5. , 4.5, 4.4, 5. , 5.1, 4.8, 5.1, 4.6, 5.3, 5. , 7. , 6.4,
6.9, 5.5, 6.5, 5.7, 6.3, 4.9, 6.6, 5.2, 5. , 5.9, 6. , 6.1, 5.6,
6.7, 5.6, 5.8, 6.2, 5.6, 5.9, 6.1, 6.3, 6.1, 6.4, 6.6, 6.8, 6.7,
6. , 5.7, 5.5, 5.5, 5.8, 6. , 5.4, 6. , 6.7, 6.3, 5.6, 5.5, 5.5,
6.1, 5.8, 5. , 5.6, 5.7, 5.7, 6.2, 5.1, 5.7, 6.3, 5.8, 7.1, 6.3,
6.5, 7.6, 4.9, 7.3, 6.7, 7.2, 6.5, 6.4, 6.8, 5.7, 5.8, 6.4, 6.5,
7.7, 7.7, 6. , 6.9, 5.6, 7.7, 6.3, 6.7, 7.2, 6.2, 6.1, 6.4, 7.2,
7.4, 7.9, 6.4, 6.3, 6.1, 7.7, 6.3, 6.4, 6. , 6.9, 6.7, 6.9, 5.8,
6.8, 6.7, 6.7, 6.3, 6.5, 6.2, 5.9],
[1.4, 1.4, 1.3, 1.5, 1.4, 1.7, 1.4, 1.5, 1.4, 1.5, 1.5, 1.6, 1.4,
1.1, 1.2, 1.5, 1.3, 1.4, 1.7, 1.5, 1.7, 1.5, 1. , 1.7, 1.9, 1.6,
1.6, 1.5, 1.4, 1.6, 1.6, 1.5, 1.5, 1.4, 1.5, 1.2, 1.3, 1.4, 1.3,
1.5, 1.3, 1.3, 1.3, 1.6, 1.9, 1.4, 1.6, 1.4, 1.5, 1.4, 4.7, 4.5,
4.9, 4. , 4.6, 4.5, 4.7, 3.3, 4.6, 3.9, 3.5, 4.2, 4. , 4.7, 3.6,
4.4, 4.5, 4.1, 4.5, 3.9, 4.8, 4. , 4.9, 4.7, 4.3, 4.4, 4.8, 5. ,
4.5, 3.5, 3.8, 3.7, 3.9, 5.1, 4.5, 4.5, 4.7, 4.4, 4.1, 4. , 4.4,
4.6, 4. , 3.3, 4.2, 4.2, 4.2, 4.3, 3. , 4.1, 6. , 5.1, 5.9, 5.6,
5.8, 6.6, 4.5, 6.3, 5.8, 6.1, 5.1, 5.3, 5.5, 5. , 5.1, 5.3, 5.5,
6.7, 6.9, 5. , 5.7, 4.9, 6.7, 4.9, 5.7, 6. , 4.8, 4.9, 5.6, 5.8,
6.1, 6.4, 5.6, 5.1, 5.6, 6.1, 5.6, 5.5, 4.8, 5.4, 5.6, 5.1, 5.1,
5.9, 5.7, 5.2, 5. , 5.2, 5.4, 5.1]])Anschließend transponieren wir das ganze zurück:
iris_x = features.T
iris_x[:5] # Testausgabearray([[5.1, 1.4],
[4.9, 1.4],
[4.7, 1.3],
[4.6, 1.5],
[5. , 1.4]])Daten auf zwei Klassen beschränken (binäre Klassifikation)
Wir beschränken uns auf die ersten 100 Vektoren, da wir nur 2 der 3 Klassen betrachten (jeweils 50 Daten pro Klasse).
iris_x = iris_x[:100] # nur die ersten 100 ElementeJetzt beschränken wir noch die Klassen auf die ersten 100 Daten. Zufälligerweise sind die Label der ja genau 0 und 1, so dass wir die Labelwerte nicht weiter anpassen müssen.
iris_y = iris.target[:100]
iris_yarray([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])Visualisierung der Daten
Da wir nur zwei Features haben, können wir diese auf x- und y-Achse abbilden und für die zwei Klassen eine jeweils andere Farbe wählen.
plt.scatter(features[0][:50], features[1][:50], color='red', marker='o', label='setosa')
plt.scatter(features[0][50:], features[1][50:], color='blue', marker='x', label='versicolor')
plt.xlabel('sepal length')
plt.ylabel('petal length')
plt.legend(loc='upper left')
plt.show()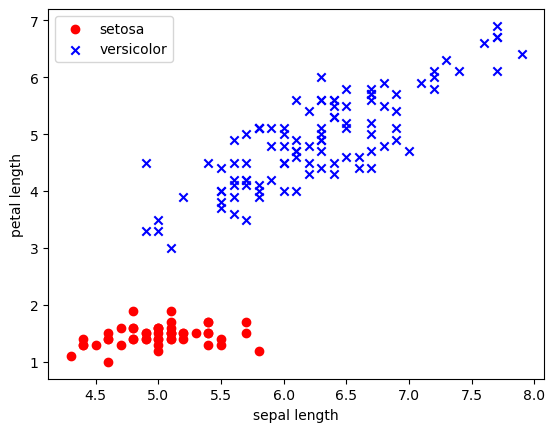
Wir sehen, dass die Daten sehr schön “linear separierbar” sind, d.h. man kann die zwei Klassen durch eine Gerade trennen.
Die Daten müssen später als NumPy-Arrays vorliegen:
iris_x = np.array(iris_x)
iris_y = np.array(iris_y)3.4.2 Klasse Perceptron
Wir definieren zunächst die Klasse Perceptron. Schauen Sie gern nochmal in Abschnitt 1.1.4, wenn Sie bestimmte Numpy-Konstrukte nicht verstehen (auch np.where ist dort erläutert).
class Perceptron():
# Konstruktor mit Defaultwerten
def __init__(self, alpha=0.01):
self.alpha = alpha
# Training mit x (Matrix von Featurevektoren) und y (Labels)
def fit(self, x, y, epochs=5):
ran = np.random.RandomState(42)
n_samples = x.shape[0]
print(f"Train on {n_samples} samples")
# Gewichte: 1 + dim(x) für den Bias
self.w = ran.normal(loc=0, scale=0.01, size=1 + x.shape[1])
# Speicher für Verlustfunktion (loss function) pro Epoche
self.loss = []
# Epochen durchlaufen
for i in range(epochs):
z = self.net_input(x) # Rohinput für alle Trainingsdaten
y_hat = self.activation(z) # Aktivierung für alle Trainingsdaten
diff = y - y_hat # Fehlervektor für alle Trainingsdaten
# Update der Gewichte
self.w[1:] += self.alpha * x.T.dot(diff)
# Update des Gewichts für das Bias-Neuron
self.w[0] += self.alpha * diff.sum()
# Kosten für diese Epoche (SSE) berechnen und in Liste speichern
l = (diff**2).sum() / 2.0
self.loss.append(l)
print(f"Epoch {i+1}/{epochs} - loss: {l:.4f}")
return self
# Aktivierungsfunktion: Identität (linear)
def activation(self, z):
return z
def net_input(self, x):
return np.dot(x, self.w[1:]) + self.w[0]
def predict(self, x):
return np.where(self.net_input(x) >= 0, 1, 0)
Besonders interessant ist natürlich die Methode fit, wo das Training in folgender Schleife stattfindet:
for i in range(epochs):
z = self.net_input(x)
y_hat = self.activation(z)
diff = y - y_hat
self.w[1:] += self.alpha * x.T.dot(diff)
self.w[0] += self.alpha * diff.sum()Matrix für alle Trainingsdaten
Zu beachten ist hier, dass die Matrix \(X\) alle Featurevektoren der Trainingsdaten enthält. Dadurch erreichen wir ganz elegant die Batch-Verarbeitung im Training, d.h. alle Trainingsdaten werden durchlaufen, bevor wir ein Update an den Gewichten vornehmen.
Man kann sich das so vorstellen, dass alle Featurevektoren übereinander gestapelt sind und somit eine Nx3-Matrix \(X\) ergeben (siehe Abbildung). Man bedenke, dass die erste Spalte der Matrix \(X\) das Bias-Neuron \(x_0\) repräsentiert, also nur Einsen enthält. Bei der Matrixmultiplikation der Nx3-Eingabematrix \(X\) mit dem 3x1-Gewichtsvektor \(w\) erhalten wir einen Nx1-Ausgabevektor \(\hat{Y}\), der alle Ausgaben für alle Trainingsbeispiele enthält.
Die Berechnung der Roheingabe ist in (Z) definiert:
\[ z = w^T x = w_1 x_1 + \ldots + w_n x_n \]
Im Code wird das in net_input berechnet:
def net_input(self, x):
return np.dot(x, self.w[1:]) + self.w[0] Hinweis: Die Multiplikationsreihenfolge bei Formel vs. Code ist unterschiedlich. In der Formel wird \(x\) von rechts mit \(w^T\) multipliziert, während im Code \(x\) von links an \(w\) multipliziert wird. Dann muss man eigentlich schreiben \(x^T w\), damit das \(x\) ein Zeilenvektor ist und \(w\) der Spaltenvektor. Und wenn Sie die Beispiele unten ansehen, werden Sie merken, dass die x-Vektoren tatsächlich Zeilenvektoren sind. Beide Repräsentationen sind möglich. Die Implementation folgt dem Konzept \(x^T w\).
Jetzt sehen wir uns an einem Beispiel an, wie die Berechnung im Code durchgeführt wird. Die folgende Abbildung zeigt das schematisch. Die x-Vektoren sind “übereinander gestapelt”. Man beachte, dass es Zeilenvektoren sind, also streng genommen ist jedes \(x\) eigentlich \(x^T\).

Die Abbildung entspricht noch nicht ganz dem Code, denn im Code wird das Gewicht des Bias-Neurons anders verarbeitet. Das schauen wir uns im Folgenden an.
Alternative Behandlung des Bias-Neurons
Im Code ist das mit dem Bias-Neuron etwas anders realisiert. Wir gehen jetzt davon aus, dass \(X\) die Matrix der übereinandergestapelten Featurevektoren ohne die jeweilige 1 für das Biasneuron ist. Wir können uns die ersten 3 Featurevektoren der Irisdaten ansehen:
iris_x[:3]array([[5.1, 1.4],
[4.9, 1.4],
[4.7, 1.3]])Wir möchten keine neue Matrix bauen, wo die erste Spalte aus Einsen besteht. Stattdessen vollziehen wir eine Matrixmultiplikation mit unserer Nx2-Eingabematrix \(X\) und dem 2x1-Gewichtsvektor \(w\) (wir lassen das \(w_0\) für das Biasneuron raus). Wir bekommen einen Nx1-“Pseudoausgabevektor”. Hier fehlt an jeder Stelle noch das \(x_0 \cdot w_0 = w_0\), das wir noch addieren müssen.
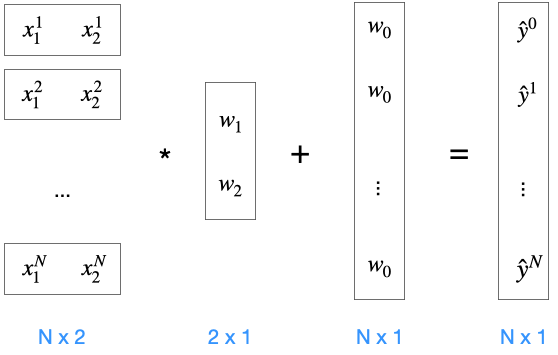
Für die Addition müssten wir eigentlich einen Vektor aus lauter \(w_0\) bauen, der so lang ist, wie es Trainingsbeispiele gibt. Stattdessen können wir komponentenweise Addition anwenden, ausgedrückt durch das Plus im Kreis. In Numpy geht das ganz leicht mit broadcasting.
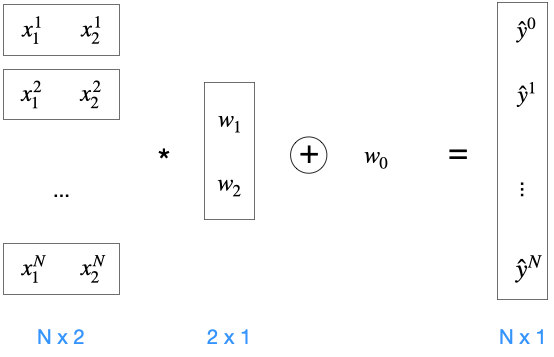
Das ist also gemeint mit
np.dot(x, self.w[1:]) + self.w[0] Gewichts-Updates
Kehren wir zurück zur Trainingsschleife:
z = self.net_input(x)
y_hat = self.activation(z)
diff = y - y_hat
self.w[1:] += self.alpha * x.T.dot(diff)
self.w[0] += self.alpha * diff.sum()Oben haben wir gesehen, dass in \(z\) alle Rohinputs stecken. Mit y_hat ist hier \(\hat{y} = g(z)\) gemeint. Dieser Vektor enthält alle berechneten Ausgaben für alle Trainingsbeispiele. Entsprechend enthält der Vektor diff alle Differenzen zwischen berechneter Ausgabe und echter Ausgabe.
Hier findet das Gewichtsupdate statt (ausgenommen das Bias-Neuron, das in der nächsten Zeile mit w[0] geupdatet wird), das auch den entsprechenden Gradienten beinhaltet.
self.w[1:] += self.alpha * x.T.dot(diff)Der Code folgt den Formeln (A 4) und (A 7), in denen das Update definiert wurde:
\[ w := w + \Delta w \]
\[ \Delta w_i = - \alpha \frac{\partial J}{\partial w_i} = \alpha \frac{1}{N} \sum_k \left( y^k - g(z^k) \right) x_i^k \]
Wenn wir das mit dem Code vergleichen, sollte also dieser Teil
x.T.dot(diff)dieser Formel entsprechen
\[ \sum_k \left( y^k - g(z^k) \right) x_i^k \]
Die Matrix \(X\) wird zunächst transponiert:
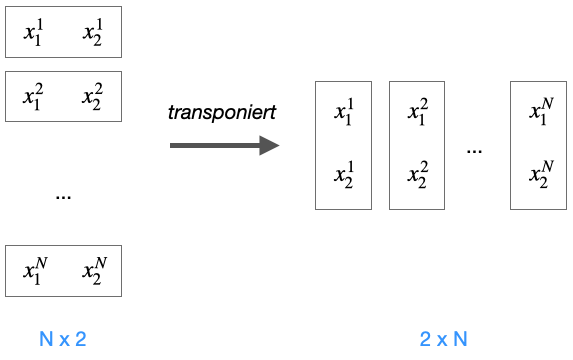
Anschließend wird \(X^T\) mit dem Vektor aller Differenzen über alle Trainingsbeispiele multipliziert:
x.T.dot(diff)Hier als Matrizen:
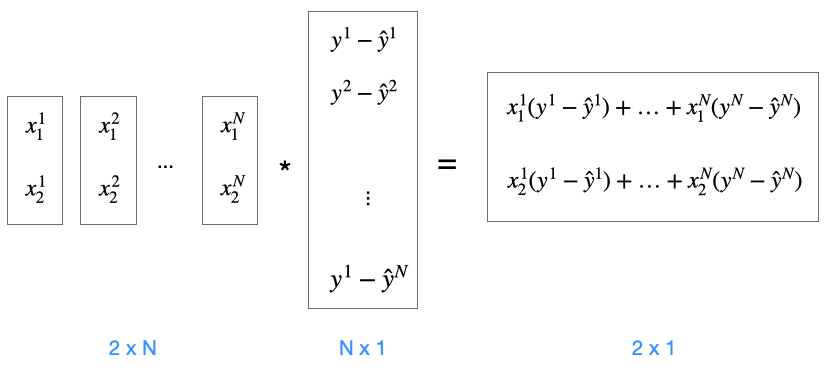
Die rechte Matrix enthält in Zeile 1 alle addierten Anpassungen für \(w_1\) für alle Trainingsbeispiele. Zeile 2 entsprechend für \(w_2\). Daher
self.w[1:] += self.alpha * x.T.dot(diff)Die Codezeile
self.w[0] += self.alpha * diff.sum()updatet das Bias-Neuron-Gewicht \(w_0\). Hier reicht es, die Differenzen zusammen zu addieren (Abb. oben, der mittlere Vektor), da ja alle \(x_i = 1\) sind.
3.4.3 Training mit zwei Lernraten
Jetzt, wo wir die Perceptron-Klasse verstanden haben, wenden wir uns dem konkreten Einsatz zu. Wir trainieren zwei Perzeptron-Netze, eines mit Lernrate 0.01, eines mit Lernrate 0.0001. Die Entwicklung der Kostenfunktion wird dabei in den jeweiligen Objekten mitprotokolliert (Instanzvariable loss).
EPOCHS = 20Training mit Lernrate 0.01
Die Lernrate wird beim Erstellen der Klasse mitgegeben.
model1 = Perceptron(alpha=0.01)
model1.fit(iris_x, iris_y, epochs=EPOCHS)Train on 100 samples
Epoch 1/20 - loss: 23.7989
Epoch 2/20 - loss: 24334.9132
Epoch 3/20 - loss: 37957919.7157
Epoch 4/20 - loss: 59208969090.5766
Epoch 5/20 - loss: 92357592414365.8594
Epoch 6/20 - loss: 144064742347031200.0000
Epoch 7/20 - loss: 224720561081757958144.0000
Epoch 8/20 - loss: 350532196498533588664320.0000
Epoch 9/20 - loss: 546780500149173669010079744.0000
Epoch 10/20 - loss: 852900014120760577106351489024.0000
Epoch 11/20 - loss: 1330403029897247964531781365923840.0000
Epoch 12/20 - loss: 2075239996079037720535038940854353920.0000
Epoch 13/20 - loss: 3237080000981913939835227627413569536000.0000
Epoch 14/20 - loss: 5049385590368112287706191504279880492646400.0000
Epoch 15/20 - loss: 7876325216702475760091903151316391867944271872.0000
Epoch 16/20 - loss: 12285950005006588998342183226694253397848432312320.0000
Epoch 17/20 - loss: 19164339126757914840331203369558938099531433098870784.0000
Epoch 18/20 - loss: 29893650390545246871046127287161095178251919536785719296.0000
Epoch 19/20 - loss: 46629853905289572200217874598033507686980745771985403904000.0000
Epoch 20/20 - loss: 72735957195657475175019364582358249508301312339071839319883776.0000<__main__.Perceptron at 0x7f8ec9b81d90>Was man hier sieht ist, dass der Fehler immer mehr ansteigt.
Training mit Lernrate 0.0001
Wir probieren es mit einer deutlich niedrigeren Lernrate.
model2 = Perceptron(alpha=0.0001)
model2.fit(iris_x, iris_y, epochs=EPOCHS)Train on 100 samples
Epoch 1/20 - loss: 23.7989
Epoch 2/20 - loss: 13.5561
Epoch 3/20 - loss: 9.8254
Epoch 4/20 - loss: 8.4030
Epoch 5/20 - loss: 7.8000
Epoch 6/20 - loss: 7.4894
Epoch 7/20 - loss: 7.2845
Epoch 8/20 - loss: 7.1190
Epoch 9/20 - loss: 6.9696
Epoch 10/20 - loss: 6.8278
Epoch 11/20 - loss: 6.6907
Epoch 12/20 - loss: 6.5571
Epoch 13/20 - loss: 6.4267
Epoch 14/20 - loss: 6.2992
Epoch 15/20 - loss: 6.1746
Epoch 16/20 - loss: 6.0526
Epoch 17/20 - loss: 5.9334
Epoch 18/20 - loss: 5.8168
Epoch 19/20 - loss: 5.7027
Epoch 20/20 - loss: 5.5911<__main__.Perceptron at 0x7f8ec9b813a0>Der Fehler wird offenbar geringer.
3.4.4 Visualisierung
Wir zeichnen den Verlauf der Kostenfunktion über die Epochen. Das erste Netz mit Lernrate 0.01 hat steigende Kosten, d.h. das Netz wird schlechter. Das zweite Netz mit Lernrate 0.0001 zeigt dagegen sinkende Kosten.
Wir verwenden eine logarithmische Darstellung der Werte (log10), damit der Verlauf darstellbar bleibt.
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(10,4))
ax[0].plot(range(1, len(model1.loss)+1), np.log10(model1.loss), marker='o')
ax[0].set_xlabel('Epochen')
ax[0].set_ylabel('log(SSE)')
ax[0].set_title('Perceptron, alpha=0.01')
ax[1].plot(range(1, len(model2.loss)+1), np.log10(model2.loss), marker='o')
ax[1].set_xlabel('Epochen')
ax[1].set_ylabel('log(SSE)')
ax[1].set_title('Perceptron, alpha=0.0001')
plt.show()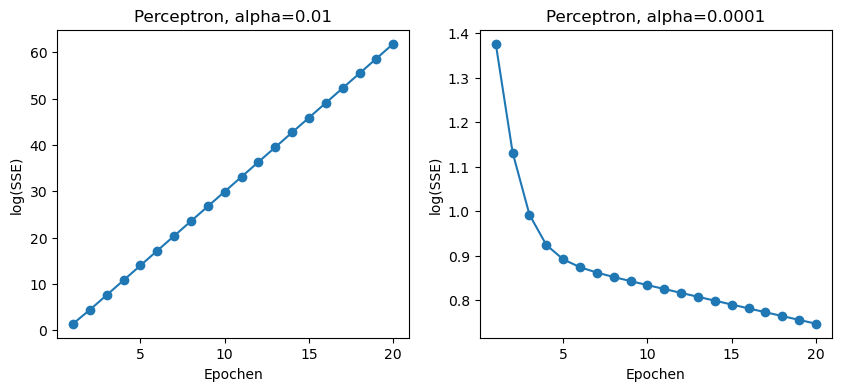
Probleme
In den obigen Graphen sehen wir zwei Probleme:
- Bei einer Lernrate von \(0.01\) scheint das Netz ständig über das Minimum hinauszuschießen (Overshoot) und entfernt sich sogar davon, so dass der Gesamtfehler sich im Training sogar immer weiter erhöht.
- Bei einer kleineren Lernrate von \(0.0001\) reduziert sich der Gesamtfehler, aber aufgrund der kleinen Lernrate könnte es viele Epochen dauern, bevor das echte Minimum erreicht ist.
3.5 Feature-Scaling
Bei unserer Python-Implememtierung mussten wir eine sehr niedrige Lernrate wählen, um das Lernen zu ermöglichen, was wiederum das Training verlangsamt. Die Ursache für die niedrige Lernrate könnte die stark unterschiedliche Skalierung der Features sein. Es kann ein Problem sein, wenn ein Feature sich im Bereich 1000-2000 bewegt und ein anderes Feature im Bereich 0.001 bis 0.0015. Das erschwert den Gradientenabstieg, wie Abbildung 3.4 illustriert. Man sieht die Gewichte als 2D-Darstellung. Der Fehler wird hier mit “Höhenlinien” dargestellt. Der Gradientenabstieg vollzieht sich mit sehr langgestreckten Vektoren, was es erschwert, das Verfahren über eine einheitliche Lernrate zu kontrollieren. Im Zweifelsfall muss die Lernrate sehr niedrig ausfallen.
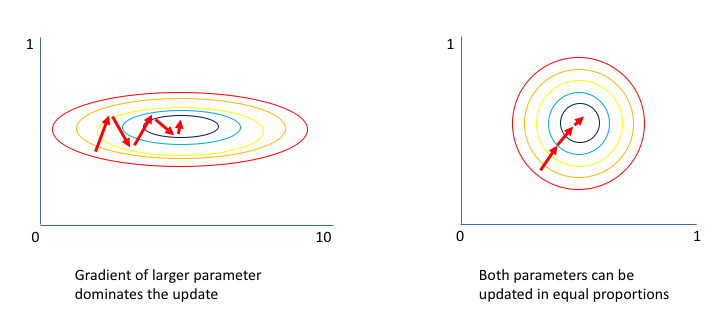
Eine Maßnahme, die Abhilfe schafft, ist das Anpassen der Features, so dass sich die Features in einem ähnlichen Wertebereich bewegen. Es gibt zwei Arten der Skalierung: Normalisieren und Standadisieren.
Normalisieren
Beim Normalisieren skaliert man alle Features auf den Bereich \([0, 1]\). Bei Featurevektoren \(x^k\) berechnet man die normalisierten Vektoren \(\bar{x}^k\) für jedes einzelne Feature \(i\) einzeln:
\[ \bar{x}_i^k = \frac{x_i^k - min_i}{max_i - min_i} \]
Hier stehen \(min_i\) und \(max_i\) für das Minimum/Maximum eines Features \(i\) über alle Vektoren \(x^k\).
Wenn die ursprünglichen Werte bei 0 beginnen (d.h. \(min_i = 0\)), was gar nicht so selten der Fall ist, ist diese Umformung natürlich extrem leicht:
\[ \bar{x}_i^k = \frac{x_i^k}{max_i} \]
Typisches Beispiel aus der Bildverarbeitung: Bei einem Schwarzweiß-Bild liegen die Pixel in der Regel als Grauwert im Bereich \(\{0, \ldots, 255\}\) vor. Bei einem Farbbild sind es drei Werte, einen pro Farbkanal (Rot, Gelb, Blau).
Bleiben wir beim Schwarzweiß-Bild. Wenn wir einen NumPy-Array haben:
data = np.array([13, 120, 5, 211])
dataarray([ 13, 120, 5, 211])Können wir ausnutzen, dass NumPy die komponentenweise Anwendung von mathematischen Operationen mit dieser eleganten Formulierung erlaubt:
data = data/255
dataarray([0.05098039, 0.47058824, 0.01960784, 0.82745098])Achten Sie darauf, dass ein “data/255” allein (ohne das “data =”) nicht ausreicht, weil in dem Fall das Array nicht verändert wird.
Standardisieren
Beim Standardisieren will man erreichen, dass die Featurewerte sich gemäß einer Normalverteilung verhalten, mit Mittelwert \(0\) und einer Standardabweichung von \(1\). Dazu muss man für ein Feature \(i\) den Mittelwert \(\mu_i\) und die Standardabweichung \(\sigma_i\) berechnen. Dann verschiebt und skaliert man jedes Feature wie folgt:
\[ \bar{x}_i^k = \frac{x_i^k - \mu_i}{\sigma_i} \]
Auch hier ein Praxisbeispiel: In NumPy lässt sich beides leicht realisieren, da es Funktionen wie mean (Mittelwert) und std (Standardabweichung) gibt, die man einfach auf NumPy-Arrays anwenden kann.
iris_x_st = np.copy(iris_x)
iris_x_st[:3]array([[5.1, 1.4],
[4.9, 1.4],
[4.7, 1.3]])Wir müssen darauf achten, dass wir jedes der beiden Feature getrennt behandeln. Das Feature wird über den zweiten Index gesteuert.
iris_x[:10,0]array([5.1, 4.9, 4.7, 4.6, 5. , 5.4, 4.6, 5. , 4.4, 4.9])Wir standardisieren das erste Feature:
iris_x_st[:, 0] = (iris_x[:,0] - iris_x[:,0].mean()) / iris_x[:,0].std()
iris_x_st[:3]array([[-0.5810659 , 1.4 ],
[-0.89430898, 1.4 ],
[-1.20755205, 1.3 ]])Und jetzt das zweite Feature:
iris_x_st[:, 1] = (iris_x[:,1] - iris_x[:,1].mean()) / iris_x[:,1].std()
iris_x_st[:3]array([[-0.5810659 , -1.01297765],
[-0.89430898, -1.01297765],
[-1.20755205, -1.08231219]])Trainieren mit standardisierten Daten
Wir greifen unsere Python-Implementierung aus Abschnit 3.4.3 wieder auf und erstellen ein drittes Netz. Wir trainieren es jetzt mit den standardisierten Daten und Lernrate 0.01.
model3 = Perceptron(alpha=0.01)
model3.fit(iris_x_st, iris_y, epochs=EPOCHS)Train on 100 samples
Epoch 1/20 - loss: 24.4906
Epoch 2/20 - loss: 8.2845
Epoch 3/20 - loss: 5.6750
Epoch 4/20 - loss: 3.9525
Epoch 5/20 - loss: 2.8155
Epoch 6/20 - loss: 2.0650
Epoch 7/20 - loss: 1.5696
Epoch 8/20 - loss: 1.2426
Epoch 9/20 - loss: 1.0267
Epoch 10/20 - loss: 0.8842
Epoch 11/20 - loss: 0.7902
Epoch 12/20 - loss: 0.7281
Epoch 13/20 - loss: 0.6871
Epoch 14/20 - loss: 0.6601
Epoch 15/20 - loss: 0.6422
Epoch 16/20 - loss: 0.6304
Epoch 17/20 - loss: 0.6227
Epoch 18/20 - loss: 0.6175
Epoch 19/20 - loss: 0.6141
Epoch 20/20 - loss: 0.6119<__main__.Perceptron at 0x7f8ea917ebb0>Wir sehen uns die Kostenentwicklung im direkten Vergleich mit dem zweiten Netz an. Wir können jetzt den Logarithmus weglassen, weil keine extrem hohen Werte vorkommen.
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(10,4))
ax[0].plot(range(1, len(model2.loss)+1), model2.loss, marker='o')
ax[0].set_xlabel('Epochen')
ax[0].set_ylabel('SSE')
ax[0].grid()
ax[0].set_ylim([0, 25]) # gleiche y-Skala anlegen
ax[0].set_title('Perceptron, alpha=0.0001')
ax[1].plot(range(1, len(model3.loss)+1), model3.loss, marker='o')
ax[1].set_xlabel('Epochen')
ax[1].set_ylabel('SSE')
ax[1].grid()
ax[0].set_ylim([0, 25]) # gleiche y-Skala anlegen
ax[1].set_title('Perceptron standardisiert, alpha=0.01')
plt.show()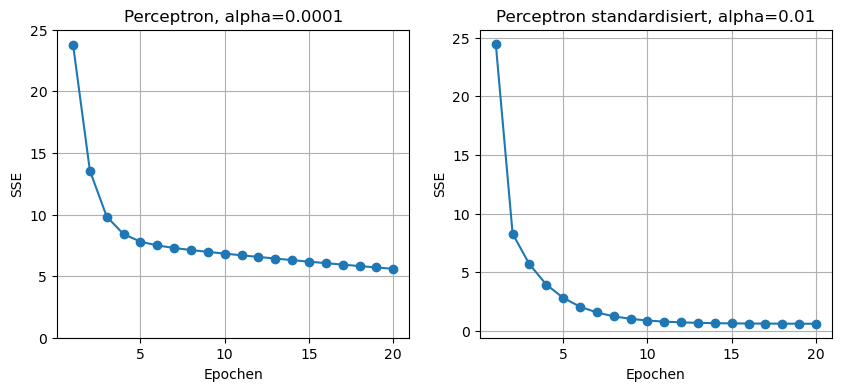
Man sieht klar, dass das Netz mit den standardisierten Daten (rechts) schneller lernt, auch weil die Lernrate mit \(0.01\) deutlich höher ist.
Zur Erinnerung: Auf den nicht-standardisierten Daten hat eine Lernrate von \(0.01\) dazu geführt, dass der Fehler sich ständig vergrößert (siehe oben).
3.6 Stochastic Gradient Descent (SGD) und Minibatch
Oben sind wir davon ausgegangen, dass wir erst alle Trainingsbeispiele abarbeiten, die Deltas für jedes Einzelgewicht aufsummieren, und am Ende die Gewichte anpassen. Das kann dazu führen, dass das System sehr langsam lernt, da sich wichtige Gewichtsänderungen am Ende einer Epoche “rausmitteln”. Man nennt diese Vorgehensweise manchmal Batch-Learning, aber dieser Begriff ist missverständlich, weil man auch manchmal Minibatch-Learning damit meint. In der Praxis kommt es kaum noch vor, dass alle Trainingsbeispiele vor dem Update der Gewichte durchlaufen werden.
Beim Perzeptron haben wir die Gewichte nach jedem einzelnen Sample angepasst, das ist im Grunde eine Form von SGD.
3.6.1 Stochastic Gradient Descent (SGD)
SGD bedeutet, dass man die Gewichte nach jedem einzelnen Trainingsbeispiel anpasst. Das nennt man manchmal auch Online-Learning. Der Begriff “Online” bezieht sich auf Szenarien, wo sich eine System “live” im Einsatz befindet und auf jede neue Einzelinformation (z.B. aus der Umwelt) eine Anpassung vornimmt. Da die Samples bei dieser Methode zufällig ausgewählt werden (anstatt in immer dergleichen Reihenfolge), spricht man von Stochastic Gradient Descent.
Der Nachteil dieser Methode ist, dass mehr Rechenleistung zum Einsatz kommt. Bei 60000 Trainingsbeispielen wird pro Epoche nicht ein einziges Update durchgeführt, sondern es werden 60000 Updates durchgeführt. Technisch führt dies dazu, dass man nicht mehrere Trainingsbeispiele zu einer Matrix \(X\) zusammenfassen kann, wie oben skizziert, und die damit einhergehenden Performancevorteile nicht zum Zuge kommen.
Darüber hinaus schanken die Gewichte stark, da jedes Trainingsbeispiel (auch z.B. “schlechte” Beispiele) direkt die Gewichte beeinflussen. Schlechte Einflüsse werden also nicht “herausgemittelt”. Also muss man eher eine sehr niedrige Lernrate wählen, was wiederum das Training verlangsamt.
3.6.2 Minibatch
Anstatt die Gewichte entweder nach jedem Beispiel zu updaten oder erst nach Durchlaufen aller Beispiele, kann man eine Teilmenge der Trainingsbeispiele durchlaufen, bevor ein Update durchgeführt wird. Für große Datensätze ist das die Methode der Wahl. Diese Teilmengen nennt man auch Batches und bei Bibliotheken gibt man häufig die Größe dieser Batches an (batch size), z.B. 32 oder 64.
Die Trainingsdaten werden also in Batches aufgeteilt. In einer Epoche werden alle Batches durchlaufen.
Wir werden Minibatch im nächsten Kapitel beim Thema “Backpropagation” im Aktion sehen.
Siehe auch die Videos von Andrew Ng: Mini Batch Gradient Descent und Understanding Mini-Batch Gradient Descent
3.6.3 SGD in Keras = Minibatch
SGD nennt man in Keras auch Optimierungsmethode, da es noch einige Varianten gibt (z.B. Adam oder RMSprop). In Keras wird im Grunde immer Minibatch durchgeführt, es sei denn, man zwingt Keras dazu, nach jedem einzelnen Trainingsbeispiel ein Update durchzuführen.
Sie sehen dies daran, dass die Methode fit einen Parameter batch_size anbieten, der per Default auf 32 eingestellt ist. Dies ist genau die Batchgröße in Minibatch.