import torch
import torch.nn as nn
import torch.nn.functional as FAnhang F: PyTorch - Neuronale Netze
In diesem Kapitel konzentrieren wir uns auf Neuronale Netze in PyTorch, also wie sie erzeugt, konfiguriert und trainiert werden. Wir sehen außerdem, wie man die in PyTorch mitgelieferten Datensätze (z.B. FashionMNIST) nutzt. Zum Schluss sehen wir uns kurz ein äquivalenten Netz in Keras an, damit man innerhalb des Kapitels den direkten Vergleich ziehen kann.
Wichtige Ressourcen zum Thema:
Importe
F.1 Neuronale Netze
In PyTorch muss man für jedes Netz eine eigene Klasse anlegen. Für das Training programmiert man die Schleife über alle Epochen selbst. Was anfangs - besonders im Vergleich zu Keras - etwas sperrig scheint, erlaubt später eine mehr Kontrolle und regt mehr zum Experimentieren an.
Wir beginnen mit der Definition von zwei Beispielnetzen, einem Feedforwad-Netz (FNN, Kapitel 4) und einem Konvolutionsnetz (CNN, Kapitel 10). Als Daten wählen wir FashinMNIST (Abschnit 9.3.1).
F.1.1 Feedforward-Netz
In PyTorch definiert man ein neues Netz als Unterklasse von nn.Module.
Die Klasse nn.Linear wiederum repräsentiert eine traditionelle Schicht, die wir auch fully connected nennen. In Keras entspricht das einem “Dense Layer”.
Wir erstellen hier ein Feedforward-Netz mit 784 Eingabeneuronen, 200 Zwischenneuronen und 10 Ausgabeneuronen. Als Aktivierungsfunktion wählen wir ReLU.
Siehe auch torch.nn.Module, torch.nn.Linear
Funktionale Schreibweise
In der funktionalen Schreibweise, erzeugen wir im Konstruktor Objekte für alle Schichten und rufen in der Methode forward die Schichten auf und schicken den Output gegebenfalls noch durch Funktionen wie ReLU.
class SimpleNet0(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.fc1 = nn.Linear(784, 200)
self.fc2 = nn.Linear(200, 10)
def forward(self, x):
x = self.flatten(x)
x = self.fc1(x)
x = F.relu(x)
return x
fnn0 = SimpleNet0()
print(fnn0)SimpleNet0(
(flatten): Flatten(start_dim=1, end_dim=-1)
(fc1): Linear(in_features=784, out_features=200, bias=True)
(fc2): Linear(in_features=200, out_features=10, bias=True)
)Sanity Check: Das Netz erwartet einen 4-dimensionalen Tensor der Form
(Batches, Kanäle, Zeilen, Spalten)Als Test schicken eine zufällige 28x28-Matrix durch das Netz.
data = torch.rand((1, 1, 28, 28))
result = fnn0(data)
print (result)tensor([[0.0150, 0.7567, 0.0000, 0.0469, 0.0793, 0.0000, 0.1568, 0.0000, 0.0000,
0.1371, 0.0000, 0.7556, 0.1179, 0.5842, 0.0000, 0.0000, 0.0000, 0.4385,
0.2659, 0.2603, 0.2856, 0.5434, 0.4088, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.3644, 0.0000, 0.3550, 0.3717, 0.0000,
0.0000, 0.0000, 0.7984, 0.0000, 0.0000, 0.1369, 0.3563, 0.2242, 0.0115,
0.0000, 0.0000, 0.1070, 0.0000, 0.5718, 0.0000, 0.0039, 0.0000, 0.0000,
0.0000, 0.0032, 0.0000, 0.0000, 0.1076, 0.1135, 0.0000, 0.0000, 0.0000,
0.0000, 0.2357, 0.0000, 0.1021, 0.6461, 0.0000, 0.0000, 0.6423, 0.0000,
0.3891, 0.1391, 0.0000, 0.0000, 0.4445, 0.7454, 0.0550, 0.0000, 0.1914,
0.0463, 0.0000, 0.1768, 0.0261, 0.0000, 0.0000, 0.0000, 0.0000, 0.4852,
0.0000, 0.4501, 0.0000, 0.2233, 0.0000, 0.0000, 0.0000, 0.1611, 0.0000,
0.2169, 0.0000, 0.5235, 0.1648, 0.2173, 0.2701, 0.2702, 0.7856, 0.0000,
0.3020, 0.2922, 0.0000, 0.0849, 0.0401, 0.1780, 0.4016, 0.3670, 0.0000,
0.3896, 0.0000, 0.0000, 0.0518, 0.0000, 0.0000, 0.0000, 0.0000, 0.6390,
0.4434, 0.4178, 0.1412, 0.1089, 0.3659, 0.0000, 0.0000, 0.0000, 0.2039,
0.5875, 0.1878, 0.0000, 0.0179, 0.0164, 0.4019, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.5311, 0.0000, 0.0000, 0.1313, 0.6662, 0.5792, 0.0000,
0.2590, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.3199, 0.1822, 0.4481,
0.0000, 0.2875, 0.0000, 0.3373, 0.3991, 0.0000, 0.0699, 0.0000, 0.0000,
0.0000, 0.1538, 0.3532, 0.0000, 0.0000, 0.0000, 0.0000, 0.3218, 0.2692,
0.0000, 0.0000, 0.2264, 0.6294, 0.0000, 0.4354, 0.1495, 0.3324, 0.0000,
0.0000, 0.0251, 0.0000, 0.0396, 0.7478, 0.0000, 0.0989, 0.2476, 0.2275,
0.2645, 0.3112]], grad_fn=<ReluBackward0>)Wir sehen uns die Parameter der ersten Schicht an. Es handelt sich um eine 200x784-Matrix mit den Gewichten von den 784 Eingabeneuronen zu den 200 Neuronen der Zwischenschicht.
for p in fnn0.parameters():
print(p.shape)
print(p)
breaktorch.Size([200, 784])
Parameter containing:
tensor([[-0.0192, 0.0327, -0.0075, ..., -0.0315, -0.0106, -0.0289],
[ 0.0184, -0.0264, 0.0311, ..., 0.0229, -0.0011, -0.0011],
[ 0.0043, 0.0043, -0.0318, ..., 0.0158, 0.0197, -0.0119],
...,
[ 0.0244, -0.0269, 0.0014, ..., 0.0330, -0.0258, -0.0014],
[-0.0039, 0.0213, -0.0083, ..., -0.0090, 0.0023, 0.0251],
[-0.0005, 0.0319, -0.0319, ..., -0.0189, 0.0265, -0.0339]],
requires_grad=True)Kompakte Schreibweise
Mit einem Objekt vom Typ Sequential kann man die Schichten und die Verarbeitung etwas kompakter schreiben. Die Schreibung erinnert an die Schreibweise in Keras.
class SimpleNet(nn.Module):
def __init__(self):
super().__init__()
# Definiere Schichten und Aktivierungsfunktion
self.layers = nn.Sequential(
nn.Flatten(),
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10)
)
def forward(self, x):
return self.layers(x) # Hier werden alle Schichten durchlaufen
fnn = SimpleNet()
print(fnn)SimpleNet(
(layers): Sequential(
(0): Flatten(start_dim=1, end_dim=-1)
(1): Linear(in_features=784, out_features=200, bias=True)
(2): ReLU()
(3): Linear(in_features=200, out_features=10, bias=True)
)
)Wieder ein Datencheck:
data = torch.rand((1, 1, 28, 28))
result = fnn(data)
print (result)tensor([[ 0.0137, 0.0528, -0.3200, -0.1228, -0.1057, -0.0945, 0.0229, 0.0786,
-0.0895, -0.1267]], grad_fn=<AddmmBackward0>)F.1.2 Konvolutionsnetze
Als nächstes erstellen wir ein Konvolutionsnetz mit Hilfe der Klassen Conv2d und MaxPool2d.
Conv2dhat die Parameter (Anzahl der Eingabekanäle, Anzahl der Filter, Kernelgröße)- per Default sind Stride=1 und Padding=0 eingestellt
MaxPool2dhat die Parameter (Kernelgröße, Stride)
Bei der Konv-Schicht gilt: Anzahl der Filter = Anzahl der Kanäle der Ausgabe.
Im Beispielnetz haben wir folgende Schichten:
- Inputschicht: (28x28x1)
- Konv-Schicht: 6 Filter der Größe 5x5x1, Output (24x24x6)
- Pooling-Schicht: Größe 2x2, Stride 2, Output (12x12x6)
- Konv-Schicht: 16 Filter der Größe 5x5x6, Output (8x8x16)
- Pooling-Schicht: Größe 2x2, Stride 2, Output (4x4x6)
- FC-Schicht: 80 Neuronen
- FC-Ausgabeschicht: 10 Neuronen
Siehe auch torch.nn.Conv2d, torch.nn.MaxPool2d
Funktionale Schreibweise
In der funktionalen Schreibweise kann die Verarbeitung in forward etwas unübersichtlich werden.
class ConvNet0(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 4 * 4, 80)
self.fc2 = nn.Linear(80, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = torch.flatten(x, 1)
x = F.relu(self.fc1(x))
x = self.fc2(x)
return x
cnn0 = ConvNet0()
print(cnn0)ConvNet0(
(conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
(pool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
(fc1): Linear(in_features=256, out_features=80, bias=True)
(fc2): Linear(in_features=80, out_features=10, bias=True)
)Sanity check:
data = torch.rand((1, 1, 28, 28))
result = cnn0(data)
print (result)tensor([[-0.0848, -0.0865, 0.0776, 0.0613, -0.0174, -0.0524, -0.0037, -0.1327,
-0.0463, 0.1279]], grad_fn=<AddmmBackward0>)Kompakte Schreibweise
Die kompakte Schreibweise mit Sequential ist deutlich lesbarer als die funktionale Schreibweise.
class ConvNet(nn.Module):
def __init__(self):
super().__init__()
self.layers = nn.Sequential(
nn.Conv2d(1, 6, kernel_size = 5),
nn.ReLU(),
nn.MaxPool2d(2, 2),
nn.Conv2d(6, 16, kernel_size = 5),
nn.ReLU(),
nn.Flatten(),
nn.Linear(16 * 8 * 8, 80),
nn.ReLU(),
nn.Linear(80, 10)
)
def forward(self, x):
return self.layers(x)
cnn = ConvNet()
print(cnn)ConvNet(
(layers): Sequential(
(0): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
(1): ReLU()
(2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(3): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
(4): ReLU()
(5): Flatten(start_dim=1, end_dim=-1)
(6): Linear(in_features=1024, out_features=80, bias=True)
(7): ReLU()
(8): Linear(in_features=80, out_features=10, bias=True)
)
)Auch hier ein kurzer Sanity check.
data = torch.rand((1, 1, 28, 28))
result = cnn(data)
print (result)tensor([[-0.0402, -0.1419, -0.1471, -0.0653, -0.0747, 0.1125, 0.1374, -0.0110,
0.0211, -0.1175]], grad_fn=<AddmmBackward0>)F.2 Daten
Als Datensatz nehmen wir FashionMNIST, also Graustufen-Bilder von Kleidungsstücken (Abschnitt 9.3.1).
Zum Akquirieren von Daten benötigen wir das Paket torchvision. Das darin vorkommende “vision” kommt von “computer vision”, d.h. es geht um Operationen im Bereich Bildverarbeitung.
Schauen Sie sich unbedingt an, welche Datensätze in PyTorch enthalten sind und in welcher Form sie vorliegen: PyTorch Datasets
Wir benötigen die folgenden Imports:
from torchvision import datasets
from torchvision.transforms import ToTensorF.2.1 Daten laden
Die folgenden Zeilen laden die Daten herunter (es sei denn, sie sind bereits vorhanden) und legen sie im Unterverzeichnis “data” ab. In unserem Fall wird das Verzeichnis “data/FashionMNIST” angelegt und dort die Daten hineingeschrieben.
Die Daten sind Bilddaten (PIL image, PIL = python image library) und müssen explizit mit dem “transform”-Argument in PyTorch-Tensoren umgewandelt werden.
training_data = datasets.FashionMNIST(
root="data",
train=True,
download=True,
transform=ToTensor(),
)
test_data = datasets.FashionMNIST(
root="data",
train=False,
download=True,
transform=ToTensor(),
)F.2.2 DataLoader erzeugen
Ein Loader ist eine Datenstruktur, über die man iterieren kann, so dass man in einer For-Schleife jede Entität nacheinander abarbeitet.
from torch.utils.data import DataLoaderHier wird ein wichtiger Hyperparameter definiert:
- Batchgröße: Wieviele Trainingsbeispiele sollen durchlaufen werden, bevor die Gewichte angepasst werden.
batch_size = 64Wir geben eine Batchgröße von 64 an. Ein “Batch” ist ein Tensor, der - in unserem Fall - 64 Trainingsbeispiele mit jeweils Features und Zielwert enthält. Der Loader enthält entsprechend eine Liste von allen Batches.
train_dataloader = DataLoader(training_data, batch_size=batch_size)
test_dataloader = DataLoader(test_data, batch_size=batch_size)F.2.3 Daten inspizieren
Wir sehen uns die Dimensionen des jeweils ersten Tensors (X und y) in den Trainingsdaten an:
for X, y in train_dataloader:
print(f"X shape = {X.shape}")
print(f"y shape = {y.shape} {y.dtype}")
breakX shape = torch.Size([64, 1, 28, 28])
y shape = torch.Size([64]) torch.int64Auf der Feature-Seite \(X\) ist der erste Tensor ein Batch von 64 Tensoren der Form 1x28x28. Die “1” bezieht sich auf die Anzahl der Kanäle, bei einem Graustufenbild ist das nur einer.
Bei den Labels \(y\) haben wir 64 Integer-Werte.
Wenn wir “enumerate” benutzen, können wir eine Laufvariable für die Batchnummer mitführen. Das werden wir später noch verwenden.
for batch, (X, y) in enumerate(train_dataloader):
print(f"{batch}: X shape = {X.shape}")
print(f"{batch}: y shape = {y.shape} {y.dtype}")
break0: X shape = torch.Size([64, 1, 28, 28])
0: y shape = torch.Size([64]) torch.int64In dem \(X\) oben steckt noch den Tensor des ersten Batches. Mit X[0][0] bekommt das erste Bild und den ersten (und einzigen) Kanal und kann es mit imshow (image show) plotten.
import matplotlib.pyplot as plt
plt.imshow(X[0][0].view([28,28]))
plt.show()
Die dazugehörige Kategorie ist:
print(y[0].item())9F.3 Training
F.3.1 Hyperparameter
Zunächst definieren wir zwei weitere Hyperparameter:
- Anzahl der Epochen: Dauer des Trainings (eine Epoche = Durchlaufen aller Trainingsdaten).
- Lernrate: Wie stark sollen die Gewichte pro Update (nach jedem Batch) angepasst werden.
- Momentum: Parameter für eine adaptive Lernrate, welche den “Schwung” der vorherigen Anpassung mit berücksichtigt (wird fast immer auf 0.9 gesetzt)
epochs = 20
learning_rate = 0.01
momentum = 0.9Definition der Fehlerfunktion:
loss_func = nn.CrossEntropyLoss()Festlegen des Optimierungsverfahrens:
F.3.2 Trainings- und Testfunktion
Jetzt definieren wir das Trainingsprozedere:
def train(dataloader, model, loss_func, optimizer):
size = len(dataloader.dataset)
correct = 0
model.train()
# Durchlaufe alle Batches
for batch, (X, y) in enumerate(dataloader):
# Vorhersagen und Fehler berechnen
pred = model(X)
loss = loss_func(pred, y)
correct += (pred.argmax(1) == y).type(torch.float).sum().item()
# Backpropagation
optimizer.zero_grad() # Setzt die Gradienten auf Null
loss.backward() # Berechnet alle Gradienten
optimizer.step() # Führt Update auf den Gewichten durch
#if batch % 200 == 0:
# loss, current = loss.item(), batch * len(X)
# print(f"[{current:>5d}/{size:>5d}] Loss = {loss:>0.3f} ")
correct /= size
#print(f"\nTraining Acc = {(100*correct):>0.1f}%")
return loss.item(), 100*correct # return loss and accuracyEine separate Funktion für das Evaluieren des Modells auf den Testdaten.
def test(dataloader, model, loss_func):
size = len(dataloader.dataset)
num_batches = len(dataloader)
model.eval()
loss, correct = 0, 0
with torch.no_grad():
# Durchlaufe alle Batches
for X, y in dataloader:
# Vorhersagen und Fehler berechnen (und aufaddieren)
pred = model(X)
loss += loss_func(pred, y).item()
correct += (pred.argmax(1) == y).type(torch.float).sum().item()
# Durchschnitt bilden
loss /= num_batches
correct /= size
#print(f"Test Acc = {(100*correct):>0.1f}% (Loss = {loss:>0.3f})\n")
return loss, 100*correct # return loss and accuracyF.3.3 Training FNN
Wir trainieren unser einfaches Feedforward-Netz.
optimizer = torch.optim.SGD(fnn.parameters(), lr=learning_rate, momentum=momentum)history1 = {}
history1['acc'] = []
history1['loss'] = []
history1['val_acc'] = []
history1['val_loss'] = []
for e in range(epochs):
loss, acc = train(train_dataloader, fnn, loss_func, optimizer)
history1['acc'].append(acc)
history1['loss'].append(loss)
vloss, vacc = test(test_dataloader, fnn, loss_func)
history1['val_acc'].append(vacc)
history1['val_loss'].append(vloss)
print(f"Epoch {e+1:>2}: acc={acc:>0.1f} loss={loss:>0.4f} val_acc={vacc:>0.1f} val_loss={vloss:>0.4f}")
print("\nFinished")Epoch 1: acc=78.5 loss=0.5539 val_acc=82.8 val_loss=0.4877
Epoch 2: acc=84.6 loss=0.4106 val_acc=84.2 val_loss=0.4499
Epoch 3: acc=86.2 loss=0.3306 val_acc=84.4 val_loss=0.4387
Epoch 4: acc=87.0 loss=0.2972 val_acc=84.9 val_loss=0.4195
Epoch 5: acc=87.6 loss=0.2447 val_acc=85.4 val_loss=0.4040
Epoch 6: acc=88.1 loss=0.2395 val_acc=85.8 val_loss=0.3898
Epoch 7: acc=88.6 loss=0.2247 val_acc=86.0 val_loss=0.3851
Epoch 8: acc=89.0 loss=0.2287 val_acc=86.3 val_loss=0.3749
Epoch 9: acc=89.3 loss=0.2324 val_acc=86.7 val_loss=0.3681
Epoch 10: acc=89.6 loss=0.2091 val_acc=87.0 val_loss=0.3634
Epoch 11: acc=90.0 loss=0.2088 val_acc=87.1 val_loss=0.3639
Epoch 12: acc=90.3 loss=0.2046 val_acc=87.0 val_loss=0.3571
Epoch 13: acc=90.5 loss=0.1767 val_acc=87.4 val_loss=0.3529
Epoch 14: acc=90.8 loss=0.1736 val_acc=87.3 val_loss=0.3559
Epoch 15: acc=91.1 loss=0.1721 val_acc=87.5 val_loss=0.3501
Epoch 16: acc=91.3 loss=0.1766 val_acc=87.6 val_loss=0.3479
Epoch 17: acc=91.5 loss=0.1655 val_acc=87.3 val_loss=0.3491
Epoch 18: acc=91.7 loss=0.1628 val_acc=87.4 val_loss=0.3518
Epoch 19: acc=91.9 loss=0.1579 val_acc=87.5 val_loss=0.3492
Epoch 20: acc=92.1 loss=0.1392 val_acc=87.6 val_loss=0.3551
FinishedF.3.4 Training Konvolutionsnetz
optimizer = torch.optim.SGD(cnn.parameters(), lr=learning_rate, momentum=momentum)history2 = {}
history2['acc'] = []
history2['loss'] = []
history2['val_acc'] = []
history2['val_loss'] = []
for e in range(epochs):
loss, acc = train(train_dataloader, cnn, loss_func, optimizer)
history2['acc'].append(acc)
history2['loss'].append(loss)
vloss, vacc = test(test_dataloader, cnn, loss_func)
history2['val_acc'].append(vacc)
history2['val_loss'].append(vloss)
print(f"Epoch {e+1:>2}: acc={acc:>0.1f} loss={loss:>0.4f} val_acc={vacc:>0.1f} val_loss={vloss:>0.4f}")
print("Finished")Epoch 1: acc=75.5 loss=0.4404 val_acc=82.2 val_loss=0.4903
Epoch 2: acc=85.4 loss=0.3460 val_acc=84.7 val_loss=0.4214
Epoch 3: acc=87.3 loss=0.2996 val_acc=85.9 val_loss=0.3995
Epoch 4: acc=88.4 loss=0.2944 val_acc=86.6 val_loss=0.3752
Epoch 5: acc=89.4 loss=0.2643 val_acc=87.6 val_loss=0.3538
Epoch 6: acc=90.0 loss=0.2186 val_acc=87.6 val_loss=0.3524
Epoch 7: acc=90.5 loss=0.2137 val_acc=87.8 val_loss=0.3457
Epoch 8: acc=90.9 loss=0.2053 val_acc=87.9 val_loss=0.3427
Epoch 9: acc=91.3 loss=0.1631 val_acc=88.4 val_loss=0.3380
Epoch 10: acc=91.7 loss=0.1727 val_acc=88.3 val_loss=0.3444
Epoch 11: acc=92.1 loss=0.1566 val_acc=88.1 val_loss=0.3493
Epoch 12: acc=92.5 loss=0.1547 val_acc=88.4 val_loss=0.3470
Epoch 13: acc=92.9 loss=0.1138 val_acc=88.4 val_loss=0.3592
Epoch 14: acc=93.2 loss=0.1596 val_acc=88.6 val_loss=0.3732
Epoch 15: acc=93.5 loss=0.1401 val_acc=88.3 val_loss=0.3810
Epoch 16: acc=93.8 loss=0.1428 val_acc=88.0 val_loss=0.4006
Epoch 17: acc=94.0 loss=0.0788 val_acc=88.0 val_loss=0.4108
Epoch 18: acc=94.3 loss=0.1134 val_acc=88.2 val_loss=0.4374
Epoch 19: acc=94.5 loss=0.0725 val_acc=88.0 val_loss=0.4463
Epoch 20: acc=94.7 loss=0.2041 val_acc=88.1 val_loss=0.4503
FinishedF.3.5 Visualisierung
Wir sehen uns den Verlauf des Fehlers und der Accuracy über die Epochen an.
Vorab der Import und eine Hilfsfunktion.
import matplotlib.pyplot as pltdef set_subplot(ax, erange, y_label, traindata, testdata, ylim):
ax.plot(erange, traindata, 'b', label='Training')
ax.plot(erange, testdata, 'g', label='Validation')
ax.set_xlabel('Epochs')
ax.set_ylabel(y_label)
ax.legend()
ax.grid()
ax.set_ylim(ylim)
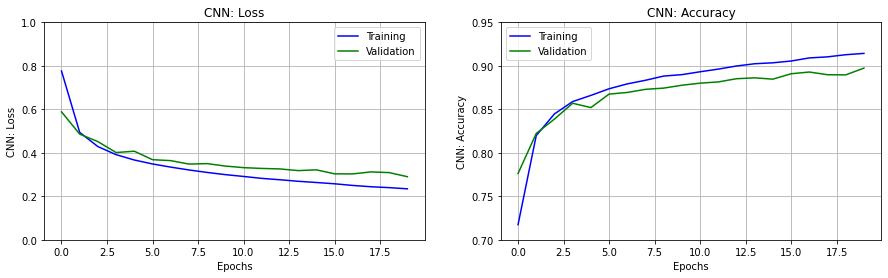
ax.set_title(y_label)Wir zeichnen Loss und Accuracy jeweils für Trainingsdaten (blaue) und Testdaten (grün).
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(15,4))
erange = range(epochs)
set_subplot(ax[0], erange, 'FNN: Loss', history1['loss'],
history1['val_loss'], [0,1])
set_subplot(ax[1], erange, 'FNN: Accuracy', history1['acc'],
history1['val_acc'], [70,95])
plt.show()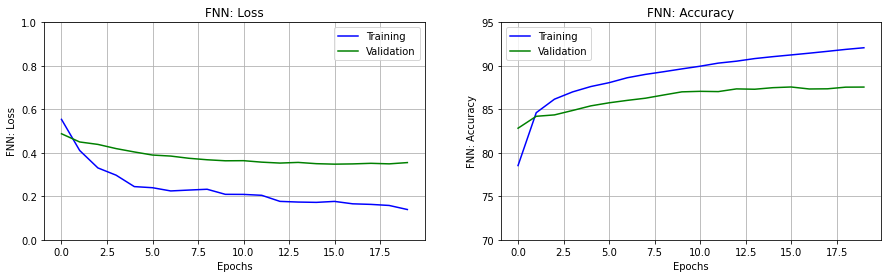
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(15,4))
erange = range(epochs)
set_subplot(ax[0], erange, 'CNN: Loss', history2['loss'],
history2['val_loss'], [0,1])
set_subplot(ax[1], erange, 'CNN: Accuracy', history2['acc'],
history2['val_acc'], [70,95])
plt.show()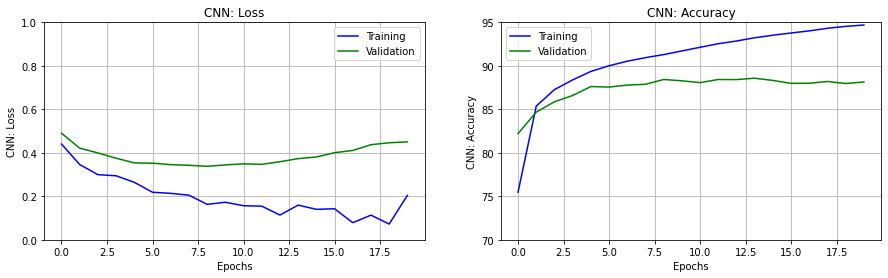
F.4 Vergleich mit Keras
Hier wollen wir uns das identische CNN in Keras ansehen.
from tensorflow import keras
keras.__version__'2.7.0'F.4.1 Netz
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten, Conv2D, MaxPool2D
k_cnn = Sequential()
k_cnn.add(Conv2D(filters=6,
kernel_size=5,
activation='relu',
input_shape=(28,28,1)))
k_cnn.add(MaxPool2D(pool_size=2, strides=2))
k_cnn.add(Conv2D(filters=16,
kernel_size=5,
activation='relu'))
k_cnn.add(Flatten())
k_cnn.add(Dense(80, activation='relu'))
k_cnn.add(Dense(10, activation='softmax')) # ohne Softmax funktioniert es nicht
k_cnn.summary()Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_2 (Conv2D) (None, 24, 24, 6) 156
max_pooling2d_1 (MaxPooling (None, 12, 12, 6) 0
2D)
conv2d_3 (Conv2D) (None, 8, 8, 16) 2416
flatten_1 (Flatten) (None, 1024) 0
dense_2 (Dense) (None, 80) 82000
dense_3 (Dense) (None, 10) 810
=================================================================
Total params: 85,382
Trainable params: 85,382
Non-trainable params: 0
_________________________________________________________________Hier zum Vergleich nochmal die PyTorch-Definition:
class ConvNet(nn.Module):
def __init__(self):
super().__init__()
self.layers = nn.Sequential(
nn.Conv2d(1, 6, kernel_size = 5),
nn.ReLU(),
nn.MaxPool2d(2, 2),
nn.Conv2d(6, 16, kernel_size = 5),
nn.ReLU(),
nn.Flatten(),
nn.Linear(16 * 8 * 8, 80),
nn.ReLU(),
nn.Linear(80, 10)
)
def forward(self, x):
return self.layers(x)
cnn = ConvNet()
print(cnn)ConvNet(
(layers): Sequential(
(0): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
(1): ReLU()
(2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(3): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
(4): ReLU()
(5): Flatten(start_dim=1, end_dim=-1)
(6): Linear(in_features=1024, out_features=80, bias=True)
(7): ReLU()
(8): Linear(in_features=80, out_features=10, bias=True)
)
)F.4.2 Daten
from tensorflow import keras
fashion_mnist = keras.datasets.fashion_mnist
(x_train, y_train), (x_test, y_test) = fashion_mnist.load_data()import numpy as np
# Normalisieren
x_train = x_train / 255.0
x_test = x_test / 255.0
# Um Kanal erweitern
x_train = np.expand_dims(x_train, -1)
x_test = np.expand_dims(x_test, -1)x_train.shape(60000, 28, 28, 1)from tensorflow.keras.utils import to_categorical
y_train = to_categorical(y_train, 10)
y_test = to_categorical(y_test, 10)y_train.shape(60000, 10)import matplotlib.pyplot as plt
plt.imshow(x_train[0])
plt.show()
y_train[0]array([0., 0., 0., 0., 0., 0., 0., 0., 0., 1.], dtype=float32)optimizer = keras.optimizers.SGD(learning_rate=learning_rate)
k_cnn.compile(loss='categorical_crossentropy',
optimizer=optimizer,
metrics=['acc'])k_history = k_cnn.fit(x_train, y_train,
epochs=epochs,
validation_data=(x_test, y_test))2022-04-16 02:27:13.127982: W tensorflow/core/platform/profile_utils/cpu_utils.cc:128] Failed to get CPU frequency: 0 Hz
2022-04-16 02:27:13.281279: I tensorflow/core/grappler/optimizers/custom_graph_optimizer_registry.cc:112] Plugin optimizer for device_type GPU is enabled.Epoch 1/20
1872/1875 [============================>.] - ETA: 0s - loss: 0.7766 - acc: 0.71732022-04-16 02:27:24.181843: I tensorflow/core/grappler/optimizers/custom_graph_optimizer_registry.cc:112] Plugin optimizer for device_type GPU is enabled.1875/1875 [==============================] - 13s 7ms/step - loss: 0.7764 - acc: 0.7174 - val_loss: 0.5885 - val_acc: 0.7762
Epoch 2/20
1875/1875 [==============================] - 12s 7ms/step - loss: 0.4939 - acc: 0.8198 - val_loss: 0.4860 - val_acc: 0.8223
Epoch 3/20
1875/1875 [==============================] - 12s 7ms/step - loss: 0.4287 - acc: 0.8447 - val_loss: 0.4515 - val_acc: 0.8388
Epoch 4/20
1875/1875 [==============================] - 12s 7ms/step - loss: 0.3915 - acc: 0.8589 - val_loss: 0.4013 - val_acc: 0.8570
Epoch 5/20
1875/1875 [==============================] - 12s 7ms/step - loss: 0.3670 - acc: 0.8660 - val_loss: 0.4075 - val_acc: 0.8520
Epoch 6/20
1875/1875 [==============================] - 12s 7ms/step - loss: 0.3488 - acc: 0.8736 - val_loss: 0.3685 - val_acc: 0.8675
Epoch 7/20
1875/1875 [==============================] - 12s 7ms/step - loss: 0.3343 - acc: 0.8792 - val_loss: 0.3641 - val_acc: 0.8694
Epoch 8/20
1875/1875 [==============================] - 13s 7ms/step - loss: 0.3212 - acc: 0.8834 - val_loss: 0.3482 - val_acc: 0.8730
Epoch 9/20
1875/1875 [==============================] - 12s 7ms/step - loss: 0.3098 - acc: 0.8882 - val_loss: 0.3504 - val_acc: 0.8744
Epoch 10/20
1875/1875 [==============================] - 12s 7ms/step - loss: 0.2997 - acc: 0.8899 - val_loss: 0.3391 - val_acc: 0.8777
Epoch 11/20
1875/1875 [==============================] - 12s 7ms/step - loss: 0.2913 - acc: 0.8932 - val_loss: 0.3319 - val_acc: 0.8801
Epoch 12/20
1875/1875 [==============================] - 12s 7ms/step - loss: 0.2825 - acc: 0.8963 - val_loss: 0.3282 - val_acc: 0.8815
Epoch 13/20
1875/1875 [==============================] - 12s 7ms/step - loss: 0.2762 - acc: 0.8998 - val_loss: 0.3259 - val_acc: 0.8852
Epoch 14/20
1875/1875 [==============================] - 12s 7ms/step - loss: 0.2691 - acc: 0.9024 - val_loss: 0.3182 - val_acc: 0.8862
Epoch 15/20
1875/1875 [==============================] - 13s 7ms/step - loss: 0.2635 - acc: 0.9035 - val_loss: 0.3217 - val_acc: 0.8847
Epoch 16/20
1875/1875 [==============================] - 12s 7ms/step - loss: 0.2576 - acc: 0.9056 - val_loss: 0.3035 - val_acc: 0.8909
Epoch 17/20
1875/1875 [==============================] - 13s 7ms/step - loss: 0.2500 - acc: 0.9091 - val_loss: 0.3030 - val_acc: 0.8929
Epoch 18/20
1875/1875 [==============================] - 12s 7ms/step - loss: 0.2440 - acc: 0.9103 - val_loss: 0.3122 - val_acc: 0.8898
Epoch 19/20
1875/1875 [==============================] - 13s 7ms/step - loss: 0.2399 - acc: 0.9128 - val_loss: 0.3090 - val_acc: 0.8896
Epoch 20/20
1875/1875 [==============================] - 13s 7ms/step - loss: 0.2344 - acc: 0.9143 - val_loss: 0.2903 - val_acc: 0.8974fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(15,4))
erange = range(epochs)
set_subplot(ax[0], erange, 'CNN: Loss', k_history.history['loss'],
k_history.history['val_loss'], [0,1])
set_subplot(ax[1], erange, 'CNN: Accuracy', k_history.history['acc'],
k_history.history['val_acc'], [0.70,0.95])
plt.show()