10 Transformationen

In diesem Kapitel beschäftigen wir uns mit Computergrafik im 2D-Raum. Bislang können wir einfache Formen zeichnen und mit Hilfe von Variablen animieren. Jetzt lernen wir drei mächtige Operationen kennen, um Formen zu verschieben, zu drehen und zu vergrößeren/verkleinern. Diese Operationen lassen sich auch in Animationen verwenden.

Hier zwei Beispiele von Programmen, die Sie zum Ende des Kapitels programmieren können:

10.1 Einführung am Beispiel der Translation

Eine Translation ist eine Verschiebung, zunächst mal im 2D-Raum. In Processing gibt es dafür den Befehl translate().

Falls Sie schon mit Translationen rumgespielt haben und denken, dass damit "Objekte" verschoben werden, dann folgen Sie bitte genau den Ausführungen, um etwaige Missverständnisse auszuräumen. Sie verschieben keine Objekte, sondern den ganzen Raum! Statt "Raum" sagen wir hier auch "Koordinatensystem" oder "Leinwand".

Nehmen wir ein Rechteck an einer bestimmten Position (10, 10).

// Unser Rechteck...
rect(10, 10, 30, 20);

Wenn wir das an Position (50, 50) zeichnen wollen, dann können wir (50, 50) als neue Koordinaten angeben.

// ...soll an Position (50, 50)
// Lösung 1:
rect(50, 50, 30, 20);

Alternative: Wir lassen das Rechteck bei (10, 10) und "verschieben die Leinwand" um 40 Pixel nach unten und um 40 Pixel nach rechts. Man kann auch sagen, wir verschieben die Leinwand um den Vektor (40, 40). Das können Sie mit dem Befehl translate() tun und geben dort entsprechend den Verschiebungsvektor (40, 40) an.

// Lösung 2: verschiebe erst Koordinatensystem um (40, 40)
// und zeichne dann
translate(40, 40);
rect(10, 10, 30, 20);

Stellen Sie sich das wie folgt vor: Erst wird die Leinwand um (40, 40) verschoben, dann wird das Rechteck an Position (10, 10) im verschobenen Koordinatensystem gezeichnet.

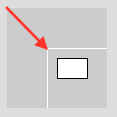
Ganze Bilder verschieben

Der Vorteil? Sie können ganze Bilder verschieben! Erinnern Sie sich an eine der ersten Übungen, wo man eine Figur an die Maus klebt? Man wählte einen Ankerpunkt (mouseX, mouseY) und definierte die anderen Koordinaten relativ dazu. Ziemlich umständlich:

// Zeichnung klebt an Maus 1
// Arbeit mit Offsets vom Ankerpunkt (mouseX, mouseY)

void draw() {
  background(100);


  // Haus:
  rect(mouseX,mouseY+20,30,20);
  triangle(mouseX,mouseY+20,mouseX+30,mouseY+20,
           mouseX+15,mouseY);
 
}

Mit dem Befehl translate() können das Bild auf das feste Koordinatensystem malen und später das gesamte Koordinatensystem bewegen, in diesem Fall mit translate(mouseX, mouseY):

// Zeichnung klebt an Maus 2
// Verschiebung des Koordinatensystems um (mouseX, mouseY)

void draw() {
  background(100);

  // Verschiebe Koordinatensystem zur Maus
  translate(mouseX, mouseY);

  // Haus:
  rect(0,20,30,20);
  triangle(0,20,30,20,15,0);
}

Auswirkung mehrerer Translates

Translationen können mehrfach durchgeführt werden. Dabei wird das Koordinatensystem (das "Bild") immer weitergeschoben. Nehmen wir wieder das Beispiel mit dem Rechteck:

translate(40, 40);
translate(10, 20);
rect(10, 10, 30, 20);

Wird "zwischendurch" etwas gezeichnet, wird immer die aktuelle Position des Koordinatensystems zugrunde gelegt.

translate(40, 40);
ellipse(0, 0, 20, 20);
translate(10, 20);
rect(10, 10, 30, 20);

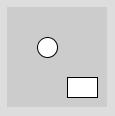
Das Koordinatensystem kann man sich auch als eine Art Schablone vorstellen, mit Hilfe derer ein Bild gezeichnet wird. Mit translate() wird die Schablone weitergeschoben.

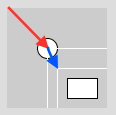
// Zeichnung klebt an Maus
// Lösung durch Verschiebung des Koordinatensystems

void draw() {
  background(100);
  fill(255,100);
  drawKoord(color(255, 0, 0));

  translate(mouseX, mouseY);
  drawKoord(color(0, 255, 0));

  // Haus:
  rect(0, 20, 30, 20);
  triangle(0, 20, 30, 20, 15, 0);

  // 50 Pixel nach rechts
  translate(50, 0);
  drawKoord(color(0, 0, 255));

  ellipse(0, 0, 20, 20);
}

void drawKoord(color col) {
  stroke(col);
  strokeWeight(4);
  line(0, 0, 10, 0); // x-Achse
  line(0, 0, 0, 10); // y-Achse
  strokeWeight(1);
  stroke(0);
}

Fingerübung

10.1 a) Translation

Nehmen Sie den folgenden Code:

rect(0, 0, 30, 30);
rect(0, 0, 30, 30);
rect(0, 0, 30, 30);

Fügen Sie zwei translate-Anweisungen ein, so dass Sie folgendes Resultat bekommen:

Lösung

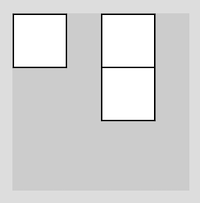
rect(0, 0, 30, 30);
translate(50, 0);
rect(0, 0, 30, 30);
translate(0, 30);
rect(0, 0, 30, 30);

10.2 Translation, Rotation, Skalierung

In Processing verwenden Sie hauptsächlich drei sogenannte affine Transformationen:

1. Translation (Verschiebung)
2. Rotation (Drehung)
3. Skalierung (Vergrößerung/Verkleinerung)

Diese Transformationen heißen affin (= verwandt, übereinstimmend), weil sie die prinzipielle Form eines Objekts nicht verändern.

Dank eines Tricks, den homogenen Koordinaten, lässt sich jede dieser Transformationen als eine Matrix ausdrücken. Und noch besser: Wenn man zwei Transformationen A und B hintereinander ausführen möchte, muss man lediglich die zugehörigen Matrizen MA und MB miteinander multiplizieren. Die resultierende Matrix repräsentiert dann die Kombination dieser zwei Transformationen. Das bedeutet, dass selbst tausende von Transformationen nach Multiplikation sich auf eine einzige Matrix verdichten.

Translation

Mit einer Translation verschiebt man das aktuelle Koordinatensystem um einen Vektor:

translate(x, y);

Das bedeutet, dass alle nachfolgenden Befehle sich auf dieses neue, verschobene Koordinatensystem beziehen, d.h. man kann komplexe Zeichnungen leicht verschieben, indem man die Befehle gemeinsam der Translation nachstellt.

void draw() {
  background(255);
  translate(mouseX, mouseY);

  // Gesicht
  ellipse(0,0,50,50);
  ellipse(-10,-10,8,8);
  ellipse(10,-10,8,8);
}

Wie hier das Gesicht, das der Maus folgt.

Animation mit Translate

Natürlich können Sie translate() auch zur Animation verwenden. Beachten Sie, dass Sie das Gesicht jetzt um den Nullpunkt herum zeichnen und anschließend das Koordinatensystem animieren.

int x = 0;

void draw() {
  background(255);
  translate(x, height/2);

  // Gesicht
  ellipse(0,0,50,50);
  ellipse(-10,-10,8,8);
  ellipse(10,-10,8,8);

  x++;
  if (x > width) {
    x = 0;
  }
}

Translation als Operation auf Vektoren

Wie macht Processing das eigentlich mit der Translation? Zunächst kann man sich vorstellen, dass jeder Punkt p im Grafikfenster als Vektor p = (px, py) verstanden wird. Eine Translation t kann man ebenfalls als Vektor t = (tx, ty) darstellen.

Mathematisch gesehen ist eine Verschiebung von Punkt p um den Vektor t eine Vektoraddition. Mann erhält den verschobenen Punkt p', indem man p und t addiert.

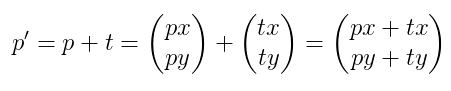
Eine Form wie eine Ellipse oder ein Rechteck besteht aus einer Reihe von Punkten p1, p2, ... pN. Wenn die gesamte Form um Vektor t verschoben werden soll, addiert man alle Punkte mit t und zeichnet die neuen Punkte p1', p2', ...

Rotation

Rotation bedeutet, dass das gesamte Koordinatensystem um den Ursprung gedreht wird. Der Winkel wird im Bogenmaß angegeben, d.h. der Wert sollte zwischen 0 und 2*PI liegen.

Wem das Bogenmaß nicht geheuer ist, der kann mit Grad rechnen (also 0° bis 360°) und die Funktion radians() benutzen, um von Grad zu Bogenmaß (engl. radian) umzurechnen.

rotate(angle);

// Rechteck ohne Rotation
rect(width/2, 0, 40, 20);

// Rotation um 45°
rotate(radians(45));

// Rechteck mit Rotation (schwarz)
fill(0);
rect(width/2, 0, 40, 20);

Hier sieht man deutlich, dass nicht etwa um eine Ecke des Objekts gedreht wird, sondern eben um den Ursprung (oben-links) des Koordinatensystems.

Wie dreht man dann z.B. um die linke obere Ecke des Rechtecks? Dazu verschiebt man das Koordinatensystem zunächst zum gewünschten Rotationspunkt und dreht erst dann:

// Rechteck ohne Rotation (weiß)
rect(width/2, 0, 40, 20);

// Translation zum linken, oberen Rechteckpunkt
translate(width/2, 0);

// Rotation um 45°
rotate(radians(45));

// Rechteck mit Rotation (schwarz)
// Jetzt bei (0, 0), da Koord.system verschoben
fill(0);
rect(0, 0, 40, 20);

Jetzt hat man die gewünschte Rotation:

Sie wollen um den Mittelpunkt rotieren? Dann bewegen Sie das Koordinatensystem in die Mitte des Rechtecks:

// Rechteck ohne Rotation (weiß)
rect(width/2, 0, 40, 20);

// Translation zur Mitte des Rechtecks
translate(width/2 + 20, 10);

// Rotation um 45°
rotate(radians(45));

// Rechteck mit Rotation (schwarz)
// Jetzt mit (0, 0) als Mitte
fill(0);
rect(-20, -10, 40, 20);

Animation mit Rotate

Auch Rotation kann man gut zur Animation verwenden:

float angle = 0;

void draw() {
  background(0);

  translate(50, 50); // geh zur Mitte
  rotate(angle); // drehe
  rect(0, -3, 50, 6); // zeichne Zeiger

  angle += radians(5); // in 5° Schritten
}

Hier der Zeiger in seiner Anfangsposition (angle = 0):

Hier mit Rotation:

Rotation als Operation auf Vektoren

Auch eine Rotation kann man als Operation auf einem Vektor p darstellen. Wir gehen aber erst im Abschnitt 14.4 darauf ein, weil dafür eine Matrix benötigt wird.

Skalierung

Skalierung wird auch vom Ursprung des Koordinatensystems aus gerechnet. Der Skalierungsfaktor liegt zwischen 0 und 1 (verkleinern) oder über 1 (vergrößern).

scale(factor);

Da die Skalierung vom Ursprung ausgeht, verschiebt sich das Objekt auch, wenn es nicht direkt auf dem Ursprung liegt:

rect(10, 10, 30, 20); // vorher

scale(2); // alles verdoppeln
fill(0); // schwarz

rect(10, 10, 30, 20); // nachher

Hier wird z.B. auch der Abstand der linken, oberen Ecke zum Ursprung verdoppelt:

Auch hier wieder der Trick mit dem vorherigen Verschieben. Die Endposition ist jetzt durch ein halbtransparentes Rechteck dargestellt.

rect(10, 10, 30, 20); // vorher

translate(10, 10);
scale(2); // alles verdoppeln
fill(0, 100); // schwarz, transparent
rect(0, 0, 30, 20); // nachher (jetzt auf 0, 0)

Jetzt wird das Rechteck vom linken, oberen Punkt aus skaliert, was intuitiver ist. Beachten Sie, dass auch der Rand (stroke) sich verdoppelt hat.

Animation mit Scale

Auch hier ein Beispiel für eine Animation:

float factor = 1;

void draw() {
  background(0);
  rectMode(CENTER);

  translate(50, 50); // geh zur Mitte
  scale(factor);
  rect(0, 0, 10, 10);

  factor += .1;
  if (factor > 12) {
    factor = 1;
  }
}

Skalierung in zwei Dimensionen

Sie können die Skalierung für die x- und y-Dimension getrennt angeben. Dann bekommt scale() zwei Parameter, jeweils für x- und y-Achse.

Hier wird nur in x-Richtung um Faktor 2 skaliert:

rect(10, 10, 30, 20);

scale(2, 1); // nur x verdoppeln
fill(0);

rect(10, 10, 30, 20);

Hier wird nur in y-Richtung um Faktor 2 skaliert:

rect(10, 10, 30, 20);

scale(1, 2); // nur y verdoppeln
fill(0);

rect(10, 10, 30, 20);

Skalierung als Operation auf Vektoren

Wenn wir wieder einen Punkt p als Vektor auffassen, muss Processing wieder den Punkt p' berechnen, der um einen Faktor s skaliert wurde. Mathematisch erreichen wir das durch die Multiplikaiton des Vektors p mit dem Skalar s (als "Skalar" bezeichnet man eine einfache Zahl, im Gegensatz zu einem Vektor):

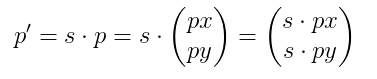
Beachten Sie, dass hier sowohl die x- als auch die y-Komponente um s skaliert werden.

Koordinatensystem sichtbar gemacht

Der Befehl translate() verschiebt das aktuelle Koordinatensystem, nicht die Objekte. Das ist etwas ungewohnt, da Sie eher gewohnt sind, Objekte zu verschieben. Es ist aber wichtig, dies so zu denken, damit die Reihenfolge Ihrer Operationen stimmt.

Folgendes Programm zeichnet das "aktuelle" Koordinatensystem aus Grid, um das Verständnis zu erleichtern:

void setup() {
}

void draw() {
  background(255);
  drawGrid(200); // normales Koord.sys.

  translate(50,50);
  drawGrid(150); // um (50,50) verschoben

  rotate(PI/8);
  drawGrid(0); // um 22,5° gedreht

  fill(255,0,0);
  rect(0,0,20,10); // Rechteck im Koord.sys
}

// Zeichnet das Koordinatensystem als Grid
void drawGrid(int greyscale) {
  stroke(greyscale);
  for (int x = 0; x < width; x += 10) {
    line(x, 0, x, height);
  }
    for (int y = 0; y < height; y += 10) {
    line(0, y, width, y);
  }
}

Man sieht, dass das rote Rechteck als Teil des verschobenen Koordinatensystems gezeichnet wird.

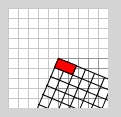
Verändert man die Reihenfolge der Operationen, ergibt sich ein gänzlich anderes Bild:

void draw() {
  background(255);
  drawGrid(200);

  rotate(PI/8);
  drawGrid(150); // um 22,5° gedreht

  translate(50, 50);
  drawGrid(0); // um (50,50) verschoben

  fill(255, 0, 0);
  rect(0, 0, 20, 10);
}

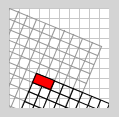
Verschachtelte Animation

Interessant wird es, wenn wir Animationen verschachteln, indem wir innerhalb eines bewegten lokalen Koordinatensystems eine weitere Animation erzeugen.

Wir betrachten zunächst einen einfachen "Rotor". Die Linie findet sich in einem Koordinatensystem, das durch eine Translation und eine Rotation entsteht. Durch Veränderung von a entsteht die Drehung.

float a = 0;

void setup() {
  size(300, 300);
  strokeWeight(3);
}

void draw() {
  background(0);

  translate(width/2, height/2);
  rotate(a);
  stroke(255);
  line(-100, 0, 100, 0);

  a += .03;
}

Jetzt fügen wir im Koordinatensystem des Rotors einen zweiten Rotor hinzu. Dazu benötigen wir eine zweite Variable a2, um den Winkel des zweiten Rotors zu steuern (man kann natürlich auch a verwenden, dann haben beide Rotoren die gleiche Geschwindigkeit).

Wir erinnern uns, dass am Ende von draw() alle Transformationen zurückgesetzt werden, sonst würde diese Animation so nicht funktionieren.

float a = 0;
float a2 = 0;

void setup() {
  size(300, 300);
  strokeWeight(3);
}

void draw() {
  background(0);

  translate(width/2, height/2);
  rotate(a);
  stroke(255);
  line(-100, 0, 100, 0);

  translate(100, 0);
  rotate(a2);
  line(-30, 0, 30, 0);

  a += .03;
  a2 += .02;
}

Schaffen Sie es, einen dritten Rotor hinzuzufügen?

Sie können Animation immer auch dazu verwenden, generativ Zeichnungen zu erzeugen:

Versuchen Sie, obige Animation zu erzeugen. Sie benutzen dazu die Rotoren von oben und ein bisschen Farbe.

Fingerübungen

10.2 a) Rotation 1

Nehmen Sie den folgendes Rechteck:

rect(50, 0, 40, 20);

Rotieren Sie es so, dass es wie folgt aussieht:

Verwenden Sie dabei das Bogenmaß, d.h. nutzen Sie PI.

Lösung

rotate(PI/4);
rect(50, 0, 40, 20);

10.2 b) Rotation 2

Versuchen Sie, folgende Rotation zu erreichen:

Verwenden Sie dabei eine Kombination aus translate und rotate.

Lösung

translate(50, 0);
rotate(PI/4);
rect(0, 0, 40, 20);

Übungsaufgaben

10.2 a) Transformationen kombinieren   Level 21 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Versuchen Sie, die folgenden Formen herzustellen, indem Sie die drei Transformationen translate, rotate und scale verwenden.

Zeichnen Sie die Formen am besten immer um den Nullpunkt herum und schalten Sie entsprechende Transformation davor. Denken Sie daran, dass Sie bei jeder Transformation das gesamte Koordinatensystem bewegen.

Versuchen Sie, jede Form zunächst "theoretisch" zu lösen (im Kopf oder auf Papier). Wenn Sie lediglich Code-Zeilen hin und herschieben, bauen Sie evtl. kein wirkliches Verständnis auf...

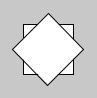
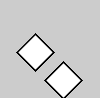
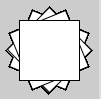
Bei einigen Figuren ist eine For-Schleife hilfreich. Denken Sie daran, dass bei jedem Schleifendurchlauf sämtliche Transformationen der vorherigen Durchläufe noch gültig sind!

10.2 b) Rotierendes Quadrat   Level 21 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Programmieren Sie ein Quadrat, das sie im Uhrzeigersinn um seine Mitte dreht. Verwenden Sie rotate und translate (in welcher Reihenfolge?).

10.2 c) Rotation mit zwei Formen   Level 21 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Lassen Sie einen Kreis um ein Rechteck rotieren. Programmieren Sie zwei Varianten. In der ersten bleibt das Rechteck statisch:

In der zweiten Variante dreht es sich mit:

10.2 d) Pulsierender Kreis   Level 21 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Programmieren Sie einen Kreis mit Durchmesser 50, der pulsiert. Er vergrößert sich auf das Doppelte und verkleinert sich dann auf die Hälfte usw. Verwenden Sie scale und translate (in welcher Reihenfolge?).

Lassen Sie den Skalierungsfaktor nie negativ werden.

Tipp

Gehen Sie ähnlich vor wie bei einem Ball, der von der Wand abprallt. Dort benötigen Sie eine Variable für x und eine für xspeed. Letztere "drehen sie um", wenn der Ball abprallt. Analog haben Sie beim Pulsieren eine Variable für die Skalierung - und eine weitere?

10.2 e) Schieben und Drehen   Level 31 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Lassen Sie ein Quadrat von links nach rechts fliegen, das sich um seinen Mittelpunkt dreht.

Tipp

Verwenden Sie translate und rotate. Das Rechteck zentrieren Sie am besten um den Ursprung (0,0).

10.2 f) Schieben und Drehen II   Level 41 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Fügen Sie ein zweites Quadrat hinzu und rotieren Sie es in die Gegenrichtung.

Solange Sie noch nicht pushMatrix kennen, ist das ein bisschen knifflig. Versuchen Sie im ersten Schritt nur das zweite Quadrat hinzuzufügen:

Anschließend kümmern Sie sich um die Rotation (siehe auch den Tipp).

Versuchen Sie mit möglichst wenig Variablen auszukommen (es reichen zwei!).

Tipp

Sie müssen nach der Rotation beim ersten Quadrat die Rotation wieder "rückgängig machen", indem Sie in die Gegenrichtung rotieren.

10.3 Objekt-Raum und Welt

Was genau ist eine Transformation? Wenn Sie ein Rechteck nehmen...

rect(0,0,50,30);

... dann können Sie es z.B. verschieben:

translate(20, 20);
rect(0,0,50,30);

Das bedeutet, dass z.B. der linke oberen Punkt jetzt nicht mehr bei (0, 0) liegt, sondern bei (20, 20). Eine Transformation ist also eine Abbildung (ein Mapping) von Punkten aus einem Ursprungsraum (wo das Rechteck ohne Transformation gezeichnet werden würde) in einen Zielraum. Wir nennen den Ursprungsraum auch Objektraum (object space) und den Zielraum einfach die Welt (world space).

In grafischen Anwendungen (2D und 3D) zeichnen Sie ein Objekt (z.B. Spielerfigur oder Küchenschrank) zunächst im Objektraum und wählen dort einen günstigen Ursprungspunkt (wichtig für Rotationen) und Maßstab (bei bestimmten Anwendungen z.B. Meter oder Millimeter). Erst in der Applikation (z.B. Computerspiel oder Küchenplanungs-Tool) wird das Objekt zunächst skaliert, falls in der Welt ein anderer Maßstab herrscht, und dann an die richtige Position geschoben (Translation) und rotiert.

Programmiertechnisch können Sie das deutlich machen, indem Sie den Zeichencode in eine Funktion auslagern. Innerhalb der Funktion zeichnen Sie im "Objekt-Raum". Processing sorgt aber dafür, dass alle zuvor angegebenen Transformationen das Objekt korrekt "in die Welt" zeichnet:

void draw() {
  background(100);
  translate(mouseX, mouseY);
  drawHaus();
}

// Haus im Objekt-Raum
void drawHaus() {
  rect(0,20,30,20);
  triangle(0,20,30,20,15,0);
}

Problem Kollisionsberechnung: Ein Problem, das sich daraus ergibt, ist, dass verschiedene Objekte in verschiedenen Koordinatensystemen leben. Bei der Kollisionsberechnung muss man dies berücksichtigen.

10.4 Transformationen als Matrizen

Mathematisch kann jede der drei Transformationen (Rotation, Translation, Skalierung) als Matrix M ausgedrückt werden. Um einen Punkt (x, y) aus dem Ursprungsraum zu dem entsprechenden Punkt (x', y') im Zielraum zu überführen, interpretiert man die Punkte als Vektoren (v bzw. v') und kann durch einfache Multiplikation den Zielpunkt v' herausbekommen:

v' = M v

Der sensationelle Effekt dieser Rechnung ist, dass Sie mehrere Transformationen, die hintereinander ausgeführt werden sollen, einfach dazumultiplizieren können. Wird z.B. nach Transformation M noch eine Transformation K durchgeführt, so rechnen Sie:

v' = M K v

Die Matrizenmultiplikation M K ergibt eine neue Matrix Q, so dass Sie ab sofort nur die ausmultiplizierte Matrix Q verwenden können.

v' = Q v

Das heißt: Die Matrixdarstellung erlaubt eine extrem kompakte Repräsentation aller Transformationen.

Transformations-Matrizen

Die Matrix für Skalierung ist ziemlich einfach:

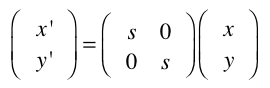
Man sieht direkt, dass man Ausmultiplikation, das jeweilige x bzw. y mit dem Skalierungsfaktor s multipliziert wird. In Processing wird also diese Matrix verwendet, wenn Sie folgendes schreiben (wobei s eine vorab definierte Variable sei):

scale(s);

Schauen Sie sich das gern mal an mit:

scale(2);
printMatrix();

Die Konsole zeigt:

2,0000  0,0000  0,0000
0,0000  2,0000  0,0000

(Was die rechte Spalte bedeutet, wird später klar.)

Die Matrix für Rotation können wir uns herleiten. Nehmen wir an, wir möchten Punkt (x, y) um Winkel alpha drehen. Nach der Drehung hat der Punkt die Position (x', y'):

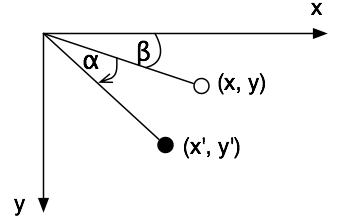
Wie berechnen wir (x', y')? Wie Sie oben sehen, nennen wir den Winkel der Linie zum ursprünglichen Punkt (x, y) beta. Wenn wir jetzt x' und y' berechnen wollen, können wir das folgende rechtwinklige Dreieck betrachten:

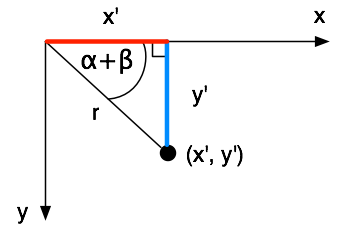
Die Strecke von Ursprung zu (x, y) haben wir r genannt. Jetzt können wir im rechtwinkligen Dreieck jeweils den Sinus- und Cosinussatz einsetzen:

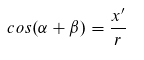
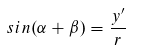
Wir lösen nach den gesuchten x' und y' auf:

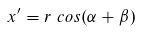
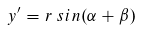
Jetzt wenden die Additionstheorme an:

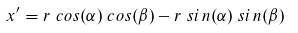
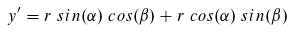
Jetzt haben wir Gleichungen für unsere gesuchten Variablen x' und y', aber wir kennen weder r noch beta. Um diese beiden Größen zu verarbeiten, betrachten wir ein anderes rechtwinkliges Dreieck - mit dem ursprünglichen Punkt (x, y):

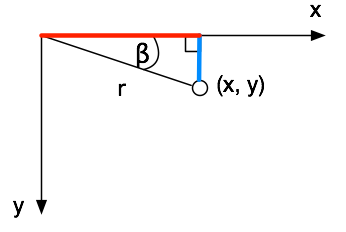
Auch hier können wir wieder Sinus- und Kosinussatz anwenden:

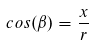
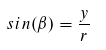
Diese zwei Gleichungen können wir oben einsetzen! Dadurch verschwindet sowohl beta als auch r. Wir erhalten:

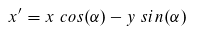
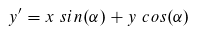
Diese Gleichungen können wir auch als Multiplikation mit einer Matrix formulieren. Die Rotation (im Uhrzeigersinn) wird also durch folgende Matrix erreicht:

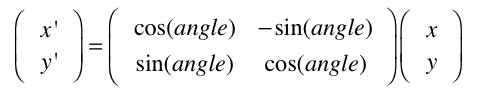
Dies entspricht dem Processing-Code (wobei angle eine vorab definierte Variable sei):

rotate(angle);

Wie funktioniert Translation? Das Problem ist, dass Sie dies nicht ohne weiteres durch Matrizenmultiplikation erreichen können. Das wiederum ist schade, weil dann das oben genannte Killer-Feature der Matrixmultiplikation nicht mehr gelten würde.

Homogene Koordinaten

Um dieses Problem zu lösen, bedient man sich homogener Koordinaten. Man fügt jedem Vektor (Punkt) eine weitere Koordinate hinzu, die immer 1 ist. Jede 2x2-Matrix wird zu einer 3x3-Matrix gemacht.

Die Skalierungsmatrix sieht jetzt so aus:

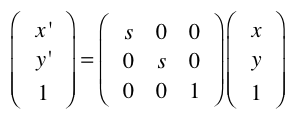
Die Rotationsmatrix so:

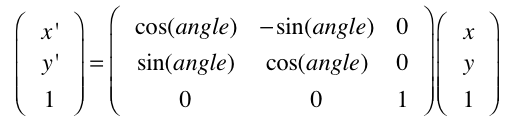
Wenn Sie nachrechnen, werden Sie merken, dass alles beim alten bleibt, nur dass immer die 1 mitgeschleppt wird. Dies zahlt sich bei der Translation aus, die wir jetzt wie folgt definieren können:

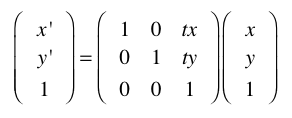
Wenn Sie nachrechnen, sehen Sie, dass wir für x' = x + tx und für y' = y + ty rausbekommen. Jetzt kann Processing in der gezeigten Weise Matrizen multiplizieren.

Probieren Sie es aus:

translate(30, 10);
printMatrix();

Auf der Konsole sehen Sie:

01,0000  00,0000  30,0000
00,0000  01,0000  10,0000

Jetzt ist auch klar, warum Sie, wenn Sie printMatrix() verwenden, drei Spalten sehen: es handelt sich um homogene Koordinaten. Die untere Zeile wird übrigens weggelassen, weil diese keine nennenswerte Information trägt (ist immer 0 0 1).

Aktuelle Transformationsmatrix

Wenn Sie mehrere Transformationen ausführen, multipliziert Processing dieses zusammen und speichert nur die aktuelle Matrix M. Diese Matrix können Sie sich jederzeit mit printMatrix() ausgeben lassen und mit getMatrix() bzw. pushMatrix()/popMatrix() zwischenspeichern, wie wir später sehen werden.

Zum Beispiel eine Translation um (10, 10), ausgedrückt durch Matrix K, und eine Skalierung um Faktor 2, ausgedrückt durch Matrix Q:

translate(10, 10); // Matrix K
printMatrix();
scale(2); // Matrix Q
printMatrix();

Intern wird gerechnet:

M = K Q

Zeigt auf der Konsole:

01,0000  00,0000  10,0000
00,0000  01,0000  10,0000

02,0000  00,0000  10,0000
00,0000  02,0000  10,0000

Die untere der beiden Matrizen ist die Matrix M.

10.5 Matrix speichern/wiederherstellen

Zur Einstimmung auf das Thema kann ich Ihnen den amüsanten Kurzfilm The Centrifuge Brain Project (2011) von Till Nowak ans Herz legen (insbes. auch den Abspann ab 6:08 beachten): Kurzfilm auf YouTube

Jetzt lernen wir, wie wir bei all den Transformationen einen "Zwischenzustand" speichern und später wiederherstellen können.

Wir wissen, dass jeder der Befehle transform, rotate, scale mit einer eigenen Matrix ausgedrückt wird. Noch wichtiger: Bei jedem Befehl wird die entsprechende Matrix auf die bestehende draufmultipliziert. Es gibt also zu jedem Zeitpunkt die Matrix, nennen wir Sie mal M.

Wenn Sie gar keine Transformationen ausführen, ist diese Matrix die Identität (Diagonalmatrix mit 1'sen). Wir nennen diese Matrix M0 und unser Ausgangs-Koordinatensystem nennen wir "System 0". M ist jetzt M0.

Wenn Sie z.B. eine Translation um (50, 0) durchführen, dann nennen wir die entsprechende Matrix M1. Jetzt wird M zu M0 * M1 (das ist wieder M1, da M0 die Identität ist).

Haben wir eine zweite Translation, z.B. um (0, 50), dann nennen wir diese Matrix M2 und M wird zu M0 * M1 * M2.

// Hier werden drei Koordinatensysteme gezeigt
// System 0: Ausgangssystem (rotes Rechteck)
// System 1: um 50px nach rechts verschoben (grünes Rechteck)
// System 2: um 50px nach rechts, 50px nach unten verschoben (blaues R.)

background(150);

printMatrix(); // Matrix M = M0 (Identität)

fill(255,0,0);
rect(0,0,30,20); // rotes Rechteck

translate(50,0); // Matrix M1

printMatrix();  // Matrix M = M0 * M1 (System 1)

fill(0,255,0);
rect(0,0,30,20); // grünes Rechteck

translate(0,50); // Matrix M2

printMatrix(); // Matrix M = M0 * M1 * M2 (System 2)

fill(0,0,255);
rect(0,0,30,20); // blaues Rechteck

Auf der Konsole sieht man die Matrix M zu den drei Zeitpunkten (Ausgangssystem, nach erster Translation, nach zweiter Translation):

1,0000  0,0000  0,0000
0,0000  1,0000  0,0000

01,0000  00,0000  50,0000
00,0000  01,0000  00,0000

01,0000  00,0000  50,0000
00,0000  01,0000  50,0000

Matrizendarstellung auf der Konsole: Processing zeigt uns die unterste Zeile der Matrix nicht an, da diese immer 0 0 1 ist (homogene Koordinaten).

Die Rechtecke sind jeweils am Ursprung von System 0 (rot), System 1 (grün) und System 2 (blau).

Jetzt wollen Sie am Ende des Codes wieder etwas in System 1 (grün) zeichnen, z.B. ein weißes Quadrat. Wie können Sie das tun, wenn es unbedingt am Ende des Codes sein muss? Ganz einfach: Sie speichern die Matrix M, nachdem Sie die erste Translation ausgeführt haben. Das geht mit pushMatrix() . Wenn Sie diese Matrix später wieder benötigen, rufen Sie popMatrix() auf und schon sind Sie in System 1.

background(150);

// Matrix M0 (Identität)

fill(255,0,0);
rect(0,0,30,20); // rotes Rechteck

translate(50,0); // Matrix M1 (System 1)
pushMatrix(); // System 1 speichern

fill(0,255,0);
rect(0,0,30,20); // grünes Rechteck

translate(0,50); // Matrix M2 (System 2)

fill(0,0,255);
rect(0,0,30,20); // blaues Rechteck

popMatrix(); // System 1 zurückholen
printMatrix();

fill(255);
rect(0,0,10,10); // NEU: weißes Quadrat

Das weiße Quadrat wird in System 1 (grün) gezeichnet:

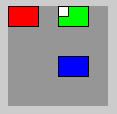
Auf der Konsole sehen Sie die Matrix nach dem popMatrix(): Es ist die Matrix von System 1 (vgl. mit Konsolenoutput oben).

01,0000  00,0000  50,0000
00,0000  01,0000  00,0000

Exkurs: Stack / Stapel

Die Befehle pushMatrix und popMatrix haben diese seltsamen Namen nicht ohne Grund. Dahinter verbirgt sich ein wichtiges Speichermodell der Informatik: der Stapel (engl. Stack).

Ein Stapel ist ein Speicher, der so funktioniert wie ein Stapel Bücher: Es kann immer nur etwas oben drauf gelegt werden und es kann immer nur von oben weggenommen werden.

Nehmen wir an, Sie kaufen Buch A. Dann legen Sie es auf einen leeren Stapel. Es liegt ganz "oben". Ihr Stapel sieht wie folgt aus:

A <-- oben

Man sagt auch, Sie pushen A auf Ihren Stapel. Sie kaufen jetzt Buch B und speichern es. Ihr Stapel ist gewachsen. Jetzt liegt B oben:

B <-- oben
A

Beachten Sie, dass Sie derzeit nicht an Buch A herankommen! Jetzt bekommen Sie ein drittes Buch C:

C <-- oben
B
A

Wenn Sie Buch C lesen wollen, dann holen Sie es vom Stapel. Man nennt diese Vorgang auch pop. Ihr neuer Stapel ist also:

B <-- oben
A

Sie möchten Buch A lesen? Dann müssen Sie erst Buch B holen:

A <-- oben

Erst jetzt dürfen Sie ein weiteres Mal pop ausführen und haben A. Ihr Stapel ist dann leer.

Wenn Sie mehr über Stapel erfahren möchten, schauen Sie sich den Wikipedia-Artikel Stapelspeicher an. Der Stapel ist insbesondere bei der Verarbeitung von Baumstrukturen (oder allgemeiner bei Graphen) eine wichtige Rolle, das können Sie z.B. in dem Artikel Depth First Traversal nachlesen.

Der Matrix-Stapel

Die Befehle pushMatrix und popMatrix machen nichts anderes, als die aktuelle Matrix M auf einen Stapel zu legen und wieder zu holen. Dadurch ist es möglich, mehrere Matrizen zu speichern.

Nehmen wir an, Sie wollen im obigen Beispiel auch ein weißes Quadrat in System 0 zeichnen, und zwar auch am Ende des Codes. Wie machen Sie das?

Antwort: Sie nutzen den Matrix-Stapel. Sie speichern die Matrix M ganz am Anfang auf dem Stapel (mit pushMatrix):

M (System 0) <-- oben

Dann speichern Sie die Matrix M nach der ersten Translation (wieder pushMatrix):

M (System 1) <-- oben
M (System 0)

Wenn Sie wie im alten Code popMatrix aufrufen, wird System 1 wiederhergestellt und der Stapel sieht so aus:

M (System 0) <-- oben

Das heißt, ganz zum Schluss machen Sie ein weiteres popMatrix(), um System 0 wiederherzustellen. Jetzt können Sie erneut ein weißes Quadrat zeichnen und der Matrix-Stapel ist leer.

background(150);

// Matrix M0 (Identität)
pushMatrix(); // System 0 speichern

fill(255,0,0);
rect(0,0,30,20); // rotes Rechteck

translate(50,0); // Matrix M1 (System 1)
pushMatrix(); // System 1 speichern

fill(0,255,0);
rect(0,0,30,20); // grünes Rechteck

translate(0,50); // Matrix M2 (System 2)

fill(0,0,255);
rect(0,0,30,20); // blaues Rechteck

popMatrix(); // System 1 zurückholen


fill(255);
rect(0,0,10,10); // weißes Quadrat

popMatrix(); // System 0 zurückholen (wieder Ausgangssystem)
printMatrix();

fill(255);
rect(0,0,10,10); // weißes Quadrat

Das weiße Quadrat wird jetzt auch in System 0 (rot) gezeichnet:

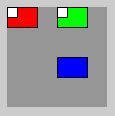
Auf der Konsole sehen Sie die Matrix von System 0, die Identität:

1,0000  0,0000  0,0000
0,0000  1,0000  0,0000

10.6 Artikulierte Strukturen

Artikulierte Strukturen gehören zu den fundamentalen Strukturen in der Computergrafik und Computeranimation. Insbesondere für die Animation von Körpern, egal ob Mensch oder Tier, sind diese Strukturen zentral. (Siehe z.B. den Artikel Animating Articulated Structures von Brian Lingard)

In diesem Abschnitt sehen wir, wie die Verwendung von Transformationen und von pushMatrix/popMatrix verwendet werden kann, um artikulierte Strukturen zu animieren.

Roboterarm

Ein Roboterarm, wie er z.B. in der Automobil-Fertigung eingesetzt wird, besteht aus festen Segmenten, die durch Gelenke (engl. joints) verbunden sind. Wenn wir uns das in 2D vorstellen, könnte das so aussehen:

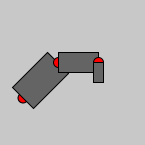
Die grauen Rechtecke sind die Segmente, die roten (Halb-)Kreise sind die Gelenke/Joints.

Wir nennen die Gelenke von links nach rechts: 1, 2 und 3. Wenn wir einen echten Roboterarm am Gelenk 1 bewegen würden, müssten sich alle drei Segmente bewegen, z.B. so:

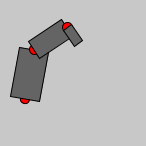
Wenn wir Gelenk 2 bewegen, werden nur die zwei kleineren Segmente bewegt:

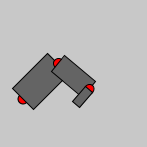
Das ist für uns selbstverständlich, weil wir es aus der Realität so kennen. Solche Systeme aus festen (rigiden) Segmenten, die über Gelenke verbunden sind, nennt man auch artikulierte Strukturen.

In der Grafikwelt müssen wir dieses Verhalten programmieren. Die Grundidee ist folgende: Jedes Gelenk ist der Ursprung eines neuen Koordinatensystems. Alle Strukturen, die an diesem Gelenk hängen, sind innerhalb dieses Koordinatensystems und werden also bei einer Rotation mitgedreht. In Processing können wir die normale Rotation verwenden, da diese immer um den Ursprung dreht.

Wenn jedes Gelenk ein eigenes Koordinatensystem „aufmacht“, wo wird dann das Segment gezeichnet? In unserem Fall bietet es sich an, das Segment am Ursprung beginnen zu lassen und dann nach rechts zu zeichnen.

Wir beginnen im statischen Modus in einem 150x150-Fenster und zeichnen das erste Segment als Rechteck der Größe 50x30. Der Ursprung soll genau dort sein, wo später das Segment rotiert wird, also auf der Mitte der linken Seite - deshalb sehen wir nur die untere Hälfe des Rechtecks:

size(150, 150);

// Armsegment 1
fill(100);
rect(0, -15, 50, 30);

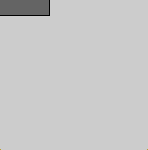
Wir schieben unseren "Arm" jetzt auf die Position (25, 100). Außerdem zeichnen wir das Gelenk als roten Punkt.

size(150, 150);

translate(25, 100);

// Gelenk1
fill(255,0,0);
ellipse(0, 0, 10, 10);

// Armsegment 1
fill(100);
rect(0, -15, 50, 30);

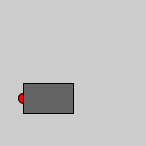
Dann fügen wir die zwei nächsten Segmente hinzu. Für jedes Segment verwenden wir ein translate(), um das Koordinatensystem zu verschieben. Denken Sie daran: Wir benötigen an jedem Gelenk eines Segments den Ursprung eines Koordinatensystems.

size(150, 150);

// Gelenk1
translate(25, 100);
fill(255,0,0);
ellipse(0, 0, 10, 10);

// Armsegment 1
fill(100);
rect(0, -15, 50, 30);

// Gelenk 2
translate(50, 0);
fill(255,0,0);
ellipse(0, 0, 10, 10);

// Armsegment 2
fill(100);
rect(0, -10, 40, 20);

// Gelenk 3
translate(40, 0);
fill(255,0,0);
ellipse(0, 0, 10, 10);

// Armsegment 3
fill(100);
rect(0, -5, 20, 10);

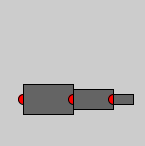
Um den Arm bewegen zu können, fügen wir jetzt Rotationen hinzu (und zuvor in den aktiven Modus wechseln). Die Rotationen werden vor dem Zeichnen der Gelenke eingefügt. Die Winkel sind globale Variablen, die sich später per Tastendruck ändern lassen.

float angle1 = -PI/4;
float angle2 = PI/4;
float angle3 = PI/2;

void setup() {
  size(150, 150);
}

void draw() {
  background(200);

  // Gelenk1
  translate(25, 100);
  rotate(angle1);
  fill(255, 0, 0);
  ellipse(0, 0, 10, 10);

  // Armsegment 1
  fill(100);
  rect(0, -15, 50, 30);

  // Gelenk 2
  translate(50, 0);
  rotate(angle2);
  fill(255, 0, 0);
  ellipse(0, 0, 10, 10);

  // Armsegment 2
  fill(100);
  rect(0, -10, 40, 20);

  // Gelenk 3
  translate(40, 0);
  rotate(angle3);
  fill(255, 0, 0);
  ellipse(0, 0, 10, 10);

  // Armsegment 3
  fill(100);
  rect(0, -5, 20, 10);
}

Jetzt möchten wir die Winkel interaktiv ändern. Die Tasten 1, 2 und 3 sollen den Winkel vergrößern. Mit SHIFT-Taste soll der Winkel verkleinert werden:

void keyPressed() {
  if (key == '1') {
    angle1 += 0.1;
  }
  if (key == '!') {
    angle1 -= 0.1;
  }
  if (key == '2') {
    angle2 += 0.1;
  }
  if (key == '\"') {
    angle2 -= 0.1;
  }
  if (key == '3') {
    angle3 += 0.1;
  }
  if (key == '§') {
    angle3 -= 0.1;
  }
}

(Interaktives Feld, verwenden Sie die Tasten 1, 2, 3 mit und ohne SHIFT/UMSCHALT)

Virtuelle Menschen

Virtuelle Menschen werden mit Hilfe eines Skeletts animiert. Ein Skelett besteht aus Gelenken und Segmenten (Knochen), genauso wie unser Roboterarm.

Die virtuellen Figuren, die Sie aus Filmen wie Toy Story oder Avatar kennen, bestehen aus dem Skelett und einem darübergelegtem Drahtgittermodell (engl. mesh). Animiert wird das Skelett und das Skelett wiederum bewegt das Drahtgitter. Nur das Gesicht wird häufig mit einer gesonderten Technik (z.B. Morph Targets) animiert.

Wir schauen uns den oberen Teil eines menschlichen Skeletts an, von der Hüfte (hip) über die Schultern (rshoulder = right shoulder, cshoulder = center between shoulders) bis zu Ellbogen (relbow/lelbow) und Hand (rhand/lhand). Links und rechts wird hier aus Sicht der Figur benannt.

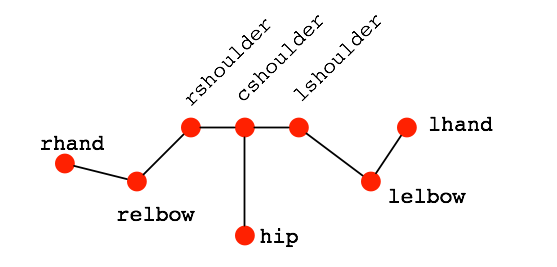
Der entscheidende Unterschied zum Roboterarm ist das Gelenk cshoulder, wo zwei Verbindungen abgehen.

Wir bauen zunächst unseren Torso von der Hüfte bis zur linken Schulter:

float aHip = -PI/2;

void setup() {
  size(300, 200);
}

void draw() {
  background(200);

  translate(width/2, 150);

  // Hüfte, Gelenk
  rotate(aHip);
  fill(255, 0, 0);
  ellipse(0, 0, 10, 10);

  // Hüfte, Segment
  fill(100);
  rect(0, -20, 80, 40);

  // Schulterzentrum, Gelenk
  translate(80,0);
  fill(255, 0, 0);
  ellipse(0, 0, 10, 10);

  // Linke Schulter, Gelenk
  translate(0,30);
  fill(255, 0, 0);
  ellipse(0, 0, 10, 10);
}

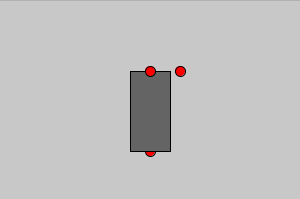
Wir steuern die Drehung an der Hüfte mit der Taste 0 mit und ohne UMSCHALT:

void keyPressed() {

  // Hüfte

  if (key == '0') {
    aHip += 0.1;
  }
  if (key == '=') {
    aHip -= 0.1;
  }
}

Jetzt fügen wir den linken Arm hinzu und definieren entsprechend drei Winkel. Der Arm ist fast identisch mit dem Roboterarm von oben:

float aLShoulder = PI/2;
float aLElbow = 0;
float aLHand = 0;

float aHip = -PI/2;

void setup() {
  size(300, 200);
}

void draw() {
  background(200);

  translate(width/2, 150);

  // Hüfte, Gelenk
  rotate(aHip);
  fill(255, 0, 0);
  ellipse(0, 0, 10, 10);

  // Hüfte, Segment
  fill(100);
  rect(0, -20, 80, 40);

  // Schulterzentrum, Gelenk
  translate(80,0);
  fill(255, 0, 0);
  ellipse(0, 0, 10, 10);

  // Linke Schulter, Gelenk
  translate(0,30);
  rotate(aLShoulder);
  fill(255, 0, 0);
  ellipse(0, 0, 10, 10);

  // Linke Schulter, Segment (Oberarm)
  fill(100);
  rect(0, -10, 50, 20);

  // Linker Elbogen, Gelenk
  translate(50, 0);
  rotate(aLElbow);
  fill(255, 0, 0);
  ellipse(0, 0, 10, 10);

  // Linker Elbogen, Segment
  fill(100);
  rect(0, -6, 40, 12);

  // Linke Hand, Gelenk
  translate(40, 0);
  rotate(aLHand);
  fill(255, 0, 0);
  ellipse(0, 0, 10, 10);

  // Linke Hand, Segment
  fill(100);
  rect(0, -3, 20, 6);
}

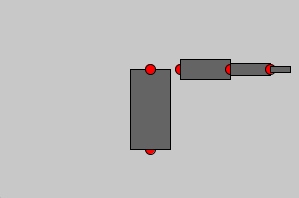
Und die entsprechende Tastensteuerung mit 1, 2, 3:

void keyPressed() {

  // Hüfte

  if (key == '0') {
    aHip += 0.1;
  }
  if (key == '=') {
    aHip -= 0.1;
  }

  // Linker Arm

  if (key == '1') {
    aLShoulder += 0.1;
  }
  if (key == '!') {
    aLShoulder -= 0.1;
  }
  if (key == '2') {
    aLElbow += 0.1;
  }
  if (key == '\"') {
    aLElbow -= 0.1;
  }
  if (key == '3') {
    aLHand += 0.1;
  }
  if (key == '§') {
    aLHand -= 0.1;
  }
}

Jetzt wollen wir den rechten Arm anfügen, aber wir haben ein Problem: Die rechte Schulter soll an das Schulterzentrum angefügt werden, am Ende des Codes befinden wir uns aber im Koordinatensystem der linken Hand. Dies ist genau die Stelle in der Abbildung oben, wo zwei Verbindungen vom Schulterzentrum ausgehen.

Hier hilft uns pushMatrix/popMatrix. Wir speichern das Koordinatensystem des Schulterzentrums zwischen (pushMatrix) und reaktivieren es (popMatrix) nach dem Zeichnen des linken Arms.

float aLShoulder = PI/2;
float aLElbow = 0;
float aLHand = 0;

float aRShoulder = -PI/2;
float aRElbow = 0;
float aRHand = 0;

float aHip = -PI/2;

void setup() {
  size(300, 200);
}

void draw() {
  background(200);

  translate(width/2, 150);

  // Hüfte, Gelenk
  rotate(aHip);
  fill(255, 0, 0);
  ellipse(0, 0, 10, 10);

  // Hüfte, Segment
  fill(100);
  rect(0, -20, 80, 40);

  // Schulterzentrum, Gelenk
  translate(80,0);
  fill(255, 0, 0);
  ellipse(0, 0, 10, 10);

  pushMatrix();

  // Linke Schulter, Gelenk
  translate(0,30);
  rotate(aLShoulder);
  fill(255, 0, 0);
  ellipse(0, 0, 10, 10);

  // Linke Schulter, Segment (Oberarm)
  fill(100);
  rect(0, -10, 50, 20);

  // Linker Elbogen, Gelenk
  translate(50, 0);
  rotate(aLElbow);
  fill(255, 0, 0);
  ellipse(0, 0, 10, 10);

  // Linker Elbogen, Segment
  fill(100);
  rect(0, -6, 40, 12);

  // Linke Hand, Gelenk
  translate(40, 0);
  rotate(aLHand);
  fill(255, 0, 0);
  ellipse(0, 0, 10, 10);

  // Linke Hand, Segment
  fill(100);
  rect(0, -3, 20, 6);

  popMatrix();

  // Rechte Schulter, Gelenk
  translate(0,-30);
  rotate(aRShoulder);
  fill(255, 0, 0);
  ellipse(0, 0, 10, 10);

  // Rechte Schulter, Segment (Oberarm)
  fill(100);
  rect(0, -10, 50, 20);

  // Rechter Elbogen, Gelenk
  translate(50, 0);
  rotate(aRElbow);
  fill(255, 0, 0);
  ellipse(0, 0, 10, 10);

  // Rechter Elbogen, Segment
  fill(100);
  rect(0, -6, 40, 12);

  // Rechte Hand, Gelenk
  translate(40, 0);
  rotate(aRHand);
  fill(255, 0, 0);
  ellipse(0, 0, 10, 10);

  // Rechte Hand, Segment
  fill(100);
  rect(0, -3, 20, 6);
}

Jetzt noch die Tastensteuerung mit 4, 5, 6 für den rechten Arm. Zu beachten ist hier, dass die Drehrichtung umgekehrt ist wie beim anderen Arm, denn: die Taste 1 dreht den linken Arm nach unten - wenn wir die Drehrichtung nicht ändern, würde Taste 4 den rechten Arm nach oben drehen. Jetzt drehen 1 und 4 jeweils den linken/rechten Oberarm nach unten.

void keyPressed() {

  // Hüfte

  if (key == '0') {
    aHip += 0.1;
  }
  if (key == '=') {
    aHip -= 0.1;
  }

  // Linker Arm

  if (key == '1') {
    aLShoulder += 0.1;
  }
  if (key == '!') {
    aLShoulder -= 0.1;
  }
  if (key == '2') {
    aLElbow += 0.1;
  }
  if (key == '\"') {
    aLElbow -= 0.1;
  }
  if (key == '3') {
    aLHand += 0.1;
  }
  if (key == '§') {
    aLHand -= 0.1;
  }

  // Rechter Arm (umgekehrte Drehrichtung)

  if (key == '4') {
    aRShoulder -= 0.1;
  }
  if (key == '$') {
    aRShoulder += 0.1;
  }
  if (key == '5') {
    aRElbow -= 0.1;
  }
  if (key == '%') {
    aRElbow += 0.1;
  }
  if (key == '6') {
    aRHand -= 0.1;
  }
  if (key == '&') {
    aRHand += 0.1;
  }
}

Das Resultat können Sie unten ausprobieren.

(Interaktives Feld, verwenden Sie die folgenden Tasten mit und ohne SHIFT/UMSCHALT: 0 für die Hüfte; 1, 2, 3 für den linken Arm; 4, 5, 6 für den rechten Arm)