5 Schleifen

Challenge

Was wollen Sie nach dem Durcharbeiten des Kapitels programmieren können?

Diesmal haben wir drei Vorschläge. Nehmen Sie sich vor, eine Funktion wie die Parabel zu visualisieren:

Dann animieren Sie im aktiven Modus eine ganze Reihe von Linien:

Schließlich probieren Sie, ein Schachbrett mit verschachtelten Schleifen zu programmieren. Dieses Schachbrett können Sie dank Schleifen beliebig groß machen.

Schaffen Sie das? Vielleicht picken Sie sich zwei von den drei Challenges heraus.

Sie finden die Aufgaben auch unter 5.2 (j), 5.3 (d) und 5.4 (g).

Mit Schleifen können Sie einen Code-Block wiederholt ausführen lassen. Das ist zum Beispiel dann nützlich, wenn Sie viele Objekte zeichnen wollen, Listen von Personen durchlaufen möchten und für vieles mehr.

Schleifen sind nach der If-Anweisung das zweite Konstrukt, um den Kontrollfluss Ihres Programms zu steuern. Diese beiden Konstrukte bilden die Grundpfeiler jeder Programmierung.

5.1 While-Schleife

Wir wissen bereits, dass eine If-Anweisung den Kontrollfluss eines Programms ändert. Statt Zeile für Zeile abzuarbeiten, kann Ihr Programm Zeile überspringen oder auch nicht, je nachdem ob eine bestimmt Bedingung erfüllt ist oder nicht.

Eine While-Schleife hat große Ähnlichkeit mit einer If-Anweisung. Auch hier wird der Kontrollfluss verändert, aber anstatt Zeilen zu überspringen, können Sie die Ausführung von Zeilen mehrfach wiederholen.

Nehmen wir an, Sie wollen etwas ausdrucken unter der Bedingung, dass die Variable foo kleiner als 3 ist:

int foo = 0;

if (foo < 3) {
   println("wow");
}

Hier wird ein Mal "wow" ausgedruckt. Wenn Sie statt "if" "while" schreiben, wiederholt Processing den Code so lange, wie die Variable foo kleiner als 3 ist.

int foo = 0;

// das kann dauern...
while (foo < 3) {
   println("wow");
}

Da sich foo nicht ändert, läuft die Schleife unendlich lang. Nicht gut. Man nennt das eine Endlosschleife. Auch ein beliebter Anfängerfehler. Die Lösung ist, foo bei jedem Durchlauf des Code-Blocks zu ändern.

int foo = 0;

// ein Ende ist in Sicht :)
while (foo < 3) {
   println("wow");
   foo = foo + 1;
}

Jetzt wird der Code-Block drei Mal durchlaufen. Beim ersten Mal ist foo gleich 0, also wird der Block durchlaufen. Beim zweiten Mal ist foo gleich 1, also wieder durch den Block. Beim dritten Mal ist foo gleich 2, also nochmal. Erst beim vierten Mal ist die Bedingung hinter while nicht mehr erfüllt und der Code-Block wird nicht mehr ausgeführt. Es geht weiter hinter der schließenden geschweiften Klammer.

Nach der While-Schleife geht es wieder regulär weiter im Code. Wir zeigen das, indem wir eine Anweisung anhängen. Diese wird immer ausgeführt:

int foo = 0;

while (foo < 3) {
  println("wow");
  foo = foo + 1;
}
println("fertig");

Tabelle

Man kann sich die Verarbeitung einer Schleife gut mit Hilfe einer Tabelle verdeutlichen.

In der Tabelle trägt man die Entwicklung des Werts der Laufvariablen ein (hier: foo). In einer weiteren Spalte sieht man, ob die Bedingung (foo < 3) für den jeweiligen Wert erfüllt ist oder nicht. In der letzten Spalte sehen wir die Schleifenaktion, die den Wert von foo erhöht.

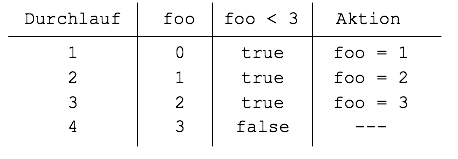
Tabellen sind immer dann hilfreich, wenn die Entwicklung der Laufvariablen komplizierter wird (rückwärts, andere Schrittweite) oder wenn weitere Variablen in Abhängigkeit von der Laufvariablen gesetzt werden sollen.

Flussdiagramm

Ähnlich wie bei der If-Anweisung, können wir den Kontrollfluss mit Hilfe eines Flussdiagramms visualisieren:

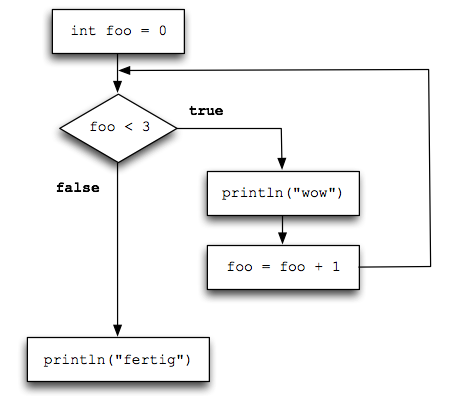
Das Diagramm ist fast identisch mit dem der If-Anweisung. Der einzige Unterschied ist, dass hier im true-Zweig ein Pfeil zurück zur Bedingung weist und damit Wiederholungen ermöglicht.

Begriffe

Die allgemeine Form der While-Schleife kann man so formulieren:

while (BEDINGUNG)
   ANWEISUNG

Die BEDINGUNG nennt man auch die Schleifenbedingung. Nur wenn diese Bedingung erfüllt ist, wird der Code in der Schleife ausgeführt (ähnlich wie beim If).

Das Gegenteil der Schleifenbedingung (die logische Negation) nennt man übrigens die Abbruchbedingung. In unserem Beispiel ist die Abbruchbedingung, dass foo größer-gleich 3 ist. Ein häufiger Fehler ist, dass statt der Schleifenbedingung die Abbruchbedingung eingesetzt wird.

Eine Variable, die hochgezählt (oder runtergezählt) wird und Teil der Schleifenbedingung ist, nennt man Laufvariable. Die Tatsache, dass die Laufvariable hochgezählt wird, nennt man auch die Schleifenaktion. Diese ist besonders wichtig, weil man sie leicht vergisst, was wiederum zur Folge hat, dass die Schleife nie abbricht (Endlosschleife) und Ihr Programm evtl. abstürzt.

Die ANWEISUNG in der allgemeinen Form der While-Schleife ist in der Regel ein Code-Block, d.h. eine oder mehr Zeilen Code, die von geschweiften Klammern umgeben sind.

Hier nochmal die Begriffe im Code:

int foo = 0; // Initialisierung der Laufvariable

while (foo < 3) { // Schleifenbedingung
  println("wow");
  foo = foo + 1; // Schleifenaktion
}
println("fertig");

Diese Begriffe sind insbesondere für die For-Schleife im nächsten Abschnitt wichtig.

Coding Style

Bitte achten Sie darauf, wo Leerzeichen und Zeilenumbrüche gemacht werden, und wo nicht.

while (i < 3) {
  println(i);
  i++;
}

Alternativ:

while (i < 3)
{
  println(i);
  i++;
}

Denken Sie auch daran, Ihre Code mit Bearbeiten > Autoformatierung von Processing korrekt einrücken zu lassen (Tastenkürzel STRG+T bzw. CMD+T).

int i = 1;

while (i <= 5) {
  println(i);
  i++;
}

int i = 0;

while (i < 5) {
  println(i+1);
  i++;
}

int anzahl = 3;

// jetzt Ihr Code...

###

while (BEDINGUNG)
   ANWEISUNG

int i = 0;

while (i < 3) {
   println("Runde " + i);
   i = i + 1;
}

5.2 For-Schleife

Die While-Schleife ist schlicht und elegant, kann aber zu Endlosschleifen führen, wenn man z.B. die Schleifenaktion vergisst. Eine weitere Beobachtung ist, dass fast immer eine Laufvariable eingeführt wird, die in der Schleifenbedingung genutzt und im Schleifenkörper verändert wird.

Da Informatiker von Natur aus faul sind, haben sie aus dieser Beobachtung heraus die For-Schleife erfunden. Die For-Schleife bietet ein kompaktes Wohlfühl-Paket für Schleifen mit Laufvariable mit relativ geringem Endlos-Risiko.

Nehmen wir an, Sie wollen wie im obigen Beispiel drei Mal "wow" drucken. Dann machen Sie das mit einer For-Schleife wie folgt:

for (int foo = 0; foo < 3; foo = foo + 1) {
   println("wow");
}

Ganz schön kurz, oder? Eine For-Schleife ist im Grunde eine Kurzschreibweise für die entsprechende While-Schleife:

int foo = 0; // 1. Initialisierung Laufvariable

while (foo < 3) // 2. Schleifenbedingung
{
   println("wow");
   foo = foo + 1; // 3. Schleifenaktion
}

Sie sehen oben die drei Komponenten einer While-Schleife mit Laufvariable: Initialisierung (eine Laufvariable wird erzeugt und initialisiert), Schleifenbedingung (nur unter dieser wird der Code-Block durchlaufen) und Schleifenaktion (wird nach Ausführung des Code-Blocks durchgeführt).

Die For-Schleife sieht allgemein so aus:

for (INTIALISIERUNG; BEDINGUNG; AKTION)
   ANWEISUNG

Sie können im Code-Block auf die Laufvariable zugreifen (z.B. um Sie auszugeben). Häufig wird die Laufvariable i genannt (wahrscheinlich für engl. increment), aber man kann natürlich beliebige Namen verwenden.

In der Schleifenaktion wird meist der Inkrementoperator ++ verwendet. Dieser erhöht die Variable um 1. Beispiel:

int x = 0;
println(x);
x++; // macht das gleiche wie x = x + 1;
println(x);

Analog gibt es den Dekrementoperator -- :

int x = 0;
println(x);
x--; // macht das gleiche wie x = x - 1;
println(x);

Die For-Schleife, die Sie also am häufigsten in irgendwelchem Code sehen werden, ist folgende:

for (int i = 0; i < 3; i++) {
   println(i);
}

Flussdiagramm

Falls Sie sich fragen, wie das Flussdiagramm einer For-Schleife aussieht:

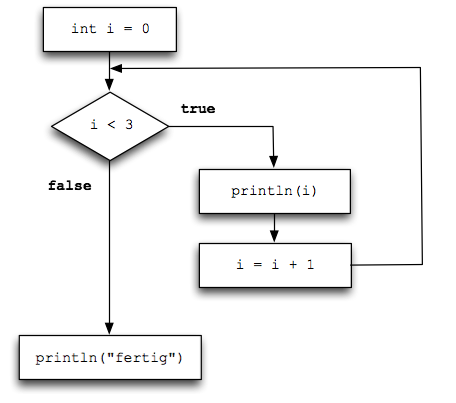
Sie sehen, dass es identisch mit dem der While-Schleife ist. Deshalb ist es auch so wichtig, dass man versteht, wie eine While-Schleife funktioniert, bevor man For-Schleifen verwendet. Eine For-Schleife ist nichts weiter als ein Spezialfall einer While-Schleife.

Die Syntax einer For-Schleife wirkt am Anfang etwas sperrig. Schreiben Sie viele davon und lassen Sie sich wie oben immmer die Laufvariable ausgeben, dann bekommen Sie schnell ein Gespür dafür. Beim Programmieren verwenden Sie für Wiederholungen fast immer die For-Schleife, es lohnt sich also...

Laufvariable ist lokal

Die Laufvariable Ihrer For-Schleife ist eine lokale Variable:

for (int i = 0; i < 5; i++) {
   // Laufvariable i ist lokal innerhalb der Schleife
   println(i);
}

Die Variable i wird im Kopf der Schleife (erste Zeile) deklariert und existiert für die Dauer der Schleife, also bis zur schließenden geschweiften Klammer. Das heißt, dass man nach der Schleife nicht mehr auf i zugreifen kann:

for (int i = 0; i < 5; i++) {
   println(i);
}
println(i); // FEHLER!

Sie können natürlich mehrere Schleifen hintereinander definieren, die alle eine Variable namens i verwenden. Es wird jedesmal eine neue Variable erzeugt.

// Variable i ist lokal
for (int i = 0; i < 5; i++) {
   println(i);
}

// Hier wird ein neue Variable i eingeführt
for (int i = 10; i > 0; i--) {
   println(i);
}

Beispiele für For-Schleifen

Rückwärts zählen

Sie können natürlich auch rückwärts durch die Zahlen gehen, wenn Sie die Initialisierung, Bedingung und Aktion entsprechend anpassen.

for (int i = 10; i > 0; i--) {
  println(i);
}

Ein häufiger Anfängerfehler ist hier, dass die Bedinung "falsch herum" gedacht wird, also i < 0. In diesem Fall wird die Schleife gar nicht ausgeführt, da i zu Beginn 10 ist, also nicht kleiner 0.

Jede zweite Zahl

Sie können auch in 2er-Schritten durch die Zahlen schreiten. Beachten Sie die Aktion.

for (int i = 0; i <= 10; i = i + 2) {
  println(i);
}

Summe

Eine typische Anwendung der For-Schleife ist die Berechnung der Summe 1 + 2 + 3 + ... + N, wobei N eine beliebige Zahl ist.

Eine wichtige Erkenntnis ist, dass dazu eine zusätzliche Variable zum Speichern der Zwischenergebnisse nötig ist.

int n = 5; // bis wohin gehen?

int summe = 0; // zum Aufsammeln

for (int i = 1; i <= n; i++) {
  summe = summe + i;
}

println(summe); // Ausgeben

Hier lohnt sich vielleicht der Blick auf eine Tabelle:

Historische Randnotiz: Der Mathematiker Carl Friedrich Gauß entdeckte im zarten Alter von neun eine Formel, mit der sich diese Summe in einem Schritt berechnen lässt. Die Formel nennt man auch den Kleinen Gauss. Alle, die mit neun noch kein Mathe-Genie waren, müssen sich wohl mit der For-Schleife begnügen...

Funktionsgraphen zeichnen

Lineare Funktionen

Mit einer Schleife kann man natürlich auch super zeichnen, z.B. die einfache lineare Funktion f(x) = x. Als Laufvariable nehmen wir direkt das x, das von 0 bis 90 in Zehnerschritten läuft. Nur zur Verständlichkeit führen eine lokale Variable y ein.

for (int x = 0; x < 100; x = x + 10) {
  int y = x;
  ellipse(x, y, 5, 5);
}

Die Funktion "steht Kopf", weil die y-Achse ja nach unten zeigt. Wenn wir das richten wollen, müssen wir y invertieren.

for (int x = 0; x < 100; x = x + 10) {
  int y = 100 - x;
  ellipse(x, y, 5, 5);
}

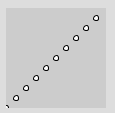
Jetzt können wir auch andere Funktionen zeichnen, zum Beispiel die Funktion f(x) = x / 2 + 50, also eine Gerade mit y-Schnittstelle 50 und Steigung 1/2.

Dazu sollten wir x und y als float wählen, um ganzzahlige Division zu vermeiden. Beachten Sie auch, dass der komplette Term (x/2 + 50) invertiert werden muss.

for (float x = 0; x < 100; x = x + 10) {
  float y = 100 - (x/2 + 50);
  ellipse(x, y, 5, 5);
}

Sinuskurve

Wenn Sie eine Sinuskurve zeichnen möchten, müssen Sie Folgendes bedenken:

1. Die x-Werte für eine Phase der Sinuskurve laufen von 0 bis 2*PI, also ungefähr von 0 bis 6. Sie möchten Ihre Kurve aber über die x-Pixel 0 bis 100 darstellen.
2. Der y-Werte der Sinusfunktion liegen im Bereich von -1 bis +1. Sie möchten aber Punkte auf einem y-Bereich von 0 bis 100 darstellen. Man beachte außerdem, dass die y-Achse des Grafikfensters nach unten zeigt.

Daher muss unser erster (naiver) Versuch scheitern:

size(200,100);
for (float x = 0; x <= width; x += 5) {
  ellipse(x, sin(x), 8, 8);
}

Warum? Erstens werden alle 6 Pixel (x-Wert) eine volle Sinusphase durchlaufen. Zweitens schwanken die Werte von sin(x) zwischen -1 und 1.

Also müssen wir zunächst unseren x-Wert in den Bereich von 0 bis 2*PI bringen. Das machen wir mit der Processing-Funktion map(). Schauen Sie in der Processing-Referenz (unter "Hilfe") nach, wie map() funktioniert.

for (float x = 0; x <= width; x += 5) {
  float x2 = map(x, 0, width, 0, 2*PI);
  // ...
}

Der Wert x2 ist jetzt im Bereich 0 bis 2*PI. Wenn wir jetzt sin(x2) anwenden, müssen wir noch das Ergebnis von [-1, 1] auf [0, 100] abbilden. Um nebenbei noch die Achse umzudrehen, bilden wir von [-1, 1] auf [100, 0] ab.

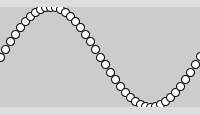
size(200,100);
for (float x = 0; x <= width; x += 5) {
  float x2 = map(x, 0, width, 0, 2*PI);
  float y2 = sin(x2);
  float y = map(y2, -1, 1, height, 0);
  ellipse(x, y, 8, 8);
}

Man kann sich das so vorstellen, dass sich (x2, y2) im Raum der Sinuskurve befindet (x2 in [0, 2*PI] und y2 in [-1,1]) und (x, y) sich im Raum des Grafikfensters (je in [0,100]). Die zweimalige Anwendung von map() transformiert die Werte jeweils von einem in den anderen Raum.

Coding Style

Bitte achten Sie darauf, wo Leerzeichen und Zeilenumbrüche gemacht werden, und wo nicht.

for (int i = 0; i < 3; i++) {
  println(i);
}

Alternativ:

for (int i = 0; i < 3; i++)
{
  println(i);
}

Denken Sie auch daran, Ihre Code mit Bearbeiten > Autoformatierung von Processing korrekt einrücken zu lassen (Tastenkürzel STRG+T bzw. CMD+T).

for (int i = 1; i <= 5; i++) {
  println(i);
}

for (int i = 0; i < 5; i++) {
  println(i+1);
}

Übungsaufgaben

5.2 a) 2er-Schritte   Level 11 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Schreiben Sie eine For-Schleife, die eine Variable zaehler in 2er-Schritten von 0 bis 10 hochzählt. In jeder Runde geben Sie den Wert auf der Konsole aus.

5.2 b) 2er-Schritte rückwärts   Level 11 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Schreiben Sie eine For-Schleife, die eine Variable zaehler in 2er-Schritten von 10 bis 0 runterzählt. In jeder Runde geben Sie den Wert auf der Konsole aus.

5.2 c) Hash-Zeichen   Level 11 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Schreiben sie eine For-Schleife, die eine vorgegebene Anzahl von #-Zeichen (engl. hash) auf der Konsole ausgibt.

int anzahl = 3;

// jetzt Ihr Code...

Auf der Konsole sollte nach Start dies stehen:

###

5.2 d) ASCII-Art 1   Level 21 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Schreiben sie eine For-Schleife, die eine vorgegebene Anzahl von Zeichen ausgibt, dabei sollen # (Hash) und . (Punkt) im Wechsel gedruckt werden. In jedem Schleifendurchlauf darf nur ein Zeichen ausgegeben werden.

int anzahl = 5;

// jetzt Ihr Code...

Verwenden Sie also eine separate Laufvariable, die Sie mit anzahl vergleichen.

Auf der Konsole sollte nach Start dies stehen:

#.#.#

Bei anzahl = 8 entsprechend:

#.#.#.#.

Tipp

Sie müssen Ihre Laufvariable (die könnte i heißen) daraufhin untersuchen, ob sie gerade oder ungerade ist. Dazu verwenden Sie den Modulo-Operator (%).

5.2 e) Streifen   Level 21 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Produzieren Sie horizontale Linien von links nach rechts, die je einen y-Abstand von 10 Pixeln haben.

Hinweis: Arbeiten Sie ohne setup/draw, also im statischen Modus.

5.2 f) Summe   Level 31 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Gegeben sei folgender Code...

int n = 4;

... berechnen Sie die Summe aus 1 + 2 + ... + n. Im Beispiel wäre das 1 + 2 + 3 + 4, also

10

Testen Sie Ihr Programm auch mit anderen Werte, z.B. mit 2 und 5.

Tipp

Sie benötigen eine weitere Variable zum Erfassen der Zwischenergebnisse.

5.2 g) Fakultät   Level 31 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Gegeben sei folgender Code...

int n = 3;

... berechnen Sie die Fakultät von n, also das Ergebniss der Multiplikation von 1 * 2 * ... * n. Im Beispiel wäre das:

6

Testen Sie Ihr Programm auch z.B. mit 5 und 10.

Hinweis: Sie können in Google mit 5! oder 10! das Ergebniss berechnen lassen.

5.2 h) Reihen   Level 31 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Schreiben Sie eine For-Schleife, die auf der Konsole folgendes ausgibt:

  0 0
  1 2
  2 4
  3 6
  4 8

Probieren Sie auch folgende Ausgabe zu produzieren:

  0 4
  1 3
  2 2
  3 1
  4 0

Tipp

Sie haben jeweils zwei Möglichkeiten, die Aufgabe zu lösen. Entweder Sie führen eine neue Variable ein, die auf andere Weise "zählt" als die Laufvariable der For-Schleife oder Sie "berechnen" den zweiten Wert aus der Laufvariable. Versuchen Sie, jeweils beide Lösungen zu finden.

5.2 i) Fibonacci-Zahlen   Level 41 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Verwenden Sie eine For-Schleife, um die ersten 10 Fibonacci-Zahlen zu erzeugen. Die Fibonacci-Zahlen beginnen mit 1 und 1. Jede weitere Zahl ist die Summe der beiden vorangegangenen Zahlen.

Auf Ihrer Konsole sollte erscheinen:

1 1 2 3 5 8 13 21 34 55

Tipp

Definieren Sie zunnächst zwei Variablen, die zu Beginn auf 1 setzen. Diese Variablen sollen während der Schleife immer den letzten und vorletzten Wert enthalten. In der Schleife müssen Sie die Werte entsprechend anpassen. Der Laufparameter der Schleife hat im übrigen nichts mit der Berechnung zu tun.

5.2 j) Parabel   Level 41 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Zeichnen Sie eine Parabel mit Hilfe einer Schleife.

Unter "Funktionsgraphen zeichnen" (s.o.) finden Sie nützliche Hinweise dazu.

5.2 k) Spirale   Level 51 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Zeichnen Sie die folgende Spirale.

Tipp

Zeichnen Sie zunächst einen Kreis (Sie müssen sin/cos bemühen). Versuchen Sie den Kreis mehrfach zu zeichnen, d.h. der Rand wird mehrfach (über)gezeichnet. Dann können Sie sukzessive den Radius verkleinern.

for (INTIALISIERUNG; BEDINGUNG; AKTION)
  ANWEISUNG

for (int i = 0; i < 3; i = i + 1) {
   println("Runde " + i);
}

5.3 Schleifen im aktiven Modus

Wichtig: In Processing benutzen Sie Schleifen normalerweise nicht für Animation. Sie könnten z.B. auf die Idee kommen, einen Ball innerhalb von einer For-Schleife zu animieren:

// (vergeblicher) Versuch einer Animation

int x = 0;

void setup() {
  frameRate(1); // 1x pro Sek. draw() aufrufen
}

void draw() {
  for (int i = 0; i < 100; i++) {
    background(255);
    ellipse(x, 50, 10, 10);
    x++;
  }
  // erst jetzt wird das Werk sichtbar!
}

Hier haben wir die Frame-Rate auf 1 gesetzt, d.h. draw() wird jede Sekunde aufgerufen. Sie sehen für eine Sekunde den Ball in seiner "Endposition" und dannach wird es weiß. Warum? Weil Processing erst am Ende von draw() die Zeichnung sichtbar macht. Alles, was innerhalb von draw() passiert, ist somit unsichtbar, bis die schließende geschweifte Klammer von draw() erreicht ist.

Sie müssen bedenken, dass Sie sich mit dem draw() bereits in einer Art Schleife befinden. Diese draw()-Schleife regelt alles, was mit sichtbaren Veränderungen zu tun hat. Schleifen im aktiven Modus werden daher eher dazu benutzt, um mehrere Schritte innerhalb eines draw()-Aufrufs zu erledigen.

Sie können z.B. drei Rechtecke gleichzeitig malen:

// Drei Rechtecke mit Schleife

int x = 0;

void draw() {
  background(255);

  // zeichne drei Rechtecke, i läuft von 1..3
  for (int i = 1; i <= 3; i++) {
    rect(x, i * 20, 10, 10); // jedes hat andere y-Position
  }

  // passe x-Wert an für Animation
  x++;
}

Schauen Sie sich das unbedingt in einer Tabelle an! Nehmen wir den allerersten Durchlauf von draw(). Jetzt ist x = 0. Wie entwickelt sich i und welcher Code wird in jeder der drei Schleifendurchläufe ausgeführt?

Die drei Befehle der rechten Spalte werden letztlich innerhalb diesen einen (ersten) Durchlaufs von draw() ausgeführt. Das heißt, jedes Mal wenn draw() aufgerufen wird, werden drei Rechtecke gezeichnet, wobei das x jedes Mal ein anderes ist - daher die scheinbare Bewegung nach rechts.

Sie können auch ein einziges Rechteck aus 20 Linien zusammenbauen. Das machen Sie auch mit einer Schleife im draw(). Im jeden Schleifendurchlauf müssen Sie die Linie genau rechts neben die vorige Linie setzen. Dazu benutzen wir die Laufvariable i und addieren sie aufs x drauf.

// fliegendes Rechteck im Eigenbau (Linien)

int x = 0;

void draw() {
  background(255);

  // zeichne "Rechteck" mit Linien
  for (int i = 0; i < 20; i++) {
    line(x + i, 40, x + i, 60);
  }

  // bewege Rechteck
  x++;
}

Da ich die Linien des Rechtecks selbst zeichne, kann ich auch einen Graustufenverlauf herstellen, indem ich mit stroke() die Graustufe jeder Linie festlege. Wieder verwende ich die Laufvariable i - diesmal für die Graustufe.

// Rechteck mit Graustufen

int x = 0;

void draw() {
  background(255);

  // zeichne "Rechteck" mit Linien
  for (int i = 0; i < 20; i++) {
  	stroke(i*10); // lege Graustufe fest
    line(x + i, 40, x + i, 60);
  }

  // bewege Rechteck
  x++;
}

Im aktiven Modus haben Sie es mit einer Schleife in einer Schleife zu tun. Insofern verdeutlichen Sie sich bitte immer wieder, dass die For-Schleife in den obigen Beispielen innerhalb eines einzigen draw()-Aufrufs komplett durchlaufen wird.

5.4 Verschachtelte Schleifen

Eine Tabelle in einer Tabellenkalkulation besteht aus Zeilen und Spalten, die durchnumeriert sind. So kann man jede Zelle über Zeilen- und Spaltennummer ansprechen:

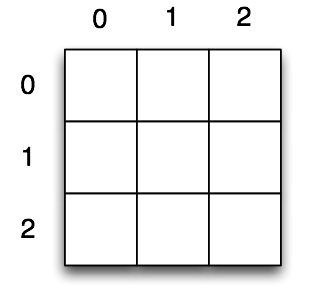
Das gleiche Prinzip finden Sie bei mathematischen Matrizen oder einem Schachbrett wieder. Jetzt kann es sein, dass Sie alle Zellen einer Tabelle oder alle Einträge einer Matrix auf Null (oder einen andere Standardwert) setzen müssen. Dazu müssen Sie also alle Kombinationen von Zeilen- und Spaltennummer durchlaufen.

Sie können sich denken, dass Sie mit einer For-Schleife leicht alle Zeilen durchlaufen können:

for (int z = 0; z < 3; z++) {
  println("Zeile " + z);
}

Zeile 0
Zeile 1
Zeile 2

Genauso leicht können Sie alle Spalten durchlaufen:

for (int s = 0; s < 3; s++) {
  println("Spalte " + s);
}

Spalte 0
Spalte 1
Spalte 2

Jetzt möchten Sie für Zeile 0 alle Spalten 0, 1, 2 durchlaufen, dann für Zeile 1 nochmal und zum Schluss für Zeile 2.

Das erreichen wir, indem wir innerhalb der ersten For-Schleife (Zeilen) die zweite For-Schleife (Spalten) laufen lassen:

for (int z = 0; z < 3; z++) {

  for (int s = 0; s < 3; s++) {
    println("Zeile " + z + ", Spalte " + s);
  }

}

Zeile 0, Spalte 0
Zeile 0, Spalte 1
Zeile 0, Spalte 2
Zeile 1, Spalte 0
Zeile 1, Spalte 1
Zeile 1, Spalte 2
Zeile 2, Spalte 0
Zeile 2, Spalte 1
Zeile 2, Spalte 2

Man spricht hier von zwei verschachtelten For-Schleifen. Dabei ist die Zeilenschleife die äußere Schleife und die Spaltenschleife die innere Schleife.

Man kann die Ausgabe so ändern, dass nur die Spaltennummer der jeweiligen "Zelle" ausgegeben wird (Laufvariable s):

for (int z = 0; z<3; z++) {

  // eine Zeile drucken
  for (int s = 0; s<4; s++) {
    print(s);
  }
  println(); // Umbruch nach fertiger Zeile

}

0123
0123
0123

Alternativ könnten Sie sich die Zeilennummern (Laufvariable z) ansehen:

for (int z = 0; z<3; z++) {
  for (int s = 0; s<4; s++) {
    print(z);
  }
  println();
}

0000
1111
2222

Verschachtelte Schleifen kommen immer dann zum Einsatz, wenn eine zweidimensionale Struktur abgeschritten werden soll, dazu gehören auch Spreadsheet-Tabellen, mathematische Matrizen und Bitmap-Bilder.

Auch im grafischen Bereich kann man 2-dimensionale Strukturen gebrauchen, z.B das folgende Gittermuster:

Wir sehen, dass wir hier systematisch die x-Koordinaten durchlaufen können: 0, 25, 50, 75, 100. Das gleiche gilt für die y-Koordinaten: 0, 25, 50, 75, 100. Jetzt wollen wir auf jeder Kombination dieser Koordinaten einen Kreis zeichen. Also: zwei verschachtelte For-Schleifen!

for (int x = 0; x <= 100; x = x + 25) {
  for (int y = 0; y <= 100; y = y + 25) {
    ellipse(x, y, 10, 10);
  }
}

Beachten Sie, dass wir hier spaltenweise zeichnen. Erst wird die x-Koordinate auf 0 fixiert und wir durchlaufen y=0, y=25 usw. Dann setzen wir x auf 25 und durchlaufen y=0, y=25 usw.

Natürlich könnten wir auch zeilenweise zeichnen: dazu müsste man y in die äußere Schleife verlagern und x in die innere Schleife.

Übungsaufgaben

5.4 a) Kleines Einmaleins   Level 31 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Schreiben Sie das kleine Einmaleins auf die Konsole. Das soll ungefähr so aussehen:

Die 1er-Reihe:
   1 x 1 ist 1
   1 x 2 ist 2
   1 x 3 ist 3
   1 x 4 ist 4
   1 x 5 ist 5
   1 x 6 ist 6
   1 x 7 ist 7
   1 x 8 ist 8
   1 x 9 ist 9
   1 x 10 ist 10
Die 2er-Reihe:
   2 x 1 ist 2
   2 x 2 ist 4
   2 x 3 ist 6
   2 x 4 ist 8
   2 x 5 ist 10

   (und so weiter...)

Tipp

Zählen Sie in der äußeren Schleife die "Reihe" hoch und in der inneren Schleife den "Multiplikator". Vor der inneren Schleife kündigen Sie die neue Reihe an. In der inneren Schleife gehen Sie nach dem folgenden Schema vor:

reihe x multiplikator

5.4 b) ASCII-Art 1   Level 11 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Verwenden Sie zwei For-Schleifen, um folgendes Muster zu produzieren (3 Zeilen, 5 Spalten).

#####
#####
#####

5.4 c) ASCII-Art 2   Level 21 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Verwenden Sie zwei For-Schleifen, um folgendes Muster zu produzieren. Das Programm sollte so flexibel sein, dass Sie auch Quadrate mit mehr als vier Zeilen/Spalten erzeugen können.

#...
.#..
..#.
...#

Tipp

Als erstes bauen Sie ein Quadrat aus #-Zeichen und überlegen dann, wenn Sie ein # und wann ein . drucken wollen.

Es ist auch hilfreich, den zwei Laufvariablen passende Namen zu geben (wie wäre es mit "zeile" und "spalte").

5.4 d) ASCII-Art 3   Level 31 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Verwenden Sie zwei For-Schleifen, um folgendes Muster zu produzieren. Das Programm sollte so flexibel sein, dass Sie auch Quadrate mit mehr als vier Zeilen/Spalten erzeugen können.

####
.###
..##
...#

5.4 e) ASCII-Art 4   Level 31 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Verwenden Sie zwei For-Schleifen, um folgendes Muster zu produzieren. Das Programm sollte so flexibel sein, dass Sie auch Quadrate mit mehr als vier Zeilen/Spalten erzeugen können.

...#
..##
.###
####

5.4 f) Gitter mit Kopfspalte   Level 31 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Zeichnen Sie folgendes Muster (unter Verwendung zweiter verschachtelter Schleifen):

Vielleicht hilft es, zunächst dieses Muster zu zeichnen, und später die Rechtecke hinzuzufügen.

Tipp

Die Rechtecke haben alle einen festen x-Wert. Zeichnen Sie sie außerhalb der inneren Schleife. Außerdem hilft rectMode(CENTER).

5.4 g) Schachbrett   Level 41 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Zeichnen Sie ein Schachbrett-Muster:

Als Zwischenschritt zeichnen Sie zunächst das Brett ohne Einfärbung.

Tipp

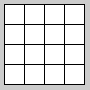
Verwenden Sie Rechtecke und keine Linien, damit Sie später die Felder einfärben können.

Es könnte Ihnen das Leben erleichtern, wenn Sie für die Laufvariablen nicht direkt x und y nehmen, sondern Werte von 0 bis 3, die Sie entsprechend umrechnen.

Tipp

Vielleicht hilft Ihnen die Unterscheidung gerade/ungerade beim Einfärben.

5.4 h) Radial   Level 41 = easy
2 = relativ leicht
3 = mittel
4 = schwierig
5 = hart

Erzeugen Sie folgendes Muster:

Als Zwischenschritt können Sie zunächst das Muster am Ursprung zeichnen und dann "verschieben":

Tipp

Auch hier haben wir es mit einer Art "Gitter" zu tun, nur dass wir uns einerseits im Kreis bewegen (Winkel) und andererseits die Distanz zum Mittelpunkt betrachten. Wie immer bei Kreisen sind Sinus und Cosinus unverzichtbar.

Hier nehmen Sie für Ihre äußere Schleife einen Winkel (z.B. Laufvariable alpha), den Sie in bestimmten Schritten verstellen (bleiben Sie am besten im Bogenmaß). Für jeden Winkel zeichnen Sie Punkte für verschiedene Abstände zum Mittelpunkt (Distanz in Pixeln z.B. Laufvariable d). Mit Hilfe zweier trigonometrischer Formeln können Sie dann x und y ausrechnen: siehe Wikipedia unter "Trigonometrie im rechtwinkligen Dreieck" die ersten zwei Formeln.

for (int z = 0; z<2; z++) {
  for (int s = 0; s<2; s++) {
    println("Zeile " + z + ", Spalte " + s);
  }
}

Zeile 0, Spalte 0
Zeile 0, Spalte 1
Zeile 1, Spalte 0
Zeile 1, Spalte 1