In dem folgenden Projekt wollen wir uns mit der 3D-Welt in Processing vertraut machen und eine Basis für ein First-Person-Spiel legen. In einem First-Person-Spiel sieht man die Spielwelt aus Sicht der Hauptperson. Obwohl dieser Mechanismus mit den "Ego-Shooter"-Spielen bekannt geworden sind (Doom, Quake, Unreal etc.), gibt es natürlich viele andere, wesentlich kreativere Anwendungen für diese Art der Spielsteuerung.

Ziel ist es, dem User eine First-Person-Sicht auf eine 3D-Welt zu geben. Das heißt, er/sie kann z.B. mit den Cursortasten durch diese Welt "fliegen".
Eine Software, die einem solch einen Rahmen an die Hand gibt, nennt man auch Engine (engl. für Motor). Mit Hilfe einer Engine kann man dann eigene Spiele programmieren, ohne jedesmal die Grundprobleme (wie hier die 3D-Steuerung) erneut lösen zu müssen. Eine echte Spiele-Engine enthält natürlich noch viel mehr als das, was wir in diesem Kapitel zusammen entwickeln. Wir konzentrieren uns hier auf die Bewegung im 3D-Raum.
P2.1 Vektoren und die Klasse PVector
Vorab wollen wir unser Wissen bezüglich "Vektoren" auffrischen und die Klasse PVector kennenlernen, die uns im Verlauf dieses Projekts noch helfen wird.
Video: Vektoren und die Klasse PVector (12:48)
P2.2 Planung
Wir planen unsere Software zunächst auf dem Papier und überlegen uns Anforderungen und mögliche Klassen.
Anforderungen
Sammeln wir zunächst mal die Anforderungen und werden für jeden Punkt einen eigenen Meilenstein bauen:
- Darstellung eines "Bodens", damit wir die Bewegung im 3D-Raum sehen
- Steuerung für vorwärts/rückwärts, links/rechts
- Steuerung für Drehung links/rechts
Objektorientierung
Wir konzipieren zwei Klassen: eine Klasse Grid zur Darstellung des Bodens, eine Klasse UserInput für die Steuerung per Tastatur. In diesem Projekt sind Klassen nicht unbedingt notwendig, sie sorgen aber für einen aufgeräumten und übersichtlichen Code. Das ist besonders bei einer Engine wichtig, da der Code allein ja noch keinen Zweck erfüllt, sondern nur die Basis für viele verschiedene Anwendungen darstellt. Objektorientierte Programmierung ist immer dann wichtig, wenn Code später erweitert werden soll.
Wir erinnern uns daran, dass für jede neue Klasse ein neuer Reiter (engl. Tab) in Processing aufgemacht wird. Auf der Festplatte wird für den Reiter eine neue Datei abgelegt.
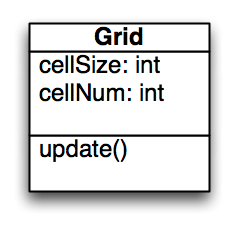
Klasse Grid
Die Klasse Grid soll unseren Boden zeichnen: ein Gitter mit quadratischen Gitterzellen. Welche Eigenschaften soll die Klasse haben? Damit wir den Boden leicht in der Größe anpassen können, wollen wir die Größe als Eigenschaft der Klasse definieren, die dann frei gewählt werden kann. Wie wir später sehen, bietet es sich an, zwei Eigenschaften zu nehmen:
- cellSize: die Größe einer Gitterzelle, d.h. die Seitenlänge einer Zelle in Pixeln (z.B. 40 Pixel)
- cellNum: die Anzahl von Gitterzellen entlang einer Seite des gesamten Bodens, z.B. cellNum = 3, wenn Sie ein 3x3-Gitter haben möchten
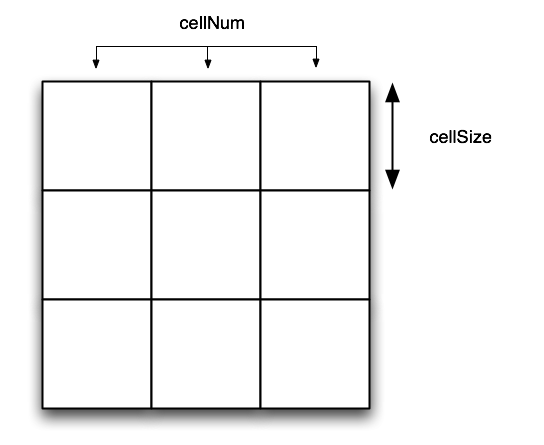
Das Gitter muss in jedem Durchlauf von draw() neu gezeichnet werden. Daher benötigt unsere Klasse eine Methode update(), die immer von draw() aufgerufen wird und dann das Gitter zeichnet.
Im Klassendiagramm sieht Grid also wie folgt aus:
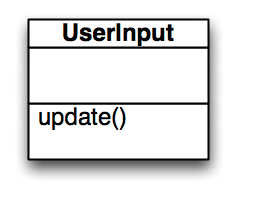
Klasse UserInput
Die Klasse UserInput fragt die Tasten ab und passt unsere "Sicht" an. Um die Tasten regelmäßig abzufragen, muss auch UserInput regelmäßig von draw() aufgerufen werden. Dazu definieren wir auch hier eine Methode update(). Als Klassendiagramm:
P2.3 Darstellung eines Bodens (Klasse Grid)
Als Vorbereitung erstellen wir unseren Sketch mit einer Bildschirmgröße von 600x400 Pixeln und schwarzem Hintergrund:
void setup() {
size(600, 400, P3D); // 3D einschalten!
}
void draw() {
background(0);
}
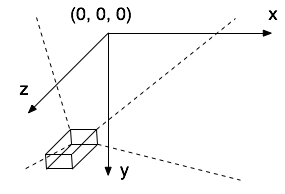
Unsere Klasse Grid soll ein Gitter auf dem Boden zeichnen. Wir erinnern uns an das Koordinatensystem:
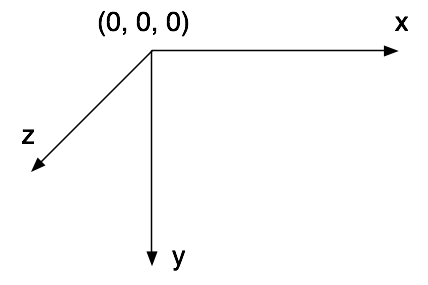
Unser Gitter soll auf der x/z-Ebene liegen, auf der Höhe y = 0, also wie ein Deckel auf dem "Kasten" in obiger Abbildung, allerdings mit (0, 0, 0) genau in der Mitte.
Bevor wir loslegen, müssen wir noch die Kamera-Grundeinstellung anpassen
Kamera-Grundeinstellung
Wie wir den 3D-Raum im Grafikfenster sehen, hängt von der Position und Ausrichtung der "virtuellen Kamera" ab.
Zu beachten ist zunächst, dass in Processing die Kamera-Grundeinstellung derart ist, dass der Nullpunkt (0,0,0) links oben vom Bildschirm liegt. Betrachten wir das Koordinatensystem so, dass wir von der Richtung der x-Achse (also von "rechts", wenn wir die obige Abbildung betrachten) auf das System schauen, dann sieht das so aus (der Kreis mit dem Punkt rechts oben ist die "Pfeilspitze" der x-Achse):
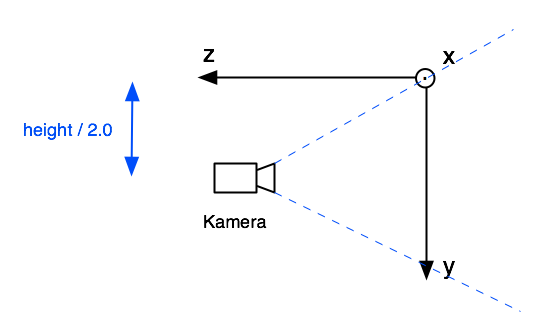
Das sieht man an den Default-Werten der Kamera, wie sie der Processing-Referenz zu entnehmen ist:
camera( // Kameraposition (eye) width/2.0, height/2.0, (height/2.0)/tan(PI*30.0/180.0), // Zielpunkt (center) width/2.0, height/2.0, 0, // Up-Vektor 0, 1, 0 );
Da wir aber wollen, dass (0, 0, 0) genau in der Mitte unseres Boden liegt, müssen wir die Kamera so einstellen, dass wir von oben auf den Nullpunkt schauen. Das heißt, wir verändern Kameraposition (eye) und Zielpunkt (center).
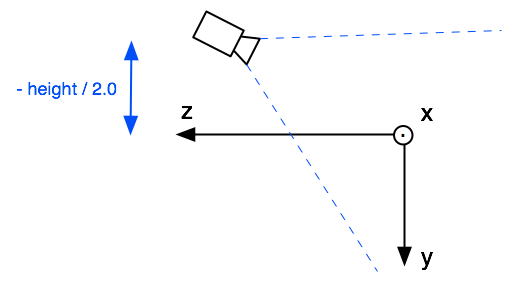
Wir setzen eine Kugel auf den Nullpunkt, um unsere Einstellung zu testen:
void setup() {
size(600, 400, P3D);
grid = new Grid(40, 20);
}
void draw() {
background(0);
// neue Kameraeinstellung
camera(
// Kameraposition, über dem Nullpunkt
0, -height/2.0, (height/2.0)/tan(PI*30.0/180.0),
// Zielpunkt (center) = Ursprung
0, 0, 0,
// Up-Vektor = y-Achse
0, 1, 0
);
sphere(50); // Kugel zum Testen
}
Sie sollten jetzt dies sehen:

Klasse Grid
Jetzt definieren wir unsere Klasse Grid, übergeben die entsprechenden Parameter im Konstruktor und zeichnen erstmal eine Kugel an der Position (0,0,0):
class Grid {
float cellNum = 4;
float cellSize = 20;
// Konstruktor
Grid(float aCellNum, float aCellSize) {
cellNum = aCellNum;
cellSize = aCellSize;
}
void update() {
stroke(200);
sphere(cellSize/2.0);
}
}
Im Hauptprogramm haben wir:
Grid grid;
void setup() {
size(600, 400, P3D);
grid = new Grid(40, 20);
}
void draw() {
background(0);
camera(0, -height/2.0, (height/2.0)/tan(PI*30.0/180.0),
0, 0, 0, 0, 1, 0);
grid.update();
}
Gitter zeichnen
Jetzt zeichnen wir die Gitterlinien. Wir berechnen die Länge der Linien (size) und gehen in einer Schleife durch alle x-Werte.
class Grid {
float cellNum = 4;
float cellSize = 20;
Grid(float aCellNum, float aCellSize) {
cellNum = aCellNum;
cellSize = aCellSize;
}
void update() {
stroke(200);
// Definiere Längen
float size = cellNum * cellSize;
float halfSize = size / 2.0;
// Zeichne Linien entlang der x-Achse
for (int i = 0; i < cellNum+1; i++) {
float x = -halfSize + i * cellSize;
line(x, 0, -halfSize, x, 0, halfSize);
}
}
}
In einer zweiten Schleife machen wir das für die dazu rechtwinkligen Linien entlang der z-Achse.
class Grid {
float cellNum = 4;
float cellSize = 20;
Grid(float aCellNum, float aCellSize) {
cellNum = aCellNum;
cellSize = aCellSize;
}
void update() {
stroke(200);
float size = cellNum * cellSize;
float halfSize = size / 2.0;
// Zeichne Linien entlang der x-Achse
for (int i = 0; i < cellNum+1; i++) {
float x = -halfSize + i * cellSize;
line(x, 0, -halfSize, x, 0, halfSize);
}
// Zeichne Linien entlang der z-Achse
for (int i = 0; i < cellNum+1; i++) {
float z = -halfSize + i * cellSize;
line(-halfSize, 0, z, halfSize, 0, z);
}
}
}
Die beiden Schleifen kann man zusammenfassen, da in beiden Fällen das i genutzt wird:
for (int i = 0; i < cellNum+1; i++) {
float x = -halfSize + i * cellSize;
line(x, 0, -halfSize, x, 0, halfSize);
float z = -halfSize + i * cellSize;
line(-halfSize, 0, z, halfSize, 0, z);
}
Jetzt haben wir ein Gitter als Boden, das wir beliebig in der Größe verändern können und das in jedem draw()-Zyklus neu gezeichnet wird.
P2.4 Steuerung 1: vorwärts/rückwärts/links/rechts
Steuerung bedeutet in unserem Fall, dass wir die Kamera verändern. Möchten wir vorwärts gehen, verschieben wir die Kamera in Richtung negativer z-Achse. Gehen wir rückwärts, verschieben wir entlang der positiven z-Achse. Links und rechts sind Verschiebungen entlang der x-Achse.

Dabei ist zu bedenken, dass wir nicht nur die Kamera verschieben müssen (eyeX, eyeY, eyeZ), sondern auch den Zielpunkt (centerX, centerY, centerZ). Sonst würden wir die Kamera immer auch ein wenig drehen, da sie weiterhin auf den Nullpunkt zeigen würde.
Wir erstellen eine Klasse UserInput, welche die Kamera positioniert und die Tasten-Eingabe verarbeitet. Hier sind bereits alle vier Fälle (vorwärts, rückwärt, links, rechts) behandelt:
class UserInput {
float eyeX, eyeY, eyeZ; // Position Kamera
float centerX, centerY, centerZ; // Zielpunkt der Kamera
float SPEED = 5; // Fortbewegung pro Schritt
// Konstruktor
UserInput() {
eyeX = 0;
eyeY = -height/2.0;
eyeZ = (height/2.0)/tan(PI*30.0/180.0);
centerX = 0;
centerY = 0;
centerZ = 0;
}
void update() {
camera(eyeX, eyeY, eyeZ,
centerX, centerY, centerZ,
0, 1, 0);
if (keyPressed) {
if (keyCode == UP) {
eyeZ -= SPEED;
centerZ -= SPEED;
}
if (keyCode == DOWN) {
eyeZ += SPEED;
centerZ += SPEED;
}
if (keyCode == LEFT) {
eyeX -= SPEED;
centerX -= SPEED;
}
if (keyCode == RIGHT) {
eyeX += SPEED;
centerX += SPEED;
}
}
}
}
Im Hauptprogramm erstellen wir eine Instanz von UserInput und rufen auf dieser Instanz regelmäßig update() auf. Wie Sie sehen, ist das Hauptprogramm sehr aufgeräumt:
Grid grid;
UserInput userInput;
void setup() {
size(600, 400, P3D);
grid = new Grid(40, 20);
userInput = new UserInput();
}
void draw() {
background(0);
grid.update();
userInput.update();
}
P2.5 Steuerung 2: Drehung
Bei einer Drehung bleibt die Position der Kamera gleich (eyeX, eyeY, eyeZ), aber der Zielpunkt (centerX, centerY, centerZ) verändert sich. Zu beachten ist außerdem, dass sich nach einer Drehung auch die Richtungen vorwärts/rückwärts sowie rechts/links ändern - Sie können nicht mehr so komfortabel entlang der Hauptachsen wandern. Aber dazu kommen wir später.
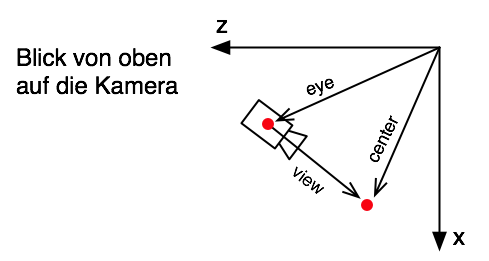
Zunächst mal definieren wir den Vektor, der in die Richtung zeigt, in die die Kamera zeigt. Wir nennen ihn viewVector (in der Abbildung unten: view). Mahtematisch handelt sich um die Differenz (centerX, centerY, centerZ) - (eyeX, eyeY, eyeZ). Wir verwenden im Folgenden die Klasse PVector (für "Processing Vector"), um mit Vektoren zu rechnen.
Eine entsprechende Funktion, die den viewVector berechnet und zurückgibt, definieren wir in der Klasse UserInput:
// Liefert die Richtung, in die die Kamera zeigt,
// als Vektor zurück
PVector getViewVector() {
PVector e = new PVector(eyeX, eyeY, eyeZ);
PVector v = new PVector(centerX, centerY, centerZ);
v.sub(e);
return v;
}
Eine Drehung kann folgendermaßen realisiert werden: Man dreht den viewVector um den gewünschten Winkel und erhält Vektor view2.
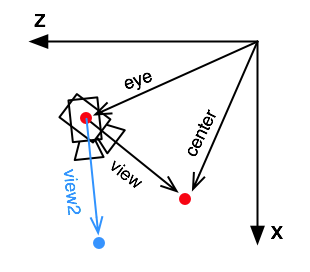
findet dann den neuen Zielpunkt, indem man den gedrehten Vektor view2 auf die Kameraposition eye addiert.
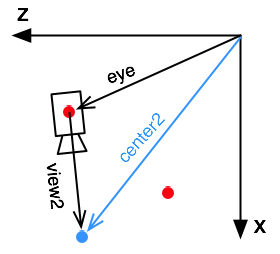
Die Drehung berechnen wir mit der eingebauten rotate()-Funktion der Klasse PVector. Dieses rotate() funktioniert nur im 2-Dimensionalen. Da der viewVector aber immer in der x/z-Ebene liegt, können wir diese Methode dennoch verwenden. Dazu erstellen wir einen temporären Vektor v2, der als y-Koordinate die z-Koordinate des originalen viewVectors bekommt.
// Dreht die Kamera um den gegebenen Winkel
void rotateView(float angle) {
PVector v = getViewVector();
// Funktion rotate() geht nur mit 2D-Vektoren
// daher ein temporärer 2D-Vektor zum Rotieren
PVector v2 = new PVector(v.x, v.z);
v2.rotate(-angle);
// neuer Zielpunkt ist gleich
// Kameraposition + gedrehter viewVector
centerX = eyeX + v2.x;
centerZ = eyeZ + v2.y;
}
Überarbeitung von vorwärts/rückwärts
Was bedeutet es jetzt, vorwärts zu gehen? Wir können leider nicht mehr einfach die z-Achse allein betrachten. Wir möchten uns in die Richtung des viewVectors bewegen. Dazu normalisieren wir ihn (d.h. bringen ihn auf Länge 1) und multiplizieren ihn dann mit unserer Schrittgröße (SPEED). Wir verwenden hier wieder PVector und seine Methoden normalize() und mult():
void moveForward() {
PVector v = getViewVector();
v.normalize();
v.mult(SPEED);
eyeX += v.x;
eyeZ += v.z;
centerX += v.x;
centerZ += v.z;
}
Überarbeitung von links/rechts
Auch das links/rechts verändert seine Bedeutung. Wir verwenden wieder den viewVector als Basis und verändern diesen, um ihn später auf die Kameraposition und -zielpunkt aufzuaddieren. Hier verwenden wir die Drehungsfunktion rotate(), um den Vektor 90° nach rechts (halbes Pi im Bogenmaß) bzw. nach links (270° oder anderthalb Pi) zu drehen.
void moveSideways(boolean toRight) {
PVector v = getViewVector();
// um 90 Grad drehen
PVector v2 = new PVector();
v2.x = v.x;
v2.y = v.z;
if (toRight) {
v2.rotate(HALF_PI);
} else {
v2.rotate(PI + HALF_PI);
}
v.x = v2.x;
v.z = v2.y;
// Größe anpassen
v.normalize();
v.mult(SPEED);
eyeX += v.x;
eyeZ += v.z;
centerX += v.x;
centerZ += v.z;
}
Wir haben jetzt eine fertige Navigations-Engine im 3D-Raum und können diesen jetzt mit Spielfiguren, Hindernissen etc. bevölkern.
P2.6 Steuerung 3: Gleichzeitigen Tastendruck verarbeiten
Bei unserer bisherigen Steuerung gibt es ein Problem: Wenn Sie
gleichzeitig nach vorn und nach rechts steuern, wird nur eins
von beiden ausgeführt. Das liegt daran, dass die Variable
keyCode
(und auch
key
) immer die zuletzt
gedrückte Taste speichern und Sie also nicht auf zwei gleichzeitig
gehaltene Tasten adäquat reagieren können.
Die Lösung ist, dass Sie sich selbst merken, welche Taste gerade
gedrückt ist. Für jede Taste, die Sie interessiert, legen Sie
eine boolesche Variable an, die Sie auf
true
setzen,
solange die Taste gedrückt ist. Sobald die Taste losgelassen wird,
wird die Variable auf
false
gesetzt.
Sie benötigen dazu die Funktion keyReleased(). Diese funktioniert wie keyPressed() und wird immer dann von Processing aufgerufen, wenn eine Taste losgelassen wird.
Hier ein Beispielprogramm:
boolean left = false;
void draw() {
println(left);
}
void keyPressed() {
if (keyCode == LEFT) {
left = true;
}
}
void keyReleased() {
if (keyCode == LEFT) {
left = false;
}
}
Hier wird 60 Mal pro Sekunde false geprintet. Sobald Sie die linke Cursortaste drücken, wird true ausgegeben.
Ein ein vollständiges Programm, in dem Sie einen Ball mit den Cursortasten steuern können. Insbesondere können Sie diagonal navigieren, indem Sie zwei Tasten gleichzeitig gedrückt halten
// Gleichzeitiges Drücken wird registriert
int x, y;
boolean hoch, runter, links, rechts;
void setup() {
size(300, 300);
x = width/2;
y = height/2;
}
void draw() {
background(100);
noStroke();
ellipse(x, y, 40, 40);
if (links) {
x -= 3;
}
if (rechts) {
x += 3;
}
if (hoch) {
y -= 3;
}
if (runter) {
y += 3;
}
}
void keyPressed() {
if (keyCode == LEFT) {
links = true;
}
if (keyCode == RIGHT) {
rechts = true;
}
if (keyCode == UP) {
hoch = true;
}
if (keyCode == DOWN) {
runter = true;
}
}
void keyReleased() {
if (keyCode == LEFT) {
links = false;
}
if (keyCode == RIGHT) {
rechts = false;
}
if (keyCode == UP) {
hoch = false;
}
if (keyCode == DOWN) {
runter = false;
}
}
Interaktives Fenster (muss angeklickt werden; dann mit den Cursortasten den Ball steuern):
Mit diesen Hinweisen schaffen Sie es sicher, die Steuerung Ihres 3D-Programms ähnlich zu "tunen".