11 3D-Grafik

Transformationen in 3D funktionieren prinzipiell genau so wie in 2D, nur dass die Funktionen eine Koordinate mehr haben.

In diesem Kapitel schauen wir uns alle Operationen an und gehen dann darauf ein, wie wir in 3D Formen herstellen.

Das Koordinatensystem erweitert sich mit der z-Achse um die dritte Dimension. Bei Processing zeigt die z-Achse aus dem Bildschirm hinaus auf den Betrachter:

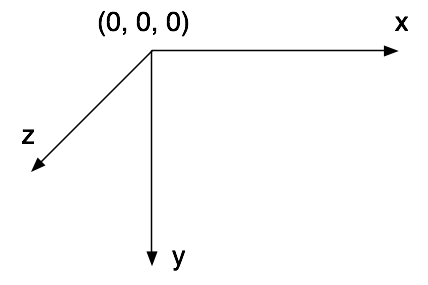
11.1 3D-Formen

Damit wir überhaupt sehen, dass wir uns im 3D-Raum befinden und welche Operationen wir anwenden, erzeugen wir zunächst mal zwei primitive Formen.

3D einschalten

Um in 3D arbeiten zu können, müssen wir Processing sagen, dass es den sog. 3D-Renderer verwenden soll. Das wird als drittes Argument der Funktion size übergeben. Man kann dort P3D oder OPENGL angeben.

size(200,200,P3D); // verwende 3D-Renderer

Quader und Kugel

Die zwei primitiven Grundformen, die uns in 3D zur Verfügung stehen, sind der Quader mit dem Befehl box und die Kugel mit dem Befehl sphere . Das folgende Programm zeichnet einen 3-dimensionalen Quader:

size(200,200,P3D);
box(80,50,30); // Breite, Höhe, Tiefe

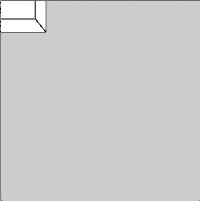
Problem: Der Quader sitzt links oben im Bild. Wir greifen etwas vor und verwenden 3D-Translation, um den Quader in die Bildmitte zu rücken.

size(200,200,P3D);
translate(100,100,0); // schiebe Quader in Bildmitte
box(80,50,30);

Das gleiche für eine Kugel. Beachten Sie, dass Sie den Radius angeben und nicht den Durchmesser wie bei ellipse.

size(200,200,P3D);
translate(100,100,0);
sphere(50); // Kugel mit Radius 50

Wenn Sie die Kugel um 50 Pixel auf den Betrachter zubewegen, dann müssen Sie das mit einem positiven z-Wert in translate machen:

size(200,200,P3D);
translate(100,100,50);
sphere(50);

Drahtgitter / Licht

Wie Sie sehen, besteht die Kugel aus lauter kleineren Flächen, nämlichen Dreiecken. Die Ränder der Dreiecke ergeben ein sog. Drahtgittermodell (engl. wire frame mesh oder einfach nur mesh). In Processing wird das Mesh mit dem Stroke gezeichnet und die Zwischenräume mit fill gefüllt. Wenn man also das Drahtgitter nicht sehen möchte, schreibt man noStroke(). Jetzt hat man jedoch nur eine weiße, scheinbar zweidimensionale Fläche. Um diese plastisch zu machen, fügt man Lichter hinzu:

size(200,200,P3D);
noStroke(); // kein Drahtgitter
lights(); // Standard-Beleuchtung hinzufügen
translate(100,100,50);
sphere(50);

Die Beleuchtung kann man sehr genau kontrollieren (wie viele Lichter, welcher Typ, welche Richtung/Intensität), aber das machen wir an anderer Stelle.

11.2 Kamera

Damit Sie den 3D-Raum überhaupt betrachten können, muss eine virtuelle Kamera in diesem Raum plaziert werden, damit klar ist, welchen Ausschnitt Sie sehen möchten.

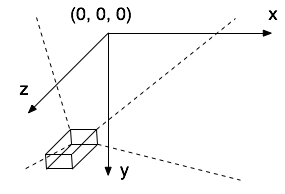
Der Befehl camera setzt Ihre virtuelle Kamera:

camera(eyeX, eyeY, eyeZ,
       centerX, centerY, centerZ,
       upX, upY, upZ);

Die Parameter bestimmen die Position der Kamera im Raum (eye), die Ausrichtung mittels eines Punkts, auf den die Kamera zeigt (center) und einen Vektor, der anzeigt, wo "oben" ist (up).

Die normale Position der Kamera sehen Sie im folgenden Code. Sie können diese dann modifizieren:

size(200,200,OPENGL);

camera(width/2.0, height/2.0, (height/2.0)/tan(PI*30.0/180.0),
    width/2.0, height/2.0, 0,
    0, 1, 0); 

translate(100,100,0);
box(80,50,30); // Breite, Höhe, Tiefe

Binden Sie z.B. die Kameraposition (eye) an die Mausposition, um ein wenig "um die Ecke" zu schauen:

void setup() {
  size(200, 200, OPENGL);
}

void draw() {
  background(100);

  float eyeX = mouseX;
  float eyeY = mouseY;

  camera(eyeX, eyeY, (height/2.0) / tan(PI*30.0 / 180.0),
  width/2.0, height/2.0, 0,
  0, 1, 0);

  translate(100, 100, 0);
  box(80, 50, 30);
}

Interaktives Feld:(Ihre Mausposition bestimmt die Kameraposition)

Brennweite

Neben Position und Ausrichtung der Kamera können Sie auch die "Brennweite" des Objektivs bestimmen. Technisch regelt man die Brennweite in Processing über den Winkel des Erfassungsbereichs der Kamera. Die Brennweite bestimmt, wie zwei Objekte im Verhältnis zueinander dargestellt werden. Bei Tele-Brennweiten (enger Winkel) sind zwei Objekte relativ "naturgetreu" zueinander dargestellt, wohingegen Weitwinkel-Brennweiten (großer Winkel) eine starke Verzerrung mit sich bringen, d.h. nähere Objekte wirken überproportional viel größer als weiter entfernte.

Zum Einstellen benutzen wir den Befehl perspective .

perspective(fovy, aspect, zNear, zFar)

Interessant ist fovy, das bedeutet "field of view", wird im Bogenmaß (radians) gemessen, und ist standardmäßig auf 60° eingestellt.

Hier ein Stück Code mit den Standardwerten. Sie können über die Cursortasten (hoch/runter) die field-of-view ändern.

float fov = PI/3.0;

void setup() {
  size(200, 200, OPENGL);
  noStroke();
}

void draw() {
  background(100);
  lights();

  float cameraZ = (height/2.0) / tan(fov/2.0);

  perspective(fov, float(width)/float(height),
  cameraZ/10.0, cameraZ*10.0);

  float eyeX = mouseX;
  float eyeY = mouseY;

  camera(eyeX, eyeY, (height/2.0) / tan(PI*30.0 / 180.0),
  width/2.0, height/2.0, 0,
  0, 1, 0);

  translate(40, 100, 0);
  box(30, 30, 30);

  translate(70, 0, 100);
  box(30, 30, 30);

}

void keyPressed() {
  if (keyCode == UP) {
    fov += .05;
    println(degrees(fov));
  }
  if (keyCode == DOWN) {
    fov -= .05;
    println(degrees(fov));
  }
}

11.3 Transformationen

Translation

Funktioniert wie im 2D-Raum, nur mit drei Parametern:

translate(x, y, z)

Rotation

Bei der Rotation unterscheidet man zwischen den drei Rotationen um die Hauptachsen, also x-, y- und z-Achse. Daher gibt es drei Befehle:

rotateX(angle)
rotateY(angle)
rotateZ(angle)

Wobei angle im Bogenmaß angegeben wird. Die Drehung wird gegen den Uhrzeigersinn vorgenommen, wenn man vom Ursprung in die Richtung der jeweiligen Hauptachse schaut.

Skalierung

Skalierung funktioniert auch wie in 2D. Entweder mit einem Parameter, der in alle Richtungen gleich skaliert, oder mit drei Parametern für die drei Hauptrichtungen:

scale(s)
scale(x, y, z)

Transformationsmatrix

Genau wie in 2D können Sie mit pushMatrix und popMatrix die aktuelle Transformation speichern bzw. verwerfen.

11.4 Komplexe Formen

Komplexe Formen, jenseits von Quadern und Kugeln, lassen Sie mit den Befehlen beginShape und endShape herstellen. Sie spezifizieren hier ein Objekt über Zwischenpunkt mit vertex .

Hier eine zweidimensionale Figur (Quadrat) mit geschlossener Fläche (Stichwort CLOSE ):

float angle = 0;

void setup() {
  size(130, 130, OPENGL);
}

void draw() {
  background(100);

  translate(60, 40, 0);
  rotateY(angle);
  angle += .01;

  beginShape();
  vertex(0, 0, 0);
  vertex(50, 0, 0);
  vertex(50, 50, 0);
  vertex(0, 50, 0);
  endShape(CLOSE);
}

Sie können mit dem Stichwort TRIANGLES auch eine Reihe von Dreiecken produzieren:

float angle = 0;

void setup() {
  size(130, 130, OPENGL);
}

void draw() {
  background(100);

  translate(60, 40, 0);
  rotateY(angle);
  angle += .01;

  beginShape(TRIANGLES);
  vertex(0, 40, 0);
  vertex(40, 40, 0);
  vertex(20, 0, -20);

  vertex(0, 40, 0);
  vertex(20, 40, -40);
  vertex(20, 0, -20);

  vertex(40, 40, 0);
  vertex(20, 40, -40);
  vertex(20, 0, -20);
  endShape();
}